All published articles of this journal are available on ScienceDirect.
A New Simple Design Method for the Plate Foundation of a Transmission Tower in Subsidence Area
Abstract
In this article, we present a simple design method for the plate foundation of a transmission tower in a mining area, which is based on the theory of beam rested on an elastic foundation. The corresponding theoretical model has been developed with the synergistic reaction of a composite protection plate by considering the mining subsidence of ground. On the basis of this model, the function of flexural deformation and the distribution function of bending moment of the protection plate and their corresponding base counterforce have been deduced. The analysis of selected example shows that the control bending moment of the protection plate is the maximum positive bending moment at the center of the cross section during the moving process of pelvic floor. The tilt deformation is minimum, when the tower is either at the bottom or at the verge of pelvic floor. The tilt deformation is maximum at one-fourth times of the length of pelvic floor and is away from the bottom and the verge of pelvic floor. The contact pressure between the plate foundation and the soil is similar to a U-shaped distribution, when the protection plate is in pelvic floor area of a positive (curvature) deformation, and it is a M-shaped distribution, when the protection plate is in pelvic floor area of a negative (curvature) deformation. We do not observe any change of the contact pressure at the midpoint of the protection plate during the moving process of the basin.
1. INTRODUCTION
Since long, the surface deformation caused by the coal mining had led a great influence often damages to the transmission line in the major coal regions of China, i.e., the Shanxi Province. It has increasingly become a major social problem by virtue of disruption in the power transmission lines and hence threatening the grid security and the local economic development [1]. In recent years, new transmission lines are being added in the provincial grid in the mining areas including 1,000 kV lines, e.g., Jingdongnan-Nanyang-Jingmen Transmission Line, which is the first UHV transmission line in China. As a consequence, such transmission line might be affected by the ground deformation and the displacement. Therefore, it is pertinent to study the mechanism and the design methods of various techniques of anti-deformation and their adopted measures including the composite plate foundation, as these have been shown in Figs. (1-3), which ensure the safe operation of transmission lines.
The plate foundation of a transmission tower is a new type of anti-deformation foundation, which has been used to protect the transmission lines in the mining areas, as it has widely been proposed by the contractors and researchers in recent years. The engineering practice shows that it can effectively reduce the changes of tower’s foot distance and uneven settlement of supports caused by underground coal mining. In other words, it can significantly reduce the influence and damage to the upper structure of the tower by the surface deformation [2-4].
Hence, it has widely been used in the transmission lines, which are located in those coal mining areas.
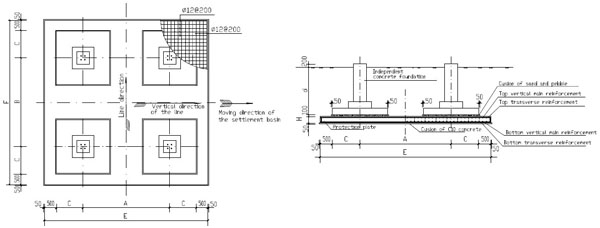
A schematic diagram of a typical composite plate foundation along with the protection plate.

The details of construction for a concrete plate.
Owing to the variations of the surface deformation and the complexity of the mechanism of the transmission tower, only a few publications have provided the numerical analysis and the experiments-based simulations by considering the deformation mechanism of the composite plate foundation for the transmission towers located in the mining areas; whereas, the mechanism and the design of the plate foundation are not explored yet. T. Liu [5] has conducted the qualitative analysis to assess the principle behind the composite plate foundation. Q. J. Shu [6] has discussed the appropriate thickness of the protection plate by using the numerical analysis of a typical transmission line as well as its foundation. X. Y. Zhang [7] has preliminary verified the effect of resistance to the deformation of composite plate foundation by using the modeling techniques at laboratory scale. Through a qualitative analysis, Q. Z. Qin [8] has suggested a reinforced design of the composite plate foundation of a transmission tower in the mining areas. Her analysis concluded the absence of theoretical basis, where internal force is controlled by separating it from the actual situation. Hence, it is not possible to guide this proposed design in the engineering applications. This study can only be viewed as a typical engineering problem rather than any theoretical development involving the mechanical mechanism of the composite plate foundation and the existing protection plate that may be dominated by an empirical design. It brought hidden trouble to the safety of existing and new transmission lines. To ensure the safety of the transmission line, we further developed the theoretical background of the mechanism involved in the designing of the composite plate foundation by considering the surface deformation affect.

The details of construction of an independent foundation.
Currently, there are many difficulties for assuming the composite plate foundation of a transmission tower as a kind of free boundary sheet for a settlement foundation during the stress analysis. For the case of stress analysis of a sheet, which is rested on an elastic foundation in areas without mines, the researchers have often used the superposition method, the calculus of variations, Fourier transform method, etc. For the case of four-edges-free plate on an elastic foundation subjected to a concentrated load at the center, F.F. Zhang [9] have developed a superposition method where the original mechanical state of the sheet can be decomposed into five different boundary conditions. Y. Huang [10] has obtained the exact solutions of the rectangular plates with free edges by using the trigonometric series of superposition. X.F. Lian [11] and Q. Z. Qu [12] have adopted the method of Fourier double transformation and have obtained bending analytic solution of a rectangular plate, with free boundaries at its four corners, which rested on an elastic foundation under the condition of a vertical load. R. Li [13] has presented a new simple method of supervision to solve the problem analytically by invoking Hamilton canonical equations.
The above-described methods are numerically complex and often impossible to get a solution from them. One of the disadvantages of these methods is that the deformation of the ground surface creates the decomposition and superposition stresses on the plate as well as on its boundary conditions. The existing methods are unable to express the deflection function, which cannot only satisfy the boundary conditions for the four edges of free elastic thin plate rested on an elastic foundation but also reflect the interaction between the sheet and the soil foundation in mining areas. Therefore, a more reasonable and simple method is needed for force analysis and design for the composite plate foundation of transmission tower in mining areas.
In recent years, many authors have made significant contributions for the synergy of building foundation in mining areas. Only a few theoretical analyses for the stress of masonry structures and of elastic foundations have been presented by G. Q. Zhou [14], G. Wu [15], K. Z. Deng [16] and Z. X. Tan [17]. Tan’s results [17] are only fit for those foundations under uniformly distributed load. In this article, we used their studies as an immediate useful reference for onward implementation of their work for a simple model of the composite plate foundation for a transmission tower.
This article has developed a simple model of the composite plate foundation for a transmission tower subject to the surface deformation in mining areas. On the basis of the beam theory for an elastic foundation, a theoretical method has been developed by combining the tower's composite plate foundation and the mining-induced elastic ground. Based on this model, the functions of flexural deformation, the distribution functions of sectional moments, and the subgrade reaction of the protection plate have been deduced. It provides the theoretical base for the scientific design of a composite plate foundation for a transmission tower.
2. A SIMPLE MODEL OF COMPOSITE PLATE FOUNDATION OF TRANSMISSION TOWER
2.1. The Prototype of Composite Plate Foundation
In this article, the composite plate foundation is mainly comprised of: (1) the upper four independent concrete foundations, (2) the protection plate at the bottom, and (3) a sliding layer of suitable thickness, which is usually composed of sand and gravel and situated in between the concrete foundations and the protection plate (refer to Figs. 1-3).
2.2. Assumptions
As it has been discussed earlier, the existing methods of elastic thin plate (i.e., four free edges rested on an elastic foundation) are not suitable for the composite plate foundation in mining areas owing to the deformation of the surface-soil complex. Therefore, to calculate the bending moment of a protection plate under the influence of mining subsidence, the plate has been assumed as a beam with a rectangular cross-section, which is rested on an elastic soil, by considering the following assumptions:
- The soil in the mining areas can be considered as a perfect elastic and the reaction is proportional to its compressional deformation.
- Only pressure (no tension) is considered on the contact surface between the soil and the foundation subsidence.
- The plate foundation subsides by having a full contact to the soil, i.e., there is no space between them.
- It has been assumed that the composite plate foundation is always in an elastic state without considering the damages to its foundation.
- It has been assumed that the subsidence basin is moving along the vertical direction of the transmission line by considering the force and the deformation under the linear load.
- As it is almost possible that the surface deformation, the maximum wind load and the ice load are coexisting at the same time, therefore, only the gravity of the tower and its associated lines are considered.
- By considering the sliding layer between the independent foundation and the protection plate, it has been assumed that the vertical pressure (FNV) on the top surface of the plate caused by the tower and its lines is equivalent to load q1 that is uniformly distributed along its longitudinal direction and its distribution length is B (i.e., the width of independent foundation).
After analyzing the moment of the protection plate along the moving direction of the mining basin, the moment of these sections along the vertical direction can be calculated by using the same method.
2.3. A Simple Model of Composite Plate Foundation
It has been assumed that the width of the equivalent beam is one-half times to that of the plate’s transverse size. The simple model of composite plate foundation has been shown in Fig. (4) by considering the gravity only (i.e., the deformation of the ground surface is not considered) for onward simple process of estimation. In this article, we do not consider the protruding parts of structure for a 500 mm long section at its outer end, as it has been shown in Fig. (1).

A simple model of a composite foundation.
The qJC and qKZ can be obtained as follows (refer to Fig. 4):
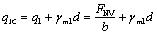 |
(1) |
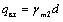 |
(2) |
3. THE INTERACTIVE MODEL OF THE COMPOSITE PLATE FOUNDATION AND THE SUBSIDENCE GROUND
3.1. The Basic Differential Equation
When the subsidence leads to a continuous and limited displacement of the ground surface, the interactive model of the composite plate foundation and the subsidence ground as well as the corresponding coordinate system have been shown in Fig. (5). In Fig. (5), s is the distance between maximum subsidence point and left boundary point of the protecting plate. The length of plate along moving direction of the subsidence area is named as l. The width of the single concrete foundation bottom edge is named b.
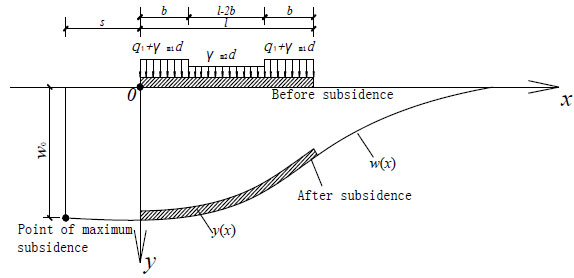
The displacement and deformation of the protection plate just before and after its subsidence.
In Fig. (5), it has been assumed that the origin of the coordinate system is located on the lower left end of the plate. In accordance to the classic theory of an expected subsidence, the subsidence curve of the moving basin after the horizontal seam is fully mined [18-20] and it can be assumed as follows:
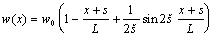 |
(3) |
Here, L is the horizontal distance between the point of maximum subsidence and the boundary point.
In accordance to the load distribution (refer to Fig. 4), the plate has been divided into the three different sections for its solution. The cross-sectional displacement of the plate is such that x∋[0, b], [b, l-b] and [l-b, l] are denoted as y1(x), y2(x) and y3(x) respectively.
In those three sections, the differential equation of the displacement of the plate for an elastic foundation can be expressed as follows (refer to Eqs. (4)-(9)).
(1) For x∈[0, b],
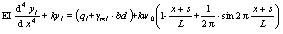 |
(4) |
The general solution of y1 is as follows:
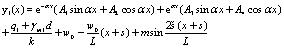 |
(5) |
(2) For x∈[b, l-b],
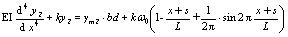 |
(6) |
The general solution for y2 is as follows:
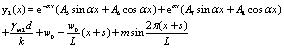 |
(7) |
(3) For x∈[l-b, l],
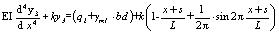 |
(8) |
The general solution for y3 is as follows:
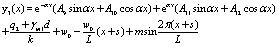 |
(9) |
where,;
3.2. The Solution of the Differential Equation
To get solution of the twelve undetermined constants from A1 to A12 as described in the Eqs. (5), (7) and (9), the following boundary conditions need to be considered.
For x =0, at the left end of the protection plate,
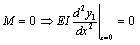 |
(10) |
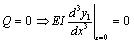 |
(11) |
For x =b, at the inward flange of the left independent foundation,
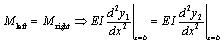 |
(12) |
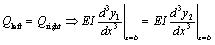 |
(13) |
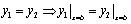 |
(14) |
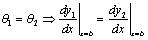 |
(15) |
For x =l-b, at the inward flange of the right independent foundation,
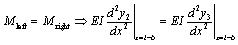 |
(16) |
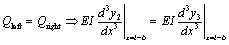 |
(17) |
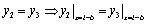 |
(18) |
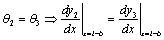 |
(19) |
For x =l, at the right end of the plate,
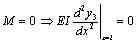 |
(20) |
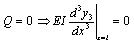 |
(21) |
Thereafter, the following equations can be obtained after substituting the Eqs. (5), (7), and (9) into the Eqs. (10)-(21) of boundary conditions:
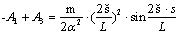 |
(22) |
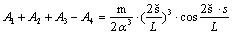 |
(23) |
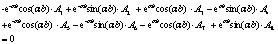 |
(24) |
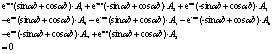 |
(25) |
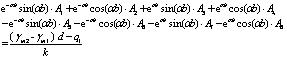 |
(26) |
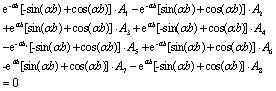 |
(27) |
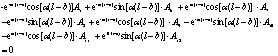 |
(28) |
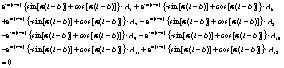 |
(29) |
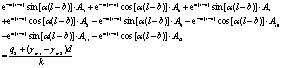 |
(30) |
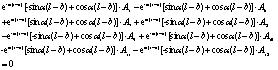 |
(31) |
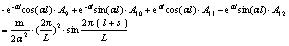 |
(32) |
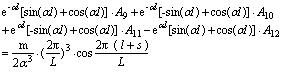 |
(33) |
Next, the solutions of A1-A12 can be obtained by using Eqs. (22)-(33), whereas their expressions are too complex for estimation purposes. Keeping this in view, the specific parameters including α, l, b, m, s, q1, q2, γm1, γm2, d and k may first be substituted into Eqs. (22)-(33), and, thereafter, the method of elimination can be used by either invoking through programming languages (MATLAB) or other numerical analysis software for determining the aforesaid undetermined constants. Next, the expression of deformation of the plate in each section y1(x), y2(x) and y3(x) can be obtained by substituting the undetermined constants into the Eqs. (5), (7) and (9). Finally, the bending moment at the different cross-sectional points and the counterforce at the bottom of the protection plate can be obtained in accordance with Eqs. (34) and (35) respectively.
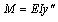 |
(34) |
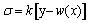 |
(35) |
4. A TYPICAL EXAMPLE AND ITS ANALYSIS
4.1. The Overview
A composite protection plate, of a transmission tower in mining areas, has been chosen to verify the feasibility of the model and its proposed method as described earlier. The maximum settlement of the surface in the area is assumed as: w0 = 2m, the half of the subsidence length of the basin is assumed as: L = 200m, the length of the protection plate of the transmission tower is assumed as: l = 20 m, and the thickness is assumed as: H = 0. m. The side length of the upper independent foundation is approximately taken as: b = 5 m and the embedment depth of the foundation is assumed as: d = 3 m. The equivalent load of the upper tower is considered as: q1 = 5kN/m. The weighted average unit weight of the foundation and the soil is taken as: γm1 = 20kN/m3. The unit weight of the filling soil is γm2 = 17kN/m3. The elastic modulus of base concrete is considered as: E = 2.55×1010Pa. The bedding value is approximately taken as: k = 3×104kN/m3. The values of parameter α, m are 0.3575 and 0.1592, respectively. The major results have been shown as follows:
4.2. The Solution and its Verification
For the purposes of analysis and discussion of the force and deformation conditions of the foundation at different positions in the subsidence areas, the plate has been divided into the three segments along the moving direction of mining subsidence area. Each segment has further subdivided into the four small sections. The arrangement and the serial numbers of the control cross-sections have been shown in Fig. (6). The flexure deformation and the bending moment of the nine control points have been assessed. The distances of the big board from the point of maximum subsidence are 0, L/8, 2L/8, 3L/8, 4L/8, 5L/8, 6L/8, 7L/8 and L. The actual assessment in the case of s=L is the right end of the complex plate and it coincides with the boundary of the subsidence area. The actual assessment in the case of s=0 is the left end of the big plate and it coincides with the maximum subsidence point. Therefore, their corresponding values are 0, 15, 40, 65, 90, 115, 140, 165 and 180 m respectively.

A schematic diagram of the control sections of the protecting plate.
The aforesaid protection plate has been designed and analyzed by the proposed model. The corresponding undetermined constants of different values of s have been obtained (refer to Table 1).
The undetermined constants (A1-A12 [H=0.6m]).
| Parameters | S (m) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 15 | 40 | 65 | 90 | 115 | 140 | 165 | 180 | |
| A1 | -0.000034 | -0.000313 | -0.000619 | -0.000582 | -0.000225 | 0.000244 | 0.000549 | 0.000512 | 0.000326 |
| A2 | 0.000131 | 0.000404 | 0.000677 | 0.000600 | 0.000216 | -0.000248 | -0.000522 | -0.000445 | -0.000239 |
| A3 | -0.000034 | -0.000034 | -0.000034 | -0.000034 | -0.000035 | -0.000035 | -0.000035 | -0.000035 | -0.000035 |
| A4 | 0.000008 | 0.000008 | 0.000008 | 0.000008 | 0.000008 | 0.000008 | 0.000008 | 0.000008 | 0.000008 |
| A5 | 0.001181 | 0.000903 | 0.000597 | 0.000634 | 0.000991 | 0.001460 | 0.001765 | 0.001728 | 0.001542 |
| A6 | -0.000137 | 0.000136 | 0.000410 | 0.000332 | -0.000051 | -0.000516 | -0.000790 | -0.000712 | -0.000507 |
| A7 | -0.000034 | -0.000313 | -0.000619 | -0.000582 | -0.000225 | 0.000244 | 0.000549 | 0.000512 | 0.000326 |
| A8 | 0.000131 | 0.000404 | 0.000677 | 0.000600 | 0.000216 | -0.000248 | -0.000522 | -0.000445 | -0.000239 |
| A9 | -0.000034 | -0.000034 | -0.000034 | -0.000034 | -0.000035 | -0.000035 | -0.000035 | -0.000035 | -0.000035 |
| A10 | 0.000008 | 0.000008 | 0.000008 | 0.000008 | 0.000008 | 0.000008 | 0.000008 | 0.000008 | 0.000008 |
| A11 | 0.001181 | 0.000903 | 0.000597 | 0.000634 | 0.000991 | 0.001460 | 0.001765 | 0.001728 | 0.001542 |
| A12 | -0.000137 | 0.000136 | 0.000410 | 0.000332 | -0.000051 | -0.000516 | -0.000790 | -0.000712 | -0.000507 |
To verify the correctness of the proposed solution, the following result of s at zero is taken as an example. The undetermined constants have been substituted in Eqs. (5), (7) and (9). The functions of the flexure deformation for the protection plate have been obtained, as these have been shown in Eqs. (36)-(38).
 |
(36) |
 |
(37) |
 |
(38) |
Thereafter, by considering the unit width approximately equal to 1 m, the bottom reaction of the base integral sum of a big plate and the resultant force of the bottom reaction of the plate have been obtained by using the integral method for the bottom reaction of the plate (refer to Eq. (39)).
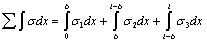 |
(39) |
where, 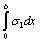 ,
, 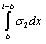 and
and 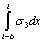 can respectively be estimated by using the Eqs. (40)-(42).
can respectively be estimated by using the Eqs. (40)-(42).
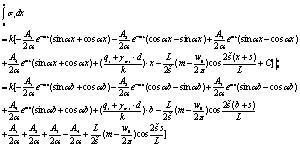 |
(40) |
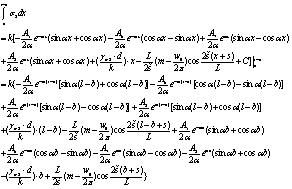 |
(41) |
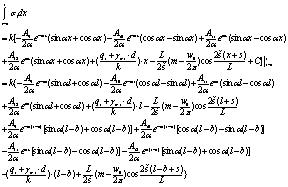 |
(42) |
The sum of the basal reaction can be obtained by using the known parameters including α, l, b, m, s, q1, q2, γm1, γm2, d and k by substituting into Eqs. (40)-(42), as it has been shown in Eq. (43).
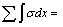 |
(43) |
The resultant force of the upper load at each increment of 1 m width has been shown in Eq. (44).
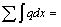 |
(44) |
The ratio between the basal reaction sum and the resultant of the upper load is shown as follows:
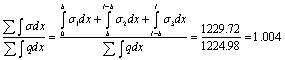 |
(45) |
This shows that the earlier described solution can satisfy the conditions of the static equilibrium, and, the method proposed in this article is accurate and reliable.
4.3. The Displacement and Deformation of the Protection Plate
Fig. (7) shows that the relevant changes in the vertical displacement at each cross-section of the protection plate for different positions in subsidence areas. The different s-values of the plate have been calculated based on the ratio between the difference of the vertical displacement at center of an independent foundation and the horizontal distance (between the center points), as it has been shown in Fig. (8).
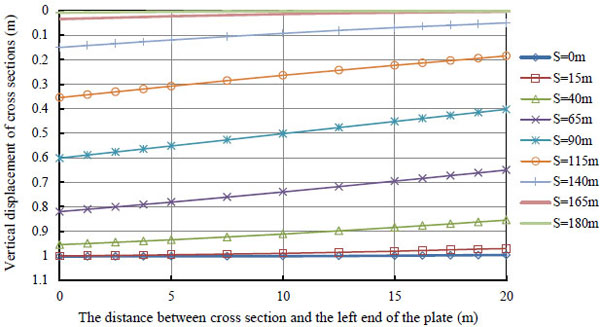
The vertical displacement of a cross-section by considering its different positions.
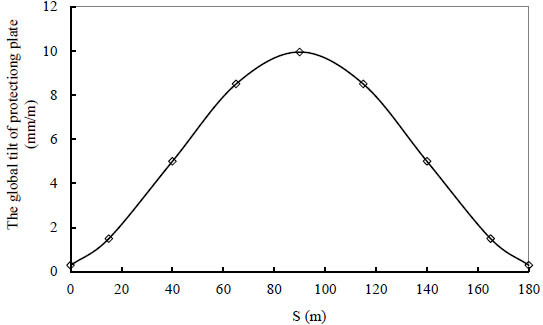
A relation between the global tilt of a protection plate and its position.
Figs. (7 and 8) show that the whole vertical displacement of subsidence for the protection plate has been occurred due to the gravity as well as the interaction between the upper edge of a uniformly distributed load (when located at the bottom of the basin, s = 0 m) and the edge of the basin (s =180 m), where tilting is negligibly small. The ever increasing tilting happens, when the location changes from the bottom of the basin to its position at s=90 m. The slope deformation is large, when s = 90 m. It is consistent with the maximum tilting of the surface that happens at the central position of the basin, i.e., from its edge location towards its bottom.
4.4. Bending Moment of the Protection Plate
Fig. (9) shows that the distribution of the bending moment of the protection plate at each of its cross-section controls it, when it is at different positions of the subsidence basin.
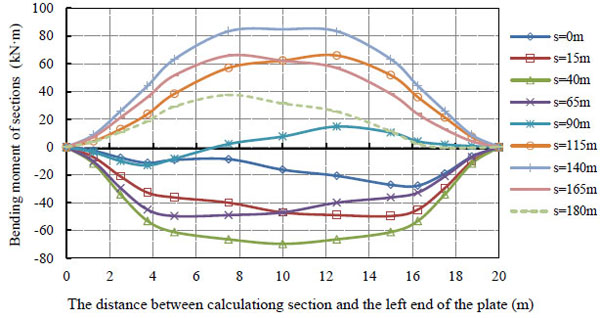
The distribution of a bending moment at control sections.
Fig. (9) shows that the deformation process of the composite plate foundation experiences from the negative curvature to the positive curvature deformation process, in the whole process of the dynamic deformation. The section of the plate in the vicinity of the inside edge of an independent foundation may be taken to be the control section to design in negative curvature phase and the middle section of big plate should be taken to be the control section to design in negative curvature phase. The plate section can be assumed as a control section for the design purposes during the phase of a positive curvature. The designed internal force can be assumed for the worst scenario of a negative curvature phase during the dynamic deformation of the surface. The bending moment of the plate changes between its positive and negative extremes during the deformation of the surface. Hence, the structure of the foundation may be adopted as follows: for its upper and lower edges, the double reinforced layout scheme with a symmetrical reinforced pattern.
4.5. Contact Pressure Between the Plate Foundation and the Soil
Fig. (10) shows the distribution of the contact pressure between the bottom side of the plate foundation and the soil, when s is ranged between 0 and 180 m.
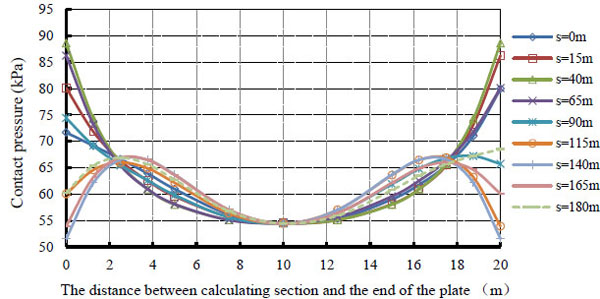
The distribution of a contact pressure between the plate foundation and its corresponding soil.
Fig. (10) further shows that the plate is situated in the curvature area, when s is less than 90 m. The distribution of the contact pressure is similar to a U-shape. The contact pressure at both ends is large, whereas it is minimum at central bottom of the plate. The plate is situated at the largest positive curvature position, when s = 40 m. The maximum contact pressure is 88.6 kN/m2, whereas the minimum contact pressure is 54.4 kN/m2. The distribution of the contact pressure is M-shaped, when s is more than 90 m. The largest pressure is located at the position of an independent foundation and most probably in the central position of an independent foundation. The contact pressure at the end and center of the plate is small. For example, when s=140 m, the maximum pressure is 65.9 kN/m2, whereas the minimum is only 53.9 kN/m2. Fig. (10) also shows the change of contact pressure at the central position of the plate and it is very small and it has nothing to do with s.
CONCLUSION
The following conclusions have been inferred on the basis of this research work:
- On the basis of the theory of the beam that may be rested on an elastic soil, the design theory for the composite plate foundation of a transmission tower in mining areas has been developed. A model by considering the synergy of the composite plate foundation of a transmission tower and the mining-induced elastic ground has been built. The functions of the flexural deformation and the distribution functions of sectional moment have also been deduced, which may provide the theoretical base for the scientific design of the composite plate foundation of a transmission tower and control the deformation of a tower-based structure in subsidence areas.
- The developed model, as described earlier, can be used to estimate the flexure deformation, the cross-sectional bending moment and the base counterforce of the protection plate. The reliability of the model has been verified by using a typical example.
- The analysis of a typical example shows that the control bending moment of a protection plate during the whole process of pelvic floor moving is maximum positive bending moment at the center of the cross section. The slope deformation is minimum at the bottom and at the verge of pelvic floor. The tilt deformation is maximum at one-fourth times of the length of pelvic floor and it is away from the bottom and verge of the pelvic floor. The contact pressure between the foundation and soil is a U-shaped distribution, when the protection plate is in pelvic floor area of a positive (curvature) deformation, and it is a M-shaped distribution in pelvic floor area of a negative (curvature) deformation. We do not observe any change of the contact pressure at the center of the protection plate during the moving process of the basin.
- This article has discussed the feasibility of the estimation model by considering the synergy of the plate foundation of a transmission tower and the mining-induced elastic ground. A collaborative computing model of other cases can also be set up in accordance with the similar method, and, thereafter, these models can be used to conduct their corresponding analysis.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENT
This research was supported by the science & technology projects of China's State Grid Company (Grant No.SGSXYQ00XTJS-(2015)-215), the Fundamental Research Funds for the Central Universities (Grant No.2011QNB18) and the Priority Academic Program Development of Jiangsu Higher Education Institutions. The authors gratefully appreciate this support.


