Study on the System Reliability of Steel-Concrete Composite Beam Cable-stayed Bridge

All published articles of this journal are available on ScienceDirect.

RESEARCH ARTICLE

Study on the System Reliability of Steel-Concrete Composite Beam Cable-stayed Bridge

Buyu Jia Xiaolin Yu, * Open Modal Quansheng Yan Zhen Yang
Authors Info & Affiliations
The Open Civil Engineering Journal • 29 Jul 2016 • RESEARCH ARTICLE • DOI: 10.2174/1874149501609010194

Abstract

Steel-concrete composite beam cable-stayed bridge is a complicated system consisting of a composite beam, tower, and stayed cables. And the composite beam is composed of a steel beam, bridge deck and connectors, which has a different mechanical behavior from the general beam structure. In a word, the steel-concrete composite beam cable-stayed bridge is characterized by specific mechanical behavior and has many influencing factors. Thus, its safety analysis often cannot be easily implemented. This paper aims to study the component reliability of the steel-concrete composite beam based on the stochastic finite element method (SFEM) and the recognition of main failure modes in the system reliability of the cable-stayed bridge. For the component reliability of the steel-concrete composite beam, a nonlinear element model with 10 degrees of freedom (DOF) is adopted, which can consider the particular longitudinal slip effect between the steel and concrete. And the direct differential method (DDM) is used to deduce the response gradient of the element model. Meanwhile, the tower and the composite beam are considered as beam-column members to establish their limit state functions in the form of interaction equations. For the recognition of main failure modes in the system reliability, this paper proposes the concept of uniformity of the reliability index and the refinement strategy to improve the β-unzipping method, which can identify the main failure modes or neglect the unnecessary non-main failure modes. Finally, a certain steel-concrete composite beam cable-stayed bridge is used to verify the effectiveness of the proposed method.

Keywords: Cable-stayed bridge, Direct differentiation method, Interaction equation, Steel-concrete composite beams, Stochastic finite element method, System reliability, β-unzipping method.

1. INTRODUCTION

The reliability problem with only one failure mode is called the component reliability (failure mode and failure component will be considered synonymous throughout this paper). Meanwhile, the reliability problem with various failure modes is called the system reliability. The system reliability is one of the most important and complicated theories of reliability. The system reliability considers the component reliability as the premise. Thus, the numerical computation method of the component reliability that will be adopted is the basis for the system reliability. At present, the numerical computation methods of the component reliability generally include the stochastic finite element method (SFEM), response surface method, and Monte Carlo (MC) stochastic simulation method. SFEM can effectively process the stochastic properties of the related variables involved in structural analysis. After more than 20 years of research, SFEM has made significant progress and is now widely applied in the field of engineering structure. SFEM mainly includes perturbation SFEM [1], Neumann SFEM [2], and structural response gradient method [3, 4]. The most representative SFEM is the direct differential method (DDM) [5]. This method is the one of most accurate and effective methods to calculate the structural response gradient, since its accuracy is considered the same as the structural response. It has been successfully applied in some fields of structural reliability [6-9] in recent years.

The most important problem about the system reliability is related to recognizing the main failure modes. At, present the recognition methods for the main failure modes include load branch bound [12], and β-unzipping [13], increment [10], linear programming [11, 14]. β-unzipping method, which was developed by Thoft-Christensen [13], is the most representative and more widely applied approach. This method uses the reliability index as a control parameter to make the branch-and-bound operation. To avoid combination explosion, a reasonable reliability index β is selected as the bound threshold value at each level of the failure process. The non-main failure model with a small occurrence probability is deleted in advance to effectively improve the computational efficiency. In recent years, various improvement methods based on β-unzipping have emerged, including the revised β-unzipping method by Dong [15] and adaptive dynamic β-unzipping method by Yang [16].

As the computing method for the system reliability developed, the computing theories of the system reliability are used in practical bridges by some scholars. Bruneau [17] analyzed the system reliability of a medium-span cable-stayed bridge. Based on 14 possible plastic failure modes, first-order second-moment method (FOSM) is used to calculate the reliability index. This method is not applicable for a large-span cable-stayed bridge with a higher degree of statistical indeterminacy because it does not consider the influence of geometric nonlinearity and cannot easily and explicitly express the structural response. Imai [6] considered the influence of geometric nonlinearity in successfully analyzing the system reliability in the level 2 of a suspension bridge. The main failure modes are not recognized in the computation. Thus, the final failure series parallel system is huge. Saydam [18] analyzed the system reliability of a suspension bridge using FOSM and focused on the error of extreme distribution random variable against the system reliability based on a simple limit state function (LSF). Gokce [19] utilized detection information to establish a deterministic finite element model using a movable bridge as the objective and calculated the bridge's system reliability, which regards truck position as a random variable. Li [20] started from the equivalent extreme event-based principle under the framework of probability density evolution theory to transform the system reliability problem to a simple reliability problem.

A steel-concrete composite beam cable-stayed bridge is characterized by a large-span, light weight, fine and light appearance, and simple construction. Thus, it has been thoroughly developed over the past decade. However, most research on this bridge type is focused on the deterministic structural analysis, and studies rarely emphasize its reliability (particularly the system reliability) [21-25]. Thus, this paper presents new theories and methods to analyze the component reliability of steel-concrete composite beam and the main failure modes in the system reliability. It also verifies the result of the analysis by considering a composite cable-stayed bridge as the background of engineering. This paper provides a more accurate method for the reliability analysis of composite beam cable-stayed bridge, which could have a role in helping to promote the development of the field of composite bridge safety analysis.

The remainder of this paper is organized as follows: In Chapter 2, the derivation steps of the steel-concrete composite beam element gradient are described based on DDM. Chapter 3 shows the LSFs of the composite beam and tower in the form of an interaction equation. Chapter 4 introduces the concept of reliability index uniformity and refinement strategy and improves the β-unzipping method. The flow chart of the whole algorithm is also given at the end of the chapter. Chapter 5 describes the verification of the proposed method using an actual bridge. The last chapter presents the conclusions.

2. STOCHASTIC FINITE ELEMENT ANALYSIS OF STEEL-CONCRETE COMPOSITE BEAM

2.1. Structural Function Gradient

In finite element analysis, the main structural response, such as the response of internal force or displacement, is first obtained from the control equation. After determining the main response, the element strain or stress can be identified from the main structural response through explicit expression. The main structural response is also the function of the basic random variable. Thus, the performance function g can be written as the function of the main structural response set d = [d1, d2,...dn] and random variable set θ = [θ1, θ2,...θm]:

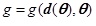(1)

The gradient calculation equation of the performance function g against a certain variable θi (i = 1,.2,...m) is given as

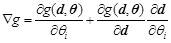(2)

For the nonlinear problem, the equation of the nonlinear structural system can be generally expressed as:

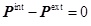(3)

where Pint denotes the internal force of the element, and Pext denotes the external force.

Taking a partial derivative of a certain variable θi on Eq. (3) yields:

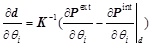(4)

where 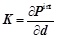denotes the tangent stiffness matrix.

Nataf is used to transform θ from the original space to the independent standard normal space u. Thus,

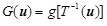(5)

Calculating the gradient vector of the performance function G(u) in the standard normal space yields:

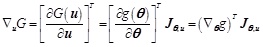(6)

where Jθ, u denotes the Jacobi matrix, and 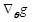is obtained from 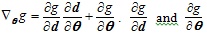can be obtained directly from the performance function. 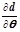can be determined from the vector set of gradient 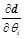of any random parameter θi based on the Eq. (4). Finally, after obtaining 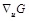, the first-order second-moment method (FOSM) which is combined with the advanced HL-RF iterative method is used to calculate the reliability index β.

Based on Eqs. (2)-(4), it is known that the key of determining the function gradient is to solve 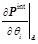. The following paragraph will discuss the solution of 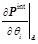in the composite beam element.

2.2. Steel-Concrete Composite Beam Element Gradient

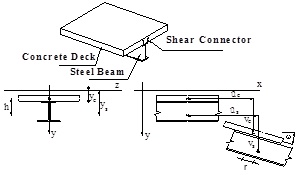
Fig. (1) shows a section of the typical steel-concrete composite beam. The top plate is a concrete bridge deck, and the bottom joist is a steel I-beam. Both plates are connected with shear connectors. The following basic assumptions are adopted:

  1. The cross section is symmetrical to the plane defined by x-y coordinate system
  2. The vertical lift of the composite beam is not considered (vertical deflections of the bridge deck and steel beam are assumed to be consistent).
  3. The influence of shear deformations is disregarded.
  4. The shear connectors are uniformly distributed along the beams.

The vertical deflections of the steel beam and bridge deck can be presented by the same vertical displacement when the vertical lift of the composite beam is not considered. The displacement and the increment of displacement of the bridge deck and steel beam at iteration time t can be presented as

Fig. (1).

Geometric model.

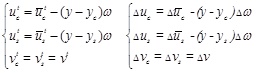(7)

where 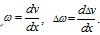subscript S denotes the steel beam, and subscript c denotes the bridge deck. The longitudinal slip displacement and the increment of displacement at t can be presented as:

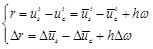(8)

The traditional 8-degree of freedom (DOF) mode (nodes at both sides have 4 DOFs) is not used as the element mode. As for the 8-DOF mode, the interpolation function of u is the first-order polynomial, while the interpolation function of v is third-order polynomial (the interpolation function of v' is second-order polynomial), which will cause slip locking problem. The method of increasing internal DOF can be used to avoid such problem [26]. Therefore, a mode with 10-DOF is adopted herein, in which two DOFs are added to the u displacement inside the element (as shown in Fig. (2). The node displacement and the node increment of displacement at t are given as follows:

Fig. (2).

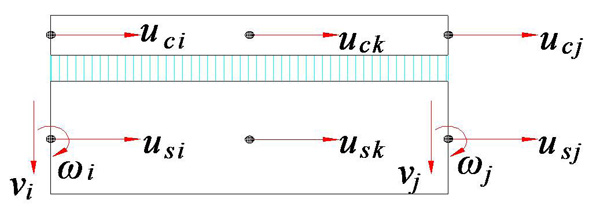
DOF of element.

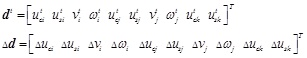(9)

The displacement field of the composite beam is {uc, us, v}, and the displacement and the increment of displacement inside the element at t is presented by the interpolation:

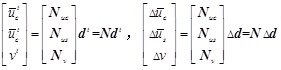(10)

N, Nuc, Nus, Nuc and Nv, are the interpolation functions. The Green strain increment can be presented as:

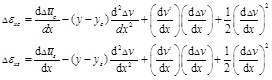(11)

The following equilibrium equation is obtained by combining the principle of virtual work with T. L based incremental method:

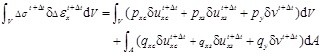(12)

where Pxc and qxc are the corresponding external force and plane force in the x direction acting on the bridge deck, Pxs and qxs are the external force and plane force in the X direction acting on the steel beam, and Py and qy are the external force and plane force in the y direction acting on the composite beam. 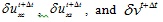are the virtual displacements at 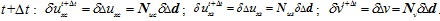. For small strain problems, the relation between the Kirchhoff stress increment and Green strain increment is given as: 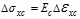for concrete bridge deck, 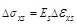for steel beam, and 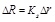for connectors. Finally, element internal force Pint can be obtained as:

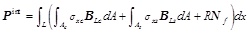(13)

where BLC and BLS are linear expressions of the Green strain increment, BN denotes the nonlinear expression of the Green strain increment, and Bf denotes the slip increment. After computing the partial derivative of a certain variable θi on both sides of Eq. (13), the following equation is finally obtained:

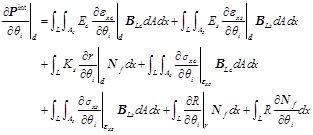(14)

Eq. (14) is the gradient formula of the composite beam in the level of element. If the nonlinear behavior of material is considered, Eq. (14) needs to be further analyzed in the level of the section and the level of the material. It should be noted that different sections and materials will exhibit various gradient formulas [27].

In the following paragraph, the effectiveness of the above-mentioned method is verified by regarding a simply supported composite beam as the objective of the study. Fig. (3) shows a simply supported composite beam which is found in literature [28]. A uniformly distributed load acts on the top member, and a pair of concentrated load, which are equal and opposite, also act on the center of the top and bottom members along the longitudinal direction.

Fig. (3).

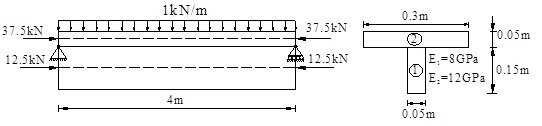
Simply supported composite beam under the action of uniformly distributed load and longitudinal concentration load.

The top and bottom materials are linearly elastic. The elastic modulus of the top member is 12 GPa, and the elastic modulus of the bottom member is 8 GPa. The stiffness of the connectors is presented by a dimensionless stiffness coefficient θL [29]:

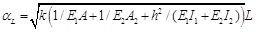(15 )

where L refers to the span length; k denotes the stiffness of the connectors; E1 and E2, A1 and A2, and l1 and l2 denote the elastic modulus, area, and sectional inertia moment of the top and bottom members, respectively; and h denotes the distance between the centroid of the top and bottom members along the height of the cross section.

The area, inertia moment, elastic modulus of the top and bottom members, stiffness of connectors, and uniformly distributed load are selected as random variables. The statistics characteristics of the random variables are shown in Table 1. A1, I1, E1, A2, I2, and E2 of all the elements are assumed to be completely correlated. The performance function is given as:

Table 1.

Statistics characteristics of random variables (A, I, and E refer to the area, inertia moment, and elastic modulus, respectively; Note: [~] in the table means a range of values).

 Structural members  Random variable  Mean  Coefficient of variation  Distribution type
 Bottom member  A1(m2)  7.50×10-3  0.1  Log-normal
 I1(m4)  1.41×10-5  0.05  Log-normal
 E1(MPa)  8.00×109  0.1  Normal
 Top member  A2(m2)  1.50×10-2  0.1  Log-normal
 I2(m4)  3.13×10-6  0.05  Log-normal
 E2(MPa)  1.20×1010  0.1  Normal
 Connector  E3(MPa)  [0.703~1757.81]  0.1  Normal
 Uniformly distributed load  P(kN/m)  1  0.15  Normal
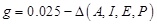(16)

where Δ denotes the vertical displacement of mid-span. Suppose that the stiffness coefficient of the connection is αL = 2 (the corresponding connecting stiffness is k = 2.8215 MPa). By using the proposed method, the following results are obtained: failure probability Pf = 2.2346×10-4 and reliability index β = 3.5107. To verify the correctness of the result, MC method is adopted by sampling 107 times. The results obtained from MC method are: Pf = 2.4662×10-4 and β = 3.4844, which are consistent with the results from the proposed method. The effect of the stiffness of connector on reliability is also analyzed by considering five different stiffness conditions. The result is shown in Table 2. The table indicates that reliability increases dramatically with an increase of the stiffness of connector. However, when the stiffness reaches a certain value, the effect of the stiffness of connector on the reliability becomes insignificant.

Table 2.

Reliabilities under different stiffness of connector.

 Stiffness  Reliability-β  Stiffness  Reliability-β
  αL = 1  0.4488  αL = 4  7.5187
  αL = 1.5  1.8618  αL = 5  7.9696
 αL = 2  3.5107  αL = 8.43  8.2956
  αL = 2.5  5.0608  αL = 10  8.3247
  αL = 3  6.2512   αL = 20  8.3759
  αL = 3.5  7.0406   αL = 50  8.3906

3. ESTABLISHING LIMIT STATE FUNCTION

Based on the Eq (1), the definition of LSF (g = g (d (θ), θ = 0)) of different member in the cable-stayed bridge is discussed in this section. A cable-stayed bridge consists of different members, and the structural forms and forces of these members differ. Thus, their different characteristics should be considered to define the LSF. At present, numerous methods to define the LSF have been developed. However, some methods just considered the failure of stayed cable, and some other methods just considered the failures of beam and stayed cable while neglecting the failure of tower. Beam, stayed cable, and tower are the main components of a cable-stayed bridge, any failure of which has a great affect on the whole structure safety. Thus, these three structural members should be all considered when computing the system reliability.

Theoretically, the bridge system will not collapse immediately when the beam bears the ultimate load, since plastic hinges are at work. However, in the operational stage, the beam is the direct bearing member. If damage occurs in the beam, the traffic will be interrupted. Thus, from a practical perspective, the whole system is considered to be a failure if any beam element is damaged.

Substantial initial tension is exerted on a stayed cable, which produces greater compressive force in the beam and tower. Thus, the beam and tower should be regarded as the beam-column members. The ultimate load of the beam is related to the shape of the cross section, dimensions of all its parts, and loading process. Thus, providing a detailed expression is difficult. However, in engineering applications, the convenient interaction equation can be adopted to calculate the ultimate load, as shown below [30]:

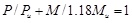(17)

where P and M denote the axial force and the bending moment respectively, Pu denotes the axial force resistance without considering the bending moment, and Mu denotes the bending moment resistance without considering axial force.

Supposing that θ denotes the set of random variables of the bridge, the main structural response is set to be 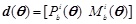. Thus, the LSF of the i-th beam element can be obtained from Eq. (17):

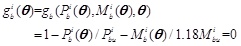(18)

where Pbi (θ) and Pbui denote the axial force and axial force resistance of the i-th beam element respectively, Mbi (θ) and Mbui (θ) denote the bending moment and bending moment resistance of the i-th beam element respectively.

The tower, which is a part that supports the mechanical behavior of the whole bridge, plays an important role in supporting the cable force and the stability of the beam. The occurrence of damage in a tower implies that the balance system of the entire bridge is destroyed. Thus, if the tower is damaged, the whole system will fail. The tower is also a beam-column member. The interaction equation can be the basis for obtaining the LSF of the i-th tower element as follows

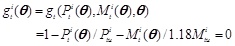(19)

where Pti (θ) and Ptui (θ) denote the axial force and axial force resistance of the i-th tower element respectively, Mti (θ) and Mtui (θ) denote the bending moment and bending moment resistance of the i-th tower element respectively.

The stayed cable differs from the description above. The damage on the stayed cable cannot destroy the whole bridge. Thus, when individual stayed cables are damaged, the whole system is not considered to be a failure. The failure of stayed cable in this paper is considered as a brittle failure. The LSF of the ith stayed cable element is given as

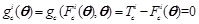(20)

where Fci (θ) and Tci (θ) denote the tensile axial force and tensile axial force resistance of the i-th stayed cable element respectively.

4. SEARCH OF MAIN FAILURE MODE

The calculation is extensive when all failure modes (failure components) are selected. At present the acceptable method is using some particular searching approaches to recognize some main failure modes which have important contributions to the system reliability. Determining how to accurately and effectively recognize the main failure modes is an important problem. This paper proposes the concept of uniformity of the reliability index and the refinement strategy based on literature [16] to improve the β-unzipping method. The improvement is described below.

4.1. Reliability Analysis in Level 1

The system in Level 1 is assumed to be composed of m failure components (e1, e2,...m ). The failure event of component i in Level 1 is presented by Fei(1), and the corresponding reliability index is βei(1). The uniformity of the reliability index in this stage is defined as

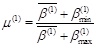(21)

where 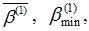and 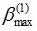denote the average value, minimum value, and maximum value of reliabilities of all the failure components in Level 1, respectively. A smaller uniformity of reliability index indicates that the failure probability in the system is more unevenly distributed. In this situation, few failure components will have higher failure probability. These failure components will likely become candidates for being main failure modes in the level 1. Correspondingly, the initial standard reliability index in the level 1 can be defined as

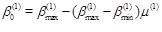(22)

It is supposed that a total of K failure components meet,

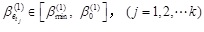(23)

Then the K failure components are selected as the initial candidate failure components in Level 1. Eq. (23) preliminarily gives the selection scope of the candidate failure components. A refinement strategy is also proposed to ensure that the main failure modes are not missing or that unnecessary non-main failure modes are neglected. In other words, the quantity of components is increased (or decreased) based on the K initial candidate failure components from Eq. (23) to observe if system failure probability in Level 1 is changed significantly. First, calculate system failure probability in Level 1 consisting of K candidate failure components (failure system in Level 1 can be considered equal to the series system formed from these candidate failure components events):

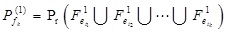(24)

Now λ failure components are added behind the K-th candidate failure components (etk) to increase the number of candidate failure components to be K + λ. The system failure probability Pfk+ λ(1) in Level 1 is calculated based on Eq.(24). If the following condition is met

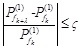(25)

where 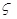denotes a small threshold, then the contributions of the added λ components to system failure probability can be disregarded. Otherwise, if Eq. (25) is not established, the contributions of these λ components to system failure probability should be considered, and these λ components should be selected as new candidate failure components. Similarly, λ failure components are reduced in the front of etk to delete the unnecessary non-main failure modes. Then the number of candidate failure components is reduced to be K + λ, and the corresponding system failure probability Pfk +λ(1) is calculated. Equation (25) will be used again to be the criterion for selecting candidate failure components.

The method above is used to continuously increase or reduce λ until Eq. (25) is met. Finally, the number of candidate failure components in Level 1 can be confirmed to be 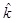, and the corresponding system failure probability is 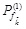. Remarkably, the calculation of 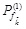will involve the numerical computation method. Whether in a series or parallel system, calculating system failure probability will be finally attributed to the numerical integration of the multidimensional normal distribution. Generally, when the dimension is larger, carrying out the numerical integration of the multidimensional normal distribution is very difficult. This paper adopts the method of equivalent linear safety margin (ELSM) [31].

4.2. Reliability Analysis in Level 2

After 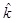candidate failure components are obtained in Level 1, one of the components is selected (it is assumed to be et1 and its corresponding structural element is Et1(1). If Et1(1) undergoes ductile failure, it will be deleted and the virtual load of the element resistance is added at the failure location. If Et1(1) undergoes brittle failure, it will be deleted without any added load. The conditional failure event of failure component S in the remaining m-1 after the failure of et1 is defined as Fes/et1(2). Its reliability index in Level 2 is calculated as βes/et1(2). The reliability indexes of the remaining m-1 88conditional failure events are calculated to confirm the average value βes/et1(2), minimum value βmin/et1(2), and maximum value βmax/et1(2) in Level 2. To define the uniformity of the reliability index and initial standard reliability index in Level 2, the following are computed:

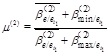(26)
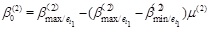(27)

It is supposed that a total of l components (er1, er2,...er1) meet

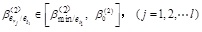(28)

(er1, er2,...er1) are called the initial candidate failure components in Level 2. These candidate failure components are combined with et1 to form a parallel subsystem, namely,

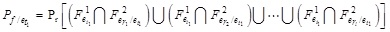(29)

Similarly, 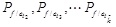can be determined by the same way. Finally, all the parallel subsystems are combined into a big series system to obtain the system failure probability in Level 2.

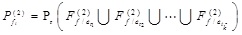(30)

As above, the refinement method is used to add λ failure components behind lth candidate failure component (er1) or delete λ failure components in the front of er1. And continuously increase or reduce the λ until Eq. (25) is met. Finally, the number of candidate failure components in Level 2 is confirmed to be 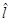, and the corresponding system failure probability in Level 2 is .

Fig. (4).

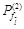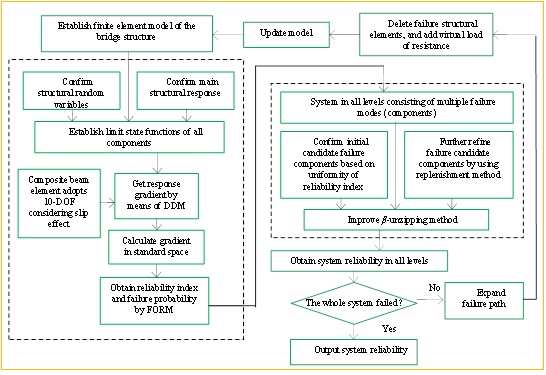
Algorithm flow chart.

4.3. Reliability Analysis in Level 3 or Higher Level

Similar to the method in Level 2, the reliability analysis in Level 3 or higher level can be conducted continuously to expand the failure path until the whole system fails. Calculating system reliability in Level 3 or higher for complicated structures such as large-span bridges will be very substantial. In engineering applications, conducting a system reliability analysis in Level 2 is sufficient. Thus, the analysis of system reliability in this paper only considers the Levels 1 and 2.

Based on the methods and theories described in chapters 2-4, the algorithm flow for the system reliability of the composite beam cable-stayed bridge in this paper is shown in Fig. (4).

5. ANALYSIS ON BRIDGE CASE

A composite beam cable-stayed bridge with a space of (100 + 100) m is considered here. The bridge utilizes double and harp-type cables. The main beam is a steel-concrete composite beam, which is consisted of two steel I-beams, concrete deck and stud connectors. The main beam is rigidly fixed with the towers. The overall layout is shown in Fig. (5).

Fig. (5).

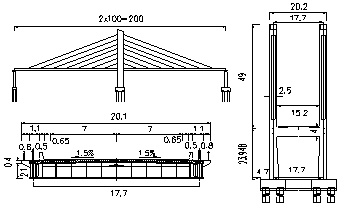
General layout of the bridge (Unit: m).

5.1. Stochastic Finite Element Model

Geometric nonlinearity is considered because of the lower stiffness of the bridge. The statistics characteristics are shown in Table 3. The numbers of finite elements and the corresponding numbers of failure components are shown in Fig. (6). The composite beam is treated as the nonlinear element with 10 DOF as mentioned before, and the tower and cables are treaded normal plane beam element and truss element respectively. Component reliabilities of all elements are calculated by the DDM method.

Table 3.

Statistics characteristics of random variables (Note: [~] in the table means a range of values).

 Random variable  Mean  Coefficient of variation  Distribution type
 bridge deck elastic modulus  Ec(Mpa)  3.45×104  0.1  Normal
 steel beam elastic modulus  Es(Mpa)  2.00×105  0.1  Normal
 up-tower elastic modulus  Etu(Mpa)  3.38×104  0.1  Normal
 down-tower elastic modulus  Etb(Mpa)  3.19×104  0.1  Normal
 cable elastic modulus  Eb(Mpa)  1.95×105  0.1  Normal
 cable single area  Ab(m2)  7.20×10-3  0.05  Log-normal
 composite beam unit weight  ρg(kN/m)  75.8  0.05  Normal
 secondary dead load  Ps(kN/m)  -30.5  0.1  Normal
 composite Beam bending moment resistance  Mbu(kN·m)  [5.18×104~8.34×104]  0.15  Normal
 tower bending moment resistance  Mtu(kN·m)  1.41×105  0.15  Normal
 cable tensile axial force resistance  Tb(kN)  1.20×104  0.15  Normal
 composite Beam axial force resistance  Pbu(kN)  [1.22×105~1.65×105]  0.125  Normal
 tower axial force resistance  Ptu(kN)  3.15×105  0.125  Normal
 stiffness of connectors  Ks(Mpa)  62.1  0.1  Normal
 live load  Pl(kN/m)  -10.5  0.15  Normal

5.2. Effects of Different Forms of LSFs on the Reliability

This paragraph analyzes the reliabilities of the composite beam and tower by considering two forms of LSFs. One doesn't include the effect of axial force on ultimate load, whereas another one includes the effect of axial force on ultimate load by considering the structure as a beam-column member. The two forms are described as follows:

  1. Traditional form: The effect of axial force is not considered. Its LSF can be written as:
  2. (31)
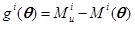
  3. Interaction equation form: The effect of axial force is considered. Its LSF is given in the form of an interaction equation, namely, Eqs. (18)-(19). The comparative result is shown in Fig. (7),
Fig. (6).

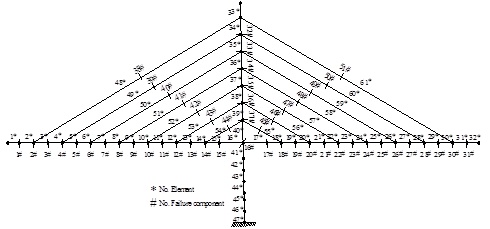
Numbers of finite elements and failure components.

Based on the Fig. (7), the areas of composite beam which have smaller axial forces have the similar reliability results from the two methods, such as the areas of the composite beam corresponded by the 1#–5# and 26#–31# failure components. However, the reliability considering the effect of axial force is significantly smaller than that without considering the effect of axial force in the areas of the composite beam with larger axial force caused by cable force, including the areas of composite beam corresponded by 6#-25# failure components. Likewise, the reliability index is significantly low for the tower because of the effect of axial force. Thus, from a conservative standpoint, the effect of axial force should be considered in calculating the reliability of a cable-stayed bridge.

Fig. (7).

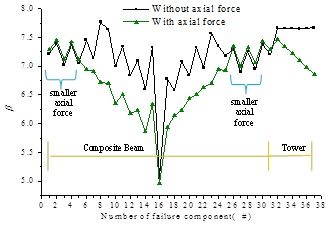
Reliabilities of beam and tower from two LSF forms.

5.3. Calculation and Analysis of System Reliability in the Level 1

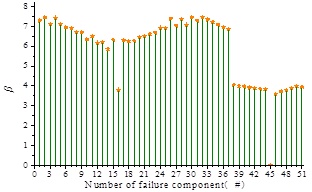
This paragraph calculates and analyzes the system reliability in Level 1. The reliability indexes of all the failure components are shown in Fig. (8) .

Fig. (8).

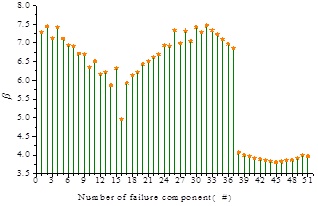
Reliability indexes of all failure components in Level 1.

On the basis of Fig. (8), the minimum reliability index in Level 1 is the reliability index of 45# failure component corresponding to the 55* cable element, namely, βmin1 = 3.80615. The initial standard reliability index is β 0(1) = 4.80065. The initial candidate failure components meeting 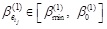are 38#–51# components, corresponding to the 48*–61* cable elements. And the 12#–14# and 16#–19# failure components corresponding to 13*–15* and 17*–20* composite beams are additionally selected by using the refinement method. The candidate failure components are used to form a series system, as shown in Fig. (9).

Fig. (9).

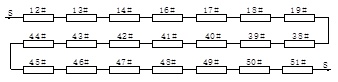
Series system of failure candidate components in Level 1.

The system reliability in Level 1 is obtained by using the method of ELSM: βsystem1 = 3.8762.

5.4. Calculation and Analysis of System Reliability in the Level 2

In the stage of Level 2, the whole bridge system is considered to be failed if any of the 13*–15* and 17*–20* composite beams has been failed. Thus, there are seven corresponding failure components, namely, 12#, 13#, 14#, 16#, 17#, 18#, and 19#. Any failure in 48*–51* cable elements (corresponding to 38#–51# failure components) does not imply the failure of the whole system. These failure components enter into the stage in Level 2, and their failure paths are further expanded. By taking 45# failure component corresponding to 55* cable element as an example, the system reliability after its failure is calculated. The result is presented in Fig. (10).

Fig. (10) indicates that in Level 2, after the failure of 55* cable element, the reliability index of 46# failure component corresponding to 56* cable element has the minimum value, namely, βmin2 = 3.60529. The candidate failure components selected through initial standard reliability index and refinement method include 16# failure component corresponding to 17* composite beam element, and 38#–44# and 46#–51# failure components corresponding to 48*–54* and 56*–61* cable elements. The candidate failure components are combined with 45# failure component in Level 1 to form some sub-parallel systems. These sub-parallel systems are connected to form a series parallel system which is shown in Fig. (11).

Fig. (10).

Reliability indexes of all failure components after the failure of 55* cable element.

Using the similar treatment method after the failure of 55* cable elements, the series parallel systems after the failures of other cable elements can be obtained. Finally, all series parallel systems are connected with seven failure components of the composite beam (12#, 13#, 14#, 16#, 17#, 18#, and 19#) obtained in the stage Level 1 in series to form a hybrid series parallel system, as indicated in Fig. (12).

Fig. (11).

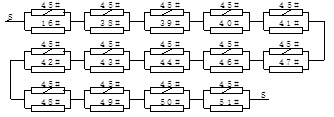
Series parallel system after the failure of 55* cable element.

Finally, after calculation, the system reliability in Level 2 is determined to be βsystem(2). The value is relatively high. That is to say, this composite beam cable-stayed bridge will have higher security assurance and will not easily fail.

Fig. (12).

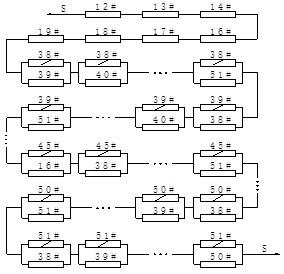
Hybrid series parallel system in Level 2.

CONCLUSION

This paper focuses on the system reliability of a steel-concrete composite beam cable-stayed bridge. The main purpose of this work is to study the component reliability of the steel-concrete composite beam based on the stochastic finite element and recognize the main failure modes in system reliability. The main contributions of the present study can be summarized as follows.

  1. Based on the nonlinear element model with 10 DOF, the DDM of stochastic finite element method is successfully applied to deduce response gradient expression of the steel-concrete composite beam.
  2. The uniformity of the reliability index and standard reliability index is used to initially confirm the scope for selecting candidate failure components. After obtaining the initial candidate failure components, the refinement method is carried out to refine and screen the candidate failure components, and thus identify all the main failure components or neglect the unnecessary non-main failure components.
  3. The axial forces caused by cables are considered in calculating the reliabilities of the beam and tower. The analysis result shows that axial force can cause the reliability index to decrease significantly.
  4. The system reliabilities in Level 1 and Level 2 of a certain steel-concrete composite beam cable-stayed bridge are analyzed by using the above-mentioned method. Finally, the corresponding results are successfully obtained to verify the effectiveness of the method proposed in this paper.

CONFLICT OF INTEREST

The authors confirm that this article content has no conflict of interest.

ACKNOWLEDGEMENTS

The authors disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This paper was supported by the National Natural Science Foundation of China (Nos. 51478193), the Fundamental Research Funds for the Central Universities (Nos. 2015ZM114), and the Open Fund of State Key Laboratory of Bridge Engineering Structural Dynamics (Nos. 201507).

REFERENCES

1 G.B. Beacher, and T.S. Ingra, "Stochastic fem in settlement predictions", J. Geotech. Eng. Div., vol. 107, pp. 449-463, 1981. 2 F. Yamazaki, M. Shinozuka, and G. Dasgupta, "Neumann expansion for stochastic finite element analysis", J. Eng. Mech., vol. 114, pp. 1335-1354, 1988.
[CrossRef Link] 3 P.L. Liu, and A. Der Kiureghian, "Finite element reliability of geometrically nonlinear uncertain structures", J. Eng. Mech., vol. 117, pp. 1806-1825, 1991.
[CrossRef Link] 4 J.P. Conte, P.K. Vijalapura, and M. Meghella, "Consistent finite-element response sensitivity analysis", J. Eng. Mech., vol. 129, pp. 1380-1393, 2003.
[CrossRef Link] 5 M. Barbato, and J.P. Conte, "Finite element response sensitivity analysis: A comparison between force-based and displacement-based frame element models", Comput. Methods Appl. Mech. Eng., vol. 194, pp. 1479-1512, 2005.
[CrossRef Link] 6 K. Imai, and D.M. Frangopol, "System reliability of suspension bridges", Struct. Saf., vol. 24, pp. 219-259, 2002.
[CrossRef Link] 7 M.H. Scott, "Evaluation of force-based frame element response sensitivity formulations", J. of Struc, Eng. (United States), vol. 138, pp. 72-80, 2012.
[CrossRef Link] 8 Q. Gu, and G. Wang, "Direct differentiation method for response sensitivity analysis of a bounding surface plasticity soil model", Soil. Dyn. Earthq. Eng., vol. 49, pp. 135-145, 2013.
[CrossRef Link] 9 Q. Guo, and A.E. Jeffers, "Direct differentiation method for response sensitivity analysis of structures in fire", Eng. Struct., vol. 77, pp. 172-180, 2014.
[CrossRef Link] 10 F. Yuansheng, "Enumerating significant failure modes of a structural system by using criterion methods", Comput. Struc., vol. 30, pp. 1153-1157, 1988. 11 T. Liu, G. Zhao, and G. Zhao, "An effective algorithm for identifying structural dominant failure modes", J. Dalian Univ. Tech., vol. 38, pp. 101-104, 1998. 12 Y.J. Lee, and J. Song, "Risk analysis of fatigue-induced sequential failures by branch-and-bound method employing system reliability bounds", J. Eng. Mech., vol. 137, pp. 807-821, 2012.
[CrossRef Link] 13 P. Thoft-Christensen, "Consequence modified unzipping of plastic structures", Struct. Saf., vol. 7, pp. 191-198, 1990.
[CrossRef Link] 14 M.A. Hadianfard, "Reliability based design optimization of semi-rigid steel frames", In: 11th International Conference on Optimum Design of Structures and Materials in Engineering, OPTI, 2009, pp. 131-142.
[CrossRef Link] 15 D. Cong, "Reliability theory of structural system: advance and review", Eng. Mechan., vol. 79, pp. 88-59, 2001. 16 L. Yang, J. Liu, and B. Yu, "Adaptive dynamic bounding method for reliability analysis of structural system", Tumu Gongcheng Xuebao/China Civil Eng. J., vol. 47, pp. 38-46, 2014. Apr 17 M. Bruneau, Evaluation of system-reliability methods for cable-stayed bridge design, 1992.
[CrossRef Link] 18 D. Saydam, and D.M. Frangopol, "Applicability of simple expressions for bridge system reliability assessment", Comput. Struc., vol. 114-115, pp. 59-71, 2013.
[CrossRef Link] 19 H.B. Gokce, F.N. Catbas, and D.M. Frangopol, "Evaluation of load rating and system reliability of movable bridge", Transp. Res. Rec., no. 12, pp. 114-122, 2011.
[CrossRef Link] 20 J. Li, J.B. Chen, and W.L. Fan, "The equivalent extreme-value event and evaluation of the structural system reliability", Struct. Saf., vol. 29, pp. 112-131, 2007.
[CrossRef Link] 21 A. Zona, M. Barbato, and J.P. Conte, "Finite element response sensitivity analysis of continuous steel-concrete composite girders", Steel Compos. Struct., vol. 6, pp. 183-202, 2006.
[CrossRef Link] 22 J.R. Mujagic, and W.S. Easterling, "Reliability assessment of composite beams", J. Construct. Steel Res., vol. 65, pp. 2111-2128, 2009.
[CrossRef Link] 23 Y. Luo, A. Li, and Z. Kang, "Reliability-based design optimization of adhesive bonded steel-concrete composite beams with probabilistic and non-probabilistic uncertainties", Eng. Struct., vol. 33, pp. 2110-2119, 2011.
[CrossRef Link] 24 H. Cai, and A.J. Aref, "Three-dimensional geometric nonlinear analysis of composite cable-stayed bridges using a refined double-beam model", J. Bridge Eng., vol. 19, p. •, 2014.
[CrossRef Link] 25 X. Deng, and M. Liu, Nonlinear stability analysis of a composite girder cable-stayed bridge with three pylons during construction., vol. Vol. 2015. Mathematical Problems in Engineering, 2015. 26 A. Dall'Asta, and A. Zona, "Slip locking in finite elements for composite beams with deformable shear connection", Finite Elem. Anal. Des., vol. 40, pp. 1907-1930, 2004.
[CrossRef Link] 27 M. Barbato, Finite element response sensitivity probabilistic response and reliability analyses of structural systems with applications to earthquake engineering., Ph.D, Uiversity of California: San Diego, 2007. 28 U. A. Girhammar, and V. K. A. Gopu, Composite beam-columns with interlayer slip - exact analysis, .
[CrossRef Link] 29 U.A. Girhammar, and D. Pan, "Dynamic analysis of composite members with interlayer slip", Int. J. Solids Struct., vol. 30, pp. 797-823, 1993.
[CrossRef Link] 30 W.F. Chen, and T. Atsuta, Beam-Columns Analysis and Design., People's Communication Press: Beijing, 1997. 31 S. Gollwitzer, and R. Rackwitz, "Equivalent components in first-order system reliability", Reliab. Eng., vol. 5, pp. 99-115, 1983.
[CrossRef Link]