All published articles of this journal are available on ScienceDirect.
Experimental Study on Relationship Between Mechanical, Seepage Characteristics and 3D Morphology Parameters of Marble Joint
Abstract
In order to investigate the influence of 3D morphology parameters of marble joint surface on its mechanical and seepage characteristics, artificial joints of coarse-grained marbles were scanned by Tianyuan OKIO-typed 3D laser scanner; and then, the professional software was used to obtain the 3D morphology parameters of marble joint surface. Tests of water flowing through a single joint were conducted under different normal stress and feeding water head by using self-developed radial flowing system, and the exponential function between flow rate per head and normal stress, the linear relation between equivalent hydraulic aperture and mechanical aperture, and the linear relation between joint closure and normal stress were obtained. The relationships between regression parameters in above three formulas and 3D morphology parameters of joint surface were also studied by fitting method. All in all, the results may provide a reference to understand the mechanical and seepage characteristics of rough rock joint.
1. INTRODUCTION
There are a lot of pores and joints in engineering rock mass, the destruction of rock mass is mainly caused by the crack opening and expanding. The deformation and failure of rock mass are controlled by the mechanical and seepage characteristics of rock joint; the morphology of joint surface is the important factor to influence the mechanical and seepage characteristics of rock joint. Therefore, quantitative description of joint surface morphology is one of the key works for studying the seepage-stress coupling mechanism of a rough single rock joint.
In recent years, many scholars have conducted the seepage-stress coupling tests for a single rock joint. Kranz et al., [1] experimentally studied on the permeability of the jointed Barre granites to show that the flow velocity has a power relation with the effective stress. Li and Tao [2] found that there may be a fractal relationship between flow rate per head and normal stress by analyzing the research results of Kranz et al., [1]. Su et al., [3] carried on the seepage-stress coupling test for artificial joint of concrete block and the formula is as follow:
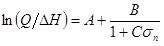 |
(1) |
where A, B and C are the regression parameters, σn is normal stress. Louis [4] found experimentally a negative exponential relationship between hydraulic conductivity and normal stress in a single rock joint. Jones [5] proposed an empirical formula of hydraulic conductivity of carbonate joint as follow:
 |
(2) |
Where p is the normal stress, ph is the normal stress when Kf = 0. Nelson [6] proposed a power equation expressing the relation between permeability coefficient and normal stress for Navajo sandstone joint. Gale [7] put forward a linear equation expressing the relationship between hydraulic conductivity of rock joint Kf and normal stress σn for three kinds of rock joints such as granite, marble and basalt in laboratory. Elliot et al., [8] discovered the linear relationship between the equivalent hydraulic aperture eh and the mechanical aperture em. In the view of Barton et al., [9], mechanical aperture is closed to the equivalent hydraulic aperture in smooth joint surface with a large aperture; the mechanical aperture is several times wider than the equivalent hydraulic aperture for rough rock joint; the hydraulic aperture is approximately linear with the JRC (Joint Roughness Coefficient); however, the nonlinear relationship becomes increasingly remarkable with the increase of JRC, the relationship between equivalent hydraulic aperture bh and mechanical aperture bm based on lots of experiments can be described as follow, which is suitable for bm ≥ bh:
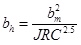 |
(3) |
Witherspoon et al., [10] summarized the linear relationship between equivalent hydraulic aperture bh and mechanical aperture em. Zimmerman and Bodvarsson [11] concluded that the dependence of equivalent hydraulic aperture to the ratio of average mechanical aperture to its standard deviation is less than that of mechanical aperture. Hakami [12] found that the ratios of the average mechanical aperture to hydraulic aperture are 1.1~1.7 for the mechanical aperture of joint with average of 100~500 μm. Sun et al., [13] expressed the normal closure characteristics of rock joint by using an exponential function, While Goodman [14] expressed the normal closure characteristics of rock joint by using a hyperbolic function, which both indicated that the normal closure of rock joint will increase, however aperture of rock joint will decrease gradually with the increase of normal stress.
Above empirical formulas were obtained based on the seepage-stress coupling experiments of the rock joint in the field or in the laboratory, but most of them did not consider quantitatively or qualitatively the influence of joint roughness. Thus, this paper analyzed the relationship between flow rate per head and normal stress, equivalent hydraulic aperture and mechanical aperture, and joint closure and normal stress based on seepage-stress coupling tests for six white coarse-grained marble joints by using self-developed radial flowing system. Additionally, 3D morphology parameters of marble joint surface were used to analyze above three relationships by fitting the relationship between the parameters in above three formulas and some 3D morphology parameters.
2. TEST PROCEDURES
Six white coarse-grained marble samples with grain size of about 5 mm are prepared into standard specimens with the diameter of 50 mm and the height of 100 mm, and then a blind hole with the length of 60 mm and diameter of 6 mm is drilled along the axis of each cylindrical sample. Tensile joints of coarse-grained specimens are made at the midpoint of the long axis by using self-made splitting mold as shown in Fig. (1). The splitting mold is consisted of two same parts, and each part includes an iron plate with a cylindrical groove and an iron wire with triangular section. There is a slot perpendicular to the axial direction in the iron plate at the midpoint of the long axis and the iron wire is fixed in the slot with an edge being used to split the sample.
Joint surfaces of coarse-grained marble specimens are scanned by Tianyuan OKIO-typed 3D laser scanner, in which CCD camera resolution is 1.44 × 106 pixel and the measurement accuracy is up to 20 μm. Because one time of scan is not complete to get all morphology data of the joint surface, mark points (the black rings on the surface, as shown in Fig. (1) are needed to control the splicing of scanning data. For example the scanned upper and lower parts of specimen M1 were processed by Geomagic Studio software as shown in Fig. (2) (Where M1-upper is the upper joint surface and M1-lower is the lower joint surface), in which the yellow circle was generated from the mark points on the surface of the sample. Meanwhile the scanned upper and lower rock joint surfaces of specimen M1 were processed by Geomagic Studio software as shown in Fig. (3). Then 3D morphology parameters of each joint surface are calculated by rock surface morphology test software and the results are as shown in Table 1, in which 3D morphology parameters include Maximum peak height of surface Sp(mm), Maximum valley depth of surface Sm(mm), Contour maximum height Sh(mm), Central line average height Sa(mm), Root mean square height Sq(mm), Skewness Ss, Kurtosis Sk, Contour area ratio SA, Root mean square slope Sdq(mm), The peak average density Sds. Additionally, the average values of 3D morphology parameters of upper and lower joint surfaces of each specimen are calculated as shown in Table 2.



| No. | Sp(mm) | Sm(mm) | Sh(mm) | Sa(mm) | Sq(mm) | Ss | Sk | SA | Sdq(mm) | Sds×10-3 |
|---|---|---|---|---|---|---|---|---|---|---|
| M1-upper M1-lower |
0.07 0.17 |
-0.28 -0.24 |
0.34 0.41 |
0.60 0.61 |
0.82 0.83 |
1.82 -0.52 |
3.53 3.11 |
1.04 1.06 |
2.06 1.13 |
0.66 2.55 |
| M2-upper M2-lower |
0.22 0.13 |
-0.30 -0.37 |
0.53 0.50 |
0.28 0.31 |
0.41 0.44 |
0.59 -0.43 |
3.97 3.87 |
1.04 1.04 |
0.59 0.57 |
6.35 0.63 |
| M3-upper M3-lower |
0.03 0.04 |
-0.03 -0.06 |
0.06 0.10 |
0.44 0.44 |
0.63 0.63 |
1.06 -0.77 |
3.73 3.30 |
1.05 1.05 |
0.90 0.81 |
3.22 3.27 |
| M4-upper M4-lower |
0.20 0.20 |
-0.41 -0.53 |
0.61 0.73 |
0.33 0.33 |
0.50 0.50 |
-0.90 1.00 |
5.05 5.60 |
1.04 1.04 |
0.81 1.15 |
3.40 2.55 |
| M5-upper M5-lower |
0.01 0.29 |
-0.18 -0.16 |
0.19 0.45 |
0.38 0.37 |
0.54 0.53 |
-0.77 0.77 |
3.35 3.68 |
1.04 1.04 |
0.66 0.73 |
0.67 5.06 |
| M6-upper M6-lower |
0.05 0.55 |
-0.15 -0.09 |
0.20 0.65 |
0.43 0.44 |
0.61 0.63 |
-0.29 0.24 |
5.89 3.31 |
1.05 1.05 |
0.88 0.64 |
3.16 3.81 |
| No. | Sp(mm) | Sm(mm) | Sh(mm) | Sa(mm) | Sq(mm) | Ss | Sk | SA | Sdq(mm) | Sds×10-3 |
|---|---|---|---|---|---|---|---|---|---|---|
| M1 | 0.12 | -0.26 | 0.38 | 0.61 | 0.83 | 0.65 | 3.32 | 1.05 | 1.60 | 1.61 |
| M2 | 0.18 | -0.34 | 0.52 | 0.30 | 0.43 | 0.08 | 3.92 | 1.04 | 0.58 | 3.49 |
| M3 | 0.04 | -0.05 | 0.08 | 0.44 | 0.63 | 0.15 | 3.52 | 1.05 | 0.86 | 3.25 |
| M4 | 0.2 | -0.47 | 0.67 | 0.33 | 0.5 | 0.0 | 5.33 | 1.04 | 0.98 | 2.98 |
| M5 | 0.15 | -0.17 | 0.32 | 0.38 | 0.54 | 0 | 3.52 | 1.04 | 0.70 | 2.87 |
| M6 | 0.3 | -0.12 | 0.43 | 0.44 | 0.62 | -0.03 | 4.6 | 1.05 | 0.76 | 3.49 |
Self-developed radial flowing system for studying the seepage characteristics of single rock joint shown in Fig. (4), includes three parts: water supplying system, loading system, and water collecting system. Water head is controlled by the height of the water tank relative to the rock joint; loading system includes pressure head, upper plate, lower plate, rod, and dial indicator; collecting system mainly includes heat-shrinkable tube (collecting water outflow from rock joint), inlet tube, discharging tube, beaker and balance. The normal stress is calculated by the pump pressure and the section area of rock specimen, and the normal displacement is measured by three equidistant dial indicators which are installed to the rods which are fixed to upper plate. Measuring heads of three dial indicators touch the lower plate fixed to specimen. The reading variation of three dial indicators can reflect the normal displacement between upper plate and lower fixed plate, and it is taken as the normal deformation of rock joint approximately under lower normal stress levels.

By using self-developed radial flowing system (see Fig. 4), the tests of water flowing through a rock joint under different normal stress and different head were carried out at room temperature of 15 °C. The feeding water head were set to 22 m, 17 m, 12 m, 7 m respectively, and normal stress ranged from 1 MPa to 6 MPa with interval of 1 MPa under each feeding water head.
3. RESULTS
3.1. The Relationship Between Flow Rate Per Head and Normal Stress
Relationships between flow rate per head and normal stress for different feeding water head are shown in Fig. (5). From Fig. (5) we can see that the flow rate per head decreases with the increase of normal stress under the four constant water heads. In this respect, Develi and Babadagli [15] found that decreasing trend of transmissivity occurs with increasing normal load in both injection direction after analysis of single-phase flow through rough fracture replicas. In this test, The relationship between flow rate per head and normal stress is well fitted with the negative exponential function; that is, the decreasing rate of flow rate per head decreases with the increase of normal stress. The formula of flow rate per head and normal stress can be expressed as follow:
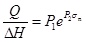 |
(4) |
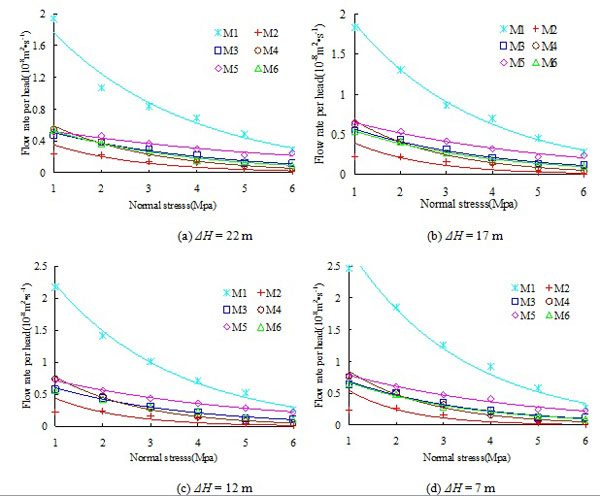
where Q is the flow rate, m3s-1; ΔH is the water head difference, m; P1 and P2 are regression parameters, the units are m2s-1 and MPa-1 respectively; σn is the normal stress, MPa. The regression parameters and the correlation coefficients are shown in Table 3, in which the fitting correlation coefficients R2 are all above 0.70.
| No. | ΔH = 22 m | ΔH = 17 m | ΔH = 12 m | (d) ΔH = 7 m | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | P2 | R2 | P1 | P2 | R2 | P1 | P2 | R2 | P1 | P2 | R2 | |
| M1 | 2.49 | -0.35 | 0.97 | 2.71 | -0.37 | 0.99 | 3.30 | -0.40 | 0.98 | 4.21 | -0.42 | 0.97 |
| M2 | 0.61 | -0.54 | 0.87 | 0.73 | -0.62 | 0.83 | 0.87 | -0.68 | 0.78 | 1.20 | -0.79 | 0.70 |
| M3 | 0.68 | -0.30 | 0.96 | 0.78 | -0.32 | 0.98 | 0.85 | -0.35 | 0.98 | 1.01 | -0.38 | 0.96 |
| M4 | 0.95 | -0.47 | 0.99 | 1.11 | -0.50 | 0.99 | 1.34 | -0.54 | 0.99 | 1.50 | -0.56 | 0.99 |
| M5 | 0.62 | -0.18 | 0.92 | 0.81 | -0.23 | 0.95 | 0.90 | -0.23 | 0.99 | 1.01 | -0.25 | 0.97 |
| M6 | 0.74 | -0.35 | 0.98 | 0.77 | `-0.34 | 0.99 | 0.84 | -0.35 | 0.99 | 0.99 | -0.39 | 0.99 |
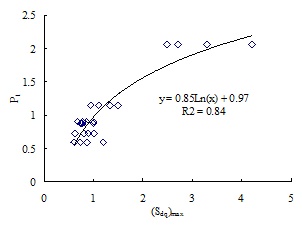
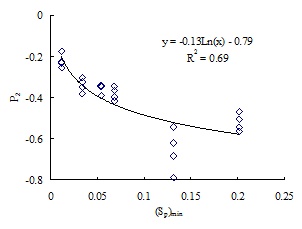
The relationships between P1 and the maximum of root mean square slope (Sdq)max are shown in Fig. (6) and the relationship between P2 and the minimum of peak height on the surface (Sp)min is shown in Fig. (7). As shown in Fig. (6), P1 has a logarithmic function relationship with (Sdq)max and P1 increases with the increase of the maximum of root mean square slope (Sdq)max, and the correlation coefficient R2 is 0.84. According to the empirical formula of JRC and the slope root mean square proposed by Yang et al., [16], the greater the slope root mean square is, the rougher the joint surfaces is, thus P1 is positively related to the roughness of joint surface; when the other parameters are constant in formula (4), the flow rate per head increases with the increase of (Sdq)max. In Fig. (7), P2 decreases with the increase of the minimum of peak height (Sp)min and there is an logarithmic function relationship between P2 and (Sp)min, and as (Sp)min of specimen M2 has an obvious dispersion, the fitting correlation coefficient R2 is only 0.69; on the whole, when the other parameters are constant in formula (4), the flow rate per head decreases with the increase of (Sp)min.
3.2. The Relationship Between Equivalent Hydraulic Aperture and Mechanical Aperture
The relationship between equivalent hydraulic aperture and mechanical aperture are shown in Fig. (8). Equivalent hydraulic aperture is obtained based on the formula of the cubic law, and the mechanical aperture is calculated by subtracting the joint closure under different normal stress from the joint closure under the maximum normal stress. As shown in Fig. (8), the equivalent hydraulic aperture increases with the increase of mechanical aperture, there is a linear correlation between equivalent hydraulic aperture and mechanical aperture, and then the relationship between equivalent hydraulic aperture and mechanical aperture can be expressed as:
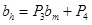 |
(5) |
Where P3 and P4 are regression parameters, in which P3 expresses the slope of the straight line and P4 expresses y-intercept on the vertical axis, and whose value is equal to the initial equivalent hydraulic aperture under the maximum normal stress. Equation (5) is similar to that proposed by Witherspoon et al., [10]. The regression parameters and the correlation coefficients are shown in Table 4, and the correlation coefficients are all above 0.93.
| No. | P3 | P4×10-5 | R2 |
|---|---|---|---|
| M1 | 0. 08 | -4 | 0.99 |
| M2 | 0.13 | -10 | 0.94 |
| M3 | 0.09 | 9 | 0.98 |
| M4 | 0.12 | 7 | 1.00 |
| M5 | 0.04 | -3 | 0.95 |
| M6 | 0.11 | 5 | 0.98 |
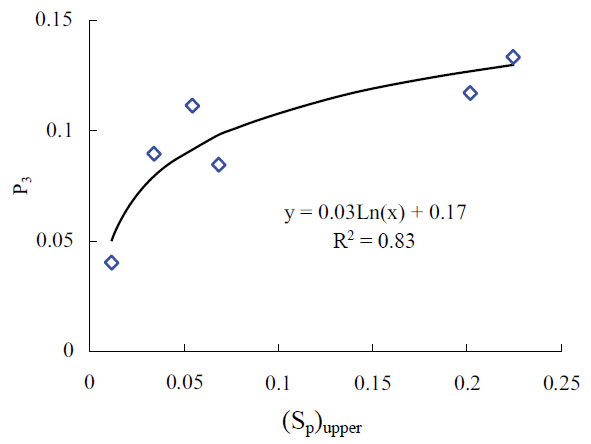
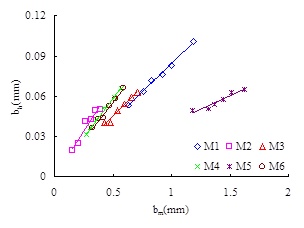
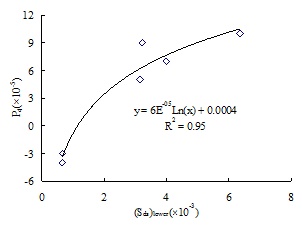
The relationship between P3 and (Sp)upper is shown in Fig. (9), and the relationship between P4 and (Sds)lower is shown in Fig. (10). According to the reference [9], the slope of the straight line P3 is related to the roughness of joint surface, and the value tends to be a constant for smooth parallel plate. From Fig. (9) we can see that P3 rises with increase of the maximal peak height of upper joint surface (Sp)upper; there is a logarithmic function between P3 and (Sp)upper where the fitting correlation coefficient R2 is 0.83; thus, the equivalent hydraulic aperture is positively related to (Sp)upper and (Sp)upper reflects the increasing rate of the equivalent hydraulic aperture with mechanical aperture. As shown in Fig. (10), P4 increases with the increase of the peak average density (Sds)lower, and there is a logarithmic function between P4 and (Sds)lower, where fitting correlation coefficient R2 is 0.95; the bigger the (Sds)lower is, the bigger the initial equivalent hydraulic aperture is.
3.3. Relationship Between Joint Closure and Normal Stress
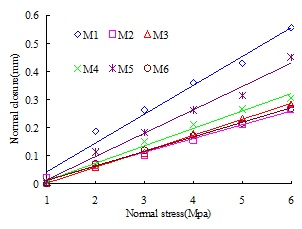
The joint closure is obtained by using the average value of three dial indicator readings under different normal stress. The relationship between joint closure and normal stress is shown in Fig. (11). From that we can see that the joint closure increases with the increase of normal stress, and there is a positive linear relationship between joint closure and normal stress, which is consistent with the results obtained by Giwelli et al., [17], that is:
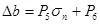 |
(6) |
where Δb is the joint closure, P5 and P6 are regression parameters, in which P5 reflects the change rate of the joint closure, P6 is equal to the initial normal closure under zero normal stress, thus P6 should be zero generally. The regression parameters and correlation coefficients are shown in Table 5, and the correlation coefficients are all above 0.97; as the normal stress ranges from 1MPa to 6MPa, there is mainly the linear compression deformation of joint with the increase of normal stress.
| No. | P5 | P6 | R2 |
|---|---|---|---|
| M1 | 0.10 | -0.06 | 0.98 |
| M2 | 0.05 | -0.03 | 0.99 |
| M3 | 0.06 | -0.05 | 1.00 |
| M4 | 0.06 | -0.05 | 0.99 |
| M5 | 0.08 | -0.07 | 0.99 |
| M6 | 0.05 | -0.04 | 1.00 |
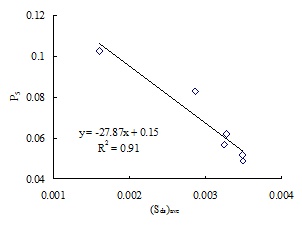
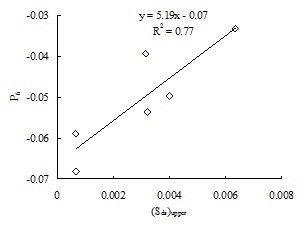
The relationship between P5 and (Sds)ave is shown in Fig. (12), and the relationship between P6 and (Sds)upper is shown in Fig. (13). As shown in Fig. (12), P5 decreases linearly with the increase of (Sds)ave, and it is the negative linear correlation between P5 and (Sds)ave approximately, where the fitting coefficient R2 is 0.91; thus the larger (Sds)ave is, the smaller the joint closure is. From Fig. (13) we can see that P6 increases approximately with the increase of the average peak density (Sds)upper; and it is the positive linear correlation between P6 and (Sds)upper where the fitting coefficient R2 is 0.77; thus, initial joint closure with zero normal stress increases with the increase of (Sds)upper. Besides, as a result of the existence of experimental error, P6 is not always equal to zero.
DISCUSSIONS AND CONCLUSION
The splitting coarse-grained marble joint surfaces were scanned by Tianyuan OKIO-typed three-dimensional laser scanner, and then, the tests of water flowing through a single rock joint are carried out by using the self-developed radial flow system; finally, the relationship between the seepage and mechanical characteristics of rock joint and 3D morphology parameters of joint surfaces are studied. As the tests results, the exponential function between flow rate per head and normal stress, the linear relation between equivalent hydraulic aperture and mechanical aperture, and the linear relation between joint closure and normal stress are found. By analysis of the relationship between the seepage and mechanical characteristics of rock joint and 3D morphology parameters, it is also found that there are close relationships between some 3D morphology parameters of joint surfaces and the regression parameters in equations that express the seepage and mechanical characteristics of rock joint.
The relationship between hydraulic conductivity of rock joint and normal stress without regard to joint roughness is convenient for application, but it can also cause a large error. It can expand the application scope of the formula when regression parameters in the relationship are expressed with morphology parameters of rock joint. Although it is proved that the cubic law is not applicable to rough rock joint, the linear relationship between equivalent hydraulic aperture and mechanical aperture means that the cubic law is applicable in this experiment. Usually, there is a hyperbolic relationship between joint closure and normal stress, but because of a relative small range of normal stress and lack of test data below 1MPa, the linear relationship between joint closure and normal stress seems to be acceptable. In the future, test studies on hydraulic conductivity of rock joint in larger ranges of rock type, joint size, normal stress, and water head should be conducted to master the general law of seepage of rock joint including its size effect. The flow rate of rock joint can be obtained under the condition that the normal stress is known if the morphology parameters could be determined in numerical simulation, which is more credible than simple application of cubic law.
Specifically, the main conclusions are as follows:
- The relationship between flow rate per head and normal stress is well fitted with a negatively exponential function, and the flow rate per head decreases with increase of normal stress; the regression parameter P1 has a logarithmic relation with (Sdq)max and increases with the increase of (Sdq)max, while the regression parameter P2 has a logarithmic function relationship with (Sp)min and decreases with the increase of (Sp)min.
- The equivalent hydraulic aperture has a linear relation with the mechanical aperture and increases with the increase of mechanical aperture; it is a logarithmic function relationship between the regression parameter P3 and (Sp)upper and P3 increases with increase of (Sp)upper; while, it is a logarithmic function relationship between the regression parameter P4 and (Sds)lower and P4 increases with the increase of the (Sds)lower.
- There is a positively linear relationship between joint closure and normal stress and the joint closure increases with the increase of normal stress; there is a negatively linear relationship between the regression parameter P5 and (Sds)ave and P5 decreases with the increase of (Sds)ave; while, there is a the linear relationship between the regression parameter p6 and (Sds)upper and P6 increases with the increase of (Sds)upper.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
This research is supported by the China National Natural Science Foundation (Project Nos. 51109076) and the key scientific and technological project of Henan Province (152102210316).


