All published articles of this journal are available on ScienceDirect.
Nonlinear Volumetric Deformation Behavior of Rock Salt Using the Concept of Mobilized Dilatancy Angle
Abstract
Post-yield strength and deformation properties of rock salt are of great importance to the stability of rock surrounding deep underground storage caverns. Uniaxial and triaxial compression tests were performed to explore the volume change of Qianjiang rock salt under different confining stress states. The experimental results indicate that the dilatancy angle first increases rapidly then decreases gradually and drives to a constant with equivalent plastic strain. A higher confining stress results in a lower peak dilatancy angle. With the increase of confining pressure, the dilatancy angle decreases nonlinearly. Based on the volumetric-axial strain curves of rock salt, a mobilized dilatancy angle model taking into account the effects of confining pressure and the equivalent plastic strain was developed using nonlinear fitting. The new model was implemented in the software FLAC3D and verified effective to predict the volumetric dilatancy behavior of rock salt.
1. INTRODUCTION
Due to the favorable creep, low permeability, and damage-healing properties, rock salt is considered an ideal geologic host rock for underground storage of natural gas and other hydrocarbons. During the last few decades, many tests have been conducted to explore the mechanical properties of rock salt. It is well established that rock salt is a typical soft rock with large deformation and low strength, the deformation and failure mechanisms are governed by the stress state, loading path, strain rate and applied temperature [1-5]. A low confining stress results in a strain softening behavior of rock salt, which turns to strain hardening when the confining stress is higher than a critical value. Rock salt exhibits evident dilatancy along with the initiation and accumulation of micro-cracks in the low confining stress state. The dilatancy gradually degrades with increasing confining pressure, and the deformation behavior of rock salt transits from brittle to ductile [6].
Considerable efforts have been made to assess the nonlinear dilatancy property of rocks in the past few decades. Brace et al. [7] attempted to establish the constitutive equation of rock dilatancy to predict the stress-volumetric strain relationship and the influence of confining pressure. Through the comparison of experimental data for rocks, Jin [8] obtained the mobilized law of volumetric strain change and formulated the corresponding constitutive equation. Zhang et al. [9] suggested the relationship between the dilation angle and the confining pressure of rock using the concept of dilatancy index. Based on triaxial compression test data acquired from published literatures for seven rock types, Zhao and Cai [10] developed a mobilized dilatancy angle model which considers the influence of both confining stress and plastic shear strain according to plasticity theory.
This research aims to experimentally study the dilatancy behavior of rock salt. A mobilized dilatancy angle model considering the effects of both the equivalent plastic strain and confining pressure is proposed and verified to capture the nonlinear volumetric deformation of rock salt adequately.
2. LABORATORY COMPRESSION TESTS
The rock salt cores were extracted from the Tertiary sunken Qianjiang deposit at a depth of 1990-2080 m underground in Hubei Province, China. The samples mainly consist of NaCl with a few impurities of angular grain chipping and mudstone. The color of rock salt changes from gray to black as the content of mudstone increases. The salt specimens were cut into standard cylinders with a diameter-to-length ratio of 1:2, 50 mm in diameter and 100 mm in length. The cylinders were then sawed and grinded without water to ensure the parallelism of the upper and lower end faces within ±0.03 mm. All the compression tests were conducted using the material testing system (MTS311.41) with a loading rate of 0.01-60 mm/min, an axial loading capacity up to 2500 kN. The high-pressure triaxial cell is connected to an electric oil pump via a pressure regulator with a loading capacity of 0-120 MPa.
Conventional triaxial compression tests were performed at lateral confining pressures of 0 MPa, 5 MPa, 10 MPa and 15 MPa with a constant axial strain-controlled rate of 1.0×10−5 s−1. The experimental data set was collected automatically by computer, which consists of axial stress σ1, confining stress σ3, axial strain ε1, and lateral strain ε3. The complete stress–strain curves for rock salt specimens under different confining pressures are shown in Fig. (1).
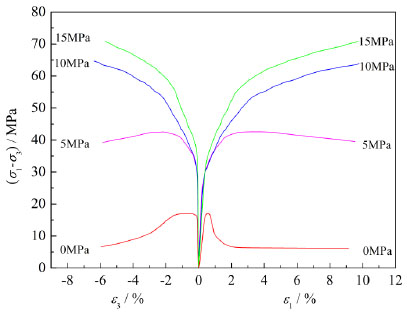
3. MOBILIZED LAW OF DILATANCY ANGLE
Hansen (1958) introduced the concept of “dilatancy angle ψ “, which is a suitable indicator to measure the volumetric increase during rock deformation [11]. In practical rock engineering, the dilatancy angle is normally assumed either zero in a non-associated flow rule or as the same as the friction angle in an associated flow rule. Nevertheless, it is observed that the assumption is not successful in characterizing the nonlinear deformation behavior of rocks [10].
The volume of rock salt decreases due to the closure of the internal micro-cracks during initial compression state. As the axial stress increases to a certain value, the sliding and dislocation takes place in the crystal structure of rock salt accompanied with the newly created cracks, resulting in the final volume increase of salt specimens. Fig. (2) presents the volumetric responses under different confining pressures for Qianjiang rock salt.
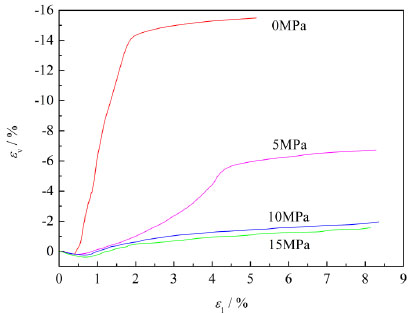
As illustrated in Fig. (2), the onset of dilatancy (the point where volumetric strain curves depart from linearity) delays and the downward trend of volumetric strain becomes smaller as the confining stress increases. In other words, the dilatancy plays a more dominant role at lower confining stress levels. With increasing irrecoverable strain, the post-yield dilatancy gradient (the tangent slope of each point in volumetric-axial strain curve) increases rapidly then decreases gradually after reaching the maximum slope. During the residual stage, the gradient tends to be constant, implying there is no additional volumetric change.
It has been well recognized that the dilatancy angle is closely related to the plastic strain and the confining pressure. The most commonly used expression of dilatancy angle is [12]:
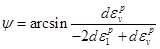 |
(1) |
where εpv=εp1+2εp3 is the volumetric plastic strain, and εp1 and εp3 are the maximum and minimum plastic strain, respectively.
Alternatively, Eq. (1) can be rewritten as:
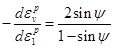 |
(2) |
The slope of irrecoverable strain locus is given by:
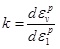 |
(3) |
By substituting Eq. (3) into Eq. (2), the dilatancy angle has the following form:
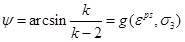 |
(4) |
where εps is the equivalent plastic strain which can be expressed as:
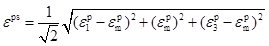 |
(5) |
where εpm=(εp1+εp)/3.
As shown in Fig. (3a), the post-yield unloading path is assumed parallel to the elastic portion of stress-strain curve. An irrecoverable strain locus under different compressing pressures can be obtained by linking all points at intersection of the axial plastic strain (εp1) and the volumetric plastic strain (εp1+2εp3) corresponding to zero deviatoric stress (Fig. 3a). A schematic illustration of establishing the dilation angle of rock salt is given in Fig. (3b and c).
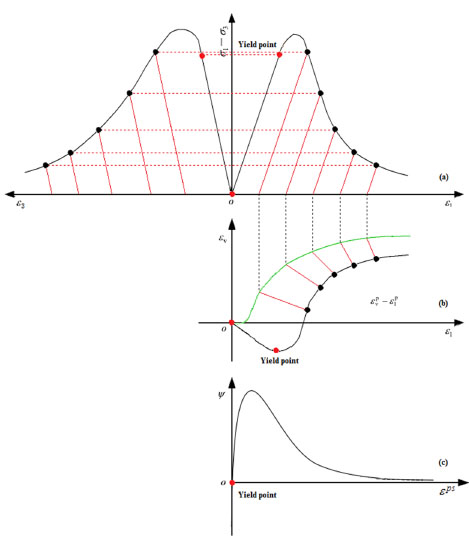
The relation between the dilatancy angle and the equivalent plastic strain of rock salt under different confining pressures was obtained.
The proposed equation of equivalent plastic strain-dependent dilatancy angle under different confining pressures has the expression:
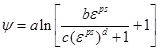 |
(6) |
where a, b, c, d are fitting parameters, εps is in %.
The best-fitting parameters of mobilized dilatancy angle model for rock salt under various confining stresses are summarized in Table 1.
| σ3/MPa | Model parameters | ||||
|---|---|---|---|---|---|
| a | b | c | d | R2 | |
| 0 | 21.23 | 12.60 | 0.01679 | 4.802 | 0.982 |
| 5 | 17.48 | 3.704 | 0.04086 | 4.089 | 0.973 |
| 10 | 12.34 | 2.808 | 0.2056 | 3.489 | 0.760 |
| 15 | 11.88 | 2.448 | 0.2868 | 3.233 | 0.812 |
A high confinement dependence of the parameters (a, b, c, and d) is found in Table 1. The relations of the parameters in Eq. (6) and the confining stress σ3 can be determined by applying empirical formulae. The empirical correlations and best-fitting coefficients are listed in Table 2. The overall fitted results using the mobilized dilatancy angle model are plotted together with the experimental data in Fig. (4).
| Fitted coefficients of Eq. (6) | |||
|---|---|---|---|
| a | b | c | `d |
| a1ea2σ3+a3 | b1e-σ3/b2+b3 | c1σ34+c2σ33+c3 | d1+d2e-d3σ3 |
| 14.02 | 10.06 | -2.202×10−5 | 2.56 |
| -0.08406 | 2.346 | 4.152×10−4 | 2.252 |
| 7.42 | 2.536 | 0.01065 | 0.08292 |
4. VERIFICATION OF DILATANCY ANGLE MODEL
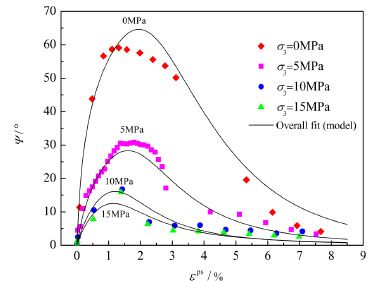
To verify the rationality of the mobilized law for rock salt, the dilatancy angle model combined with a nonlinear cohesion weakening-friction strengthening (CWFS) model [14] is implemented into FLAC3D program utilizing the built-in FISH language. The nonlinear strain dependent cohesion weakening-friction strengthening constitutive model (seen in Fig. 5) was developed to capture the strain softening/hardening behavior of rock salt based on the Mohr–Coulomb criterion.
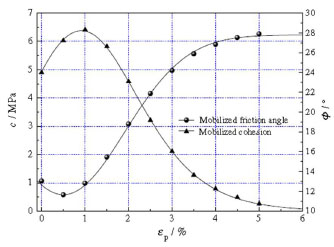
The dimensions of the numerical model are ϕ 50 mm X 100 mm, divided into 2520 zones, as shown in Fig. (6). The displacement at the bottom surface is restricted along the z-direction. Confinement stresses normal to the z-direction are applied to the lateral plane. A constant z-velocity is imposed on the upper boundary with confining pressure unchanged during loading.
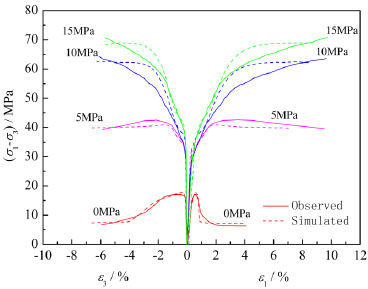
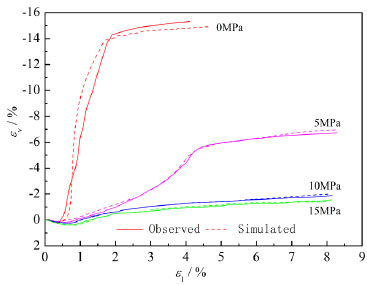
Based on the constructed simulation model, four compression tests at confining pressures of 0, 5, 10, and 15 MPa were performed to obtain the dilatancy responses with the proposed dilatancy angle model. Fig. (7) presents the comparison of the observed and simulated stress-strain curves of rock salt under different confining pressures. Fig. (8) shows the comparison of the observed and simulated volumetric-axial strain curves of rock salt under different confining pressures.
As seen in Fig. (8), the predicted nonlinear volumetric responses by the mobilized dilatancy angle model agree well with the experimental results of rock salt from low to high confining pressure. The volumetric increase of rock salt is more remarkable at lower confining pressure. The dilatancy angle exhibits a higher dependence of the equivalent plastic strain. It is concluded that the mobilized dilatancy angle model can effectively capture the dilatancy property of rock salt with respect to the plastic strain and confining stress.
CONCLUSION AND FUTURE RESEARCH
The post-yield strength and deformation properties of rock salt play an important role in the study of the progressive failure and convergence deformation of the rock mass around an underground storage cavern.
The post-yield dilatancy responses of Qianjiang rock salt with respect to the equivalent plastic strain and the confining pressure were obtained based on the stress-strain curves and the volumetric-axial strain curves observed. The rock salt exhibits a higher dilatancy deformation at a lower confining pressure. The volumetric dilatancy degrades dramatically with increasing confinement. Nevertheless, the dilatancy angle is more sensitive to the equivalent plastic strain.
A plastic strain and confining stress-dependent dilatancy angle model was proposed to characterize the volumetric change of rock salt. The mobilized dilatancy angle model in combination with the mobilized strength parameters has been verified to describe the dilatancy behavior of rock salt reasonably through numerical simulation. The new developed model provides a theoretical basis for analyzing the stability of surrounding rock in underground salt caverns. The applicability for other rock types needs to be further studied.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
This research has been financed and fully supported by the National Basic Research Program of China (973 Program, No.2013CB036005), the National Natural Science Foundation of China (Grant Nos. 51527810, 51309234, and 51304219), which are greatly appreciated by the authors. The authors also thank the financial support of the Natural Science Foundation of Jiangsu Province (BK20130065), and the Open Foundation of State Key Laboratory for Geomechanics and Deep Underground Engineering (SKLGDUEK1403), and the China Postdoctoral Science Foundation (2015M570451).


