All published articles of this journal are available on ScienceDirect.
Theoretical and Experimental Study on Natural Frequency of Externally Prestressed Box-Girder with Corrugated Steel Webs
Abstract
Based on the characteristics of box girder with corrugated steel webs, the existing prestressing force, the effect of shear deformation of composite girder on the deflection, “folding effect” in longitudinal direction of corrugate steel webs and the arrangement of external tendons were considered comprehensively. With the experiment results of five literatures integrated, N/fcA (the axial compression ratio) was selected as regression parameter to develop a regression equation for the effective cross-section stiffness of the girder. Then a formula for natural frequency of the externally prestressed box girder with corrugated steel webs was proposed. Finally, the in-situ measurement on an actual bridge and a laboratory dynamic test on the model box girder with seven prestressing levels were conducted. The test results showed that the natural frequency of box girders with corrugated steel webs increased along with the growing external force. In contrast to other related formulas, the calculated results of the formula proposed in this paper showed the same tendency with measured results and the maximum error is 1%.
1. INTRODUCTION
In the recent years, the externally prestressed box girder with corrugated steel webs as a possible means of lightening weight, enhancing seismic performance and improving prestressing efficiency has drawn widespread attention worldwide. Several previous studies focusing on the statistic behavior of box girder with corrugated steel webs, such as shear behavior, flexural behavior, torsional behavior and shear lag effect, have been carried out in the recent decades. Serving as the principal compressed component of the cross-section, the concrete roof and floor of the box girder with corrugated steel webs determines the safety and function of the structure to a great extent. Long-term effects of concrete, i.e. shrinkage and creep, may lead to not only excessive deflections of bridges but also a deterioration of the prestress in external tendons over time, which can severely curtail the life span and put the bridge out of service [1-3]. The theoretical analysis revealed that the fundamental frequency of the simply supported prestressed beam fell off to less than 50% of the original frequency as a result of long-term behavior of concrete [4]. In-situ monitoring of creep and shrinkage effects in a real post-tensioned concrete box girder during construction and service was also performed in order to contribute knowledge to design practice [5].
Whereas, there are rare researches on the dynamic behavior of box girder with corrugated steel webs thus far. Even though some scholars investigated the effect of external prestressing on the natural frequency of box girder with corrugated steel webs, they ignored the arrangement of tendons and lacked of either analytical or experimental proofs [6-9]. As replacing the thick concrete webs with corrugated steel webs, the mechanical performance of box girder with corrugated steel webs differs significantly from that of classical concrete box girder and the calculation theories need to be innovated in addition to the general beam theory. Considering the distinctive feature of box girder with corrugated steel webs, this paper aims at the natural frequency of externally prestressed box girder with corrugated steel webs with the existing of prestressing force, the shear deformation of composite girder, “folding effect” in longitudinal direction of corrugate steel webs and the arrangement of external tendons taken into account comprehensively. As a first step, a formula for natural frequency of the externally prestressed box girder with corrugated steel webs was derived from a natural frequency equation obtained using a distributed-mass beam model. Then in-situ measurement on an actual bridge and a laboratory dynamic test on the model box girder with seven prestressing levels were conducted. Consequently, experimental measurements of natural frequency and values obtained from the formula were compared to verify the effectiveness and accuracy of the proposed formula.
2. LITERATURE REVIEW
In 1994, Saiidi et al. [6] proposed an equation for the natural frequency of a simply supported axially compressed beam. The authors took the prestressing force as the axial force on beam and the stiffness was modified by field test and laboratory experiment. The relationship between the equivalent stiffness and axial force was shown as:
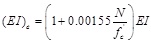 |
(1) |
where (EI)e is the effective stiffness; N is the axial pressure (kN), and the approximate value of N is Pt 0; f 'c is the concrete compressive strength (MPa).
However, the arrangement of tendons and the eccentricity due to beam vibrations were not considered in Saiidi’s paper, which subsequently has been followed by three discussions: Dallasta et al. [10] indicated that the effect of the prestressing force on the natural frequencies of beams was negligible using the Kirchhoff kinematic model. And the phenomena of different origin, such as cracking, may produce more sensible effects in real cases. Deak et al. [11] claimed that the method of calculation of Saiidi was erroneous and prestressing force could not reduce the natural frequency of beams in either case. Jain et al. [7] disagreed with Saiidi regarding the change in frequency due to “compression softening” effect of the prestressing force. They believed that the only major effect of prestressing loss on natural frequencies of the beam was through opening of microcracks in the concrete. Nevertheless, no detailed analytical and experimental proofs were given in the above discussions.
On the basis of Saiidi’s theory, Liu et al. [12] considered the impact of cross-section shape and the introduced prestress on the effective stiffness of box girder with corrugated steel webs and proposed the regression formula:
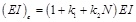 |
(2) |
where N is the effective prestressing force(kN); k1 and k2 are the experiment constants related with the shape of cross section.
Similarly, Xie [13] built a regression relationship between the effective dynamic stiffness and prestressing force through the indoor model test on a rectangular beam. The empirical formulas was as follows:
 |
(3) |
where Ny is the effective prestressing force(N); fc is the concrete compressive strength (Pa).
Based on the dynamic test of two full-prestressed concrete beams, Zhang et al. [14] discussed the stiffness change resulted from the change of elastic modulus, then a modified formula was proposed as:
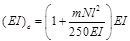 |
(4) |
where m is the mass of girder per unit length(kg); N is the prestressing force (kN).
According to the dynamic test on externally prestressed simply supported concrete beams separately with three typical types of tendon distributions, Xiong et al. [15] adopted two methods to correct the rigidity parameter in the formula for the natural frequency of the concrete beam. Then the following corrected formulas was obtained:
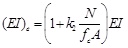 |
(5-1) |
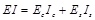 |
(5-2) |
where Ec is the elastic modulus of concrete; Ic is the geometrical moment of inertia of the cross-sectional area of concrete; Es is the elastic modulus of steel; Is is the geometrical moment of inertia of the vertical reinforcement bar; k2 is the correction coefficient (k2=0.7, 2.8 and 2.1 for a beeline beam, single folder linear beam and double-fold linear beam, respectively); N is the prestressing force (kN); fc is the compressive strength of concrete (MPa).
Some literatures [12-15] recommended that the natural frequency of the simply-supported beam increased as prestressing force increasing. However, some researchers obtained completely different and converse conclusions. Based on the Rayleigh-Ritz formulation which described prestressing force as the external axial compressive force only, Kanaka et al. [16] showed that the prestressing force reduced the low-order frequencies of prestressed beams. Assuming that there was a greater deformation and deflection angle in the unbounded prestressed beam, Hamed et al. [8] rigorously derived the equations of motion for the beam and drew the conclusion that the natural frequency was not affected by unbounded prestressed tendons. But this claim was not supported by some experimental phenomena [12, 13].
Traditionally, the internal tendons were not regarded as a separate component in the calculation of the bending vibration of prestressed beams. Nevertheless for externally prestressed structures, the external tendons were bonded with main structure only at steering blocks and anchors and can be perceived as an independent component, thus the relevant research results about the internally prestressed beams cannot be applied indiscriminately herein. During the vibration analysis on the externally prestressed concrete beam, the vibration of external tendons should also be taken into account. Miyamoto et al. [17] considered the arrangement of external tendons and deduced the equation for the influence of external prestressing on the natural frequency using a distributed-mass beam model, but the effect of prestressing force on the section stiffness was not fully considered. Xiong et al. [9] improved and extended the Miyamoto’s formula to propose some formulae for natural frequency with the external tendons arranged in three different configurations. Many factors were considered in the analysis of Xiong’s paper [9] and some effective anti-vibration measures were provided. Whereas the corresponding experimental verification was lacked. Considering concrete as a composite material, Xiong et al. [18] carried out dynamic tests on three simply supported beams with external prestressing. The experimental results indicated that natural frequencies of specimens increased with the growth of prestressing during tension phase, which is contrary to what derived from the classical linear-plastic theory. But the shear deformation of the girder was not considered. On the contrary, Park et al. [19] carried out dynamic tests on an actual bridge with external prestressing, and the test results showed that external prestressing had no effect on the natural frequency of the girder. Zhang et al. [20] discussed the natural vibration frequency of the external prestressed beam by perturbation method, pointing out that the fundamental frequency of the beam slightly declined with increasing prestressing force.
The box-girder bridge with corrugated steel webs is an innovative kind of concrete-steel composite structure which employs corrugated steel webs instead of concrete webs. For this reason, the shear deformation of composite girder and “folding effect” in longitudinal direction of the corrugate steel webs should be considered in analysis [21-23]. The prestressed reinforcement cannot be arranged in the slender steel webs, thus a large amount of external tendons need to be anchored in the box girder to withstand the loads. At present, the external prestress technology has been widely used with a tendency that the fully external prestressed structure was adopted in some countries, especially in Japan [24]. Therefore, it is particularly important to study the dynamic characteristics of the composite box girder with corrugated steel webs considering external prestressing. Zhang et al. [25] calculated the natural frequency of a test box girder with corrugated steel webs using a formula for calculating the frequency of an externally prestressed simply supported beam. In calculation case, the characteristics of the section of box girder with corrugated steel webs were considered. The results showed that the natural frequency of the composite girder after prestressed was larger than that before prestressed, which meant the natural frequency of the girder tended to increase with the prestressing force applied. On the contrary, Chen et al. [26] convinced that the external tendons reduced the natural frequency of prestressed box girder with corrugated steel webs by about 3% based on Miyamoto’s method, however the effect of the existing prestressing force on cross-section stiffness was not considered by Zhang [25] and Chen [26].
3. DERIVATION OF NATURAL FREQUENCY FORMULA
3.1. Analysis Model and Basic Assumptions
Analysis model of a double broken line prestressed composite box girder with corrugated steel webs is shown in Fig. (1).
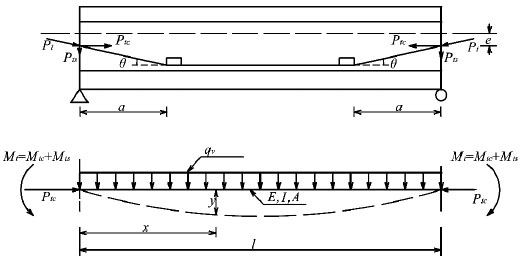
where e is the eccentricity distance from neutral axis; a is the horizontal distance between steering block and anchor point; θ is the steering angle of the tendon; y is the vibration displacement; Pt 0 is the initial prestressing force; Ptc 0 is the horizontal component of initial prestressing force; Pts 0 is the vertical component of initial prestressing force; ΔPt is the increment of prestressing force due to flexural vibration; l is the span length; qv is the distributed mass; x is the horizontal distance between calculation section and anchor point; E is the elastic modulus of concrete; I is the moment of inertia of composite girder, A is the cross-sectional area. The prestressing force Pt is expressed as:
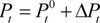 |
(6) |
The horizontal component of prestressing force Ptc is represented as:
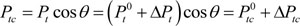 |
(7) |
The vertical component of prestressing force Pts is represented as:
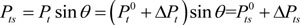 |
(8) |
The bending moment due to prestressing force Mt is represented as:
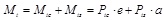 |
(9) |
The following basic assumptions are adopted in the calculation:
- As the effect of shear slip between the concrete slab and corrugated steel web is negligible, it is assumed that the cross section of the composite girder is uniform [27].
- The vibration displacement of the composite girder is minimal, so the curvature of the girder can be rationally expressed as
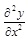 based on the small deformation theory.
based on the small deformation theory.
- Due to the “folding effect” in longitudinal direction of the corrugate steel webs, the longitudinal stress and strain in the corrugated steel webs is approximate to 0, so a quasi-plane assumption [28] (given the corrugated steel webs were removed away and the concrete roof and floor were linked up to establish a virtual plane) is adopted for strain distribution across the cross-section of the girder.
- Axial deformation of the beam is ignored; the compressive stress and the corresponding strain are negligible.
3.2. Formula Derivation
The vibration differential equation of the box girder with corrugated steel webs subjected to external prestressing force is expressed as follows:
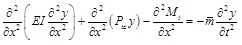 |
(10) |
where 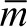 is the mass of composite girder per unit length.
is the mass of composite girder per unit length.
Substituting Eq.7-Eq.9 into Eq.10, the following equation can be obtained:
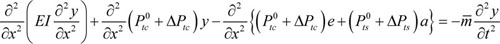 |
(11) |
where Ptc 0 and Pts 0 are independent of x. Since the maximum value of vibration displacement ymax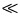 e and therefore ΔPtc ∙ y
e and therefore ΔPtc ∙ y 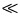 ΔPtc ∙ e, the value of ΔPtc ∙ y is negligibly small. Hence, Eq.11 can be rewritten as:
ΔPtc ∙ e, the value of ΔPtc ∙ y is negligibly small. Hence, Eq.11 can be rewritten as:
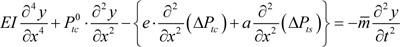 |
(12) |
As the increment of prestressing force due to flexural vibration, ΔPt is proportional to the maximum value of y. Therefore, if it is assumed that the vibrational displacement is infinitesimal, ΔPt can be calculated from diagram multiplication:
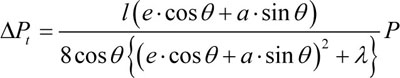 |
(13) |
where Es is the elastic modulus of external tendons; As is the cross-sectional area of external tendons; and ls is the length of the tendon; λ is given as:
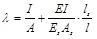 |
(14) |
In order to calculate the increment of prestressing force due to flexural vibration, a concentrated load was exerted at midspan of the model girder herein. The influence of shear deformation on the deflection of the box girder with corrugated steel webs was considered.
J. Cafolla et al. reported a decrease in the shear modulus of corrugated steel webs under shear force and established the formula for equivalent shear stiffness of box girder with corrugated steel webs [29]:
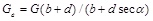 |
(15) |
where G is shear elastic modulus of steel; b, d and α are illustrated in Fig. (2).

Then the midspan deflection yp (the maximum value of y) due to the applied load P can be calculated from the equation in [30]:
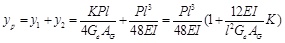 |
(16) |
where y1 is the mid-span deflection produced by shear; y2 is the mid-span deflection produced by bending moment; AG is the shear area of corrugated steel webs. K is the stress non-uniform coefficient. Based on the mechanical characteristics of the box girder with corrugated steel webs, the shear force is totally born by the thin steel webs, so K is fixed as 1.
Given
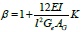 , Eq.16 can be expressed as:
, Eq.16 can be expressed as:
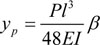 |
(17) |
Substituting Eq.13 into Eq.17:
 |
(18) |
The upward movement of the girder yΔpt due to ΔPt can be calculated as:
 |
(19) |
Based on the relationship y = yp - yΔPt , Eq.18 and Eq.19, y can be calculated as:
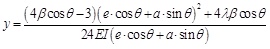 |
(20) |
Therefore ΔPt can be expressed as the function of y according to Eq.20:
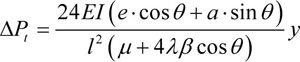 |
(21) |
where μ is given as:
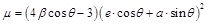 |
(22) |
Substituting Eq.21 into Eq.12:
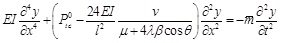 |
(23) |
where ν is given as:
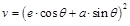 |
(24) |
Eq. 23 is the equation for undamped free vibration of the girder, which can be solved by separation variable method.
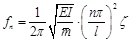 |
(25-1) |
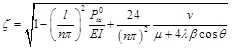 |
(25-2) |
where fn is the natural frequency of the girder(Hz); n is the order of natural frequency, if n=1, f1 is fundamental frequency; ζ is the correction coefficient.
 in Eq.25-1 is the equation based on general beam theory [31], manifesting that the natural frequency of simply supported beam with uniform rectangular cross-section only relates to the mass of the girder per unit length, span length and cross-section stiffness. ζ is a correction coefficient taking account of the characteristics of box girder with corrugated steel webs, the shear deformation of composite girder and the influence of both prestress force and arrangement of external tendons on section stiffness.
in Eq.25-1 is the equation based on general beam theory [31], manifesting that the natural frequency of simply supported beam with uniform rectangular cross-section only relates to the mass of the girder per unit length, span length and cross-section stiffness. ζ is a correction coefficient taking account of the characteristics of box girder with corrugated steel webs, the shear deformation of composite girder and the influence of both prestress force and arrangement of external tendons on section stiffness.
It is well established that the corrugated steel webs of composite box-girder can deform freely in longitudinal direction, which is called “folding effect”, therefore its axial and bending stiffness are negligible. Considering this effect, the cross-section stiffness of the composite girder can be simplified as the stiffness of concrete roofs and floors only, as expressed in the following:
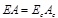 |
(26-1) |
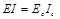 |
(26-2) |
where Ec is the elastic modulus of concrete; Ac is the cross-sectional area of concrete in roof and floor, Ic is the moment of inertia of the concrete components of cross-section.
In addition, during the tensioning process, the cross section remains uniform and no cracking occurs if the tensioning control stress is not large (Ptc≤0.3fpk, where fpk is the tensile strength of the external tendons).
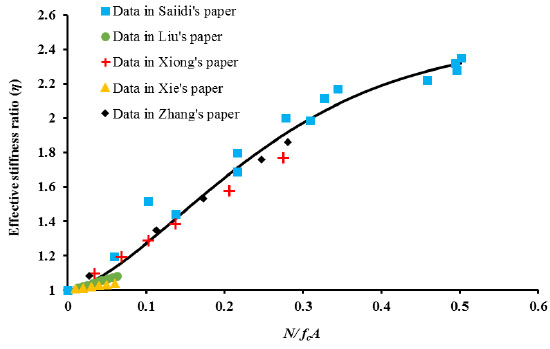
With a series of concrete compressive strength, the papers of Saiidi [6], Liu [12], Xie [13], Zhang [14] and Xiong [15] show a remarkable difference in the change rate of effective stiffness. The parameter η was defined as the effective stiffness ratio which accounts for the influence of diverse axial forces on the section stiffness. The lower the concrete compressive strength is, the faster η changes. For the beam with the compressive strength of concrete was 50.09MPa in Xie’s paper, η ranged from 1 to 1.038 with N/fcA varied from 0 to 0.0599, which indicates the slightest variation in η. Whereas in Saiidi’s paper, the 28-day compressive strength of concrete was 20.3 MPa, and η ranged from 1 to 2.352 with N/fcA varied from 0 to 0.501, manifesting the most significant impact on cross-section stiffness. With the test results of all five papers integrated, it is reasonable to propose that the rate of η change correlates with prestressing force as well as the compressive strength of concrete. So the regression parameter N/fc A (axial compression ratio) was selected to develop a regression equation for effective stiffness, which can be written in the form:
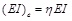 |
(27-1) |
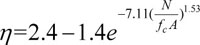 |
(27-2) |
The related coefficient is 0.989, which means that the equation fits well with the data. The regression curve of effective stiffness ratio is shown in Fig. (3).
Substituting Eq.27 into Eq.25:
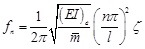 |
(28-1) |
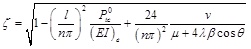 |
(28-2) |
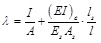 |
(28-3) |
When external tendons are arranged in i different configurations, Eq.28 is extended as:
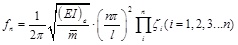 |
(29-1) |
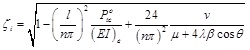 |
(29-2) |
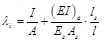 |
(29-3) |
Compared with general beam theory, the shear deformation of box girder with corrugated steel webs, “folding effect” in longitudinal direction of the corrugate steel webs, the effect of the existing prestressing force on stiffness and arrangement of external tendons are all considered in this paper.
4. EXPERIMENTAL VALIDATIONS
To verify the efficiency and accuracy of the proposed analysis, field testing and laboratory experiment were carried out, respectively.
4.1. Field testing
Fig. (4) shows San Dao-he Bridge in Qinghai Province, which is a simply supported concrete box girder bridge with corrugated steel webs and effective span length is 49.92m. Fig. (5) presents the cross section of San Dao-he Bridge. The strength grade of concrete slabs is C50, whose mechanical properties can be referred to the Code for Design of Concrete Structures [32]. Q345 steel was used as the corrugated steel webs with the thickness of 12mm and its properties were in accordance with the standard of Carbon Structural Steels [33]. The lengths of horizontal and inclined panels are 430mm and 370mm, respectively, and the wave height is 220mm.

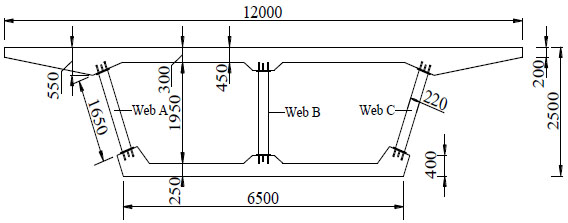
There are 14 bundles of external tendons; each of them consists of 13 strips of steel strand with 1395MPa tensioning control stress. The layout of external tendons is double broken line. External tendons are turned at the inner diaphragms which are closest to side diaphragms and anchored at side diaphragms. Detail information for external tendons is listed in Table 1.
| Specimen | ls(m) | A(mm2) | (m) | θ(°) | a(m) |
|---|---|---|---|---|---|
| 1 | 52.36 | 7228 | -0.5 | 7 | 12.16 |
| 2 | 52.28 | 7228 | -0.05 | 6 | 12.16 |
| 3 | 52.24 | 7228 | 0.4 | 6 | 7.36 |
| 4 | 52.18 | 3614 | 0.95 | 2 | 7.36 |
The San Dao-he Bridge was subjected to ambient vibration test to attain its fundamental frequency. Without traffic load on the bridge deck and regular vibration source near the bridge site, the microseism of the bridge excited by stochastic loads, e.g. wind load, micro-tremor and flow, was catch by the data acquisition instrument INV306U-5160 made by China Orient Institute of Noise & Vibration. Eleven tested cross sections symmetrical to the mid-span were arranged on the bridge, and there were two measuring points for each cross section, as presents in Fig. (6).
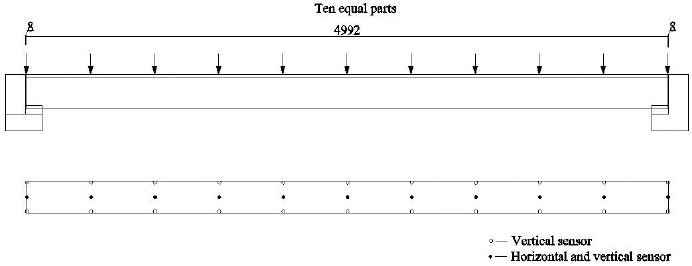
DASP (Data Acquisition & Signal Processing) was employed as the analysis system. The theoretical results and the measured values of the fundamental frequency of the bridge are compared in Table 2.
| Specimen | Measured result (1) | General Beam Theory (2) | Miyamoto’s Theory (3) | Theory in this paper(4) |
|---|---|---|---|---|
| Fundamental frequency (Hz) | 2.734 | 2.434 | 2.386 | 2.581 |
| Relative error (%) | — | -10.9 | -12.7 | -5.6 |
The measured natural frequency is the biggest of all and the relative errors are -10.9%,-12.7% and -5.6% for (2), (3) and (4) cases, respectively. The result calculated by the theory in this paper is nearest to measured result and the fundamental frequency increases with external prestressing taken into account.
4.2. Laboratory Experiment
In order to further explore the influence law of prestressing force on the natural frequency, the dynamic characteristic test on a simply supported prestressed composite girder with seven prestressing levels was conducted. Since the fundamental frequency of girder is noticeably affected by the external prestressing while there is no regularity for the high-order frequencies to follow [17], the fundamental frequency of model girder was measured merely in this research.
Fig. (7) shows the model box girder, which is a simply supported concrete box girder with corrugated steel webs and the span length is 4400mm. Fig. (8) presents the cross section of the model hybrid girder. The compressive strength of concrete slabs is 22.4 MPa, whose elastic modulus is 27000MPa. Q345 steel was used as the corrugated steel webs with the thickness of 4mm and its properties were in accordance with the standard of Carbon Structural Steels [33]. The lengths of horizontal and inclined panels are 150mm and 125mm, respectively, and the wave height is 60mm.

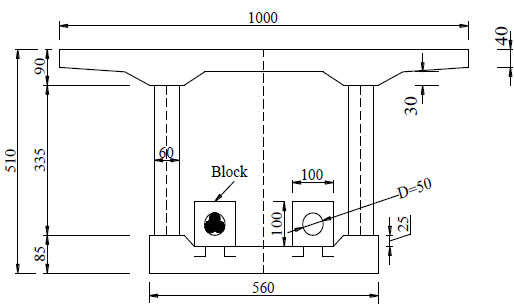
There are two bundles of external tendons; each of them consists of 3φj15.2 steel strands with 1860 MPa tensioning control stress. The sectional area of each φj15.2 steel strand is 139mm2.The layout of external tendons is double broken line. External tendons are turned at the inner diaphragms which are closest to side diaphragms and anchored at side diaphragms. Detail information for external tendons is listed in Table 3.
| Specimen | ls(mm) | A(mm2) | (mm) | θ(°) | a(mm) |
|---|---|---|---|---|---|
| 1 | 4416 | 417 | 41 | 7 | 1100 |
| 2 | 4416 | 417 | 41 | 7 | 1100 |
The fundamental frequency was measured by impact hammer test. In general, sensors are located at the girder where deformation is relatively larger, and the nodes of mode shape should be avoided lest missing some important modal information. It is well established that the mid-span deflection is maximum for simply supported girder in the first mode of vibration, so an accelerometers was deployed at the mid-span section. WS-5924 produced by Beijing Wave spectrum & Science & Technology Co., Ltd. was employed as the acceleration data collection system, as shown in Fig. (9).

There were five hammering points arranged at the model girder, as illustrated in Fig. (10). Two rounds of hammering were conducted for each prestressing level. With the time-domain curves of hammering force signal and acceleration signal recorded, as shown in Figs. (11 and 12), the fundamental frequencies of the model girder with seven prestressing levels can be obtained by modal analysis software.
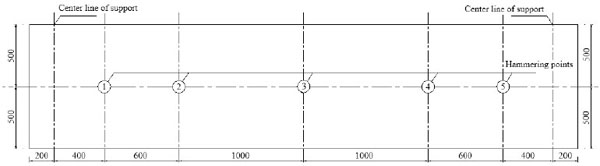

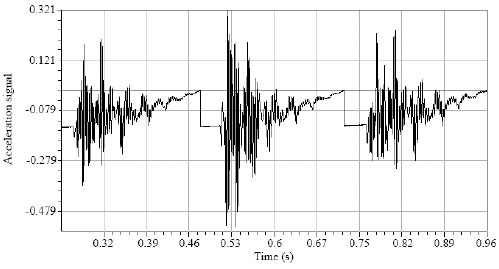
The measured and calculated results are listed in Table 4. Fig. (13) shows the comparison between calculated and measured results of the model box girder.
| Prestressing force (kN) (1) |
Experimental (Hz) (2) | General Beam Theory | Miyamoto’s Theory [17] | Theory in this paper | |||
|---|---|---|---|---|---|---|---|
| Calculated (Hz) (3) |
Relative error (%) (4) |
Calculated (Hz) (5) |
Relative error (%)(6) |
Calculated (Hz) (7) | Relative error (%)(8) | ||
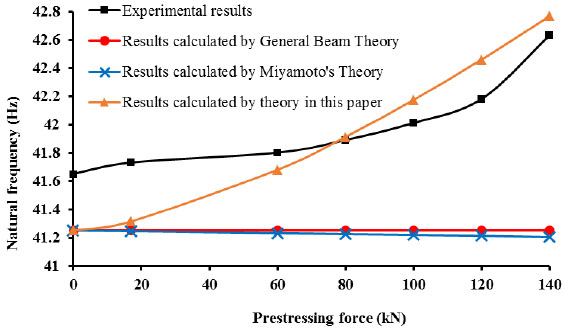
| 0 | 41.65 | 41.251 | -0.96 | 41.251 | -0.96 | 41.251 | -0.96 |
| 17 | 41.73 | 41.251 | -1.15 | 41.246 | -1.16 | 41.314 | -1.00 |
| 60 | 41.8 | 41.251 | -1.31 | 41.232 | -1.36 | 41.680 | -0.29 |
| 80 | 41.89 | 41.251 | -1.53 | 41.225 | -1.59 | 41.913 | 0.05 |
| 100 | 42.01 | 41.251 | -1.81 | 41.219 | -1.88 | 42.174 | 0.39 |
| 120 | 42.18 | 41.251 | -2.20 | 41.213 | -2.29 | 42.461 | 0.67 |
| 140 | 42.63 | 41.251 | -3.23 | 41.203 | -3.35 | 42.768 | 0.32 |
With the desired prestress force applied and the prestressed steel strands anchored properly, dynamic tests were carried out on the box girder. The data (2) in Table 4 clearly indicate that the measured fundamental frequency increases nonlinearly along with the growing prestressing force, and the maximum increase is 2.35%. The results (3) calculated by general beam theory do not change, for the natural frequency only concerns with E and I, and has nothing to do with the prestressing force outside. The calculated results (7) show an increase of nearly 3.68% in the fundamental frequency as the prestressing force changed from 0 to 140kN, which is slightly larger than the maximum increase in the test. This phenomenon may be explained by the fact that the induced compressive stress in concrete dramatically affects the safety and function of prestressed composite structures, where long term effects, i.e. shrinkage and creep in concrete and relaxation of prestressing external tendons, lead to a decrease of the stress in concrete over time [1, 2], which has a softening effect on the cross-section stiffness of the composite girder based on Eq.27. Consequently, according to Eq.29, the measured fundamental frequency of the girder decreases to some degree.
In contrast, the calculated results (5) show a 0.1% reduction in the natural frequency, which is opposite to the tendency of measured results. The results calculated by the formula in this paper show the same tendency with the measured results, and the maximum relative error for (7) is 1%. This is because that the effect of the existing prestressing force on stiffness, the shear deformation of the box girder, “folding effect” in longitudinal direction of the corrugate steel webs and the arrangement of external tendons are all considered. Therefore, the proposed formula can provide a reference for the dynamic design of prestressed structures. However, due to different test programs and measurement systems, whether the results can give guidance to other concrete structures accurately should be studied further; besides, the long term effects of the concrete components of the cross-section on the loss of prestress forces need further investigations.
CONCLUSION
- Based on the characteristics of box girder with corrugated steel webs, the existing prestressing force, the effect of shear deformation of composite girder on the deflection, “folding effect” in longitudinal direction of corrugate steel webs and the arrangement of external tendons were considered comprehensively. Then a formula for natural frequency of the externally prestressed box girder with corrugated steel webs was proposed.
- The in-situ measurement on the fundamental frequency of an actual box girder with corrugated steel webs was carried out. Compared with other theoretical calculation results, the result calculated by the theory in this paper is nearest to measured result and the fundamental frequency increases with external prestressing taken into account.
- The laboratory dynamic characteristic test on a simply supported prestressed composite girder with seven prestressing levels was conducted. The test results show that the natural frequency of box girders with corrugated steel webs increases along with the growing external force. In contrast to other related formulas, the calculated results of the formula proposed in this paper show the same tendency with measured results and the maximum error is 1%.
LIST OF ABBREVIATIONS
| θ | = the steering angle of the tendons |
| ΔPt | = the increment of prestressing force due to flexural vibration |
| ζ | = the correction coefficient |
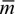 |
= the mass of composite girder per unit length |
| a | = the horizontal distance between steering block and anchor point |
| A | = the cross-sectional area |
| Ac | = the cross-sectional area of concrete in roof and floor |
| AG | = the shear area of corrugated steel webs |
| As | = the cross-sectional area of external tendons |
| e | = the eccentricity distance from neutral axis |
| E | = the elastic modulus of the girder |
| Ec | = the elastic modulus of concrete |
| Es | = the elastic modulus of external tendons |
| fn | = the natural frequency |
| fpk | = the tensile strength of the external tendons |
| G | = the shear elastic modulus of the steel |
| Ge | = the equivalent shear stiffness of box girder with corrugated steel web |
| I | = the moment of inertia of composite girder |
| Ic | = the moment of inertia of the concrete components of cross-section. |
| K | = the stress non-uniform coefficient |
| l | = the span length |
| ls | = the length of the tendon |
| Mt | = the bending moment due to the prestressing force |
| n | = the order of natural frequency |
| Pt | = the prestress force |
| Pt0 | = the initial prestressing force |
| Ptc | = the horizontal component of prestressing force |
| Ptc0 | = the horizontal component of initial prestressing force |
| Pts | = the vertical component of prestressing force |
| Pts0 | = the vertical component of initial prestressing force |
| qv | = the distributed mass |
| x | = the horizontal distance between calculation section and anchor point |
| y | = the vibration displacement |
| y1 | = the mid-span deflection produced by shear |
| y2 | = the mid-span deflection produced by bending moment |
| yp | = the midspan deflection |
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
This research was supported by Science and Technology Project of West Traffic Construction of China (200831822367).


