A Review on Adaptive Methods for Structural Control

All published articles of this journal are available on ScienceDirect.

REVIEW ARTICLE

A Review on Adaptive Methods for Structural Control

Ilaria Venanzi, * Open Modal
Authors Info & Affiliations
The Open Civil Engineering Journal • 31 Oct 2016 • REVIEW ARTICLE • DOI: 10.2174/1874149501610010653

Abstract

Adaptive control algorithms are widely used in many technical fields like aeronautics and robotics for controlling systems whose characteristics vary with time or are uncertain. In the last decades, with the diffusion of active and semiactive control applications in civil engineering, adaptive methods started to be adopted for structural control. This paper provides an up-to-date survey on strategies currently available for adaptive control and a literature overview of solutions examined until today for structural applications.

Keywords: Active control devices, Adaptive control, Control algorithm, Non-linearity, Saturation, Uncertainty.

1. INTRODUCTION

In the last decades, a large effort has been made to develop innovative methods for vibration mitigation in civil engineering structures, like buildings, long-span bridges and slender towers that may experience significant dynamic response under wind and seismic loads [1-3]. Among innovative solutions for vibration mitigation, active control has gained an increasing interest, mainly due to technological developments which have made feasible the adoption of active control solutions in real structures. Full-scale applications of active control are essentially dominated by the use of active mass driver (AMD) systems [4-6], that are composed by a servo-actuator moving a mass in order to generate an inertial force that is used for active damping. More recently, semiactive devices, like megnetorheological and electrorheological dampers, started to become widespread in structural applications [7-9]. They associate the reliability of passive devices to the versatility and effectiveness of active devices and cannot produce instability as they do not inject energy to the structure [10]. Viable alternatives are also active and semiactive tendon systems [11, 12] and active and semiactive base isolation [13, 14].

The effectiveness of active control depends on the selected control algorithm. Linear control algorithms, like Linear Quadratic Regulator (LQR) and Direct Velocity Feedback (DVF) perform well when the structural parameters are well known [15-17]. Linear methods such as H2, H∞ try to minimize proper norms of the transfer function of the system providing robust control with respect to the frequency of excitation [18-21].

When structural properties vary with time, the effectiveness of linear controllers is reduced and it is advisable to use control algorithms capable of adapting themselves [22-24]. In particular, the use of nonlinear/adaptive control strategies is recommended when uncertainty in structural parameters is involved, when the structure has a non-linear behaviour and when physical limits of devices must be managed.

Early research on adaptive control was motivated by the need of designing autopilots for aircrafts operating over a wide range of conditions and having nonlinear and time varying behavior [25]. Then, tracking control was adopted in the field of industrial automation for designing robots with unknown kinematic and dynamic properties [26]. Finally adaptive control was introduced also in the field of civil engineering [27] where it is particularly useful for managing nonlinear structural behavior and model uncertainties.

Recently, several reviews have been published on advances in structural control, each one focusing on a specific aspect of the general topic. Fisco and Adeli report the main studies and developments on active, semi-active and hybrid control since 1997 to 2011 [28, 29]. Korkmaz describes an overview of advances in active structural control adopting an interdisciplinary approach [30]. Amezquita-Sanchez et al. focus on reviewing the main control techniques applied to suppress vibrations in civil structures using smart actuators and sensors with special attention to technological innovations [31]. A very interesting review on structural control was published by a team of researchers members of the European Association for the Control of Structures [32]. The review reports the latest developments on each branch on the structural control, starting from passive methods to the most challenging new tendencies of adaptive control. Saaed et al. describe the state-of-the-art on structural control presenting advantages and disadvantages of each kind of approach for vibration mitigation in civil structures [33]. Although very useful to provide an overview on structural application of active control, none of the previously mentioned reviews is specifically devoted to adaptive control techniques.

The aim of the present paper is to fill this gap and present an up-to-date literature review on adaptive control approaches adopted for structural applications. In particular, the paper is devoted to provide an extensive description of the applications of adaptive control methods in the field of civil engineering. The paper is organized as follows: after an introduction provided in Section 1, a classification of adaptive methods available for structural control is provided in Section 2. Following an original approach proposed by the author, the available methods are classified on the basis of the goal they are intended to pursue in civil engineering applications. In particular, Section 3 reports control approaches handling systems with uncertain parameters, Section 4 illustrates adaptive control strategies for structures with time-varying parameters and Section 5 provides a survey on nonlinear controllers for managing physical limits of actuators. Finally, recent perspectives are briefly discussed in Section 6 and conclusions are drawn in Section 7.

2. CLASSIFICATION OF ADAPTIVE CONTROL METHODS

In adaptive control the controller's parameters adapt themselves to the controlled system, whose characteristics vary with time or are initially uncertain. Fig. (1) shows a schematic representation of the adaptive control. The adaptive algorithm provides direct estimates of the controllers parameters at each time t by processing the plant input u and output y.

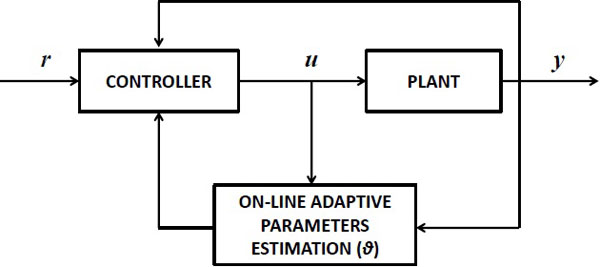
Fig. (1). Schematic of the adaptive control.

A general characterization of the adaptive control parameters θ is the following:

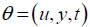(1)

The adaptive control algorithms differ for the strategy used for the parameters' adjustment.

Traditional classification divides adaptive control methods into model-based control algorithms, that require the knowledge of model parameters, and non model-based algorithms, exploiting fuzzy logic or neural networks [34, 35]. The main advantage of model-based strategies is that they allow the physical interpretation of the system behaviour and in some cases they can identify system's parameters variations. The main advantage of non model-based methods is that they can handle nonlinearity, accommodate a high degree of parallel implementation, and tolerate uncertainty in the system [36, 37].

Another separation is made between feedforward and feedback adaptive control methods. In a feedback system, the control input is computed using the error between the measured output and a reference output [38] while in a feedforward system the regulation is based on knowledge of the process or measurements of the process disturbances [39, 40].

A further common distinction is between direct and indirect adaptive control methods. Direct methods are those in which the estimated parameters are directly used in the adaptive controller. In contrast, indirect methods are those in which the estimated parameters are used to calculate required controller parameters. The estimate of the controlled parameter is treated as the true parameters (certainty equivalence).

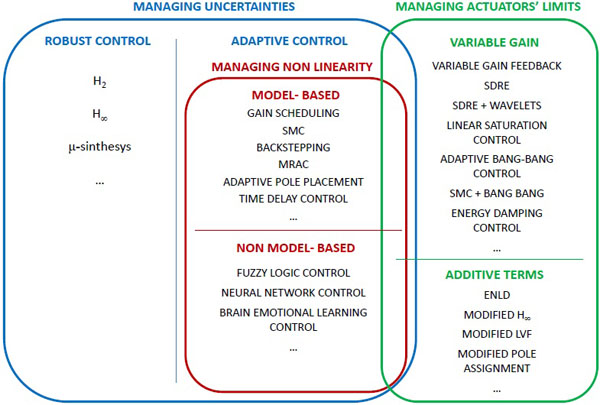
Hereinafter, in order to give a clear presentation of the literature survey, a different classification is proposed. Adaptive methods for structural control are here classified on the basis of the main goal each strategy is intended to pursue. In particular, three categories can be identified:

  1. Control strategies managing structural parameters' uncertainty;
  2. Control strategies managing system's nonlinear (time-variant) behaviour;
  3. Control strategies managing actuators' stroke and force limitations.

Fig. (2) shows the proposed classification of adaptive control methods, based on their main objective. The figure reports the three categories and for each one summarizes the most well-known approaches, presented in the following Sections 3 to 5. It is worth noticing that the adaptive control strategies usually adopted for managing structural nonlinearity can also manage model uncertainties. Moreover, in some cases there is not a sharp separation between the second and the third goals as adaptive control techniques usually used for nonlinear systems can be modified to copy with physical limits of actuators.

It must be underlined that also some fault tolerant control schemes could in principle be classified as adaptive methods. Nevertheless the treatment of this further topic is beyond the scope of the paper [41, 42].

3. CONTROL STRATEGIES COPYING WITH UNCERTAINTIES

Most civil engineering problems involve uncertainties in parameters characterizing the structure and the loads. The aim of the adoption of control systems in structural applications is to have a system behaving in the desired way, satisfying limit states requirements.

Although active control has an inherent robustness as it modulates the control force based on the states of the system, the gap between nominal and actual system's parameters may give rise to suboptimal solutions. Hence the necessity of control strategies capable of copying with parameters uncertainties.

A robust controller is a constant gain feedback algorithm that may be designed to manage parameter changes, provided that such changes are within certain bounds [43-45]. Adaptive control differs from robust control as it does not need information about the bounds of the uncertain parameters [46]. While robust control guarantees that the control strategy is effective if the parameters are within given bounds, in adaptive control the control law is changed for adapting to system's modifications [47]. Differently from adaptive control, in robust control also linear algorithms can be used.

The most widespread robust control strategy in structural applications is the H∞ approach, capable of dealing with the problem of robust stabilization and disturbance attenuation of uncertain systems. The method is based on the assumption of norm-bounded perturbations of the structure about a nominal configuration. It minimizes the H∞ norm of the transfer function of the system adopting a worst-case approach, thus leading to over-conservative results. The H2 controller analogously, minimizes the H∞ norm of the system's transfer function which represents the root mean square of the structural response to white noise excitation [48]. Among the robust control strategies, the μ-synthesis searches for a controller minimizing the Linear Fractional Transformation of the system's transfer function through a double sequential optimization [49]. New tendencies are probabilistic approaches for handling parameters' uncertainties in structural control. Guo developed an efficient reliability method for robust control of dynamic systems with probabilistic parametric uncertainties. Robust control design is carried out by solving a reliability-based optimization problem where the disturbance attenuation and control cost are minimized under the condition that reliability requirement is satisfied [50].

Fig. (2). Classification of adaptive control methods.

4. ADAPTIVE CONTROLLERS FOR NONLINEAR STRUCTURES

Most civil structures are considered having a linear behaviour in normal operating conditions. However it is well known that flexible structures like long span bridges, tall buildings, towers and cables, can experience under severe loading a significant nonlinear behaviour. Nonlinear response can also be due to damage or to deterioration with time.

For structures with nonlinear behaviour, the adoption of linear active control strategies leads to unsatisfactory results. In this case it is necessary to recur to adaptive methods that can manage the changing of structural properties with time. Several adaptive solutions for active and semi-active control devices have been proposed [51-53].

The following subsections are devoted to present an overview of the main adaptive methods adopted for structural control.

4.1. Model-based Adaptive Controllers

One of the earlier approaches of model-based nonlinear control is gain scheduling. The basic idea of gain scheduling is to design the controller for different operating points, i.e. different parameters of the nonlinear system. For each operating point, a feedback controller with constant gain is designed to meet performance requirements for the corresponding linear model. This leads to a controller whose gain is time-dependent and is obtained by interpolating over the set of gains covering the operating points [54-56].

As rapid changes of the controller gains may lead to instability, the gain variation speed must be limited. Moreover, as the adjustment mechanism of the controller gains is computed off-line, variations in the structure dynamics may lead to deterioration of performance.

Most model based adaptive algorithms are based on the concept that the system, although its parameters vary with time, should exhibit a desired response. The controller is designed in order to lead the structure close to the target behaviour. When designing adaptive control systems, special consideration is necessary on convergence and robustness issues. Lyapunov stability is typically used to derive control adaptation laws and show convergence.

The Sliding mode control belongs to this class of algorithms [57]. A sliding surface is generated consisting of a linear combination of state variables and controllers, designed to drive the response trajectory on to the sliding surface based on the Lyapunov stability criterion [58, 59]. The algorithm provides discontinuous control forces, forcing the closed-loop system to evolve in a sliding mode along a sliding or switching surface, chosen in the state-space. This can yield insensitivity to plant parameters variations. Drawbacks are the choice of the switching surface, the chattering associated to the sliding modes and the required measurement of all the state variables.

Backstepping is a recursive control algorithm for stabilizing highly nonlinear dynamic systems [60]. In order to have the output following a certain reference signal, the error signal is used to rewrite the equation of motion and a control Lyapunov function is used to derive the virtual control. The adaptive backstepping control has been mostly used in structural applications for active base isolation [61-64] and for regulating semi-active devices [65-67]. Just a few applications have been developed for active mass dampers [68].

The Model reference adaptive control is based on the definition of a reference model of the structure and the performance requirements, describing the desired I/O properties of the closed-loop system [69]. Usually, the Lyapunov equation is used to define the adaptation law, based on a quadratic Lyapunov function candidate. The controller guarantees that for any given reference input, the tracking error which represents the deviation of the response from the desired target, converges to zero with time. A few example of structural applications for structures under earthquakes are available in literature [70-73].

Adaptive pole placement control originates from the pole placement control used in the case of LTI systems with known parameters, that tries to place the poles of the closed-loop transfer function at the desired positions. In case of unknown parameters, certainty equivalence approach is used to replace the unknown vector with its estimate. The linear quadratic design technique or frequency domain design techniques can be used to design the control. Adaptive pole placement controllers are often referred to as self-tuning regulators. A recent structural application of adaptive pole placement control was developed for beams equipped with piezoelectric actuators [74]. A wavelet-based adaptive pole placement was recently proposed in which the optimum values of the closed-loop poles of the structural system are changed adaptively, based on the energy content over frequency evaluated with the discrete wavelet transform [75]. Another variation of a linear strategy is the adaptive H∞ algorithm that manages not only disturbances but also system's faults [76]. With this aim an adaptive stabilizing term is added, based on Lyapunov theory.

Time delay control algorithm calculates the control input by estimating approximately uncertain parameters from the information in a few previous time steps [77, 78]. A reference model is adopted to define the desired trajectory. TDC has the features of being simple and having excellent robustness to unknown system dynamics and disturbances. It is particularly useful for systems with dynamics slowly changing, like structures subjected to time degradation.

4.2. Non Model-based Adaptive Controllers

In recent years, non model-based techniques have gained large attention as they do not require knowledge of the structural system and therefore can handle nonlinearity and system's uncertainty. Compared to the classical control theories, they are more versatile and flexible although they do not provide optimal control.

Among non model-based control strategies, methods based on fuzzy logic are the most diffused. They are based on fuzzy logic, in which logic variables vary continuously between 0 and 1, in contrast to the classic digital logic. In fuzzy logic control the control signal is regulated by a collection of if-then rules. The main advantage of fuzzy control is that it can be expressed in terms that human operators can understand. The typical fuzzy logic control scheme is comprised of a fuzzifier (transforming signals to fuzzy variables), a reasoning module (generating fuzzy inferences) and a defuzzifier (converting fuzzy outcomes into proper signals). Many recent structural applications of fuzzy logic control can be found in literature. Al-Dawod et al. adopted fuzzy controllers for the mitigation of the vibrations of benchmark buildings equipped with AMD, showing numerically and experimentally the good performance of the controller [35, 79, 80]. Faravelli et al. discussed how to build an adaptive fuzzy controller capable of detecting system modifications and react properly, also in case of systems fault [81]. Other authors proposed the application of fuzzy logic control for ATMD on tall buildings [82-85]. Many authors investigated the adoption of fuzzy control for structures subjected to earthquake [86-89].

Another kind of non-model based controllers are neural networks controllers exploiting artificial neural networks. Their main advantage is the ability to learn on-line with no a priori training. Neural networks are composed of simple elements inspired by biological nervous systems. The neural network can be trained to perform a particular task, so that a particular input leads to a specific target output. Most of the existing studies in structural control using neural networks require computationally intensive off-line training. The advantages of on-line adaptation are demonstrated using the controller's capability to handle actuator failures and system uncertainties [41]. Many structural applications exists in which conventional controllers are trained by neural networks in order to reduce the response of buildings under earthquake excitations [90-93].

Some applications of neuro-fuzzy control for semi-active devices have been developed, in which the neural networks are adopted to compensate for time-delay and the fuzzy controller is used to determine the control current to be applied to MR dampers [94-96]. Other learning systems, like brain emotional learning control have been recently proposed. The BELC is a strategy which imitates judgment and emotion of a brain. It contains two neural networks (sensory and emotional) that affect each other thus improving the approximation ability for nonlinear systems [97].

5. CONTROLLERS FOR CONSTRAINED SYSTEMS

In case of extreme loading conditions, such as wind storms and strong earthquakes, the control devices can be forced to operate close to their physical limits, such as maximum stroke extension and force saturation of the actuator. The consequence is the application of an impulsive force that can provoke damage to the control device or to the structure. Even when damage can be prevented by brake systems and buffers that soften the impulse loads, the overall control effectiveness can be impaired or the system can operate in an anomalous way that might produce instability [98].

A proper way to handle physical limits of active control devices providing acceptable solutions from an economic viewpoint, is including them directly in the control law, allowing the system to reach its limits in a controlled way [98, 99], adopting nonlinear control strategies [100]. Nonlinear controllers proposed in the last years for constrained systems can be classified in two main groups. The first group, collects linear control strategies whose gain is updated on-line, depending on the states of the system. The second group gather together methods in which nonlinear terms are included in the expression of the control law to modulate the control signal in proximity of the physical boundaries of the system. In the following Sections 5.1 and 5.2, approaches belonging to the two categories are presented.

5.1. Control Strategies with State-dependent Variable Gain

5.1.1. Approaches Based on LQR Criterion

Many variable gain approaches are based on the Linear Quadratic Regulator criterion in which gain is updated on-line, depending on the states of the system. Within this framework, Nagashima and Shinozaki [101, 102] proposed to chose the gain among a set of feedback gains depending on an auxiliary variable that indicates a compromise between reducing the building response and reducing the stroke of the auxiliary mass. The set of gains are preliminarily computed by LQR as a function of the auxiliary parameter, allowing to keep the mass stroke below its limit. Indrawan et al. [103] developed the bounded-force control method which excludes the control-effort penalty from the perfor-mance index of LQR control and searches for optimal control force at discrete time steps. Another modification of the classical LQR method, adoptable in order to manage force and stroke limits, is the state-dependent Riccati equation approach (SDRE), a very effective tool for designing nonlinear state controllers for constrained systems [104, 105]. Methods based on the SDRE consist of solving in real-time the LQR problem with adaptive weights and system matrices [106]. This class of methods allows to fully account for system nonlinearities and to use state-dependent control weights to penalize the state variables when approaching their physical limits. Though very effective in theory, the SDRE has the main issues of being computationally demanding and of requiring the use of a state observer [107, 108], which practically limit its applications. As a modification of SDRE technique, Basu and Nagarajaiah [109] used wavelets for estimating the instantaneous frequency content of the seismic input and to adapt the control weights consequently. Materazzi and Ubertini [110] applied SDRE to systems with both stroke limit and actuators saturation. In order to fully exploit actuator's capacity, Kim and Jabbari proposed a state feedback control law using state observation in which control performance depended on the actuator's capacity [111].

5.1.2. Approaches Based on Bang-bang Control Law

Another class of algorithms able to inherently embrace the problem of actuators saturation are those based on bang-bang control law. The bang-bang control, which minimizes a performance index subjected to the control force constraint, has the main shortcoming of the undesirable chattering near the origin of the state space that is due to high frequency switching of the control force [112]. In order to tackle this issue, Mongkol et al. [113] proposed the linear saturation (LS) control approach that consisted of a low-gain linear control when the system was close to the zero state and a bang-bang control elsewhere. Wu and Soong [114] introduced the suboptimal bang-bang control, where the feedback control force was obtained by minimizing the time derivative of a quadratic Lyapunov function under the saturation constraint. This method was found effective under certain conditions but could become unstable outside eliminate of a certain range of values of the control force. To avoid this instability, Lim et al. [115-117] proposed an adaptive bang-bang control algorithm, where the stability is guaranteed by changing the value of a parameter proportional to the term which determines the direction of control force. All the aforementioned algorithms based on bang-bang control law guarantee only stability for nominal LTI systems and do not consider uncertainties in systems' parameters. To overcome this problem, Cai et al. [118] proposed the modified sliding-mode bang-bang control method based on a combination of the sliding-mode control (SMC) and the modified bang-bang control methods. Lee et al. [119] presented the saturated SMC method based on SMC theory and proved it to be an effective method for vibration control in civil building structures, although robustness of the SMC with respect to uncertainties in systems' parameters was only guaranteed in the sliding mode. Park and Min [100] addressed the stochastic nature of the excitation proposing a nonlinear control algorithm, called energy damping control, for SDOF systems subjected to random excitations. The joint probability density function of the closed-loop system was derived and used to evaluate the bound of the control force that limited the probability of limit crossing of the displacement to a prescribed value.

5.2. Approaches Based on Additive Terms

Another group of adaptive methods for managing physical limits of active control systems comprehends methods based on modifying the control law with additive terms devoted to slow down the actuators in proximity of their limits. In Chase et al. [120]. a modification of the H∞ control strategy is presented where a state-dependent non-linear term depending on the state of the system is added, capable of modeling of actuators' saturation and dealing with parameters' uncertainties. Diaz and Reynolds [121] proposed the on-off non linear velocity feedback control capable of dealing with significant levels of vibration and force saturation. To feedback the acceleration, a first-order compensator is designed in order to achieve stability and significant damping. The proposed control scheme is completed by a nonlinear element to account for actuator overloading. Yamamoto e Sone [122] proposed to modulate the feedback obtained by pole assignment method by a coefficient representing the activity of the AMD and depending on the stroke displacement and the time derivative of the first modal displacement estimated by a Kalman filter. Venanzi et al. [123, 124] recently proposed an enhanced non-linear damping (ENLD) approach for AMDs, capable of solving the issue of a limited stroke extension and force saturation. The ENLD method is a skyhook control algorithm complemented by a non-linear breaking term that becomes effective in the vicinity of the stroke limit and a modulation term that is activated close to the control force limit. The main features of the ENLD strategy lie in its ease of implementation, owing to its collocated nature, in its reduced computational time and in the unnecessity of state observers that may induce error and time delay.

6. RECENT PERSPECTIVES

Nowadays the concept of “smart structures”, is spreading in the scientific community to denote structures equipped with active control systems and monitoring sensors. Actuators allow the reduction of structural vibrations while sensors have the double function of providing feedback information to the control system and provide information useful for structural identification and health monitoring. Vibration control and health monitoring have been actively investigated in last decades but in most of the researches the two aspects have been treated separately. In recent years, some authors proposed integrated procedures for identification, control and damage detection in structures. Gattulli and Romeo [125] proposed an integrated procedure for adaptive vibration control and damage detection. The control algorithm is based on a model reference and sliding mode control and the on-line identification is based on tracking error. The convergence of the estimation process is assured by modifying the estimated parameters by a Lyapunov-based adaptation law. Adaptive control techniques are also exploited by Wrobleski and Yang [126] to identify the transfer function of simplified models, knowing measurements of input forces and output displacements. In two companion papers by Xu and Chen [127, 128] is presented a methodology for integrated vibration control and health monitoring of building structures equipped with semi-active friction dampers. A model updating scheme based on adding a known stiffness by semi-active fiction dampers is proposed and used for damage detection. The Model-reference adaptive identification algorithm, proposed by Chu and Lo [129], exploits the scheme of MRAC based on the definition of an actual target structure, whose response is known by measurement, and a numerical model, whose parameters must be adapted to fit experimental data. Chen et al. [130] presented a general approach in the time domain for integrated control and on-line damage detection adaptable to various types of control devices. A parameter identification scheme is developed to identify structural stiffness parameters and update the model which is used to regulate the controllers. In Yang et al. the health monitoring is based on substructuring the floor's response and estimating the stiffness change while the vibration control is based on model reference adaptive control [131]. Xu et al. presented a real-time integrated procedure to identify time-varying structural parameters and unknown excitation and to control building's vibration [132]. The identification is based on the least-square estimation method and the measures input - output information and the vibration control is based on the clipped optimal control and updated parameters.

Structural resilience is another emerging research field in civil engineering. In this context, adaptive control systems can be very useful as they are able to adapt themselves to changing levels of loading and even to changing structural configurations (damaged, undamaged) becoming a proper means to improve structural resilience. Domaneschi and Martinelli evaluated resilience of seismic control solutions for cable-stayed bridges by proposing a strategy for recovering the optimal configuration of the controlled bridge after a damaging event [133].

Another interesting potential development of adaptive control concerns the possibility of designing structures with changing shape characteristics, like buildings with adaptive envelopes and bridges with adaptive cross section [134-136]. The adaptive façade of a tall building can potentially control the vortex shedding phenomenon and in addition provide natural ventilation and energy efficiency to the structural system. Adaptive wind turbines could optimize at the same time the structural performance and the energy transformation. A bridge deck adaptable to the external actions of wind can ensure aerodynamic stability and reduce internal forces and vibration.

Although several potential applications of adaptive methods can be recognized in structural engineering, several issues still discourage the practical implementation in real systems. A well-known drawback of standard adaptive control techniques is the possible instability that could occur in case of non-perfect system-model error cancelation, due to unmatched uncertainties, unmodelled actuator dynamics, high frequency neglected modes and time delays. These problems can be mitigated through the adoption of robust adaptive control modifications of the basic approaches like σ-modification, e-modification and parameter’s projection [24]. In these techniques specific modifications are applied to the adaptation law in order to avoid the drift of the controller's parameters that could induce actuator saturation and closed loop instability.

Moreover, the necessity of robustness in case of lack of power supply encourages the adoption of adaptive hybrid or semiactive control devices instead of purely active systems [9, 65, 90]. For this reason, large effort was recently made towards the improvement of semiactive devices and towards embedding control algorithms in their analytical formulation [137, 138].

The opportunity currently offered by many research laboratories to physically test adaptive systems (in parallel to numerical tests) [17, 66, 72] and the development of electric actuators capable of providing large control forces with reduced delays [122], potentially will soon allow to bridge the gap between theory and practice and to increase practical applications of adaptive structural control.

CONCLUSION

An up-to-date survey on adaptive methods for structural control is presented in this paper. While in the last decades most effort was devoted to the development and the application of robust control methods capable of dealing with uncertainties, more recently adaptive control methods capable of self-modifications started to be investigated in civil engineering. The main applications of adaptive control are for buildings subjected to seismic events that can experience parameters variations due to damage, for structures subjected to multiple hazards, requiring different levels of damping depending on loading conditions and for structures experiencing nonlinear behaviour like cables, slender towers and bridges. Another important branch of the research was recently devoted to avoid actuators' saturation and stroke limits crossing through modification of control strategies.

Future developments of adaptive control can address, among others, interdisciplinary applications like: i) integration of active control and structural health monitoring of deteriorating structures; ii) structural shape adaptation for the double purpose of energetic efficiency improvement and vibration control. The spreading opportunity of physically testing adaptive control systems and the fast technological developments in the field of smart systems, will soon allow the increase of real applications of adaptive systems for structural control.

CONFLICT OF INTEREST

The author confirms that this article content has no conflict of interest.

ACKNOWLEDGEMENTS

Declared none.

REFERENCES

1 T. Soong, Active Structural Control Theory and Practice., Longman Scientific & Technical: Essex, England, 1990. 2 A.K. Dutta, S.K. Deb, and A. Dutta, "Design of an active controller for Quincy Bayview Bridge, Illinois, U.S.A. against seismic excitation - part II: Control implementation", Struct. Control Health Monit., vol. 15, pp. 1078-1104, 2008.
[CrossRef Link] 3 H. Xu, C. Zhang, H. Li, P. Tan, J.P. Ou, and F.L. Zhou, "Active mass driver control system for suppressing wind-induced vibration of the Canton Tower", Smart Struct. Syst., vol. 13, pp. 281-303, 2014.
[CrossRef Link] 4 C. Li, and J. Zhang, "Investigations of vibration control of tall buildings under wind loads using active tuned mass damper", J. Earthq. Eng. Eng. Vib., vol. 27, pp. 160-165, 2007. 5 Y. Ikeda, "Active and semi-active vibration control of buildings in Japan - practical applications and verifications", Struct. Control Health Monit., vol. 16, pp. 703-723, 2009.
[CrossRef Link] 6 J. Teng, H. Xing, C. Liu, H. Li, and J. Ou, "Design and implementation of AMD system for response control in tall buildings", Smart Struct. Syst., vol. 13, pp. 235-255, 2014.
[CrossRef Link] 7 F. Casciati, G. Magonette, and F. Marazzi, Technology of Semiactive Devices and Applications in Vibration Mitigation., Wiley: Hoboken, USA, 2006.
[CrossRef Link] 8 F. Casciati, and M. Domaneschi, "Semi-active electro-inductive devices: Characterization and modelling", J. Vib. Control, vol. 13, pp. 815-838, 2007.
[CrossRef Link] 9 V. Gattulli, M. Lepidi, and F. Potenza, "Seismic protection of frame structures via semi-active control: Modeling and implementation issues", Earthq. Eng. Eng. Vib., vol. 8, pp. 627-645, 2010.
[CrossRef Link] 10 N. Rahbari, and S. Talatahari, "On the efficiency of semi-active smart structures: self-regulating MR dampers control system for tall buildings", Struct. Des. Tall. Spec., vol. 23, pp. 1027-1044, 2014.
[CrossRef Link] 11 B. Spencer, S. Dyke, and H. Deoskar, "Benchmark problems in structural control: part II active tendon system", Earthq. Eng. Struct. Dyn., vol. 27, pp. 1141-1147, 1998.
[CrossRef Link] 12 H. Garrido, O. Curadelli, and D. Ambrosini, "Semi-active friction tendons for vibration control of space structures", J. Sound Vib., vol. 333, pp. 5657-5679, 2014.
[CrossRef Link] 13 C. Chang, B. Spencer, and P. Shi, "Multiaxial active isolation for seismic protection of buildings", Struct. Control Health Monit., vol. 21, pp. 484-502, 2014.
[CrossRef Link] 14 H. Li, and J. Ou, "A design approach for semi-active and smart base-isolated buildings", Struct. Control Health Monit., vol. 13, pp. 660-681, 2006.
[CrossRef Link] 15 S. Bhattacharyya, A. Datta, and L. Keel, Linear Control Theory: Structure Robustness and Optimization., CRC Press: USA, 2009. 16 Y. Kim, K. You, and J. You, "Active control of alongwind response of a tall building with AMD using LQR controller", Appl. Mech. Mater., vol. 490-491, pp. 1063-1067, 2014.
[CrossRef Link] 17 F. Ubertini, I. Venanzi, and G. Comanducci, "Considerations on the implementation and modeling of an active mass driver with electric torsional servomotor", Mech. Syst. Signal Process., vol. 58, pp. 53-69, 2015.
[CrossRef Link] 18 F. Jabbari, W. Schmitendorf, and J. Yang, "H∞ control for seismic-excited buildings with acceleration feedback", J. Eng. Mech., vol. 121, pp. 994-1002, 1995.
[CrossRef Link] 19 J.B. Burl, Linear Optimal Control., Prentice Hall: USA, 1998. 20 S. Park, J. Lee, H. Jung, D. Jang, and S. Kim, "Numerical and experimental investigation of control performance of active mass damper system to high-rise building in use", Wind Struct., vol. 12, pp. 313-332, 2009.
[CrossRef Link] 21 Y. Wang, J. Lynch, and K. Law, "Decentralized h∞ controller design for large-scale civil structures", Earthq. Eng. Struct. Dynam., vol. 38, pp. 377-401, 2009.
[CrossRef Link] 22 K.J. Astrom, and B. Wittenmark, Adaptive Control., 2nd ed. Addison-Wesley: USA, 1995. 23 I. Landau, R. Lonzano, M. M'Saad, and A. Karimi, Adaptive Control Algorithms, Analysis and Applications., Springer-Verlag: London, 2011. 24 P. Ioannou, and J. Sun, Robust Adaptive Control., Dover Pubblications: USA, 2012. 25 E. Pallet, Automatic Flight Control., Granada Publishing: London, 1979. 26 G. Rigatos, Modelling and Control for Intelligent Industrial Systems., Springer-Verlag: Berlin Heidelberg, 2011.
[CrossRef Link] 27 R. Burdisso, L. Suarez, and C. Fuller, "Feasibility study of adaptive control of structures under seismic excitation", J. Eng. Mech., vol. 120, pp. 580-592, 1994.
[CrossRef Link] 28 N.R. Fisco, and H. Adeli, "Smart structures: Part I-Active and semi-active control", Sci. Iran A., vol. 18, no. 3, pp. 275-284, 2011.
[CrossRef Link] 29 N.R. Fisco, and H. Adeli, "Smart structures: Part II-Hybrid control systems and control strategies “", Sci. Iran A., vol. 18, no. 3, pp. 285-295, 2011.
[CrossRef Link] 30 S. Korkmaz, "A review of active structural control: challenges for engineering informatics", Comp. Struct., vol. 89, pp. 2113-2132, 2011.
[CrossRef Link] 31 J.P. Amezquita-Sanchez, A. Dominguez-Gonzalez, R. Sedaghati, R. De Jesus Romero-Troncoso, and R.A. Osornio-Rios, "Vibration control on smart civil structures: a review", Mech. Adv. Mater. Struct., vol. 21, no. 1, pp. 23-38, 2014.
[CrossRef Link] 32 B. Basu, O.S. Bursi, F. Casciati, S. Casciati, A.E. Del Grosso, M. Domaneschi, L. Faravelli, J. Holnicki-Szulc, H. Irschik, M. Krommer, M. Lepidi, A. Martelli, B. Ozturk, F. Pozo, G. Pujol, Z. Rakicevic, and J. Rodellar, "A European association for the control of structures joint perspective. Recent studies in civil structural control across Europe", Struct. Control Health Monit., vol. 21, no. 12, pp. 1414-1436, 2014.
[CrossRef Link] 33 T.E. Saaed, G. Nikolakopoulos, J-E. Jonasson, and H. Hedlund, "A state-of-the-art review of structural control systems", J. Vib. Control, vol. 21, no. 5, pp. 919-937, 2015.
[CrossRef Link] 34 G. Rigatos, "Model-based and model-free control of flexible-link robots: a comparison between representative methods", Appl. Math. Model., vol. 33, pp. 3906-3925, 2009.
[CrossRef Link] 35 M. Morlacchi, F. Resta, F. Ripamonti, and G. Tomasini, "An adaptive non-model-based control strategy for smart structures vibration suppression", In: Proceedings of SPIE, Europe, 2013.
[CrossRef Link] 36 M. Al-Dawod, B. Samali, and J. Li, "Experimental verification of an active mass driver system on a five-storey model using a fuzzy controller", Struct. Control Health Monit., vol. 13, pp. 917-943, 2006.
[CrossRef Link] 37 M. Soleymani, and M. Khodadadi, "Adaptive fuzzy controller for active tuned mass damper of a benchmark tall building subjected to seismic and wind loads", Struct. Des. Tall Spec., vol. 23, pp. 781-800, 2014.
[CrossRef Link] 38 Q. Hu, G. Ma, and L. Xie, "Robust and adaptive variable structure output feedback control of uncertain systems with input nonlinearity", Automatica., vol. 288, pp. 43-56, 2005. 39 T. Ma, and H. Yang, "Adaptive feedback-feedforward control of building structures", J. Eng. Mech., vol. 130, pp. 786-793, 2004.
[CrossRef Link] 40 J. Fei, and Y. Fang, "Robust adaptive feedforward vibration control for flexible structure", Int. J. Innov. Comput. I, vol. 6, pp. 2189-2197, 2010. 41 S. Suresh, S. Narasimhan, S. Nagarajaiah, and N. Sundararajan, "Fault-tolerant adaptive control of nonlinear base-isolated buildings using emran", Eng. Struct., vol. 32, pp. 2477-2487, 2010.
[CrossRef Link] 42 F. Weng, Y. Ding, J. Ge, L. Liang, and G. Yang, "Finite-time vibration control of earthquake excited linear structures with input time-delay and saturation", J. Low Freq. Noise V. A., vol. 33, pp. 245-270, 2014.
[CrossRef Link] 43 Y.R. Hu, and A. Ng, "Active robust vibration control of flexible structures", J. Sound Vib., vol. 288, pp. 43-56, 2005.
[CrossRef Link] 44 Y. Chen, F.D. Ulker, V. Wickramasinghe, and D.G. Zimcik, "Development of robust control law for active buffeting load alleviation of smart fin structures", J. Intell. Mater. Syst. Struct., vol. 25, pp. 818-831, 2014.
[CrossRef Link] 45 A.Y. Fallah, and T. Taghikhany, "Robust semi-active control for uncertain structures and smart dampers", Smart Struct. Syst., vol. 23, no. 095040, 2014. 46 J. Achermann, Robust Control: Systems with Uncertain Physical Parameters., Springer: New York, 1993.
[CrossRef Link] 47 K. Astrom, L. Neumann, and P. Gutman, "A comparison between robust and adaptive control of uncertain systems", In: 2nd IFAC Workshop on Adapative Systems in Control and Signal Processing, Sweden, July-3, 1986. 48 R. Conway, and R. Horowitz, "Guaranteed cost control for linear periodically time-varying systems with structured uncertainty and a generalized H2 objective", Mechatronics, vol. 20, pp. 12-19, 2010.
[CrossRef Link] 49 T. Li, and Y. Ma, "Robust vibration control of flexible tensegrity structure via μ synthesis", Struct. Control Health Monit., vol. 20, pp. 53-66, 2013.
[CrossRef Link] 50 S-X. Guo, "An efficient reliability method for probabilistic H-infinity robust control of uncertain linear dynamic systems", J. Vib. Control, vol. 21, pp. 2946-2958, 2015.
[CrossRef Link] 51 G. Pujol, L. Acho, F. Pozo, and J. Rodellar, "A nonlinear damping control for the vibration mitigation of the benchmark highway bridge", Struct. Control Health Monit., vol. 16, no. 5, pp. 586-598, 2009.
[CrossRef Link] 52 M. Domaneschi, and L. Martinelli, "Optimal passive and semi-active control of a wind excited suspension bridge", Struct. Infrastruct E., vol. 9, no. 3, pp. 242-259, 2013.
[CrossRef Link] 53 X-L. Ning, P. Tan, D-Y. Huang, and F. Zhou, "Application of adaptive fuzzy sliding mode control to a seismically excited highway bridge", Struct. Control Health Monit., vol. 16, no. 6, pp. 639-656, 2009.
[CrossRef Link] 54 E. Prempain, and I. Postlethwaite, "L2 and H2 performance analysis and gain scheduling synthesis for parameter-dependent systems", Automatica., vol. 44, pp. 2081-2089, 2008.
[CrossRef Link] 55 A. McKernan, A. Sala, C. Arino, and G.W. Irwin, "Sampled-data gain scheduling of continuous LTV plants", Automatica., vol. 45, pp. 2451-2453, 2009.
[CrossRef Link] 56 R. Korlin, S. Boonto, H. Werner, and U. Starossek, "Lmi-based gain scheduling for bridge flutter control using eccentric rotational actuators", Optim. Control Appl. Methods, vol. 33, pp. 488-500, 2012.
[CrossRef Link] 57 V. Utkin, "Variable structure system with sliding modes", IEEE Trans. Automat. Contr., vol. 22, pp. 212-222, 1977.
[CrossRef Link] 58 J. Yang, J. Wu, and A. Agrawal, "Sliding mode control for seismically excited linear structures", J. Eng. Mech., vol. 121, pp. 1386-1390, 1995.
[CrossRef Link] 59 E. Matheu, and M. Singh, "Output-feedback sliding-mode control with generalized sliding surface for civil structures under earthquake excitation", Earthq. Eng. Struct. Dynam., vol. 27, pp. 259-282, 1998.
[CrossRef Link] 60 F. Ikhouane, and M. Krstc, "Robustness of the tuning functions adaptive backstepping design for linear systems", IEEE Trans. Automat. Contr., vol. 43, pp. 431-437, 1998.
[CrossRef Link] 61 P. Liu, K-Y. Lian, and C-S. Chiu, "Adaptive robust control for seismically excited structures: the chi-chi earthquake", Zhongguo Gongcheng Xuekan, vol. 25, pp. 403-414, 2002.
[CrossRef Link] 62 V. Manosa, F. Ikhouane, and J. Rodellar, "Control of uncertain non-linear systems via adaptive backstepping", J. Sound Vibrat., vol. 280, pp. 657-680, 2005.
[CrossRef Link] 63 F. Pozo, F. Ikhouane, G. Pujol, and J. Rodellar, "Adaptive backstepping control of hysteretic base-isolated structures", J. Vib. Control, vol. 14, pp. 373-394, 2006.
[CrossRef Link] 64 C.Z. Wen, and W. Cai, "Adaptive control of a base isolated system for protection of building structures", J. Vib. Acoust., vol. 128, pp. 261-268, 2005. 65 M. Zapateiro, H. Karimi, N. Luo, B. Phillips, and B. Spencer Jr, "Semiactive backstepping control for vibration reduction in a structure with magnetorheological damper subject to seismic motions", J. Intell. Mater. Syst. Struct., vol. 20, pp. 2037-2053, 2009.
[CrossRef Link] 66 M. Zapateiro, H. Karimi, N. Luo, and B. Spencer Jr, "Real-time hybrid testing of semiactive control strategies for vibration reduction in a structure with MR damper", Struct. Control Health Monit., vol. 17, pp. 427-451, 2010. 67 M. Zapateiro, H. Karimi, and N. Luo, "Semiactive vibration control of nonlinear structures through adaptive backstepping techniques with h∞ performance", Int. J. Syst. Sci., vol. 42, pp. 853-861, 2011.
[CrossRef Link] 68 Y. Hacioglu, and N. Yagiz, "Adaptive backstpping control with estimation for the vibration isolation of buildings", J. Vib. Control, vol. 18, pp. 1996-2015, 2011.
[CrossRef Link] 69 L-L. Fan, and Y-D. Song, "Neuro-adaptive model-reference fault-tolerant control with application to wind turbines", IET Control Theory A, vol. 6, pp. 475-486, 2012.
[CrossRef Link] 70 K. Baba, D. Yamamoto, and M. Akagi, "Model reference adaptive control systems with state estimators to mitigate seismic responses of structures", Theor. Appl., vol. 51, pp. 123-132, 2002. 71 S-Y. Chu, S-C. Lo, and M-C. Chang, "Real-time control performance of a model-reference adaptive structural control system under earthquake excitation", Struct. Control Health Monit., vol. 17, pp. 198-217, 2010.
[CrossRef Link] 72 J. Tu, X. Lin, B. Tu, J. Xu, and D. Tan, "Simulation and experimental tests on active mass damper control system based on model reference adaptive control algorithm", J. Sound Vib., vol. 333, pp. 4826-4842, 2014.
[CrossRef Link] 73 I. Venanzi, and L. Ierimonti, "Exploiting multiple reference models for adaptive control of flexible structures", ECCOMAS Congress, 5-10 June, Greece, 2016 74 T. Zhang, and H. Li, "Adaptive pole placement control for vibration control of a smart cantilevered beam in thermal environment", J. Vib. Control, vol. 19, pp. 1460-1470, 2013.
[CrossRef Link] 75 F. Amini, and M. Samani, "A wavelet-based adaptive pole assignment method for structural control", Comput. Aided Civ. Infrastruct. Eng., vol. 29, pp. 464-477, 2014.
[CrossRef Link] 76 L. Acho, and G. Pujol, "Adaptive control design of structural systems", In: American Control Conference, 27-29 June, USA, 2012, pp. 6120-6125. 77 D. Jang, J. Park, and H. Jung, "Active mass damper system employing time delay control algorithm for vibration mitigation of building structure", Proc. SPIE, vol. 8692, p. 8692, 2013. 78 D. Jang, H. Jung, and Y. Moon, "Active mass damper system using time delay control algorithm for building structure with unknown dynamics", Smart Struct. Syst., vol. 13, pp. 305-318, 2014.
[CrossRef Link] 79 M. Al-Dawod, B. Samali, F. Naghdy, and K. Kwok, "Active control of along wind response of tall building using a fuzzy controller", Eng. Struct., vol. 23, pp. 1512-1522, 2001.
[CrossRef Link] 80 B. Samali, and M. Al-Dawod, "Performance of a five-storey benchmark model using an active tuned mass damper and a fuzzy controller", Eng. Struct., vol. 25, pp. 1597-1610, 2003.
[CrossRef Link] 81 L. Faravelli, R. Rossi, and G. Torelli, "Numerical testing of a programmable microcontroller with fuzzy and adaptive features", Simul. Model. Pract. Theory, vol. 11, pp. 421-431, 2003.
[CrossRef Link] 82 A. Ahlawat, and A. Ramaswamy, "Multiobjective optimal fuzzy logic control system for response control of wind-excited tall buildings", J. Eng. Mech., vol. 130, pp. 524-530, 2004.
[CrossRef Link] 83 H-S. Kim, and Y-W. Kang, "Active control of alongwind response of a tall building with amd using LQR controller", Eng. Struct., vol. 41, pp. 242-257, 2012.
[CrossRef Link] 84 S. Edalath, A. Kukreti, and K. Cohen, "Enhancement of a tuned mass damper for building structures using fuzzy logic", J. Vib. Control, vol. 19, pp. 1763-1772, 2013.
[CrossRef Link] 85 A. Aly, "Proposed robust tuned mass damper for response mitigation in buildings exposed to multidirectional wind", Struct. Des. Tall Spec., vol. 23, pp. 664-691, 2014.
[CrossRef Link] 86 A. Sagirli, C. Azeloglu, R. Guclu, and H. Yazici, "Self-tuning fuzzy logic control of crane structures against earthquake induced vibration", Nonlinear Dyn., vol. 64, pp. 375-384, 2011.
[CrossRef Link] 87 D. Das, T. Datta, and A. Madan, "Design of an active controller for quincy bayview bridge, illinois, U.S.A. against seismic excitation - part II: Control implementation", Earthq. Eng. Struct. Dynam., vol. 41, pp. 99-118, 2012.
[CrossRef Link] 88 N. Ahn, H-L. Bui, N-L. Vu, and D-T. Tran, "Application of hedge algebra-based fuzzy controller to active control of a structure against earthquake", Struct. Control Health Monit., vol. 20, pp. 483-495, 2013.
[CrossRef Link] 89 H. Shariatmadar, and H. Razavi, "Seismic control response of structures using an ATMD with fuzzy logic controller and pso method", Struct. Eng. Mech., vol. 51, pp. 547-564, 2014.
[CrossRef Link] 90 J. Fan, Y. Zhang, and J. Wei, "Semi-active intelligent control of sliding structure based on artificial neural network", J. Earthq. Eng. Eng. Vib., vol. 27, pp. 130-135, 2007. 91 S. Narasimhan, S. Suresh, S. Nagarajaiah, and N. Sundararajan, "On-line learning failure-tolerant neural-aided controller for earthquake excited structures", J. Eng. Mech., vol. 134, pp. 258-268, 2008.
[CrossRef Link] 92 D. Kim, "Neuro-control of fixed off-shore structures under earthquake", Eng. Struct., vol. 31, pp. 517-522, 2009.
[CrossRef Link] 93 A.K. Karamodin, and H.H. Kazemi, "Semi-active control of structures using neuro-predictive algorithm for MR dampers", Struct. Control Health Monit., vol. 17, pp. 237-253, 2010. 94 H-S. Kim, P. Roschke, P-Y. Lin, and C-H. Loh, "Neuro-fuzzy model of hybrid semi-active base isolation system with fps bearings and an MR damper", Eng. Struct., vol. 28, pp. 947-958, 2006.
[CrossRef Link] 95 Z-D. Xu, and Y-Q. Guo, "Neuro-fuzzy control strategy for earthquake-excited nonlinear magnetorheological structures", Soil. Dyn. Earthq. Eng., vol. 28, pp. 717-727, 2008.
[CrossRef Link] 96 H. Ghaffarzadeh, and V. Hamedi, Semi-Active Control of Structures Using a Combined Genetic Algorithm - Neural Network - Fuzzy Controller., vol. 93. Civil- Comp Proceedings, 2010. 97 C-M. Lim, and C-C. Chung, "Fuzzy brain emotional learning control system design for nonlinear systems", Int. J. Fuzzy Syst., vol. 17, pp. 117-128, 2015.
[CrossRef Link] 98 A. Forrai, S. Hashimoto, H. Funato, and K. Kamiyama, "Robust active vibration suppression control with constraint on the control signal: application to flexible structures", Earthq. Eng. Struct. Dynam., vol. 32, pp. 1655-1676, 2003.
[CrossRef Link] 99 A. Saberi, A. Stoorvogel, and P. Sannuti, Control of Linear Systems with Regulation and Input Constraints., Springer: London, 2000.
[CrossRef Link] 100 J. Park, and K. Min, "Bounded nonlinear stochastic control based on the probability distribution for the sdof oscillator", J. Sound Vib., vol. 281, pp. 141-153, 2005.
[CrossRef Link] 101 I. Nagashima, and Y. Shinozaki, "Variable gain feedback control technique of active mass damper and its application to hybrid structural control", Earthq. Eng. Struct. Dynam., vol. 26, pp. 815-838, 1997.
[CrossRef Link] 102 I. Nagashima, R. Maseki, Y. Asami, J. Hirai, and H. Abiru, "Performance of hybrid mass damper system applied to a 36-storey high-rise building", Earthq. Eng. Struct. Dynam., vol. 30, pp. 1615-1637, 2001.
[CrossRef Link] 103 B. Indrawan, T. Kobori, M. Sakamoto, N. Koshika, and S. Ohrui, "On-off nonlinear active control of floor vibrations", Earthq. Eng. Struct. Dynam., vol. 25, pp. 179-193, 1996.
[CrossRef Link] 104 J.R. Cloutier, "State-dependent Riccati equation techniques: An overview", American Control Conference, 6-6 June, Albuquerque, NM, U.S.A, 1997.
[CrossRef Link] 105 B. Friedland, "On controlling systems with state-variable constraints", American Control Conference, 26-26 June, Philadelphia, PA, U.S.A, 1998. 106 C. Mracek, and J. Cloutier, "Control designs for the nonlinear benchmark problem via the state-dependent Riccati equation method", Int. J. Robust Nonlin., vol. 8, pp. 401-433, 1998.
[CrossRef Link] 107 M. Hassan, "Observer-based controller for discrete-time systems: A state dependent Riccati equation approach", Nonlinear Dyn., vol. 70, pp. 693-707, 2012. 108 M. Tadi, "State-dependent Riccati equation for control of aeroelastic flutter", J. Guid. Control Dyn., vol. 26, pp. 914-917, 2003.
[CrossRef Link] 109 B. Basu, and S. Nagarajah, "A wavelet-based time-varying adaptive lqr algorithm for structural control", Eng. Struct., vol. 30, pp. 2470-2477, 2008.
[CrossRef Link] 110 A.L. Materazzi, and F. Ubertini, "Robust structural control with system constraints", Struct. Control Health Monit., vol. 19, pp. 472-490, 2012.
[CrossRef Link] 111 J. Kim, and F. Jabbari, "Actuator saturation and control design for buildings under seismic excitation", J. Eng. Mech., vol. 128, pp. 403-412, 2002.
[CrossRef Link] 112 C. Lim, T. Chung, and S. Moon, "Adaptive bang-bang control for the vibration control of structures under earthquakes", Earthq. Eng. Struct. Dynam., vol. 32, pp. 1977-1994, 2003.
[CrossRef Link] 113 J. Mongkol, B. Bhartia, and Y. Fujino, "On linear-saturation (LS) control of buildings", Earthq. Eng. Struct. Dynam., vol. 25, pp. 1353-1371, 2012.
[CrossRef Link] 114 Z. Wu, and T. Soong, "Modified bang-bang control law for structural control implementation", J. Eng. Mech., vol. 122, pp. 771-777, 1996.
[CrossRef Link] 115 C. Lim, Y. Park, and S. Moon, "Robust saturation controller for linear time invariant system with structured real parameter uncertainties", J. Sound Vib., vol. 294, pp. 1-14, 2006.
[CrossRef Link] 116 C. Lim, "Remarks on robust stability of saturation controllers", J. Sound Vib., vol. 299, pp. 363-372, 2007.
[CrossRef Link] 117 C. Lim, "Active vibration control of the linear structure with an active mass damper applying robust saturation controller", Mechatronics, vol. 18, pp. 391-399, 2008.
[CrossRef Link] 118 G. Cai, J. Huang, F. Sun, and C. Wang, "Modified sliding-mode bang-bang control for seismically excited linear structures", Earthq. Eng. Struct. Dynam., vol. 29, pp. 1647-1657, 2000.
[CrossRef Link] 119 S. Lee, K. Min, and Y. Lee, "Improved design of sliding mode control for civil structures with saturation problem", Earthq. Eng. Struct. Dynam., vol. 33, pp. 1147-1164, 2004.
[CrossRef Link] 120 J. Chase, S. Breneman, and H. Smith, "Robust h∞ static output feedback control with actuator saturation", J. Eng. Mech., vol. 125, pp. 225-233, 1999.
[CrossRef Link] 121 I. Daz, and P. Reynolds, "On-off nonlinear active control of floor vibrations", Mech. Syst. Signal Process., vol. 24, pp. 1711-1726, 2010.
[CrossRef Link] 122 M. Yamamoto, and T. Sone, "Behavior of active mass damper (AMD) installed in high-rise building during 2011 earthquake of pacific coast of Tohoku and verification of regenerating system of AMD based on monitoring", Struct. Control Health Monit., vol. 21, pp. 634-647, 2014.
[CrossRef Link] 123 I. Venanzi, and F. Ubertini, "Free vibration response of a frame structural model controlled by a nonlinear active mass driver system", Adv. Civil Eng., vol. 2014, Article ID 745814, 2014.
[CrossRef Link] 124 I. Venanzi, L. Ierimonti, and F. Ubertini, "An enhanced non-linear damping approach for handling system constraints in active mass dampers", J. Sound Vib., vol. 357, pp. 2-15, 2015.
[CrossRef Link] 125 V. Gattulli, and F. Romeo, "Integrated procedure for identification and control of MDOF structures", J. Eng. Mech., vol. 126, pp. 730-737, 2000.
[CrossRef Link] 126 M. Wrobleski, and H. Yang, "Identification of simplified models using adaptive control techniques", J. Struct. Eng., vol. 129, pp. 989-997, 2003.
[CrossRef Link] 127 Y. Xu, and B. Chen, "Integrated vibration control and health monitoring of building structures using semi-active friction dampers: Part I methodology", Eng. Struct., vol. 30, pp. 1789-1801, 2008.
[CrossRef Link] 128 Y. Xu, and B. Chen, "Integrated vibration control and health monitoring of building structures using semi-active friction dampers: Part II numerical investigation", Eng. Struct., vol. 30, pp. 573-587, 2008.
[CrossRef Link] 129 S-Y. Chu, and S-C. Lo, "Application of real-time adaptive identification technique on damage detection and structural health monitoring", Struct. Control Health Monit., vol. 16, pp. 154-177, 2009.
[CrossRef Link] 130 B. Chen, Y. Hu, and X. Zhao, "Integrated vibration control and health monitoring of building structures: a time domain approach", Smart Struct. Syst., vol. 6, pp. 811-833, 2010.
[CrossRef Link] 131 H. Yang, J. Shan, C. Randall, P. Hansma, and W. Shi, "Integration of health monitoring and control of building structures during earthquakes", J. Eng. Mech., vol. 140, no. 5, Techenical Paper 04014013, 2014.
[CrossRef Link] 132 Y. Xu, Q. Huang, Y. Xia, and H. Liu, "Integration of health monitoring and vibration control for smart building structures with time-varying structural parameters and unknown excitations", Smart Struct. Syst., vol. 15, pp. 807-830, 2015.
[CrossRef Link] 133 M. Domaneschi, and L. Martinelli, "Earthquake resilience-based control solutions for the extended benchmark cable-stayed bridge", J. Struct. Eng., vol. 142, no. 8, p. 4015009, 2016.
[CrossRef Link] 134 H. Adeli, and H. Saleh, "A Optimal control of adaptive/smart bridge structures", J. Struct. Eng., vol. 123, no. 2, pp. 218-226, 1997.
[CrossRef Link] 135 J. Hunt, W. Haase, and W. Sobek, "Designing adaptive spatial structures", J. Int. Associ. Shell Spatial Struct., vol. 49, no. 159, pp. 167-173, 2008. 136 A.E. Del Grosso, and P. Basso, "Design concepts for adaptive multi-functional building envelopes", In: Proceedings of the 6th ECCOMAS Thematic Conference on Smart Structures and Materials, Turin, Italy, 34-26 June, 2013. 137 M. Domaneschi, "Simulation of controlled hysteresis by the semi-active Bouc-Wen model", Comp. Struct., vol. 106-107, pp. 245-257, 2012.
[CrossRef Link] 138 F. Ikhouane, and J. Rodellar, Systems with Hysteresis: Analysis, Identification and Control Using the Bouc-Wen Model., John Wiley & Sons: Chichester, UK, 2007.
[CrossRef Link]