All published articles of this journal are available on ScienceDirect.
Optimal Topologies for Steel Frames with Ordinary Chevron and X-Braces: The Effect on Total Structural Cost
Abstract
Today, steel structures with simple frames and concentric steel bracings (both crossed and chevron type) are extensively used in different countries, as well as in Iran. Apart from the seismic performance of each structural system, construction cost plays a significant role in system selection by designers. In an attempt to optimize structural costs, this study aims at examining the number of floors, span length, soil conditions, and brace type. In this study the impact of these factors on structural costs are evaluated. Since parking areas are the most important architectural requirement, therefore specified span widths accommodating two, three, and four vehicles are selected for the models. To this end, regular building models with different span (5.6, 7.5, and 11.2m) are selected according to such architectural considerations. Following structural analysis and design, total structural costs are estimated according to the latest national cost list issued by the Management and Planning Organization of Iran (published in 2014). The results are obtained and reported for different models through graphs and tables. The outcomes are evaluated and compared. Finally, the optimal topologies in terms of structure weight and total cost are determined, along with introducing the most effective factor among span length, story number, brace type, and soil type.
INTRODUCTION
According to the Iranian Code of Practice for Seismic Resistant Design of Buildings [1], based on its profile and properties, soil under a structure is classified into 5 types. This classification, from hard to soft soil, is defined using experimental tests. Stone beds and strong sites are named as type I, while weak layers are named as type V. Since most of the urban sites in Iran are categorized under class II and III, in this study these classes are selected as the bases for evaluation. The main purpose of this study is to propose the most economical topology as structural system, based on the extensive evaluation of different soil types, number of floors, various span lengths, and bracing systems. These parameters play important roles in the optimization of buildings.
Among numerous investigations carried out on structural optimization, Sanaei & Babaei [2] developed an algorithm based on the cellular automata for the topology optimization of continuous structures. Lauren et al. [3] examined the optimal brace geometry of frames and proposed a method for optimal frame system design, using different ways of discrete and continuous connection for the elements. In 2014, Rahjo & Mameghani [4] examined seismic behavior of 6, 12, and 18 floor cross-braced frames with different layouts, while an earlier study by Liang et al. [5] investigated the topology optimization for multi-story steel frames and proposed the optimal topology for 6 and 12 floor frames. Zhou and Chen [6] presented a method to optimize the topology of braced frames using the method of moving asymptotes (MMA) and the steepest descent method. Pan et al. [7] worked on adding cover-plate for diagonal braced steel frames. Another study focused on the optimum placement of dissipaters in braced steel buildings subjected to the shaking-table test that were conducted by Foti [8].
The search for optimal topologies has been carried out by Babaei et al. for RC frames with and without shear walls [9, 10], for steel moment resisting frames [11], and for composite structures [12] with different ductility levels. In this work, however, the aim is to examine the effect of different topologies on the total structural cost and to propose an optimal layout for simple steels frames with concentric braces. Therefore, in this article, building models are defined similar to those investigated in the past works [9-12] to provide comparable results.
The main purpose of this study is to investigate and explore optimal topologies based on the architectural requirements. These requirements have not been applied as constraints in the literature, thus impractical layouts could be obtained in topology optimization and only a few of them would satisfy the architectural considerations and ease of construction. For this purpose, three types of arrangements for columns and beams with different storey numbers (up to 8 floors) are assumed as building models satisfying the above architectural requirements. Fig. (1) illustrates the structural plan for the models. These models are similar to those structures studied in the literature to obtain the best topology for reinforced concrete moment resisting frames, steel moment resisting frames, and composite structures by Babaei et al. [10-12].
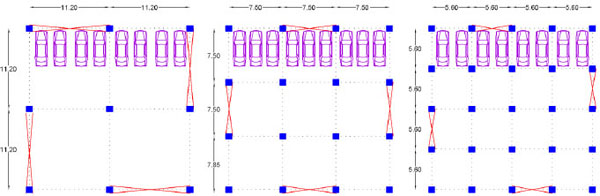
METHODOLOGY
In this study, 24 structural models are considered: 12 models are built in soil type II and 12 models in soil type III, with span lengths 5.6 m, 7.5 m, and 11.2 m. Models have five and eight floors. Two types of bracings, X-type and chevron configuration, are considered to resist lateral loads. The structural system of all building models consists of simple steel frame with X-shape or chevron concentric braces and all national and international design regulations and considerations are employed for this system. Loads consist of 200, 100, and 100 kg/m2 for live load of floors, live load of roofs, and uniformly distributed equivalent live load of partitions respectively. A Uniform dead load of 700 kg/m2 is applied in all floors.
The selected span lengths and the space between columns, which are 5.6 m, 7.5 m, and 11.2 m, are calculated based on the architectural requirements to place two, three, and four vehicles, respectively, between columns. Reinforcement bars of 4000 kg/cm2 yield strength and concrete type C30 of 30 MPa compression strength are employed for foundation design. All models are designed according to the Iranian [13, 14] and American [15] codes and requirements. Regular structural building models with approximately 23 m×23 m plan dimensions (an area of about 530 square meters) are considered. Fig. (1) displays the plan and the position of chevron and X braces layout.
According to the Iranian Code of Practice for Seismic Resistant Design of Buildings (2005) [1], based on its profile and properties, the soil where a structure is built is classified into five types, type I to V. Stone beds and semi-stone layers are the strongest sites, categorized as type I, while soil layers decrease in strength and stiffness as approaching type V. The soil classification is determined using experimental tests. Most of the urban sites in Iran are in the class of II and III, so these classes are selected for evaluation in this study.
As previously mentioned, based on the majority of geological properties in the urban sites of Iran, soil types II and III are taken into consideration for evaluation. The properties of the models are defined in this section. The coefficient of structural behavior is R=5, basic acceleration is assumed to be A=0.35, building importance factor is I=1, and the height of all floors is set to be H=3.5 m. The buildings are considered to be built in Tehran. Study procedure and methodology is as follows: in the first step, structural elements and foundation are designed using conventional design procedures followed by changing the element sections based on the design experience of the authors and a trial and error procedure, satisfying convergence criteria. Subsequently, structural design sheets are drawn, and cost of all structural elements, roofs, foundation, excavation, form work and reinforcement steels are estimated based on the latest national cost list, which has been published in 2014 by the Management and Planning Organization of Iran. The results are presented and compared through a series of figures and graphs.
RESULTS
Building models are analyzed and designed. Columns, beams and bracings are grouped similarly in models to obtain comparable results. Structural costs are estimated based on the required reinforcement and concrete for foundations, the required materials for the composite roofs, and the required steel for beams, columns and braces.
Figs. (2-13) represent the results, showing the required materials and their total costs. It is concluded that the total structural cost of models with five floors and X-braces in soil type II are 22% less than that of the models with chevron braces. Furthermore, X-braces are shown to be 10% more economical than the chevron types in soil type III. Eight-story structures with X-braces are 2% and 1.5% more economical than chevron braces in soil types II and III, respectively. Five-story structures with X-braces in soil type II are 2% more cost-effective than the eight-story buildings in the same soil type, whereas five-story buildings with chevron braces in soil type III are shown to be 10% lower in total cost than eight-story structures with the same brace and soil type.
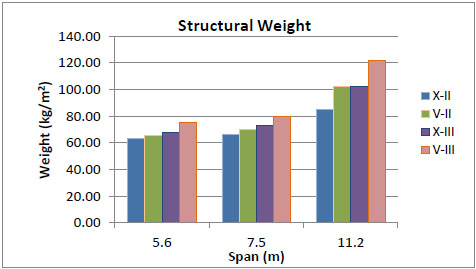
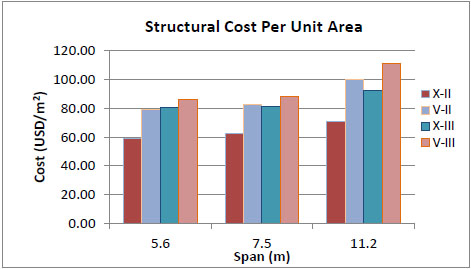
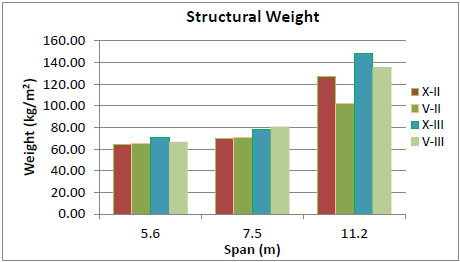
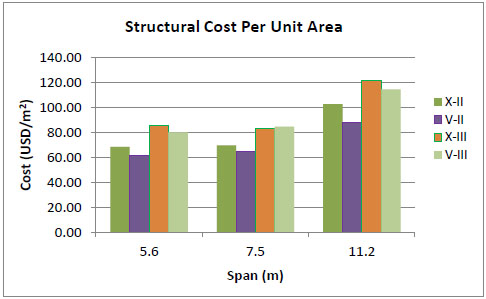
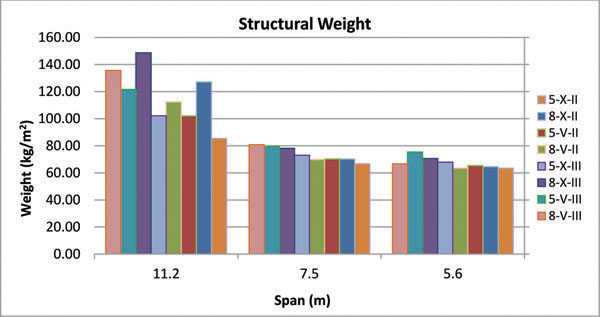
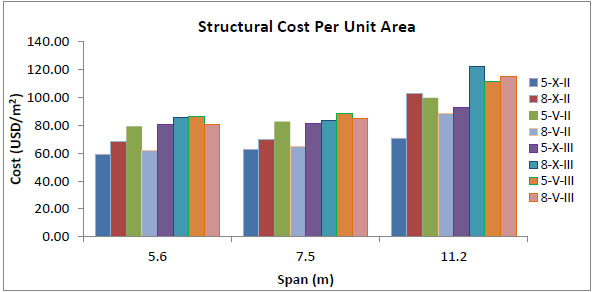
Figs. (8-13) represent the total structural cost versus story number for all models. The intersection point in every figure shows a specific story number in which both bracing types have the same cost. As shown in the figures, for buildings with considerably smaller or larger spans, X-bracing system is economic only for 7-story buildings while for buildings with mid-range spans the most favorable is the 6-story model. In general, the intersection points refer to 6 and 7-story buildings, so that chevron-type is more economic for taller buildings while buildings with shorter structures would benefit from the X-type.
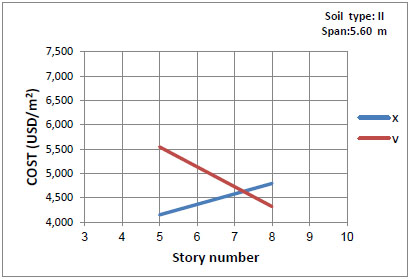
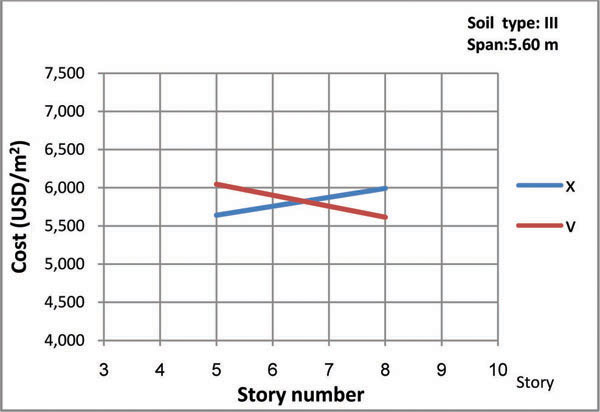
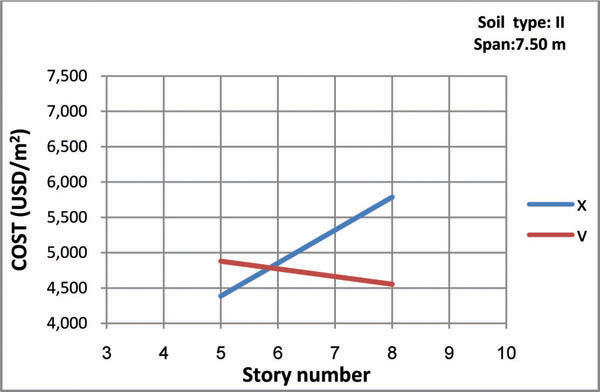
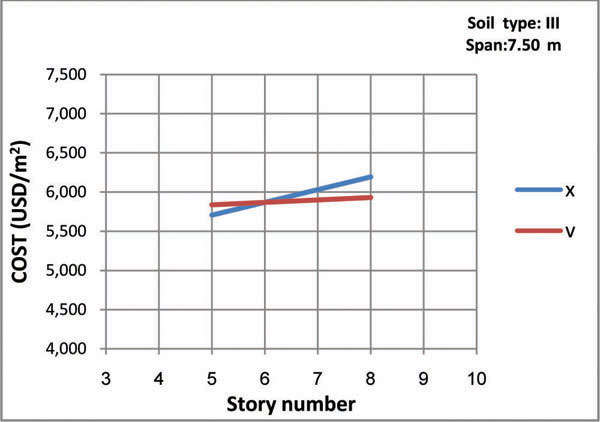
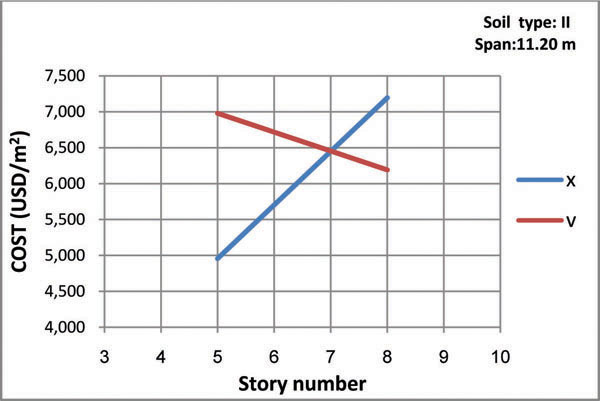
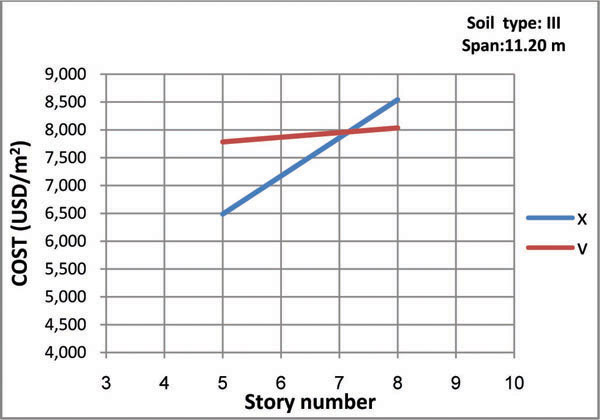
Table 1 proposes an optimal span (distance between columns) for buildings with different story numbers and different brace types. Additionally, Table 2 presents a comparison of the total cost between different brace types.
| ID | Number of Stories | Soil Type | Brace Type | Optimal span | ||
|---|---|---|---|---|---|---|
| 5.6 | 7.5 | 11.2 | ||||
| 1 | 5 | II | X | ● | ||
| 2 | III | ● | ||||
| 3 | 5 | II | chevron | ● | ||
| 4 | III | ● | ||||
| 5 | 8 | II | X | ● | ||
| 6 | III | ● | ||||
| 7 | 8 | II | chevron | ● | ||
| 8 | III | ● | ||||
| ID | Number of stories | Soil Type | Bracing Type | |
|---|---|---|---|---|
| X | Chevron | |||
| 1 | 5 | II | 79% | 100% |
| 2 | III | 92% | 100% | |
| 3 | 8 | II | 100% | 88% |
| 4 | III | 100% | 94% | |
CONCLUSION
In the current study, simple steel frame structures with concentric braces (X type and chevron) are investigated by examining 24 models and the results are presented in graphs and tables. The outcomes of this study are as follow:
- Employing chevron braces for structures with span of 5.6 m built in soil type II and III is optimal for buildings with more than six and seven floors, respectively.
- Using chevron braces for structures with span of 7.5 m built in soil type II and III is optimal for buildings with more than six floors.
- Chevron braces for structures with span of 11.2 m built in soil type II and III are optimal for buildings with more than seven floors.
- In general, chevron bracing is economic for taller buildings and X-type is ideal for shorter structures, based on the properties of the models defined in this study.
- Results for structures with more than eight floors may be different than those reported in this study; therefore, further research is needed to determine reliable results.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
Declared none.


