All published articles of this journal are available on ScienceDirect.
Fractal Characteristic Analysis of Watershed as Variable of Synthetic Unit Hydrograph Model
Abstract
Fractal characteristic of watershed is an important parameter which influences the formation of synthetic unit hydrograph. Based on a previous study, hydrology response of watershed expressed in hydrograph form could be well presented by hydrology network characteristic as a form of fractal characteristic of watershed [1]. Fractal characteristic of watershed was stated as fractal dimension which was presented in three parameters i.e. river branch ratio (RB), river length ratio (RL) and watershed river area ratio (RA). The purpose of this research was to analyze fractal characteristic and to verify its fractal dimension stability as preliminary research to prepare variables which would be used to develop synthetic unit hydrograph model in the future. Analysis was undertaken using two methods i.e. Horton’s Coefficient Ratio and Box Counting Dimension. Analysis result revealed that fractal dimension of river network from 8 watersheds calculated using those two methods could give almost the same result, ranged from 1 to 2. Fractal dimension from calculation also showed similarity with study conducted by Tarboton et al. [2], Balkhanov et al. [3], Khanbabaei et al. [4], obtaining that fractal dimension of river network is generally in the range of 1 to 2.
1. INTRODUCTION
Synthetic unit hydrograph (SUH) is a rainfall-runoff transformation model developed based on watershed characteristic. This watershed characteristic is related with morphometric characteristic as primary parameter to build hydrograph model such as watershed area (A), main river length (L), main river gradient (S) and other parameters. Besides being based on morphometric characteristic, synthetic unit hydrograph can be developed based on dimensionless unit hydrograph such as SCS unit hydrograph and conceptual model of watershed reservoir, such as Clark, Nash and Geomorphological Unit Hydrograph (GUH).
In recent study, development of synthetic unit hydrograph model can be based on fractal characteristic of watershed. Fractal characteristic of watershed is part of morphometric parameter particularly related directly to network characteristic of river hydrology. An interesting point to be noticed in this fractal concept implementation is that watershed hydrology response can be very well presented by characteristic of hydrology network as a form of watershed fractal characteristic [1]. SUH modelling using watershed fractal characteristic especially based on conceptual modelling has been studied by some researchers such as Rodriguez-Iturbe et al. who introduced geomorphologic instantaneous unit hydrograph concept in 1979 [5-7]. Furthermore, in 1997 Duchesne et al. developed a synthetic unit hydrograph model named as Hydrogramme Unitaire Universel (H2U) [8]. In relation to this SUH development, the first step needs to be carried out is determining parameter that will become model variable based on watershed fractal characteristic. This analysis can be conducted using 2 methods i.e. Horton’s Coefficient Ratio and Box Counting Dimension.
Analysis of fractal characteristic of watershed has been widely performed in foreign countries watershed, especially in the United States and Europe, while in Indonesia is relatively rarely performed and only limited in Java Island as conducted by Kartiwa et al. in 2003 [9] and Kusumayudha et al. in 2015 [10]. Indonesia as an archipelagic region has typical characteristic of watershed which are dominated by small watershed area with short river profile. Therefore, this research is very important especially to analyze fractal characteristic and to verify its fractal dimension stability with the goals to prepare variables which would be used to develop synthetic unit hydrograph model in the future in Indonesia especially in Central Sulawesi Province .
2. MATERIAL AND METHODS
2.1. Watershed Description
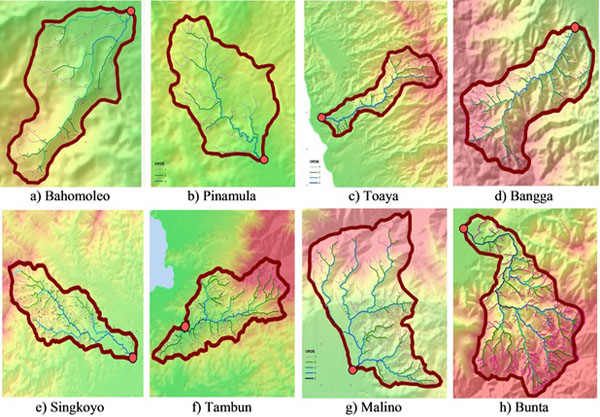
This research was conducted at 8 watersheds in Central Sulawesi Province, Indonesia as presented in Fig. (1). The name of these watershed are Bahomoleo, Pinamula, Toaya, Bangga, Singkoyo, Tambun, Malino, Bunta. Based on topography map observation, these watershed are situated at elevation ranging between 50 m to 1700 meters above sea level and are dominated by steep (45% to 65%) and very steep (> 65%) surface slope. The topography of the watershed is a mountain with various valleys and miscellaneous stream.
The eight watersheds used as samples in this research involve an area around 23.88 km2 to 144.73 km2 as shown in Fig. (2) and Table 1, and all of them included in the category in meso scale watershed (10 km2<Area<1000 km2) based on classification written by Stefan et al. [11, 12]. In general, the average river slope of these watersheds are above 3%, included in the category of steep river compared to river slope in Java and Borneo islands, which reflect the type of mountain rivers in Sulawesi Island. However, if they were further observed, river slope varied according to their segments. In upstream, generally river slope tended to be very steep, in middle segment it had moderate slope whereas in downstream segment it had low gradient. Therefore, the influence of ocean tides to the river flow was hardly found because downstream had a positive gradient.
| Watershed | Watershed Area (A, km2) | Main River Length (L, m) | Main River Gradient (S) | Watershed Form Factor (FB) |
|---|---|---|---|---|
| Bahomoleo | 23.88 | 10315.36 | 0.07639 | 0.30 |
| Pinamula | 49.35 | 15636.28 | 0.03422 | 0.39 |
| Toaya | 65.51 | 21817.08 | 0.06532 | 0.21 |
| Bangga | 68.19 | 16484.77 | 0.08948 | 0.37 |
| Singkoyo | 116.05 | 26810.29 | 0.04569 | 0.22 |
| Tambun | 118.19 | 19990.61 | 0.09755 | 0.50 |
| Malino | 128.75 | 19192.51 | 0.10812 | 0.49 |
| Bunta | 144.73 | 28699.57 | 0.06359 | 0.36 |
As shown in Table 1, the eight watersheds also had various form factor (FB). The highest watershed form factor was possessed by Tambun Watershed with a value of 0.50 which depicted similarity of watershed form with circular form with form factor of 0.754 for complete circular [13].
2.2. Fractal Characteristic of Watershed
Fractal theory developed from self-similarity concept between system total size (fraction) and its smallest size (fractal). Study development of fractal was initiated by Mandelbrot [14, 15], who exhibited theory of fractal geometry as self-similarity unit from an object. Mandelbrot [14] stated that each natural object acted as fractal, in this matter, was as a result of the same force which worked on various level of an object so that it resulted in iteration or repetition of basic form (fractal seed or fractal generator), which was its result unit was in the object concerned. This process was well known as self-similarity process which behaved as scale invariant, meaning that even it was observed using various scales, its both geometric size and dimension was the same with its fractal seed. Stacey [16] described fractal as form regular pattern hidden in chaos. Mandelbrot [14] expressed regularity as accumulation of its parts in accordance with sequence of some observation scales which always followed a quadratic function law or non-linear law, so that fractal object was characterized by its dimension which was always fraction number. This fractal geometry has been used in almost all areas even in social science, economy or in arts [17].
In the hydrology science context, various studies proved that river network system was fractal, meaning that small watershed as part of (sub watershed) watershed which was larger. They statistically possess structure similarity with larger watersheds as illustrated in Fig. (3). In general the form of fractal geometry was stated in dimension (DF), describing that comparison between river bank ratio (RB) and river length ratio (RL) were generated from river order. Fractal dimension was often called Hausdorff-Besicovitch dimension. Moreover, many studies show that the fractal dimensions can be used to model the hydrologic response of a river basin through the fractal instantaneous unit hydrograph [18].
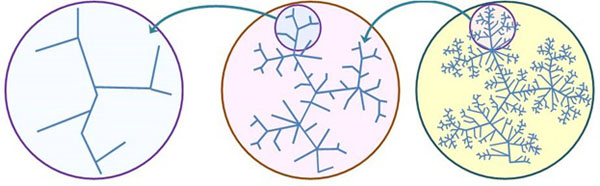
Watershed fractal dimension could be seen from two aspects i.e. organization of river hydrology network in various scales and water flow in hydrology network [2]. Fractal characteristic of river hydrology network was always constant even of it was identified with different scales and water flow resulted in water discharge was convolution product of rainfall to absorption function of its hydrology network. Fractal dimension of main river generally ranges from 1.2 to 1.4 and fractal dimension of river hydrology network generally ranges from 1.4 to 1.7 [1]. As has been mentioned by Torboton, Rosso and Gupta [1] and based on analysis result of rivers in United States of America and Europe indicated that river hydrology network had a stable fractal characteristic wherever and whenever it was. Therefore, watershed hydrology response was the function of its fractal characteristic.
As an essential part of watershed system related to transformation process of rain-discharge, organization of river network was quantitatively expressed with three parameters i.e. river branch ratio (bifurcation ratio, RB), river length ratio (length ratio, RL), and large ratio catchment area (area ratio, RA) based quantitative expression of Horton’s Law [20]. These three parameters were associated by La Barbera and Rosso [18, 21], as fractal dimension parameters.
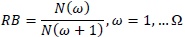 |
(1) |
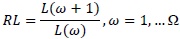 |
(2) |
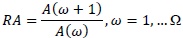 |
(3) |
RB: river bank ratio, RL: river length ratio, RA: watershed area ratio,ω: river order and
Analysis of fractal characteristic of watershed was based on topography data in this case Topographical Map of Indonesia (RBI) or data from Digital Elevation Model (DEM) with adequate resolution. DEM data was converted from Shuttle Radar Topographic Mission (SRTM) data, similar to the method used by Owusu [22], to complete objects (contour line, river network and other objects) on Topographical Map of Indonesia which was covered by cloud or unrecorded. Each variable was calculated or measured based on watershed feature which was studied using Geographic Information System (GIS) in this case Arc GIS 10, including point, line, and polygon. Point feature represented position of hydrology and hydrometric tools, line feature described river length or river segment and object whereas polygon feature depicted watershed or sub watershed area. These features measurement were carried out using Editor or Toolbox facility available in Arc GIS. The use of GIS had proven to give more accurate analysis result and more efficient time usage connected to analysis of watershed characteristic. This is also proven by Viji et al. who identified saturation areas and their locations in the river catchment with the use of Geographical Information System (GIS) and geo statistical tools of grid-based approach of land surface [23].
When data on topographical map was unclear due to cloud or other factors, data correction could be done using SRTM data. Based on this data processing result, fractal characteristic and watershed morphometric parameters i.e. fractal parameters (RB, RL, RA and D) and watershed morphometric (A, L, S, and FB) could be analyzed.
2.3. Fractal Dimension
Fractal Dimension of eight watershed can be analyzed using Horton’s Coefficient Ratio and Box Counting Dimension. Based on the first method, Horton and Stahler’s concept of river network organization has a uniformity with fractal theory scheme, where bifurcation ratio (RB) and river length ratio (RL) aforementioned revealed self-similarity from river network system which tended to be similar with fractal dimension. By employing theory of Horton, La Barbera and Rosso [21] a formula stating relationship between Horton’s parameter (RB and RL) and fractal dimension (DF) from river network could be developed based on some samples of rivers which got fractal dimension between 1.0 to 2.0 which is stated as:
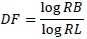 |
(4) |
The second method, fractal dimension can be calculated by using other methods such as Divider Method and Box Counting Dimension. Divider Method was used for the first time by Richardson [18] to count fractal dimension of shore line and then used by other researchers such as Snow and Montgomery [18] to determine fractal dimension of other natural objects. Box Counting Dimension was graphically developed using DEM data of watershed and then calculated using below equation:
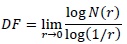 |
(5) |
N(r) is number of box covering river network and r is box size. Calculation procedure N(r) is repeated until box size is closed to 0 then is plotted in log-log graphic to obtain fractal dimension as gradient of line on log-log graphic.
3. RESULT AND DISCUSSION
3.1. Horton’s Coefficient Ratio
Fractal characteristic of watershed, as has been discussed, was described by configuration of river network (main river) and its tributaries based on stream order system in accordance with Stahler [13]. The eight watersheds studied had river order 3 to 5, with detailed information: one watershed had order 3, four watersheds had order 4, and three watersheds had order 5, as indicated in Fig. (2). Based on these orders it could be decided that the number of river segment and river length could represent fractal characteristic of each watershed as shown in Table 2 & 3. Based on these tables, tendency of decreasing number of segment was along with increasing river order. However, it did not work for river length, which showed no tendency of relation between river order and the number of river length.
| Watershed | N(1) | N(2) | N(3) | N(4) | N(5) |
|---|---|---|---|---|---|
| Bahomoleo | 34 | 15 | 14 | 3 | - |
| Pinamula | 34 | 21 | 13 | - | - |
| Toaya | 67 | 29 | 17 | 20 | - |
| Bangga | 92 | 37 | 23 | 24 | - |
| Singkoyo | 106 | 54 | 28 | 19 | - |
| Tambun | 125 | 69 | 18 | 17 | 8 |
| Malino | 137 | 62 | 51 | 10 | 2 |
| Bunta | 182 | 80 | 43 | 27 | 19 |
| Watershed | L(1) | L(2) | L(3) | L(4) | L(5) |
|---|---|---|---|---|---|
| Bahomoleo | 593.38 | 604.48 | 758.91 | 1063.24 | - |
| Pinamula | 1083.77 | 634.60 | 932.31 | - | - |
| Toaya | 730.75 | 564.35 | 469.01 | 782.21 | - |
| Bangga | 748.91 | 557.97 | 650.38 | 518.84 | - |
| Singkoyo | 725.11 | 574.45 | 621.05 | 1021.85 | - |
| Tambun | 983.45 | 700.91 | 714.78 | 604.31 | 619.01 |
| Malino | 866.37 | 540.18 | 839.62 | 986.89 | 807.11 |
| Bunta | 621.71 | 610.75 | 610.75 | 763.92 | 991.88 |
When dots of river order and segment number had conformity and depicted in graphical chart as illustrated in Fig. (4) it showed that decreasing segment number was along with increasing river order and followed exponential curve (1/EXP). It worked on all watersheds studied though curve bend is each watershed was different. The result of this study automatically supported and verified the same studies in other watersheds as reported by Kouli et al. [24], Rao et al. [25] and Paul et al. [26].
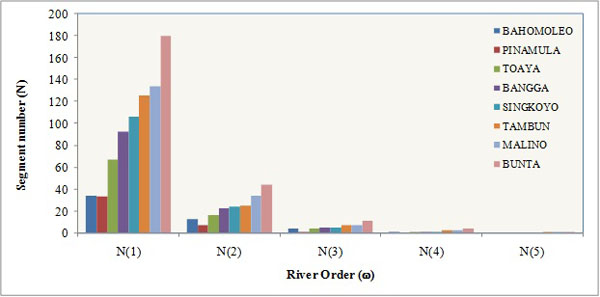
When river order and segment number were illustrated in a separated graphic for each watershed, relationship between segment number (N) representing ordinate (y) and river order (ω) representing abscissa (x) could be obtained. Value of abscissa variable was stated in normal form whereas the value of ordinate variable was stated in logarithmic form. The relation of these two variables was relatively good and expressed in linear regression form with coefficient of determination above 0.75.
Some researchers analogized that configuration of river network was similar as a tree with some branches and twigs. Main river or main stream acted as trunk and tributaries acted as branches. Some twigs met constructing branch, and some branches made trunk and finally they made a tree.
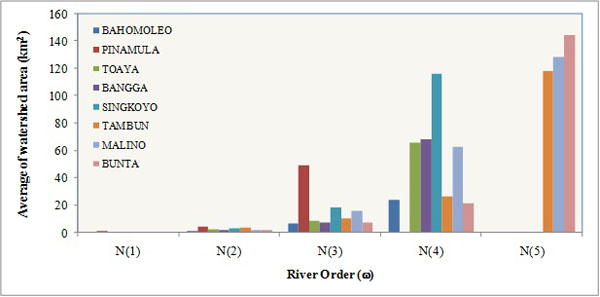
Furthermore, sub watershed areas were determined based on each river order i.e. order 1 to 5. Sub watershed areas of eight watersheds were concluded based on topography and were calculated on each order. Ideally, sub watershed area on each order was completely counted employing geographic information-based equipment i.e. Watershed Delineation Tool on Arc GIS software. However, as topographic data in form of contours and DEM had low resolution, this analysis was combined with manual digitations to correct deviation of sub watershed delineation which was activated by computer. Based on correction result, area of each watershed on each order with average area could be further decided. Following procedure implemented on segment number based on order, increment relation of average watershed area could be noticed along with increment of river order. This relationship showed contradiction with curve of segment number and river order, and it followed exponential form as shown in Fig. (5).
When each watershed was made graphic respectively to depict relationship of the two variables, linear relationship could be noticed by converting logarithm on variable of average sub watershed area. As graphic of segment number and order, relationship between variable of average sub watershed area and river order also performed good correlation. It was categorized very well with determination coefficient above 0.95. Certainly, this result was similar with that of previous researchers, where relationship between segment number and river order worked.
However, it was essential to observe that basically higher sub watershed area on order could be smaller or bigger relying on the number of previous sub watershed on order. This phenomenon could be clarified because river segment on order i-1could directly empty into (meet) on order i+1, so that number of sub watershed area on order i smaller than that of order i-1. Therefore, describing relationship between average sub watershed area and river order was more essential than describing relationship between number of sub watershed area and river order.
As has been mentioned before, river branch ratio (RB) was property dimension influenced by watershed drainage system. In general, river bank value was closely related with hydrograph form produced. Hydrograph form would be steeper on rise side and on down side along with the increment of river branch value [26] or on the other hand. Some researchers gave different references. For natural rivers, Chow [27] gave river branch value range on 2 to 5. Other researchers conveyed limit of river branch value range 3 to 5, as have been discussed by Kouli et al. [24], Rao et al. [25] and Paul et al. [26].
.
RB value for each order of the eight observed watersheds including RB average value is illustrated in Table 4. If referred to ranges of RB value as have been exposed by Pareta et al. [13], Rodriguez-Iturbe et al. [20] and Chow [27], RB value of each watershed was slightly different with range between 0.85 to 5.10. However this range could give information that rivers studied on some orders had lower RB value on upstream segment than on its downstream segment on higher order. This means that drainage in upstream segment had lower density on higher order, and it could take place on each watershed completely depending on system configuration of watershed drainage.
| Watershed | RB(1) | RB(2) | RB(3) | RB(4) | Average |
|---|---|---|---|---|---|
| Bahomoleo | 2.27 | 1.07 | 4.67 | - | 2.67 |
| Pinamula | 1.62 | 1.75 | - | - | 1.68 |
| Toaya | 2.31 | 1.71 | 0.85 | - | 1.62 |
| Bangga | 2.49 | 1.61 | 0.96 | - | 1.68 |
| Singkoyo | 1.96 | 1.93 | 1.47 | - | 1.79 |
| Tambun | 1.81 | 3.83 | 1.06 | 2.13 | 2.21 |
| Malino | 2.21 | 1.22 | 5.10 | 5.00 | 3.38 |
| Bunta | 2.28 | 1.86 | 1.59 | 1.42 | 1.79 |
Basically, river length ratio could influence peak dischage (QP) and peak time (TP) as had been proposed by Rodriguez-Iturbe et al. [20], where RL value was linearly proportional with peak discharge and inversely proportional with peak time. For natural rivers, RB value range between 1.5 to 3.5 [27]. RL value for eight (8) watersheds was on 0.59 to 1.67 as presented in Table 5, slightly different with that range.
| Watershed | RL(1) | RL(2) | RL(3) | RL(4) | Average |
|---|---|---|---|---|---|
| Bahomoleo | 1.02 | 1.26 | 1.40 | - | 1.23 |
| Pinamula | 0.59 | 1.47 | - | - | 1.03 |
| Toaya | 0.77 | 0.83 | 1.67 | - | 1.09 |
| Bangga | 0.75 | 1.17 | 0.80 | - | 0.90 |
| Singkoyo | 0.79 | 1.08 | 1.65 | - | 1.17 |
| Tambun | 0.71 | 1.02 | 0.85 | 1.02 | 0.90 |
| Malino | 0.62 | 1.55 | 1.18 | 0.82 | 1.04 |
| Bunta | 0.98 | 1.00 | 1.56 | 1.30 | 1.13 |
Furthermore, watershed area ratio (RA) was predicted to be able to influence time to attain peak discharge [27], where RA value was inversely proportional with TP. As presented in Table 6, it is clear that watershed area ratio of each sub watershed varies on each order and generally it does not show their relationship with decreasing or increasing river order.
| Watershed | RA(1) | RA(2) | RA(3) | RA(4) | Average |
|---|---|---|---|---|---|
| Bahomoleo | 3.20 | 5.67 | 3.79 | - | 4.22 |
| Pinamula | 4.49 | 10.84 | - | - | 7.67 |
| Toaya | 4.73 | 3.78 | 7.88 | - | 5.46 |
| Bangga | 3.30 | 5.23 | 9.28 | - | 5.94 |
| Singkoyo | 4.91 | 6.49 | 6.32 | - | 5.91 |
| Tambun | 5.99 | 3.11 | 2.48 | 4.49 | 4.02 |
| Malino | 4.11 | 8.14 | 4.08 | 2.05 | 4.62 |
| Bunta | 4.79 | 3.87 | 3.07 | 6.74 | 4.61 |
The above three parameters (RB, RL, and RA) state that statistic distribution of river network is based on Horton’s Law which is very essential to comprehend fractal structure of river network as shown in Table 7. In addition to the above three parameters, there is one parameter related to river network i.e. density of river network or drainage density (D) so that this parameter is assumed to have relationship with fractal characteristic of watershed. Based on the classification of river network density as mentioned by Ratnayake [28], the whole watershed in the study area met the criteria as low density of river network (D<2 km/km2). The low density of river network showed a typical watershed in Indonesia, especially in Central Sulawesi Province. The density of river network (drainage) was predicted to influence drainage flow rates in watershed surface, where drainage rate was linearly proportional with river network density, meaning that the more density of river network, the faster process of drainage flow, so that QP would be bigger and TP became shorter.
| Watershed | River Network Density (D) | Average Ratio of River Branch (RB) | Average Ratio of River Length (RL) | Average Ratio of Watershed Area (RA) |
|---|---|---|---|---|
| Bahomoleo | 1.80 | 2.67 | 1.23 | 4.22 |
| Pinamula | 1.24 | 1.68 | 1.03 | 7.67 |
| Toaya | 1.36 | 1.62 | 1.09 | 5.46 |
| Bangga | 1.72 | 1.68 | 0.90 | 5.94 |
| Singkoyo | 1.25 | 1.79 | 1.17 | 5.91 |
| Tambun | 1.69 | 2.21 | 0.90 | 4.02 |
| Malino | 1.60 | 3.38 | 1.04 | 4.62 |
| Bunta | 1.54 | 1.79 | 1.16 | 4.61 |
Fractal dimension of river network was calculated based on proportional logarithm of the total ratio of river branch (RB) with logarithm of total ratio of river length (RL) as stated in Table 8. The analysis result revealed that fractal dimension of river network from eight watersheds counted showed a similarity with study conducted by Tarboton et al. [2], Balkhanov et al. [3], Khanbabaei et al. [4], obtaining that fractal dimension of river network is generally in the range of 1 to 2. It showed that fractal dimension of various form and size of watershed was relatively constant, indicating that river hydrology network had a stable fractal characteristic for various places and time [1].
| Watershed | Total Ratio of River Branch (RB) | Total Ratio of River Length (RL) | Fractal Dimension (DF) |
|---|---|---|---|
| Bahomoleo | 8.00 | 3.68 | 1.60 |
| Pinamula | 3.37 | 2.05 | 1.69 |
| Toaya | 4.87 | 3.27 | 1.34 |
| Bangga | 5.05 | 2.71 | 1.63 |
| Singkoyo | 5.37 | 3.52 | 1.34 |
| Tambun | 8.83 | 3.60 | 1.70 |
| Malino | 13.53 | 4.17 | 1.82 |
| Bunta | 7.15 | 4.64 | 1.28 |
3.2. Box Counting Dimension
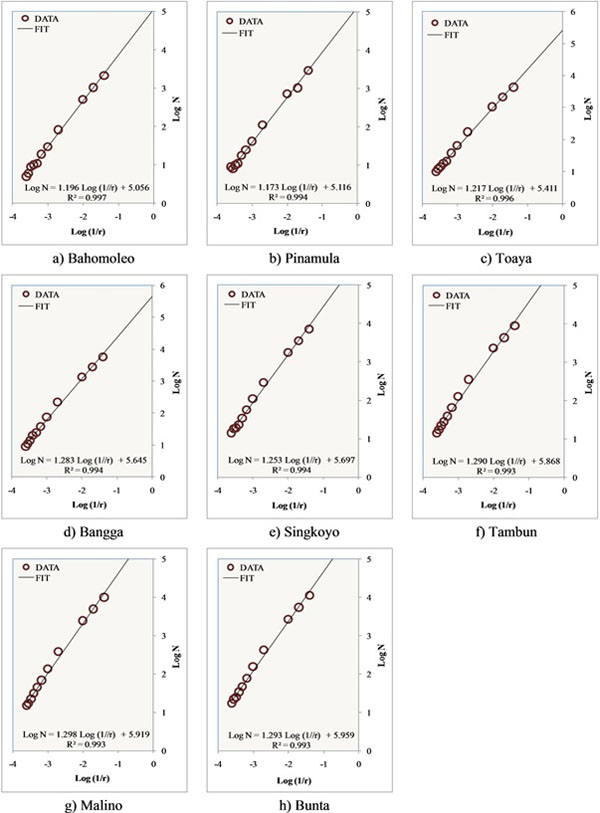
The method of Box Counting Dimension was developed to accommodate calculation which could not be counted using Eq. 4, in this case for branchless rivers or non-tributary rivers mainly river segments in upstream watershed. Analysis was executed in all watersheds studied. By using this method, relationship between box numbers and their sizes could be made based on box calculation in Fig. (6), then they were used to graphically determine fractal dimension as shown in Fig. (7).
Fractal dimension of each watershed is the gradient of regression line. For example in Fig. (7a), the equation of the regression line is Log (N)=1.196 Log (1/r) + 0.056 with determination coefficient of 0.997 . The gradient of regression line of the equation is 1.196, so that the fractal dimension of the watershed is 1.196. By using the same way, fractal dimension for other watersheds can be determined. The fractal dimension of 8 watersheds using Box Counting Dimension Method are presented in Table 9.
| Watershed | Fractal Dimension (DF) | Determination Coefficient |
|---|---|---|
| Bahomoleo | 1.196 | 0.997 |
| Pinamula | 1.173 | 0.994 |
| Toaya | 1.217 | 0.996 |
| Bangga | 1.283 | 0.994 |
| Singkoyo | 1.253 | 0.994 |
| Tambun | 1.290 | 0.993 |
| Malino | 1.298 | 0.993 |
| Bunta | 1.293 | 0.993 |
As presented in Table 9, Fractal dimension using Box Counting Dimension showed smaller value than fractal dimension using Horton’s Coefficient Ratio. However, fractal dimension in Table 9 showed similarity with fractal dimension of watershed in Table 8, range from 1 to 2, indicating that fractal dimension of eight watersheds studied were statistically stable, as stated by Irianto [1] for various watersheds researched. References have been found which state that one method is more accurate than other methods. However, both methods are widely used by researchers to analyze the fractal characteristics of watershed, to evaluate the stability of watershed fractal dimension for any purposes.
CONCLUSION
The result of analysis showed that fractal dimension of river network of eight watersheds calculated using Horton’s Coefficient Ratio and Box Counting Dimension gave almost the same result, i.e. in the range of 1 to 2. No references have been found which state that one method is more accurate than the other methods. However, both methods are widely used by researchers to analyze the fractal characteristics of watershed. Fractal dimension from calculation also showed similarity with study conducted by Tarboton et al. [2], Balkhanov et al. [3], Khanbabaei et al. [4], obtaining that fractal dimension of river network is generally in the range of 1 to 2. This also verified the previous research that river hydrology network had a stable fractal characteristic for various places and time [1] especially for watershed in Indonesia. To get more accurate results, the verification can be conducted by using other watershed in any area in Indonesia. Furthermore, the fractal characteristics of watershed expressed in three parameters (RB, RL and RA) meeting the dimensional stability, would be used as variables to develop synthetic unit hydrograph model in the next research.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
This article is part of doctoral research in Civil Engineering Department, Sepuluh Nopember Institute of Technology (ITS) Surabaya. Author thanks to Ministry of Research, Technology and Higher Education which support with BPPDN Scholarship


