All published articles of this journal are available on ScienceDirect.
Optimal Construction Scheme for Controlling Construction Errors of a Cable-strut Tensile Structure
Abstract
In a real cable-strut tensile structure, construction errors are inevitable. To explore the optimal construction scheme and control construction errors, this study optimized the construction scheme of a cable-strut tensile structure. First, a mathematical model of the element length error was investigated based on stochastic theory. By combining the balance equation, geometric equation and physical equation, the fundamental relationship between the pre-stress deviation and element length error was derived. Because the pre-stress in the active cable can be controlled exactly and the cable’s pre-stress deviations were zero during construction, the relationship between the pre-stress deviation of a passive cable and the element length error was obtained. Then, the statistical characteristics of the pre-stress deviation were obtained under different construction schemes using statistical theory. Finally, an example was analysed as a case study. The study showed that different elements have different error sensitivities and that different construction schemes have different error effects. Using the method proposed in this paper, the error effect of different construction schemes can be analysed, and the optimal construction scheme, with lower error effects and lower construction costs, can be selected for actual construction projects.
1. INTRODUCTION
A cable-strut tensile structure is a type of flexible structure composed of cables that are in tension and struts that are in compression. Because of the high strength and the adjustable stiffness distribution of the tension cables, the cable-strut tensile structure possesses excellent bearing capacity. Well-known tensile structures include the Olympic gymnastics hall in Seoul, the Redbird Arena and the Georgia Dome in the United States, the La Plata Stadium in Argentina, the Tao-Yuan County Arena in Taiwan, the Kuala Lumpur Stadium in Malaysia, the Shenzhen Baoan Stadium and the Foshan Century Lotus Stadium in China. Cable-strut tensile structures have excellent bearing capacity not only because of the high strength of the tension cables and the adjustable stiffness distribution due to the pre-stress but also by making full use of the pre-stress in providing stiffness and conserving the material. Therefore, an accurate pre-stress distribution can guarantee superior bearing performance. At the same time, the pre-stress of the structure is zero before construction and will increase along with the construction process, achieving the final pre-stress with the completion of construction. Thus, the validity and rationality of the construction technique determine the accuracy of the pre-stress distribution, meaning that the construction techniques play an important role in the pre-stress distribution.
Over the last two decades, considerable work on the construction techniques of cable-strut tensile structures has been reported. First, this construction technique was integrated into the construction scheme, and many construction schemes were investigated [1, 2], such as pretensioning the diagonal cables from outside to inside, only pretensioning the outer diagonal cable, adjusting the length of the struts from outside to inside, only adjusting the length of the outer struts, pretensioning the hoop cables from outside to inside, and only pretensioning the outer hoop cables. Second, the construction technique was combined with form-finding methods for different equilibrium states during the whole construction procedure. Before the completion of construction, due to the lack of self-stress, the assembly was slack and several methods of so-called form-finding were involved, such as the finite element method [3, 4], the dynamic relaxation method [2, 5]and the force density method [6-8]. Although those construction techniques could help to complete the construction, most of them assumed ideal conditions that ignored construction errors. However, due to the complicated working conditions, construction errors, such as element length error, installation deviation error, pin hole machining error, node or anchorage size error and temperature deviation error, are inevitable in a cable-strut tensile structure. As a result, the actual parameters of a cable-strut tensile structure, such as the pre-stress, may deviate from the ideal ones [9, 10]. Previous studies have shown that the bearing capacity of a cable-strut tensile structure is very sensitive to the pre-stress deviation [11, 12]. It is therefore necessary to evaluate the effects of construction errors and to eliminate or reduce their negative effects. Over the last ten years, many error sensitivity analysis studies had been reported [11-16]. The methods proposed by these studies are mainly divided into two types. The first type of method is established based on the probability theory, which models the errors using a group of stochastic errors conforming to a certain distribution. The second type of method is an orthogonal design method that simulates the errors with groups of deviation levels. The error sensitivity analysis can then be conducted by evaluating their effects on the distribution of the initial pre-stress and the static and dynamic structural behaviours. The construction errors that conform to not only a certain distribution but also the mathematical statistics law have not yet been studied. Similarly, although the construction techniques have been extensively investigated, most of the studies were carried out in ideal conditions that ignore construction errors. Because construction errors inevitably exist in real cable-strut tensile structures, it is necessary and important to evaluate construction error effects under different construction schemes. Moreover, selecting the optimal construction scheme with the lowest error effects is also very important for real structures. However, these studies have not yet been reported.
In this paper, a mathematical model of the element length error, which is an important construction error, was investigated based on stochastic theory. By combining the balance equation, geometric equation and physical equation, the fundamental relationship between the pre-stress deviation and element length error was derived. Next, the relationship between the pre-stress deviation of a passive cable and the element length error was obtained based on exactly controlling the active cable pre-stress. Then, the statistical characteristics of the pre-stress deviation were obtained under different construction schemes using statistical theory. Finally, an example was analysed as a case study. This study showed that different elements have different error sensitivities and that different construction schemes have different error effects. Using the method proposed in this paper, the error effect of different construction schemes can be analysed, and the optimal construction scheme, with the lowest error effects and lowest construction costs, can be selected for real construction.
2. THEORETICAL ANALYSIS
2.1. Mathematical Model of the Element Length Error
Among all the construction errors, the element length error is an important construction error and was taken as the main variable. The element length error is mainly due to original length calculation errors and machining errors. The original length calculation error is the deviation between the approximate curve equation and the real shape. In addition, temperature or humidity changes, material property changes and other factors may also contribute to element length errors. In this study, it is assumed that the errors are independent of each other and that the probability of positive or negative errors are equal. According to the Lindberg-Levy central limit theorem, the total length error obeys the normal distribution N~(µ, σ2), where µ is the average error and σ2 is the error variance. Assuming that the element length error falls in the range of [a, b], then:
 |
(1) |
where a and b are the upper and lower limits of the length error, respectively. According to the technical specifications for a cable structure (JGJ257-2012), the manufacturing errors of a cable-strut tensile structure are shown in Table 1. Using Eq. 1, the average values and standard deviations of the cable and strut length deviation distributions can be obtained, as shown in Table 2.
| Element | Element length L(m) | The allowable deviation ∆L(mm) |
|---|---|---|
| Cable | ≤50 | ±15 |
| 50<L≤100 | ±20 | |
| >100 | L/5000 | |
| Strut | ≤5 | ±5 |
| 5<L≤10 | ±10 | |
| >10 | ±15 |
| Element | Length L (m) | Average µ(mm) | Standard deviation σ(mm) |
|---|---|---|---|
| Cable | ≤50 | 0 | 5 |
| 50<L≤100 | 0 | 6.67 | |
| >100 | 0 | L/15000 | |
| Strut | ≤5 | 0 | 1.67 |
| 5<L≤10 | 0 | 3.33 | |
| >10 | 0 | 5 |
2.2. Error Sensitivity Analysis Method
To explore the construction scheme that can effectively control and reduce construction errors, the relationship between the element length change and the element internal force change was established to evaluate the error effects caused by the element length error, such as pre-stress deviation and shape deviation. In a cable-strut tensile structure, assuming that the element number is b, the node number is n, the support constraint node number is c, the following equilibrium equation (Eq. 2) [17, 18], physical equation (Eq. 3) and geometric equation (Eq. 4) can be established.
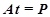 |
(2) |
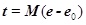 |
(3) |
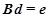 |
(4) |
where t is the internal force vector (b×1), P is the nodal load vector ((3n-c)×1), d is the node displacement vector ((3n-c)×1), e is the member expansion (b×1), e0 is the initial member expansion (b×1), M is the element stiffness matrix (b×b), and Mii=EiAi/li, where Ei, Ai, and li are the elastic modulus, section areas and lengths for element i, A is the equilibrium matrix ((3n-c)×b), B is the coordinate matrix (b×(3n-c)), and B=TT. Combining Eq. 2, Eq. 3 and Eq. 4 gives:
 |
(5) |
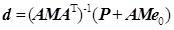 |
(6) |
Eq. 5 reflects the relationship among the initial defect length e0, load P and axial force t. Eq. 6 reflects the relationship among the initial defect length e0, load P and node displacement d. In the above equations, I is the unit matrix, tP is the additional axial force caused by load P, and te is the additional axial force caused by the initial defect length e0. Thus, when load P is a constant, the pre-stress deviations and shape deviations of the structure are caused by the original element length variation; when the member length changes by δe0, the pre-stress and shape change are:
 |
(7) |
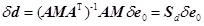 |
(8) |
where
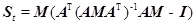 , for which St is the stress sensitivity matrix (b×b) and the parameter (St)ij reflects the magnification between the jth element’s original length change and the ith element’s pre-stress deviation, and Sd = (AMAT)-1AM, for which Sd is the shape sensitivity matrix ((3n-c)×b) and the parameter (Sd)ij reflects the magnification between the jth element’s original length change and the ith node’s displacement deviation. Therefore, Eq. 6 shows the relationship between the element length deviation and the pre-stress deviation.
, for which St is the stress sensitivity matrix (b×b) and the parameter (St)ij reflects the magnification between the jth element’s original length change and the ith element’s pre-stress deviation, and Sd = (AMAT)-1AM, for which Sd is the shape sensitivity matrix ((3n-c)×b) and the parameter (Sd)ij reflects the magnification between the jth element’s original length change and the ith node’s displacement deviation. Therefore, Eq. 6 shows the relationship between the element length deviation and the pre-stress deviation.
2.3. Error Effect Analysis of Different Construction Schemes
In a real cable-strut tensile structure, the structural members can be classified into two different types. The first type is the “active members” that help to lift the tensile structure. Their lengths are adjusted during the construction procedure. Their internal forces are recorded immediately by the jack and are controlled exactly. The second type is the ordinary “passive cables” that have a predetermined fixed slack length between two predefined joints. Their internal forces are produced passively according to the balance equation and geometric equation. Then, the pre-stress deviation is classified into active cable pre-stress deviation δtc and passive cable pre-stress deviation δtu. Similarly, the element length error can also be classified into active cable length error δec0 and passive cable length error δeu0. The stress sensitivity matrix St can be rewritten as:
 |
(9) |
During the construction procedure, the pre-stresses of the active cables were controlled exactly with the help of the jack, and the pre-stress deviation was zero. According to Eq. 9, the length adjustment values of the active cable are written as:
 |
(10) |
Then, the length adjustment values of all cables are written as:
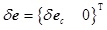 |
(11) |
Thus, the pre-stress deviations of all the passive cables can be obtained:
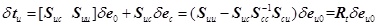 |
(12) |
When the active cable number is s,
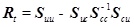 is the stress sensitivity matrix of the passive cables based on the condition that the pre-stress deviation of all the active cables are zero. The parameter (Rt)ij reflects the magnification between the jth element’s original length change and the ith passive cable’s pre-stress deviation. Comparing Eq. 7 and Eq. 12, the exact control for the active cable’s internal force will change the passive cable’s pre-stress deviation. In different construction schemes, different active cables will be adopted, and different error effects for the passive cables will be produced. After comparing the pre-stress deviation of different construction schemes, the optimal construction scheme can be selected for actual construction with minimum pre-stress deviation for all the passive cables.
is the stress sensitivity matrix of the passive cables based on the condition that the pre-stress deviation of all the active cables are zero. The parameter (Rt)ij reflects the magnification between the jth element’s original length change and the ith passive cable’s pre-stress deviation. Comparing Eq. 7 and Eq. 12, the exact control for the active cable’s internal force will change the passive cable’s pre-stress deviation. In different construction schemes, different active cables will be adopted, and different error effects for the passive cables will be produced. After comparing the pre-stress deviation of different construction schemes, the optimal construction scheme can be selected for actual construction with minimum pre-stress deviation for all the passive cables.
2.4. The Statistical Features of the Pre-stress Deviation
As discussed above, this study assumes that the errors are independent of each error and that the probability of positive or negative error is the same. Furthermore, the total error obeys the normal distribution N~(µei, σei), where µei and σei are the average value and the standard deviation for the ith element’s length error, respectively. According to Eq. 7 and probability statistics theory, when all the members are assembled with the designed length, the distribution of the initial pre-stress deviation of each element obeys the normal distribution N~(µti, σti), where µti and σti are the average value and standard deviation of the ith element’s internal force, respectively:
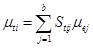 |
(13) |
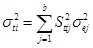 |
(14) |
According to Eq. 13 and Eq. 14, the pre-stress deviation effects caused by the element length error can be achieved and be used to evaluate the length error sensitivity of each type of element.
Similarly, the distribution of the initial pre-stress deviation of the passive cables also obeys the normal distribution N~(µti, σti) when the pre-stress in the active cables is controlled exactly, where µti and σti are the average value and the standard deviation of the ith passive cable’s internal force, respectively:
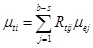 |
(15) |
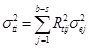 |
(16) |
According to Eq. 15 and Eq. 16, the pre-stress deviation effects in the passive cables caused by the element length error can also be achieved and be used to evaluate the error effects of different construction schemes. After comparing the pre-stress deviation effects of different construction schemes, the optimal construction scheme can be achieved with lower pre-stress deviation and a more convenient construction process.
3. EXAMPLE ANALYSIS
To test the proposed construction scheme optimization method, a cable-strut tensile structure with an outer diameter of 200 m and an inner diameter of 70 m is employed as a test (as shown in Fig. 1); its long strut is 20 m, and its short strut is 14 m. It is composed of 24 symmetrical cable-strut units and has 24 constraint nodes in the surrounding supports. The elasticity moduli of the cables and struts are Ec=1.7×108 kN/m2 and Es=2.1×108 kN/m2, respectively. The pre-stress distributions of each type of element in the symmetrical unit are listed in Table 3.
| Element number | Prestress t0 (kN) |
No active cables | Scheme 1 | Scheme 2 | Scheme 3 | ||||
|---|---|---|---|---|---|---|---|---|---|
| µti | σti | µti | σti | µti | σti | µti | σti | ||
| 1 | 2227.4 | 0 | 20.194 | 0 | 0.832 | 0 | 0 | 0 | 0 |
| 2 | 2058.4 | 0 | 18.661 | 0 | 0.808 | 0 | 0.124 | 0 | 0.118 |
| 3 | 2227.4 | 0 | 20.263 | 0 | 0 | 0 | 0.847 | 0 | 0 |
| 4 | 2058.4 | 0 | 18.728 | 0 | 0.125 | 0 | 0.824 | 0 | 0.118 |
| 5 | 7731.9 | 0 | 70.063 | 0 | 1.810 | 0 | 0.342 | 0 | 0.337 |
| 6 | 7731.9 | 0 | 70.314 | 0 | 0.342 | 0 | 1.822 | 0 | 0.337 |
| 7 | -403.7 | 0 | 3.677 | 0 | 0.296 | 0 | 0.299 | 0 | 0.284 |
| 8 | -538.3 | 0 | 4.888 | 0 | 0.122 | 0 | 0.116 | 0 | 0.065 |
According to Eq. 1 and Table 2, mathematical models of the element length error are established. According to Eq. 7, the sensitivity matrix St is established. Then, according to Eq. 13 and Eq. 14, when all the members are assembled with the designed length (for simplicity, this is denoted as the “no active cables” condition), the statistical characteristics of the pre-stress deviation were obtained and are listed in Table 3, which indicates the following: (1) Each element has a different element length error sensitivity. The error sensitivity of the hoop cables is the most prominent; the error sensitivity of the ridge cables and diagonal cables are lower, and that of the struts are the lowest. The lengths of those elements with high error sensitivity must be controlled exactly. (2) Because of the symmetry and considering no gravity effects, the ridge cables and diagonal cables have the same length error sensitivity. Similarly, strut 1, strut 2, the top hoop cables and the lower hoop cables have the same length error sensitivity.
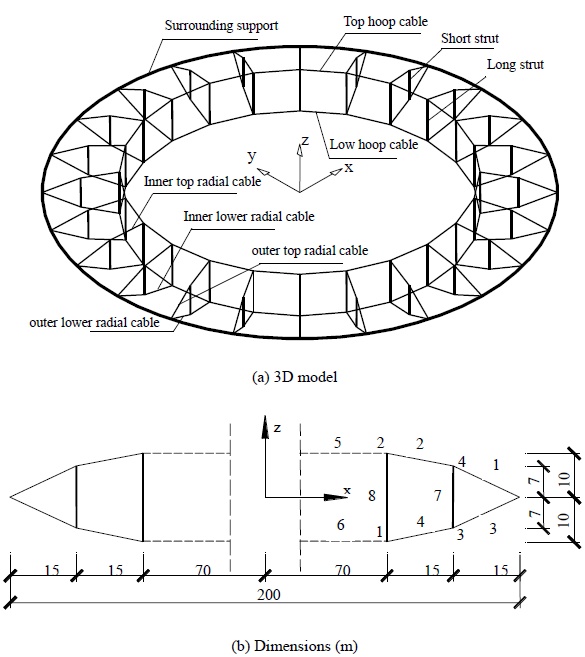
In this paper, three different construction schemes were analysed. The first scheme is to tension the outer lower radial cable. For simplicity, this is denoted as scheme 1. Scheme 2 is to tension the outer top radial cable. Scheme 3 is to tension both the outer top radial cables and lower radial cables. According to Eq. 12, the sensitivity matrix Rt is established. According to Eq. 15 and Eq. 16, the statistical characteristics of the passive cable pre-stress deviation, based on the pre-stress in the active cables are exactly controlled, can also be obtained for the above three construction schemes, as shown in Table 3, which indicates the following: (1) Because the element length errors are assumed to be independent of each other and because the probability of positive or negative errors are assumed to be the same, the statistical features µti of the pre-stress deviation are all zero. (2) By exactly controlling the pre-stress in the active cables, the statistical features σti under different construction scheme clearly decreased, meaning that the pre-stress deviation level decreased and the construction precision clearly increased compared to the “no active cables” construction condition when all the members were assembled with the designed length. (3) Because of the symmetry and no gravity effects, scheme 1 and scheme 2 have similar construction precision. For asymmetrical structures, tensioning the lower radial cable and top radial cable will have different construction error effects. (4) Compared to scheme 1 and scheme 2, scheme 3 has lower values of σti, indicating that it has higher construction precision. However, this scheme requires tensioning all the outer cables, and the total number of active cables is 48. Therefore, its construction procedure is more complicated, and its construction cost is higher; meanwhile, the increase in construction precision is not very significant. Thus, the optimal construction scheme should consider not only the construction precision but also the construction cost. After evaluating and comparing the error effects for different construction schemes, the optimal construction scheme can be selected for actual construction with the low error effects, low cost and more convenient construction.
CONCLUSION
This study investigated the optimization method of the construction scheme of cable-strut tensile structures. First, a mathematical model of the element length error was investigated based on stochastic theory. By combining the balance equation, geometric equation and physical equation, the fundamental relationship between the pre-stress deviation and the element length error was derived. Next, assuming that the pre-stress in the active cable to be zero, the relationship between the pre-stress deviation of a passive cable and the element length error was obtained. Then, statistical characteristics of the pre-stress deviation were obtained under different construction schemes using statistical theory. The following findings were obtained: (1) Different elements have different error sensitivities. (2) By exactly controlling the pre-stress in the active cables, the construction precision can be increased compared to the “no active cables” construction condition when all the members were assembled with the designed length. (3) Different construction schemes have different error effects. After analysing and comparing the error effects of different construction schemes, the optimal construction scheme, with lower error effects and lower construction costs, can be chosen for actual construction.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
The work was supported by the National Natural Science Foundation of China (Grant Nos. 51578422, 51678082 and 51308080), the Natural Science Foundation of Zhejiang Province (Grant No. LY14E080019), the Science and Technology Project of Zhejiang Province (Grant No. 2014C33013), the Science and Technology Project of the Ministry of Housing and Urban-Rural Development of China (Grant No. 2014-K3-005), and the Qinglan project of Jiangsu Province.


