All published articles of this journal are available on ScienceDirect.
Analysis of the Correlation Between Strength and Fractal Dimension of Gravelly Soil in Debris-flow Source Areas
Abstract
Particle size distribution of gravelly soil plays a crucial role in debris flow initiation. For better understanding the mechanism of debris flow formation, two crucial mechanical property parameters of the gravelly soil are required to be studied meticulously: hydraulic conductivity and strength. With the aim of measuring the composition of the gravelly soil, 182 soil samples were taken from debris flow prone areas. With the aid of a sieve test, the particle size distribution of the samples can be obtained and analyzed. Then fractal theory was employed to compute the fractal dimension of the soil samples. By analyzing the results of sieve test (particle size distribution curves) and the results of the fractal theory calculations, the relationship between fractal dimension and particle size distribution can be explored. The results illustrate that the particle compositions of the gravelly soil tends to remain uniform as the fractal dimension increases. Moreover, as the coarse particle content increases, the fractal dimension decreases. To better understand the formation mechanism of debris flows, direct shear tests were conducted. Subsequently the experimental results were analyzed. By analysis, the following conclusions can be drawn: the soil strength decreases as the fractal dimension increases, and for soils with lower moisture content and identical dry density, a linear relationship between fractal dimension and cohesion force was identified. Moreover, cohesion force and internal friction force both decrease as the fractal dimension increases, but the internal friction angle decreases slightly while the cohesion force decreases greatly. Therefore we concluded that soil strength decreased mainly due to the reduction in cohesion force.
1. INTRODUCTION
Debris flows occurred when masses of poorly sorted sediments are agitated and saturated with water and surge down the slope in response to gravity [1-3]. The amount of energy involved in such phenomena is enormous and their mobility is such that it allows them to propagate for several hundreds of metres without losing their destructive potential. Due to these characteristics, debris flows are considered to be among the most dangerous and catastrophic natural events [1, 4, 5]. Presently, accurate prediction based on critical rainfall is widely employed all over the world [6-8]. However, owing to the complexity of the debris-flow initiation mechanism, the prediction accuracy cannot satisfy the requirements of debris-flow prevention and mitigation. Prediction based on the debris-flow formation mechanism is the most effective approach for reducing debris-flow disasters. Previous researches have revealed that the strength and hydraulic conductivity of gravelly soil in the debris-flow source area play a crucial role during the process of debris-flow initiation [9-11], and both parameters are determined by particle composition. But the particle size distribution of the gravelly soil in the debris-flow source area is so wide that the particle grading feature is not yet well understood.
The composition and gradation of the particles in debris flow source areas have significant influence on debris flow formation, subsequent movement and resulting dynamic forces [12, 13]. Previous studies explored the characteristics of the gravelly soil [14, 15], and some models were established to reveal the relationship between mechanical properties of the gravelly soil and its particle size distribution [16-22], but due to the complexity of the composition of the particles, the existing models could not satisfy the requirements for accurate debris flow prediction and mitigation. In addition, the complexity of grain composition results in a non-deterministic and anisotropic gravelly soil structure, which poses great difficulties when attempting to use traditional methods based on linear analysis to quantitatively describe it. The fractal theory was developed to describe the qualities of complex shapes in nature. Fractal theory was first introduced by Mandelbrot in 1967. It is a simple and general method for describing complex problems and phenomena [23]. Fractals are spatial objects whose geometric characteristics include scale dependence, irregularity, and self-similarity [24]. Since the 1990s, this theory has been increasingly employed to study the deposition of debris flows and the value of the theory is recognized and appreciated by scholars both at home and abroad [25-30]. Previous studies concentrated mainly on features of debris-flow depositions. However, researches on the fractal features of gravelly soil in debris-flow source areas are still undeveloped, and the relationship between physical and mechanical properties and the fractal dimension is rarely considered in the literature. Therefore, fractal theory is employed in this paper with the objective of calculating the fractal dimension and analyzing the fractal features of gravelly soil. On the basis of the fractal features and fractal dimension, the direct shear tests are performed to reveal the relationship between strength and fractal dimension.
On the basis of the aforementioned analysis, to better understand the characteristics of the gravelly soil and reveal the relationship between mechanical property and particle compositions, fractal theory is employed in this paper to calculate the fractal dimension of the gravelly soil, and the fractal dimension is used as an index to describe the characteristics of grain compositions. Based on the results of fractal theory calculations, a direct shear test was performed to measure the relationship between soil strength and fractal dimension. The objective of this paper is to obtain the fractal features of the gravelly soil in the debris-flow source area and to establish a model that relates strength to fractal dimension. Such a model could facilitate the prediction and mitigation of debris flows.
2. MATERIALS AND METHOD
In this research, 182 soil samples were taken from 116 gullies that were identified as prone to debris flows. The soil samples were sorted and dried in the laboratory to facilitate the sieve tests. Using sieve tests, the characteristics of the particle compositions were acquired, the particle size distribution database can be established, and the particle size distribution curves were plotted in both plane-coordinate and double logarithmic coordinates.
2.1. Fractal Theory
The gravelly soil in the debris-flow source areas shared some similarities with the fragmented rocks. Therefore, the particle fractal dimension can be calculated through the rock-crushing model, which belongs to fractal theory. It is presumed that the diameter of the gravelly soil particle is R, while N(R) denotes the number of particles whose diameter is larger than R, and these two parameters satisfy the general fractal equation:
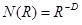 |
(1) |
Where D is the fractal dimension. After derivation we obtained Eq. 2:
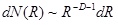 |
(2) |
The particle size and frequency of gravelly soil fits the Weibull distribution well:
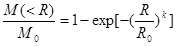 |
(3) |
Where M(<R) denotes the total mass of the particles whose diameter smaller than R, M0 is the total mass of the gravelly soil, RO is the average diameter of the gravelly soil, and k is a constant. For  , Eq. 3 was further manipulated, ignoring the quadratic term, and the following equation is obtained:
, Eq. 3 was further manipulated, ignoring the quadratic term, and the following equation is obtained:
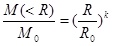 |
(4) |
From which we obtain equation 5:
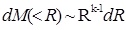 |
(5) |
The particle number of the gravelly soil and the mass of the gravelly soil satisfies the following equation:
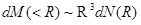 |
(6) |
Combining Eqs. (2), (5), and (6), the following equation can be derived:
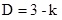 |
(7) |
Eq. 7 is the function employed in this paper to calculate the fractal dimension, where D is the fractal dimension, while k is the slope of the line we are fitting in the double logarithmic coordinates, where the X-axis is lg R and the Y-axis is lg[M(<R)/M0].
A fractal phenomenon approximates self-similarity or statistical self-similarity. This similarity exists only within a certain range of scales. Therefore the similarity will not exist outside certain ranges. Outside of this ranges the objects don’t have fractal features, which means the fractal scale-free interval is limited. On the basis of the complexity and particular nature of the gravelly soil, this paper chooses the coefficient of determination (R2) of the fitted line as the index to determine if the soil samples possess fractal features or not. If the coefficient of determination (R2) of the fitted line is greater than 0.9, it means that the soil samples present good similarity and the fractal dimension can be calculated through D=3-k. On the other hand, if the coefficient of determination (R2) of the fitted line is less than 0.9, the soil samples don’t have fractal features, and Eq. 7 cannot be employed to calculate the fractal dimension.
2.2. Fractal Features of the Gravelly Soil in Debris Flow Source Area
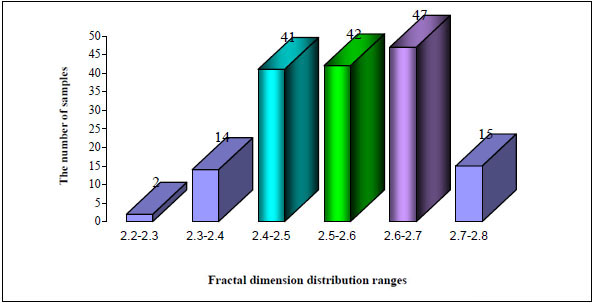
In total, 182 samples were taken from areas prone to debris flow (Fig. 1). The soil samples were prepared first (Fig. 2). Using sieve tests, the fundamental particle composition data were acquired and the particle size distribution curves were plotted using plane-coordinate and double logarithmic coordinates (Figs. 3 and 4). By means of linear fitting we obtained the slope of the straight line, and then Eq.7 was applied to calculate the fractal dimensions of all 182 soil samples. On analyzing the results, we found that the soil samples were mainly concentrated in one fractal dimension. About 161 soil samples satisfied the requirements of fractal theory well, and one fractal dimension accounted for 88.46% of the total samples. Therefore, we concluded that the gravelly soil is mainly concentrated in one fractal dimension. The dimension value ranges from about 2.25 to 2.98. The sample with the largest dimension was taken from Jiangjia gully, while the smallest was taken from Ganxi gully, and their double logarithm curves are depict in Fig. (4a and b), respectively. The distribution interval of one fractal dimension is illustrated in Fig. (5). Through Fig. (5), we found that the fractal dimensions of the 130 soil samples are within the range of 2.4-2.7, and one fractal dimension accounting for 80.75% of the total samples. This raises an obvious question: is it the case that gravelly soil with fractal dimension ranges from 2.4 to 2.7 is more susceptible to debris flow? This question merits further study in the future.
By comparing Figs. (3 and 4), we found that the particle composition tends to remain uniform as the fractal dimension increases. In addition, as the coarse particle content increases, the fractal dimension decreases. The particle compositions determined the skeleton of the gravelly soil, which in turn determines the strength and hydraulic conductivity.
Figs. (3 and 4) illustrates that the fractal dimension varied along with the particle size distribution. The more uniform the particle size distribution, the larger the fractal dimension becomes. The larger particles formed the skeleton of the gravelly soil, while the relatively smaller particles filled the pores. For soil samples with larger fractal dimension, the pores formed by larger particles are well filled with small particles. Under such circumstances, the hydraulic conductivity can be greatly reduced.


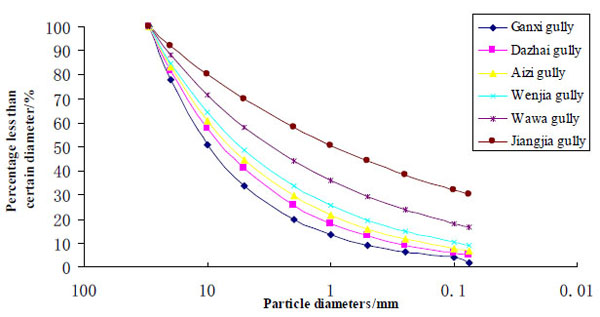
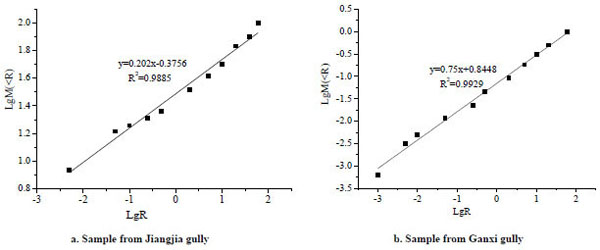
Moreover, the strength of the gravelly soil with larger fractal dimension is mainly provides by cohesion and sliding friction between particles. As the fractal dimension decreases, the porosity formed by larger particles could not be fully filled by the smaller particles. Therefore, the hydraulic conductivity becomes larger. For soil samples with smaller fractal dimension, the strength of the soil is mainly determined by cohesion and occlusal friction.
In addition, soil strength plays a crucial role in slope stability analysis. Debris-flow initiation can generally be subdivided into two mechanisms: 1) failure of shallow landslides, which transform into debris flows, and 2) concentrated run-off (flash flood) erosion in channels filled with sediments, which may be supplied by landslides from the slope [3, 31-34]. To better understand the debris-flow initiation mechanism, the relationship between strength, hydraulic conductivity, and particle composition required verification. With the aim of revealing the relationship between strength and fractal dimension, direct shear tests were conducted in the laboratory.
3. DIRECT SHEAR TEST
On the basis of the results described in section 2.2, a set of direct shear tests were designed. Through field investigation, we found that the antecedent moisture content of gravelly soil varied greatly. Thus the direct shear tests are divided into two groups, and the corresponding experimental program is shown in Table 1.
| Fractal dimension | Moisture content | Dry density(g/cm3) |
|---|---|---|
| 2.3 | Moisture content (13,15,17,19,21,23 and 25%) | 1.6 |
| 2.4 | 1.7 | |
| 2.5 | 1.8 | |
| 2.6 | 1.9 | |
| 2.7 | 2.0 | |
| 2.8 | ||
| Fractal dimension | Dry density (g/cm3) | Moisture content |
| 2.3 | Constant dry density(1.8) | 13% |
| 2.4 | 15% | |
| 2.5 | 17% | |
| 2.6 | 19% | |
| 2.7 | 21% | |
| 2.8 | 23% | |
| 25% |
Using the approach already described, we found that the fractal dimension ranges from about 2.25 to 2.798. Based on these fractal dimension values, we adopted 2.3, 2.4, 2.5, 2.6, 2.7, and 2.8 as our experimental values. By inverse calculation, the particle compositions under different fractal dimensions and different dry densities can be precisely computed. Due to the limitations of the experimental equipment and in order to avoid a scale effect, the maximum diameter of the particle is 2mm. An equivalent alternative method is employed to prepare the soil samples, and the detailed data are shown in Tables 2 and 3, respectively.
| Fractal dimension | Sample 1 | Particle percentage for different diameters | ||||
|---|---|---|---|---|---|---|
| 2.3 | Diameters (mm) | 1-2 | 0.5-1 | 0.25-0.5 | 0.075-0.25 | < 0.075 |
| Percentage | 38.44% | 23.66% | 14.57% | 13.28% | 10.04% | |
| 2.4 | Sample 2 | Particle percentage for different diameters | ||||
| Diameter (mm) | 1-2 | 0.5-1 | 0.25-0.5 | 0.075-0.25 | < 0.075 | |
| Percentage | 34.02% | 22.45% | 14.81% | 14.77% | 13.95% | |
| 2.5 | Sample 3 | Particle percentage for different diameters | ||||
| Diameter (mm) | 1-2 | 0.5-1 | 0.25-0.5 | 0.075-0.25 | < 0.075 | |
| Percentage | 29.29% | 20.71% | 14.64% | 15.99% | 19.36% | |
| 2.6 | Sample 4 | Particle percentage for different diameters | ||||
| Diameter (mm) | 1-2 | 0.5-1 | 0.25-0.5 | 0.075-0.25 | < 0.075 | |
| Percentage | 24.21% | 18.35% | 13.91% | 16.64% | 26.89% | |
| 2.7 | Sample 5 | Particle percentage for different diameters | ||||
| Diameter (mm) | 1-2 | 0.5-1 | 0.25-0.5 | 0.075-0.25 | < 0.075 | |
| Percentage | 18.77% | 15.25% | 12.39% | 16.25% | 37.34% | |
| 2.8 | Sample 6 | Particle percentage for different diameters | ||||
| Diameter (mm) | 1-2 | 0.5-1 | 0.25-0.5 | 0.075-0.25 | < 0.075 | |
| percentage | 12.94% | 11.27% | 9.81% | 14.12% | 51.86% | |
3.1. Test Processes and Phenomenon
The particle compositions under different fractal dimensions and different dry densities are calculated, respectively. Then with the aid of a balance with an indexing scale of one gram, all the required particles were weighed, then mixed with water(according to the desired moisture content) and stirred evenly to ensure that the samples were homogenous. Tape is used to seal the sample for 24 hours before carrying out the experiments. The samples were then installed in the test equipment, and the vertical pressures are set as 50, 100, 150, and 200kPa, respectively. The data collection system is then turned on to initiate the test process.
| Dry density (g/cm3) | Volume of the soil samples (cm3) |
Sample 1 | Fractal dimension | 2.3 | |||
|---|---|---|---|---|---|---|---|
| Diameter (mm) | 1-2 | 0.5-1 | 0.25-0.5 | 0.075-0.25 | < 0.075 | ||
| Mass (g) | 38.44% | 23.6% | 14.57% | 13.28% | 10.04% | ||
| 1.60 | 60 | 96 | 36.9 | 22.7 | 14.0 | 12.8 | 9.6 |
| 1.70 | 60 | 102 | 39.2 | 24.1 | 14.9 | 13.5 | 10.2 |
| 1.80 | 60 | 108 | 41.5 | 25.6 | 15.7 | 14.3 | 10.8 |
| 1.90 | 60 | 114 | 43.8 | 27.0 | 16.6 | 15.1 | 11.4 |
| 2.00 | 60 | 120 | 46.1 | 28.4 | 17.5 | 15.9 | 12.1 |
4. RESULTS AND INTERPRETATIONS
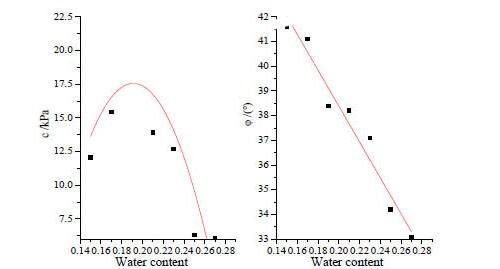
The whole experimental process is recorded. By analyzing the curves generated from the recorded data, we found that the soil strength decreases as the fractal dimension increases (soils under lower moisture content and identical dry density), and a linear relationship between fractal dimension and cohesion force was identified. In addition, the cohesion force and internal friction force both decreased(soil samples under different dry density and water content presenting similar characteristics, here we taking soil samples with dry density 1.8g/cm3 and water content 13% as an example to illustrate the relationship among cohesion force, internal friction angle and fractal dimension) as the fractal dimension increased (Figs. 6 and 7), but the internal friction angle decreased only slightly while the cohesion force decreased rapidly, from which we concluded that the soil strength decreased mainly due to the reduction in cohesion force.
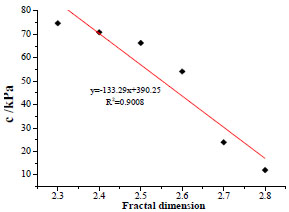
ρd = 1.8g / cm3 ,w = 13 %, whereρd is dry density and w is moisture content
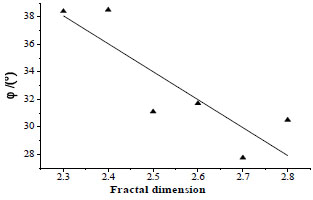
ρd = 1.8g / cm3 ,w = 13 %, whereρd is dry density and w is moisture content
For the same soil, the cohesion force initially increased and subsequently decreased with increasing moisture content, while the internal friction angle decreased continually with increasing moisture content. When the moisture content approached 20%, the cohesion force reaches its peak value (Fig. 8), and the results presented here agreed well with previous research findings [10].
5. DISCUSSIONS
The results of this paper revealed that particle size distribution plays an important role in the mechanical properties of the gravelly soil, which, in turn, greatly influences the initiation processes, dynamic feature, and impact forces of the debris flows. Through calculation and analysis, the following conclusions can be drawn: The fractal dimension is closely related to the particle size distribution, and the particle size distribution becomes evenly as the fractal dimension becomes larger. As fractal dimension decreases, the coarse particles dominate the soil skeleton, which determines the strength features of the gravelly soil.
By analyzing the direct shear test results, we found that the soil strength and fractal dimension show an inverse correlation. Fig. (6) reveals that the cohesion force and fractal dimension show a significant inverse correlation, which is mainly due to the variation in soil structure. For soil samples with small fractal dimensions, the coarse particles play a dominant role in the particle compositions. Under such circumstances, the occlusal forces between coarse particles are the main contribution to the soil strength. When the particle composition tends to be homogeneously, occlusal forces and internal friction forces both determine the soil strength. Moisture content plays a complex role in the variation of soil strength. By analyzing direct shear test phenomena, we found that as the moisture content increases, the soil strength first increases and subsequently decreases. The optimal moisture content is around 20%, which means that the soil strength reaches its peak value with moisture content 20%. Before the moisture content reaches 20%, the soil is a little drier, and when the moisture content increases, the water acts like paste, gluing the loose particles together and increasing the interaction forces (cohesion force). Soils with moisture content of around 20% are almost fully saturated. Under such conditions, if more water is added to the soil samples, the water will play two roles simultaneously. First, it acts as a lubricant, which greatly decreases the cohesion forces and the internal friction forces, and at the same time it provides a buoyancy force between particles, which is referred to as pore water pressure. As the total stress remains constant, the increasing of pore water pressure directly lead to decreasing effective stress.
CONCLUSION
The structure of gravelly soil in debris-flow source areas plays a key role in debris-flow initiation processes. Simultaneously, soil structure greatly influences its strength and hydraulic conductivity. The main objective of this paper is to reveal the relationship between soil strength and soil structure. To better understand the corresponding mechanism, fractal theory is employed to calculate the fractal dimensions of gravelly soil. Through calculation, the fractal features of the various gravelly soils can be analyzed and the ranges of the fractal dimensions can be determined. Finally, a fractal dimension database can be established and used in the subsequent design of the direct shear tests.
On the basis of fractal theory calculations, the following conclusions can be drawn: gravelly soil in debris-flow source areas are mainly concentrated in one fractal dimension, ranging from about 2.25 to 2.798. Moreover, the fractal dimension is closely related with the characteristics of the particle compositions, which tends to remain uniform as the fractal dimension increases.
As the coarse particle content increases, the fractal dimension decreases. Previous researches revealed that the fractal dimension significantly affected the hydraulic conductivity, and the corresponding model has been established. Debris-flow initiation is mainly influenced by two parameters: hydraulic conductivity and soil strength. With the aim of exploring the relationship between soil strength and fractal dimension, the results of direct shear tests were closely studied here. Following detailed analysis, the following conclusions can be drawn: Soil strength decreases as the fractal dimension increases. For soils with lower moisture content and identical dry density, a linear relationship between fractal dimension and cohesion force was identified. In addition, the cohesion force and internal friction force both decreased as the fractal dimension increased. However the internal friction angle decreased only slightly as the cohesion force decreased rapidly. Thus we concluded that the soil strength decreased mainly due to the reduction of the cohesion force.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
This work is financially supported by the doctoral fund of Henan Polytechnic University (Grant No B2015-58), the key deployment project of Chinese Academy of Sciences (KZZD-EW-05-01), the National Natural Science Foundation of China (51178402 & 41302284), Department of Transportation Technology Projects (2011 318740240) and CRSRI Open Research Program (Program SN: CKWV2015205/KY).


