All published articles of this journal are available on ScienceDirect.
Seismic Vulnerability and Fragility of Existing Italian Industrial Steel Buildings
Abstract
Introduction:
The recent L’Aquila (2009) and Emilia-Romagna (2012) Italian earthquakes have highlighted the vulnerability of recently erected buildings, with particular reference to industrial ones. Although steel buildings have usually demonstrated a good behaviour under earthquakes, with limited damages and rare cases of collapse, they still represent a structural typology at risk due to the significant exposure connected to the importance of the resources they host.
Methods:
In the paper a parametric study on several industrial steel buildings, different for typology, geometrical dimensions, seismic zones and snow geographic areas, has been done through pushover analyses.
Results and Conclusion:
The results have allowed to plot vulnerability curves, which have been compared to seismic fragility curves derived from literature observational studies. The comparison among curves has allowed to estimate the effectiveness of the literature fragility studies, as well as to evaluate the seismic damages suffered by investigated structures under dissimilar grade earthquakes.
1. INTRODUCTION
The most of the Italian built heritage consists of buildings constructed without appropriate anti-seismic design rules, as they were erected in those regions that, before of the new technical legislative measures, were not considered as seismic zones. In fact, it is noted that strict regulations for constructions in seismic areas were always promulgated, beginning from the purely prescriptive standards at the start of the nineteenth century, to decrees issued after some destructive earthquakes, like those in Reggio Calabria (1905) and in Messina (1908). Nevertheless, only after the seismic event occurred in San Giuliano di Puglia (2002), that caused the disastrous collapse of the primary school Jovine, the application of these regulations to the entire national territory became mandatory. Before this year, only the areas where earthquakes struck were classified as seismic zones, while for the remaining areas compliances to build with anti-seismic regulations were not required.
The recent L’Aquila (2009) and Emilia-Romagna (2012) Italian earthquakes have highlighted the vulnerability of the Italian built heritage, with reference not only to the historical buildings, but also to the recently erected industrial constructions. In this direction, an example is the town of Mirandola (district of Modena), where 80% of industrial buildings, mostly made of pre-stressed reinforced concrete (r.c.), were destroyed or considered to be unfit for use after seismic events occurred on 2009 May 20th and 29th [1]. The constructive peculiarity of these buildings, that are much widespread all over the Italian country, is the easy erection process based on hinged beam-to-column joints. Contrary, this building typology is particularly sensible to horizontal actions (Fig. 1a), especially when additional structural systems, such as cranes and pallet racks, are placed inside them. In this paper the attention is dedicated to the industrial steel buildings that, despite they suffered limited damages (Fig. 1b) compared to those of pre-stressed r.c. structures, were designed without suitable seismic rules introduced in Italy since 2003 only.

Generally, the industrial steel frame buildings assure high levels of reliability in case of earthquake, considering that many of them, although they were not designed to resist seismic actions, remained either unharmed or suffered limited damage. Moreover, steel framed structures designed to withstand gravity and wind loads only, exhibit a very satisfactory behaviour under exceptional actions [2-4]. The only cases of collapse are mostly conditioned by the failure of pallet racks that, often reaching considerable heights, represent real structures inside the industrial building and, therefore, they need an appropriate seismic design (Fig. 1c and d). During last Italian earthquakes, in Abruzzo and Emilia-Romagna most of industrial shelving suffered collapses and significant damages (Fig. 1e), contributing in the worst cases to the collapse of the entire structure, in addition to the loss of numerous products, like foodstuffs, which were stored there. The issue is, therefore, very important in terms of social and economic safety. In fact, in the case of industrial buildings, the issue of the life safety is associated to the theme of the safeguard of the values exposed at risk and, above all, to the continuity of business activities after the earthquake. In the paper the seismic behaviour of some industrial steel buildings has been assessed through non-linear static analyses which allowed to plot, starting from pushover curves, their vulnerability curves used to know exhaustively the expected seismic damages suffered under earthquakes of different intensity with reference to different limit states. Considering the difficulty to investigate all varieties of existing industrial buildings, only some of the most common types detected in Italy, representative of the industrial steel buildings heritage, have been examined. In particular, identification and analysis of a number of typical buildings, different each other for geometric dimensions and constraint conditions, have been done, as it will be shown in the next sections.
2. MATERIAL AND METHODS
2.1. THE INDUSTRIAL ARCHITECTURE: FROM UNUSED AREAS TO THE CITY REBIRTH
Industrial buildings cannot be considered artifacts unrelated to the architecture. In fact, many of them for their intrinsic and formal characteristics, are examples of great architectural value. Works of this kind can be found throughout history (Fig. 2), as a clear demonstration of how a building typology, such as the industrial one, which could appear seemingly cut off from architecture, is instead an integral part of it.

It is not a coincidence that, when taking in consideration industrial architectures conceived as the result of a design based on a constant interaction between construction (technological, scientific, production) aspects and poetic contents, their shape depending on the function, location, climate and context of the building can be easily changed.
The aforementioned factors distinguish a work of architecture and differentiate the industrial work from the construction of a common building. Technique transforms into artistic expression and, therefore, in poetry. Renato De Fusco, an architecture historian, expresses this concept in semiological terms, such as “meaning” and “significant”, “living space” and “invasion “, “contents” and “contain” [8]. In other words, when the interior space (meaning) relies only to the covering and to the structure of the living space, leaving intact the content (significant), a technically pure event, that is an inevitable collusion between engineering and architecture, is testified.
When, instead, the internal structural conformation is clearly manifested also outside, giving a totally new interior - exterior relationship, it is not correct to mention technique and architecture separately, but architecture is able to embrace numerous techniques of building science and structural engineering. With these achievements, an industrial architecture is identified. Another important aspect is that the industrial complexes abandoned after the cessation of working activities leave voids in the urban pattern and they remain suspended between the absence of the present and the memory of the past. This shows a functionality lost but, at the same time, a future potential to become something else. Focusing attention on this structural typology, a possible reconversion could be useful as social, urban and architectural requalification process. Industrial buildings are connected to the productive heart of the city and helped to form the identity of the area. Therefore, even when they stop production activities, they must maintain the link of integration with the entire urban context.
3. SELECTION OF STRUCTURAL TYPOLOGIES
Generally, one-story buildings for industrial use are characterised by regular plan layouts having large spans with minimum encumbrance of structural elements. Usually, the longitudinal distance among columns ranges from 5 to 15 m, while the transversal one varies from 15 to 30 m. The inner height between the work plane (about 1 m far from the floor) and the lowest point of the roof intrados is often contained between 5 and 15 m.
Obviously, these dimensional values are only for guidance and they are usually variable depending on the types and structural elements employed. In order to be able to assess more accurately the variability fields of these buildings, a significant number of projects and real case studies, from which the most recurrent plan and in elevation average sizes for each type are derived, have been collected [9].
Subsequently, the selected types have been divided into classes depending on both the type and the slope of roof beams. Finally, for each of the case studies selected, lattice girders or I beams have been considered. The structural schemes adopted have been designed on the basis of the regulations at the time of their realization through a simulated design process. After defining the individual sub-models (geometrical, mechanical and loading) characterising the structural numerical model, the simulated design has been carried out considering the variability of various parameters associated to the constraint conditions, the dimensional aspects and the geographical area where structures are located.
The geometrical model has been defined considering the variability of the most common structural schemes symbolising the industrial steel buildings. After identifying the more representative model of each investigated structural type, having given average dimensions, different schemes of the same structural system, but with different sizes of columns (h) and roof beams (h') depths, as well as with changed restraint conditions (hinge (H) or encastre (E)), have been numerically examined. With reference to this latter issue, as base restraint types the partially restrained connections, which however exhibit in seismic zone a good behaviour [10, 11], have not been considered. Furthermore, the upper beams of the examined structural schemes have been constrained to the columns with either rigid or shear connections, the latter showing also a reasonable ductile capacity under earthquakes [12]. All schemes subjected to the seismic vulnerability assessment are shown in Fig. (3).
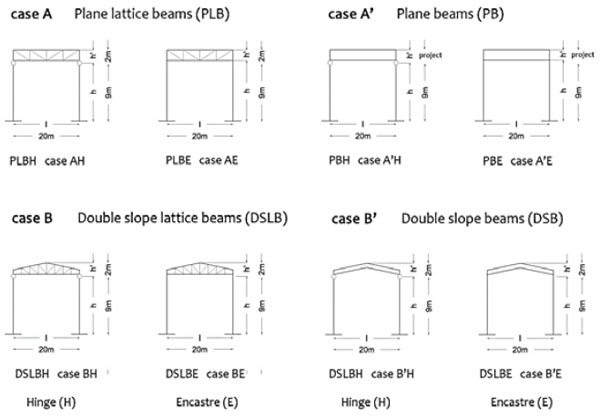
The investigated frames are identified with acronyms according to both the type of structural elements used for roofing systems (plane lattice beams (PLB), plane beams (PB), double slope lattice beams (DSLB) and double slope beams (DSB)) and the constraint conditions (hinge (H) or encastre (E)).
Then, such schemes have been identified by the letters A, A’, B and B' and, for each of them, two different constraint conditions have been contemplated, leading to the definition of the following eight structural systems: AH, AE, A’H, A’E, BH, BE, B’H and B’E. For the first two structural patterns (AH and AE), a variability of the dimensions h and h' for the execution of a more wide parametric analysis has also been hypothesized. In such a case, starting from a reference case study with assigned average dimensions (l =20m, h=9m and h'= 2m), the field of investigation has been expanded by considering possible variations of the geometric parameters h and h', which gave rise to thirty cases of analysis considering as base restraints hinges (Table 1) or full rigid (Table 2) joints.
The mechanical model of the structures has been implemented by defining the nature of the materials used. In the case under question it has been used a S275 steel type with characteristics intermediate between the mild steels commonly used in the constructive practice. Finally, with regard to the loads acting on the structures and, therefore, to the loading model, gravitational actions linked to the masses of structural and non-structural elements have been considered and the characteristic values of the variable actions due to snow, wind and earthquake have been computed. The AH and AE structural schemes analysed considering the variability of Italian climatic zones are depicted in Table 3.
| Label | l | h | h’ | |
|---|---|---|---|---|
| Frames AH1 | AH11(l=20, h=6,h’=1.5) | 20m | 6m | 1.5m |
| AH12(l=20, h=6,h’=2) | 2m | |||
| AH13(l=20, h=6,h’=2.5) | 2.5m | |||
| AH14(l=20, h=6,h’=3) | 3m | |||
| AH15(l=20, h=6,h’=3.5) | 3.5m | |||
| Frames AH2 | AH21(l=20, h=9,h’=1.5) | 9m | 1.5m | |
| AH22(l=20, h=9,h’=2) | 2m | |||
| AH23(l=20, h=9,h’=2.5) | 2.5m | |||
| AH24(l=20, h=9,h’=3) | 3m | |||
| AH25(l=20, h=9,h’=3.5) | 3.5m | |||
| Frames AH3 | AH31(l=20, h=9,h’=1.5) | 12m | 1.5m | |
| AH32(l=20, h=9,h’=2) | 2m | |||
| AH33(l=20, h=9,h’=2.5) | 2.5m | |||
| AH34(l=20, h=9,h’=3) | 3m | |||
| AH35(l=20, h=9,h’=3.5) | 3.5m | |||
| Label | l | h | h’ | |
|---|---|---|---|---|
| Frames AE1 | AE11(l=20, h=6,h’=1.5) | 20m | 6m | 1.5m |
| AE12(l=20, h=6,h’=2) | 2m | |||
| AE13(l=20, h=6,h’=2.5) | 2.5m | |||
| AE14(l=20, h=6,h’=3) | 3m | |||
| AE15(l=20, h=6,h’=3.5) | 3.5m | |||
| Frames AE2 | AE21(l=20, h=9,h’=1.5) | 9m | 1.5m | |
| AE22(l=20, h=9,h’=2) | 2m | |||
| AE23(l=20, h=9,h’=2.5) | 2.5m | |||
| AE24(l=20, h=9,h’=3) | 3m | |||
| AE25(l=20, h=9,h’=3.5) | 3.5m | |||
| Frames AE3 | AE31(l=20, h=9,h’=1.5) | 12m | 1.5m | |
| AE32(l=20, h=9,h’=2) | 2m | |||
| AE33(l=20, h=9,h’=2.5) | 2.5m | |||
| AE34(l=20, h=9,h’=3) | 3m | |||
| AE35(l=20, h=9,h’=3.5) | 3.5m | |||
Actually, all the factors to be analysed for an extensive parametric analysis would be significantly numerous, but this paper refers to a particular selection of some typological, dimensional and geographical variables only. Geographic variability is linked to the location of the structural system and it influences the entity of seismic and variable (wind and snow) loads considered. With reference to these former loads, by taking into account the three climatic zones representative of the Northern, Central and Southern regions of the Italian country, indicated with I, II and III in Table 3, the number of analyses have been increased from 36 to108 (see Tables from 3 to 9).
After defining the geometry and global dimensions of the various structural systems to be investigated, considering all possible loads applied, the design of individual profiles to be employed have been done. The structures of the lattice girders have been obtained by coupling two profiles with channel or angle cross-sections: the former (UPN) has been assumed for the upper chords (U.C.) and the lower ones (L.C.), while the latter (L) has been chosen for the diagonal members (D.M.). For the structural type with plane beam (P.B.), HEB700/800/900 profiles, with a variability essentially conditioned by the geographical location of each structural scheme, have been used.
As a first step, the values of the more heavy stresses related to the different load combinations for each structural element have been collected, so to identify the most suitable profiles to be adopted for each individual component of the analysed systems. This design phase has been performed through a simulated design process according to the prevailing regulations at the construction time of these structures, essentially based on the Allowable Stress method contemplated in the old Italian code on steel structures [13] (Table 10).
The check of structures has been done by means of the actual Italian code [14], allowing to confirm or not the dimensions originally assigned to frame members (Table 11). This verification phase has been performed by using the finite element analysis program SAP 2000 [15].
From the comparison between the frames dimensioned according to the two different code approaches, a minimum difference of weight, with an average percentage difference equal to 1.26%, emerges. This means that the seismic actions do not affect the design of these structures, whose design is essentially dictated by the wind loads only. As a consequence, high levels of structural reliability of these structural types also according to the new seismic code are assured.
| Label | Label | l | h | h’ | Zone | ||||
|---|---|---|---|---|---|---|---|---|---|
| Frames AH1 | AH11z1(l=20, h=6,h’=1.5) |
Frames EH1 Frames AH1 |
AE11z1(l=20,h=6,h’=1.5) | 20m | 6m | 1.5m | I | ||
| AH11z2(l=20, h=6,h’=1.5) | Frames AE1 | AE11z2(l=20,h=6,h’=1.5) | II | ||||||
| AH11z3(l=20, h=6,h’=1.5) | AE11z3(l=20,h=6,h’=1.5) | III | |||||||
| AH12z1(l=20, h=6,h’=2) | AE12z1(l=20,h=6,h’=2) | 2m | I | ||||||
| AH12z2(l=20, h=6,h’=2) | AE12z2(l=20,h=6,h’=2) | II | |||||||
| AH12z3(l=20, h=6,h’=2) | AE12z3(l=20,h=6,h’=2) | III | |||||||
| AH13z1(l=20, h=6,h’=2.5) | AE13z1(l=20,h=6,h’=2.5) | 2.5m | I | ||||||
| AH13z2(l=20, h=6,h’=2.5) | AE13z2(l=20,h=6,h’=2.5) | II | |||||||
| AH13z3(l=20, h=6,h’=2.5) | AE13z3(l=20,h=6,h’=2.5) | III | |||||||
| AH14z1(l=20, h=6,h’=3) | AE14z1(l=20,h=6,h’=3) | 3 m | I | ||||||
| AH14z2(l=20, h=6,h’=3) | AE14z2(l=20,h=6,h’=3) | II | |||||||
| AH14z3(l=20, h=6,h’=3) | AE14z3(l=20,h=6,h’=3) | III | |||||||
| AH15z1(l=20, h=6,h’=3.5) | AE15z1(l=20,h=6,h’=3.5) | 3.5m | I | ||||||
| AH15z2(l=20, h=6,h’=3.5) | AE15z2(l=20,h=6,h’=3.5) | II | |||||||
| AH15z3(l=20, h=6,h’=3.5) | AE15z3(l=20,h=6,h’=3.5) | III | |||||||
| Label | Label | l | h | h’ | Zone | ||||
| Frames AH2 | AH21z1(l=20, h=9,h’=1.5) |
Frames EH1 Frames AH1 |
AE21z1(l=20,h=9,h’=1.5) | 20m | 9m | 1.5m | I | ||
| AH21z2(l=20, h=9,h’=1.5) | Frames AE2 | AE21z2(l=20,h=9,h’=1.5) | II | ||||||
| AH21z3(l=20, h=6,h’=1.5) | AE21z3(l=20,h=9,h’=1.5) | III | |||||||
| AH22z1(l=20, h=9,h’=2) | AE22z1(l=20,h=9,h’=2) | 2m | I | ||||||
| AH22z2(l=20, h=9,h’=2) | AE22z2(l=20,h=9,h’=2) | II | |||||||
| AH22z3(l=20, h=9,h’=2) | AE22z3(l=20,h=9,h’=2) | III | |||||||
| AH23z1(l=20, h=9,h’=2.5) | AE23z1(l=20,h=9,h’=2.5) | 2.5m | I | ||||||
| AH23z2(l=20, h=9,h’=2.5) | AE23z2(l=20,h=9,h’=2.5) | II | |||||||
| AH23z3(l=20, h=9,h’=2.5) | AE23z3(l=20,h=9,h’=2.5) | III | |||||||
| AH24z1(l=20, h=9,h’=3) | AE24z1(l=20,h=9,h’=3) | 3 m | I | ||||||
| AH24z2(l=20, h=9,h’=3) | AE24z2(l=20,h=9,h’=3) | II | |||||||
| AH24z3(l=20, h=9,h’=3) | AE24z3(l=20,h=9,h’=3) | III | |||||||
| AH25z1(l=20, h=9,h’=3.5) | AE25z1(l=20,h=9,h’=3.5) | 3.5m | I | ||||||
| AH25z2(l=20, h=9,h’=3.5) | AE25z2(l=20,h=9,h’=3.5) | II | |||||||
| AH25z3(l=20, h=9,h’=3.5) | AE25z3(l=20,h=9,h’=3.5) | III | |||||||
| Frames AH3 | AH31z1(l=20, h=12,h’=1.5) |
Frames EH1 Frames AH1 |
AE31z1(l=20,h=12,h’=1.5) | 20m | 12m | 1.5m | I | ||
| AH31z2(l=20, h=12,h’=1.5) | Frames AE3 | AE31z2(l=20,h=12,h’=1.5) | II | ||||||
| AH31z3(l=20, h=12,h’=1.5) | AE31z3(l=20,h=12,h’=1.5) | III | |||||||
| AH32z1(l=20, h=12,h’=2) | AE32z1(l=20,h=12,h’=2) | 2m | I | ||||||
| AH32z2(l=20, h=12,h’=2) | AE32z2(l=20,h=12,h’=2) | II | |||||||
| AH32z3(l=20, h=12,h’=2) | AE32z3(l=20,h=12,h’=2) | III | |||||||
| AH33z1(l=20, h=12,h’=2.5) | AE33z1(l=20,h=12,h’=2.5) | 2.5m | I | ||||||
| AH33z2(l=20, h=12,h’=2.5) | AE33z2(l=20,h=12,h’=2.5) | II | |||||||
| AH33z3(l=20, h=12,h’=2.5) | AE33z3(l=20,h=12,h’=2.5) | III | |||||||
| AH34z1(l=20, h=12,h’=3) | AE34z1(l=20,h=12,h’=3) | 3 m | I | ||||||
| AH34z2(l=20, h=12,h’=3) | AE34z2(l=20,h=12,h’=3) | II | |||||||
| AH34z3(l=20, h=12,h’=3) | AE34z3(l=20,h=12,h’=3) | III | |||||||
| AH35z1(l=20, h=12,h’=3.5) | EH35z1(l=20,h=12,h’=3.5) | 3.5m | I | ||||||
| AH35z2(l=20, h=12,h’=3.5) | EH35z2(l=20,h=12,h’=3.5) | II | |||||||
| AH35z3(l=20, h=12,h’=3.5) | EH35z3(l=20,h=12,h’=3.5) | III | |||||||
| Label | l | h | h’ | Zones | ||
|---|---|---|---|---|---|---|
| Frames A'H1 | A'H1z1(l=20, h=9,h’=?) | 20m | 9m | 0.9m 0.7m | I | |
| A'H1z2(l=20, h=9,h’=?) | II | |||||
| A'H1z3(l=20, h=9,h’=?) | III | |||||
| Label | l | h | h’ | Zones | ||
|---|---|---|---|---|---|---|
| Frames A'E1 | A'E1z1(l=20, h=9,h’=?) | 20m | 9m | 0.8m 0.7m | I | |
| A'E1z2(l=20, h=9,h’=?) | II | |||||
| A'E1z3(l=20, h=9,h’=?) | III | |||||
| Label | l | h | h’ | Zones | ||
|---|---|---|---|---|---|---|
| Frames BH1 | BH1z1(l=20, h=9,h’=2) | 20m | 9m | 2m | I | |
| BH1z2(l=20, h=9,h’=2) | II | |||||
| BH1z3(l=20, h=9,h’=2) | III | |||||
| Label | l | h | h’ | Zones | ||
|---|---|---|---|---|---|---|
| Frames BE1 | BE1z1(l=20, h=9,h’=2) | 20m | 9m | 2m | I | |
| BE1z2(l=20, h=9,h’=2) | II | |||||
| BE1z3(l=20, h=9,h’=2) | III | |||||
| Label | l | h | h’ | Zones | ||
|---|---|---|---|---|---|---|
| Frames B’H1 | B’H1z1(l=20, h=9,h’=2) | 20m | 9m | 2m | I | |
| B’H1z2(l=20, h=9,h’=2) | II | |||||
| B’H1z3(l=20, h=9,h’=2) | III | |||||
| Label | l | h | h’ | Zones | ||
|---|---|---|---|---|---|---|
| Frames B’E1 | B’E1z1(l=20, h=9,h’=2) | 20m | 9m | 2m | I | |
| B’E1z2(l=20, h=9,h’=2) | II | |||||
| B’E1z3(l=20, h=9,h’=2) | III | |||||
| Frames | L.C. | U.C. | D.M. | Columns | Weights [KN] | |
|---|---|---|---|---|---|---|
| AH1 | AH13z1 (l=20, h=6, h’=2.5) | UPN 140 | UPN 200 | 90x10 | HEB 220 | 80.1 |
| AH13z2 (l=20, h=6, h’=2.5) | UPN 140 | UPN 220 | 90x12 | HEB 260 | 85.3 | |
| AH13z3(l=20, h=6, h’=2.5) | UPN 100 | UPN 180 | 90x7 | HEB 280 | 78.5 | |
| AH2 | AH23z1 (l=20, h=9, h’=2.5) | UPN 140 | UPN 200 | 90x10 | HEB 280 | 91.4 |
| AH23z2 (l=20, h=9, h’=2.5) | UPN 140 | UPN 220 | 90x12 | HEB 300 | 98.4 | |
| AH23z3(l=20, h=9, h’=2.5) | UPN 100 | UPN 180 | 90x7 | HEB 360 | 93.3 | |
| AH3 | AH33z1(l=20, h=12, h’=2.5) | UPN 140 | UPN 200 | 90x10 | HEB 320 | 104.1 |
| AH33z2(l=20, h=12, h’=2.5) | UPN 140 | UPN 220 | 90x12 | HEB360 | 112.5 | |
| AH33z3(l=20, h=12, h’=2.5) | UPN 100 | UPN 180 | 90x7 | HEM320 | 130.9 | |
| Total | 874.5 | |||||
| Frames | L.C. | U.C. | D.M. | Columns | Weights [KN] | |
|---|---|---|---|---|---|---|
| AH1 | AH13z1 (l=20, h=6, h’=2.5) | UPN 140 | UPN 180 | 90x9 | HEB 220 | 77.6 |
| AH13z2 (l=20, h=6, h’=2.5) | UPN 160 | UPN 200 | 90x10 | HEB 260 | 84.7 | |
| AH13z3(l=20, h=6, h’=2.5) | UPN 100 | UPN 140 | 80x10 | HEB 280 | 78.1 | |
| AH2 | AH23z1 (l=20, h=9, h’=2.5) | UPN 140 | UPN 180 | 90x9 | HEB 280 | 89.9 |
| AH23z2 (l=20, h=9, h’=2.5) | UPN 160 | UPN 200 | 90x10 | HEB 300 | 95.7 | |
| AH23z3(l=20, h=9, h’=2.5) | UPN 100 | UPN 140 | 80x10 | HEB 400 | 96.1 | |
| AH3 | AH33z1(l=20, h=12, h’=2.5) | UPN 140 | UPN 180 | 90x9 | HEB 400 | 109.9 |
| AH33z2(l=20, h=12, h’=2.5) | UPN 160 | UPN 200 | 90x10 | HEM 280 | 122.9 | |
| AH33z3(l=20, h=12, h’=2.5) | UPN 100 | UPN 140 | 80x10 | HEM320 | 130.6 | |
| Total | 889.5 | |||||
4. NON-LINEAR ANALYSES AND CAPACITY CURVES
The seismic response of the structures under study has been evaluated by non-linear static analyses carried out through the calculation program SAP2000 [15]. A lumped plasticity modelling for structural elements has been adopted by defining the behaviour of the plastic hinges in terms of generalized force-displacement curves. The non-linear behaviour of beams has been taken of elastic-plastic type [16]. For columns, instead, it has been defined a resistance domain considering the simultaneous application of compressive and bending stresses. The analyses have been conducted under displacement control, assuming as control point the geometric centre of gravity of the roofing.
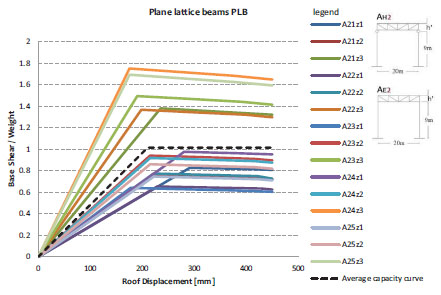
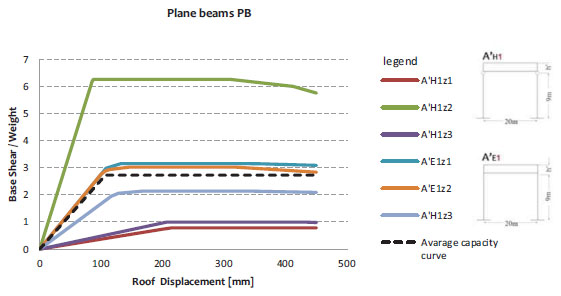
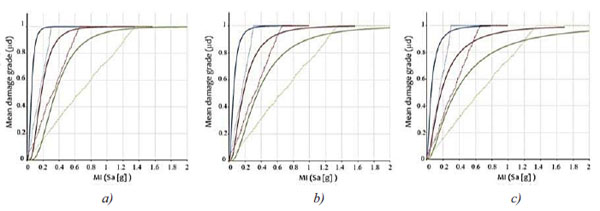
Given the considerable number of frames analysed, their subdivision into classes has been done and a capacity curve representative for each of them has been plotted. The cases presented have been divided according to the types and the constraint conditions, also considering further variables, such as the geometric dimensions and the geographical location. For the early two cases AH and AE, indicative of the type with plane lattice beams (PLB), a parametric analysis has been conducted considering the height of columns (6m, 9m, 12m) and the roofing systems one (1.5m, 2.0m, 2.5m, 3.0m, 3.5m) as variable parameters. Therefore, a further subdivision of each of the above-mentioned schemes in the three subcases (AH1, AH2, AH3 and AE1, AE2, AE3) has been made (see Tables 1 and 2). For all the other cases (A’, B and B’), where other additional variabilities, other than the different constraint conditions and the diverse geographical location, have not been considered, three representative capacity curves, one for each structural type, have been derived. Therefore, in accordance with the preceding subdivision, nine capacity curves representative of the different frames analysed, have been obtained and compared each to other, so to grasp typical behaviour and peculiarities of the different classes of structures examined.
The analysis results have been represented in terms of base shear, normalised to the total weight of the structural system, versus the displacement of a control point coincident with the gravity centre of the roofing. The representative capacity curve, characterised by a bilinear shape (typical of a SDOF system), corresponds to the average of the family of curves obtained for each class of frames (Fig. 4). This is determined on the basis of the average stiffnesses and strengths of the various structural schemes examined.
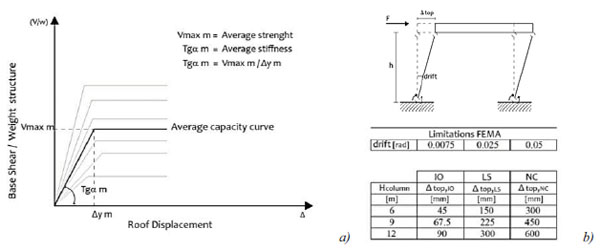
Another aspect to be considered for defining the capacity curves is the assessment of the ultimate displacement Δu related to the structure collapse mechanism. This value is taken on the basis of the FEMA 356 regulations [17], which are more complete and detailed than the Eurocode 8 provisions. This choice has been justified, besides, by the chance to compare the results with those proposed by other scientific researches dealing with similar topics [18]. The structure capacity in terms of displacement has been carried out on the basis of the FEMA legislative provisions, which refer to predefined maximum values of the inter-story drift: 0.0075 for immediate occupancy (IO), 0.025 for life safety (LS) and 0.05 for near collapse (NC). Therefore, considering the variability of the column height (6, 9 and 12m), the ultimate displacement assumes the values of 300, 450 and 600mm, respectively, as shown in Fig. (4). For the sake of example, Figs. (5 to 8) show the non-linear behaviour of structural schemes with height of 9m.
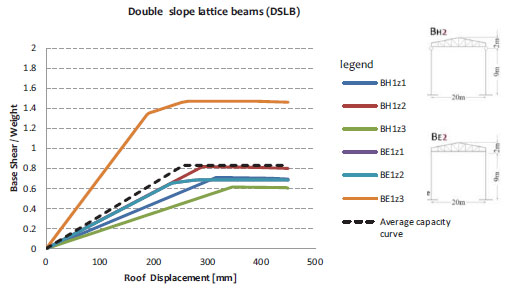
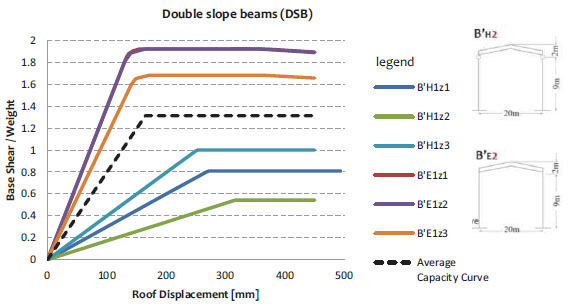
5. VULNERABILITY AND FRAGILITY CURVES
In case of earthquake, each structural system is exposed to a risk correlated to both human lives loss and the damage degree that it can exhibit. In the seismic risk analysis, in fact, it is necessary to translate the knowledge of the built vulnerability in the damage that can occur as a result of earthquakes having different magnitudes. The seismic risk parameter of a system R can be expressed as a function of its vulnerability V, of the parameter s, related to the severity of the earthquake, and of the parameter d, intended as measure of the damage, by means of a correlation law R = R (V, d, s).
One of the tools for the determination of the structure seismic risk and, therefore, of the above-mentioned functional link, is represented by the fragility curves. As already shown in some literature applications related to steel [19] and RC precast [20] industrial constructions, they provide the probability of a structural system exposed to a seismic input assigned to overcome certain levels of damage. In this paper two procedures have been used for deriving fragility curves of investigated structures. The first is a discretised procedure, punctually derived from the curves of capacity, which gives rise to those that will be defined as vulnerability curves, whereas the second procedure is an analytical method based on some literature indications. For the seismic reliability assessment of the structures, the current research trends are directed towards rigorous probabilistic approaches, involving both random and deterministic variables, that often are difficult to be considered at all in the project. For this reason, it has been herein proposed and developed a procedure simpler than that based on analytical formulations. The procedure presented allows to validate, through appropriate comparisons, the effectiveness of the fragility curves to estimate the seismic damages of structures subjected to earthquakes having different intensities.
The discrete / manual procedure evaluates the structural capacity and compares it directly with the demand related to an assigned seismic event on the basis of a limit state considered. In this work, based on the FEMA 356 guidelines, three performance levels (IO, LS, NC), characterised by appropriate values of inter - story drifts, have been taken into account. Starting from the structural behaviour in the non-linear static field, some damage levels of the structure, corresponding to the limits above defined by FEMA 356 provisions, have been taken into account and, for each earthquake with a given hazard level, the expected damages have been estimated by simply correlating the capacity displacement (or inter-story drift) with the demand one. The ratio between the demand parameter and the capacity one is then correlated to the damage levels of the EMS 98 scale [21] normalised in the range [0-1]. By varying the earthquake intensity and, therefore, the seismic demand, for each of the three limit states considered, the above ratio is calculated, allowing to plot step-by-step the structure fragility in a simple way, so leading to the so-called vulnerability curve. For the sake of example, in Fig. (9), the vulnerability curves of the scheme AE2 with h=9 m and full rigid base restraints are plotted.
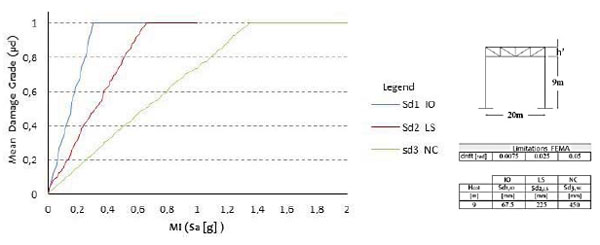
Later on, wanting to evaluate the propensity at damage of the examined industrial steel buildings considering the random nature of the earthquake, a peak ground acceleration of the demand spectrum variable between 0.01g and 1g has been considered. It is interesting to note that, as for this procedure, the first examples of vulnerability curves were referred to a conventional scheme that simplified the assessment procedure of the seismic vulnerability [22]. So, the general procedure involving a large number of points of the curve can be replaced by a simpler method, which is based, in absence of additional information, on two parameters only: the collapse point (acceleration yc) and the damage starting point (acceleration yi) of the building (Fig. 10). Thus, the curve is obviously undetermined, but it could be adequately represented by a linear conventional trend.
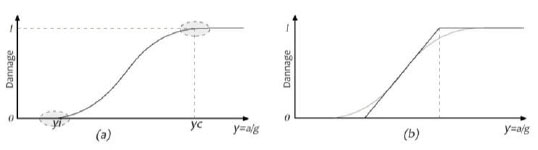
6. RESULTS AND DISCUSSION
The analytical procedure defines, according to the variation of the seismic intensity, the structure probability of reaching or exceeding a particular limit state. In mathematical terms, this is expressed by the conditional probability function P[SL|I], where SL|I is a symbol indicative of achieving or exceeding the assigned limit state when the seismic intensity value (I), which can be represented under form of PGA, spectral acceleration, etc, is fixed.
The ways to define the damage thresholds are numerous: one of these is defined as a function of the two points representative of the pushover curve, that is the yielding displacement Dy and the ultimate one Du [23]. The approach proposed in this paper, instead, correlates the limit states at appropriate drift values, in line with the provisions of other scientific researches on the same topic [18]. As a seismic parameter (intensity measure I) the spectral displacement Sd has been adopted, because the capacity curves have been converted into the ADRS format in order to be able to compare in an easy manner the capacity values with those of the seismic demand represented by the response spectrum. As a result, the fragility curves are obtained mathematically using the following equation:
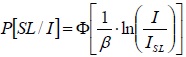 |
(1) |
The equation (1) defines the probability of occurrence or exceeding the limit state considered by means of a log-normal cumulative distribution, where:
- − Φ is the standard normal distribution function;
- − I is the measurement unit of the intensity (or intensity measure);
- − ISL is the median of the intensity measure for which the building reaches a given limit state;
- − β is the standard deviation of the intensity natural logarithm for the limit state considered, assumed equal to 0.6 according to the indications reported in Basoz and Mander [24].
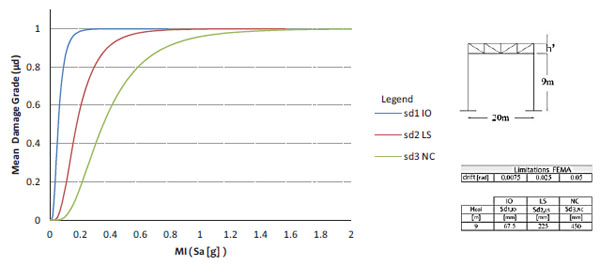
According to this method, each fragility curve is characterised by two parameters: the first is the average value of the intensity measure responsible of reaching the limit state threshold and the second parameter is the relative standard deviation. For each structural system it is possible to trace more fragility curves, each of them associated to a predetermined limit state. An example of fragility curves constructed according to the previous analytical procedure is reported in Fig. (11), where for the same structural system examined with the discretised procedure (case AE2) three curves obtained for three different limit states (IO, LS and NC) are simultaneously reported.
In order to make a comparison between the results obtained by the two methods a sensitivity analysis is performed for defining the value of the standard deviation parameter β, which incorporates all aspects of uncertainty inherent with the determination of the demand, of the capacity curve and of the damage limit states dependant on the structural ductility. Different values of β (0.6, 0.8 and 1.0) have been considered in order to assess the validity of analytical fragility curves to adapt themselves more or less to those curves obtained by using the discretised procedure that, referred to the structure capacity curve, estimate more precisely the expected damages caused by an earthquake. The comparative study, reported in Fig. (12), shows that the curves obtained according to the analytical procedure by assuming β = 0.8, although similar to those obtained with the discretised procedure (vulnerability curves), are not on the safe side because they reach the collapse for acceleration values higher than those obtained with β = 0.6. Therefore, the value of β which is closer to the results obtained with the discrete procedure is 0.6. However, further developments are still needed for more accurate estimates of the value attributed to this parameter, even considering that this study is only the preliminary part of a larger study aimed at pointing out the fragility curves of the entire heritage of industrial steel buildings in Italy.
Later on, the seismic safety of structures examined, placed for the sake of example in Mirandola, one of the sites most affected by the Emilia-Romagna earthquake, has been assessed and, finally, the reliability of the fragility curves deriving from literature analytical formulations has been proved. As regards to the first aspect, it is noticed that, at the Life Safety limit state, the structures, although designed for vertical loads, meet the safety requirements of the current regulations for seismic-resistant structures. In fact, they reach the collapse under an acceleration value greater than that of the seismic zone with the greatest intensity, which is characterized by a peak ground acceleration of 0.35g.
On the other hand, with reference to the second key question, the discrete fragility curves are manually defined according to a procedure much more laborious than the analytical one, the latter requiring the knowledge of a smaller number of factors to more practically assess the safety of structures.
The comparisons highlight that the analytical curves show values of expected damage greater than the values obtained by discrete curves. Therefore, they predict the structural behaviour in a safe way, allowing also to estimate the collapse, by means of a standard deviation parameter set equal to 0.6, with the same acceleration value detected by the mechanical procedure.
In conclusion, from the analysis carried out for individual case studies with h = 9 m, it has been possible to define capacity and fragility curves which, although generalised, can be regarded as a valuable aid in the design and structural verification phases (Fig. 13). In this way, with initial data regarding dimensional and typological aspects, it is possible to estimate in advance the capacity and the structural seismic damage that may affect the Italian industrial structures without conducting sophisticated analyses in the non-linear field.
CONCLUSION
In the paper the problem of the seismic vulnerability evaluation of one-story steel buildings for industrial use, a building typology widespread all over the Italian country, has been discussed. These buildings, although they have demonstrated a good behaviour under recent earthquakes with limited damages and rare cases of collapse, represent a structural typology at risk. The seismic risk is, in fact, very high, since there are many structures of this typology that either were not designed in compliance with anti-seismic regulations or are located in areas subjected to a recent seismic re-classification. Moreover, in case of industrial buildings the problem of safeguarding the human lives is associated with that of safeguarding the values exposed to risk (equipment, manufactured and semi-finished products stocked in the warehouses, etc.). Therefore, the possibility to have seismic vulnerability and risk evaluation models is certainly a great importance aspect aiming at mitigating the collapse seismic risk of these types of structures.
The non-linear analyses carried out in the paper in order to determine the capacity and the fragility curves of a set of steel one-storey building typologies, which are widely spread on the Italian country, have led towards the following conclusions:
- The seismic action has a little influence on design of industrial steel structures: they are more influenced by wind loads rather than those deriving from earthquake.
- The structures, although are designed for gravity loads only, have demonstrated a good behaviour under earthquake. In fact, they reach the collapse for an acceleration value higher than 0.35g, that is the maximum value of the PGA for the highest Italian seismic hazard area.
- The analytical fragility curves overestimate the damage predicted by the discretised vulnerability curves. Thus, they are a method on the safe side in forecasting the steel industrial building collapse under seismic actions.
- The value of the standard deviation parameter β used in the analytical procedure for plotting fragility curves to be adherent to those derived from the discretised method is 0.6. This result is very encouraging, since the same value was also found from authoritative indications provided in literature.
The performed analyses, although they have provided interesting considerations about the seismic hazard of the steel one-storey industrial buildings investigated, represent only the first step towards the seismic vulnerability evaluation of this structural typology. As a consequence, additional analyses will be carried out by taking into account the variability of both the gravity loads and the steel grades used, as well as the change of some additional geometric parameters of inspected structures, for having a more wide knowledge of the seismic vulnerability and fragility of steel industrial buildings.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.


