All published articles of this journal are available on ScienceDirect.
Effects of Bonded Tyres on Leachate Recirculation of Bioreactor Landfills
Abstract
Introduction:
In bioreactor landfills, leachate recirculation significantly influences the process of stabilization and the stability of slope.
Method:
To speed up the leachate recirculation and reduce its adverse impact on slope stability, this paper proposes a new method which constructs a spatial net consisted of bonded whole tyres in the municipal waste during landfilling.
Results and Conclusion:
In this study, a numerical two-permeability flow model was used to investigate the effects of tyres embedding on the outflow rate of leachate injection. Furthermore, it was coupled with momentum balance equations to determine the local factor of safety of slope stability. The established model was applied to a simplified bioreactor landfill. The simulation results demonstrated that the tyre net can accelerate the rate of leachate injection and contribute to distribute the liquid more uniformly. Meanwhile, the slope stability was improved due to the enforcement of waste in the presence of tyres.
1. INTRODUCTION
Recently, bioreactor landfills have been used for the safe disposal of municipal solid waste (MSW) as a new and effective method [1,2]. In bioreactor landfills, the collected leachate is recirculated into the MSW to increase the moisture and accelerate the biodegradation of the MSW [3-8] eventually. There exist many leachate recirculation systems in bioreactor landfills, including vertical wells (VWs) [9-12], horizontal trenches (HTs) [13-17] and drainage blankets (DBs) [18, 19]. Both whole and shredded tyres are commonly employed to form leachate drainage layers, but it remains an controversial issue regarding whether the self-ignition can occur for the scrape tyres in a leachate trench [20]. However, it is clear that reduction in tyre-filled layer thickness and creation of firebreaks are beneficial to avoid a potential combustion of tyres.
To distribute the liquids within a landfill in a desired time period, leachate is usually operated with pressure [21]. However, high injection pressures in leachate recirculation systems near the side slopes can cause excess pore water pressures. The positive pore liquid pressure is prone to reduce the shear strength of the MSW because of the decreasing effective stress, which poses a concern of slope instability.
In this study, a spatial net consisted of bonded whole tyres is proposed to be embedded in the municipal waste during landfilling. The inter-connection between tyres is expected to provide additional flow paths for the leachate and enhance the slope stability due to the effect of enforcement. Meanwhile, the new pattern of disperse tyres leads to thinner drainage layers compared with traditional scrape tyre trenches and consequently reduces the risk of subsurface fires. To reexamine the new concept of drainage system, a two-permeability mathematical model was coupled with momentum balance equations and was used to numerically simulate the leachate flow within a bioreactor landfill subjected to a pressured leachate injection. The simulation results demonstrated that the spatial tyres net significantly enhanced the distribution of leachate and improved the slope stability as well.
2. METHOD
2.1. Leachate Flow Model
The Richards’ equation is employed to describe leachate flows in waste without tyres. The dual-permeability model couples two Richards’ equations to describe the flow within waste matrix and the preferential flow at the tyre-waste interfaces respectively. The two flow domains are considered to be overlapped and interacted. Composite bulk soil properties are composed of domain-specific matrix and fracture pore system properties as [22]:
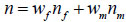 |
(1) |
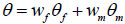 |
(2) |
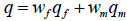 |
(3) |
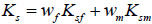 |
(4) |
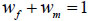 |
(5) |
where the subscript “f” indicates the preferential flow domain and the subscript “m” indicates the matrix domain, n is porosity(L3L-3), θ is the water content (L3L-3), q is the fluid flux density(LT-1), Ks is the total saturated hydraulic conductivity, and w is the volumetric ratio of the preferential flow domain or the matrix domain over the total soil volume (-). Flow of water in the dual-permeability medium is described by means of two coupled Richards’ equations as follows:
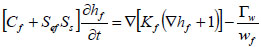 |
(6) |
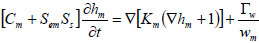 |
(7) |
Where, C is the differential water capacity (dθ/dh) (L-1), Se is the effective saturation, h is the pressure head (L), t is time (T), K is the hydraulic conductivity (LT-1), Ss is the specific storage (L-1), Γw is the water exchange term (T-1) between the two domains.
The van-Genuchten function is used to describe the hydraulic properties of both the matrix and preferential flow domains [23]:
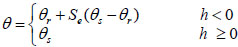 |
(8) |
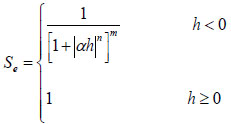 |
(9) |
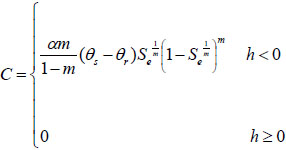 |
(10) |
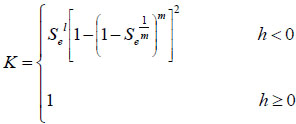 |
(11) |
Where, θ is the water content (L3 L-3), θr is the residual liquid volume fraction, θs is the saturated liquid volume fraction, K is the relative permeability, α, l, m, n are fitting parameters.
Exchange of water between the matrix and the fracture pore systems is assumed to be proportional to the pressure head difference between both pore systems [24]:
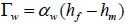 |
(12) |
in which, αw is a first-order mass transfer coefficient (L-1T-1) for water defined as:
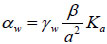 |
(13) |
Where, β is a dimensionless geometry coefficient for describing the shape of the matrix structures, a is the characteristic length of the matrix structure (L), γw is a dimensionless scaling coefficient for water absorption, Ka is the relative hydraulic conductivity. A single average value of 0.4 for γw was found to be applicable for different hydraulic properties and initial conditions [25]. The geometry coefficient β equals 3 [26]. The relative hydraulic conductivity Ka is calculated by averaging the hydraulic conductivities of the two pore domains [27, 28]:
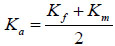 |
(14) |
2.2. Slope Stability Analysis Method
The limit-equilibrium methods are commonly used for slope-stability analyses because of their proven effectiveness and reliability [29-35]. The slope-stability analyses of this study are based on the local factor of safety approach [36, 37]. The total stresses in the linear elasticity model are calculated by a momentum balance equation:
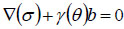 |
(15) |
Where, σ is a stress tensor (ML-1T-2) with three independent stress variables in two-dimensional space, and γ is the bulk unit weight (ML-2 T-2), which is a function of water content θ. b is the unit vector of body forces with two components.
The effective stress can be expressed as [38]:
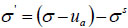 |
(16) |
Where, ua is the pore air pressure, σ′ is the effective stress, and σs is defined as the suction stress characteristic curve of the soil with a general functional form of
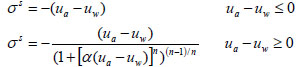 |
(17) |
Where, uw is the pore water pressure,α and n are unsaturated soil parameters identical to those in van Genuchten’s soil-water characteristic curve model.
The local factor of safety (LFS) is defined as the “ratio of the Coulomb stress of the potential failure state under the Mohr–Coulomb criterion to the Coulomb stress at the current state of stress” [36, 37]:
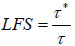 |
(18) |
Where, τ* is the potential Coulomb stress and τ is the current state of Coulomb stress (ML-1T-2). Application of the Mohr–Coulomb failure criterion gives the local factor of safety at every point in the landfill slope:
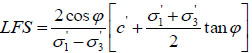 |
(19) |
Where, c′ is the effective cohesion (ML-1T-2), φ is the friction angle, and σ1′ and σ3′ are the spatially varying first and third principal effective stress for the variably saturated soil (ML-1T-2).
2.3. Coupled Dual-Permeability and Soil Mechanics Model
In this study, the Subsurface Flow Module and Solid Mechanics Module in the commercial finite element software COMSOL were used to couple hydrological and soil mechanical system. The two-permeability model is defined as two coupled Richards’ equations and the coupling can be expressed by the water exchange term, which is imported as Mass Source term in the Richards’ Equation Interface. Then, the software solver recognizes the system of coupled equations during the computation. The coupling between the dual-permeability model and soil mechanics model is represented from two aspects. First, the Body Load Term of the Solid Mechanics Module varies with the moisture content; second, the effective stress for Solid Mechanics Module depends on the pore pressure output by the hydraulic module. In this study, there is no experimental data to show the development of slope failure. Therefore, the pore water pressure of the preferential flow domain is used to calculate the effective stress. The framework of coupled dual-permeability model and soil mechanics model is shown below (Fig. 1):
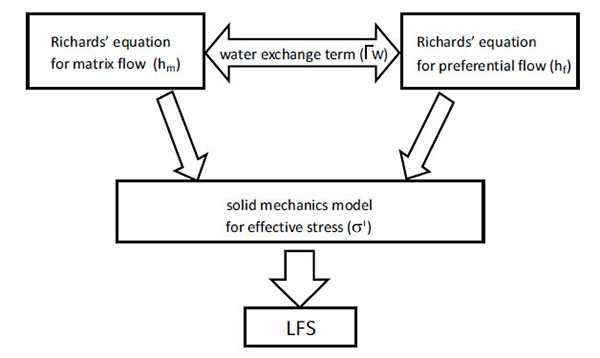
3. APPLICATION TO A LANDFILL PROFILE
The configuration of landfill is similar to that examined previously (Xu et al. (2012)) as illustrated in Fig. (2). The leachate is injected through a horizontal trench into the waste with a continual injection pressure. The leachate collection and removal system (LCRS) is located at the base of landfill with a thickness of 0.3 m and consists of granular material such as sand. The top boundary, left-hand side and side slope are no-flux boundaries. The pore-water pressure of the bottom sides for LCRS is fixed to zero due to the drainage layer. At the horizontal trench, a constant injection pressure is applied. For the solid mechanics model, the side slope is a free boundary, and the top and the left-hand side can move in laterally and vertically, respectively. The bottom boundary is fixed.
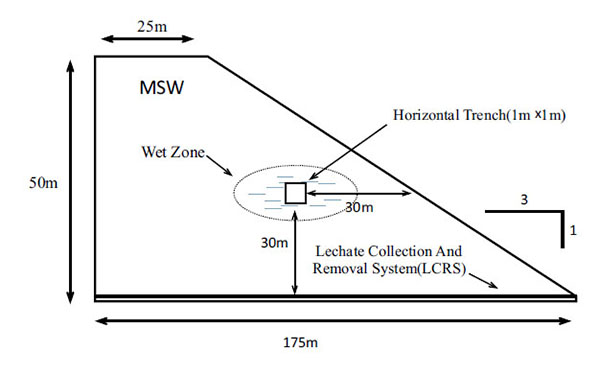
All the parameters used in the following examples are listed in Table 1. In this study, the unsaturated hydraulic properties of the MSW were not varied with respect to the depth because: (1) very little published information is available on the evolution of unsaturated hydraulic properties of MSW as a function of overburden pressure; and (2) unsaturated hydraulic properties have a relatively small impact on the key design parameters at steady-state conditions [39].
| Symbol | Parameter Name | Units | Value |
|---|---|---|---|
| γa | Unit weight | (kN/m3) | 5.5 |
| α | Inver of air-entry pressure | (1/kPa) | 1.4 |
| θr | Residual moisture content | (-) | 0.14 |
| θs | Saturated moisture content | (-) | 0.58 |
| n | Van Genuchten fitting parameter | (-) | 1.6 |
| a | Van Genuchten fitting parameter | (-) | 0.37 |
| b | Van Genuchten fitting parameter | (-) | 0.5 |
| c | Van Genuchten fitting parameter | (-) | 0.5 |
| Kv | Hydraulic conductivity | (m/s) | 1×10-7 |
| Kh/Kv | Waste anisotropy | (-) | 10 |
| C’ | Waste cohesion | (kPa) | 15 |
| C”b | Tire shred-sand mixtures cohesion | (kPa) | 41 |
| Φ’ | Waste friction angle | (Degree) | 35 |
| Φ” | Tire shred-sand mixtures friction angle | (Degree) | 35 |
| p | Injection pressure | (kPa) | 49 |
3.1. Comparison with Previous Work
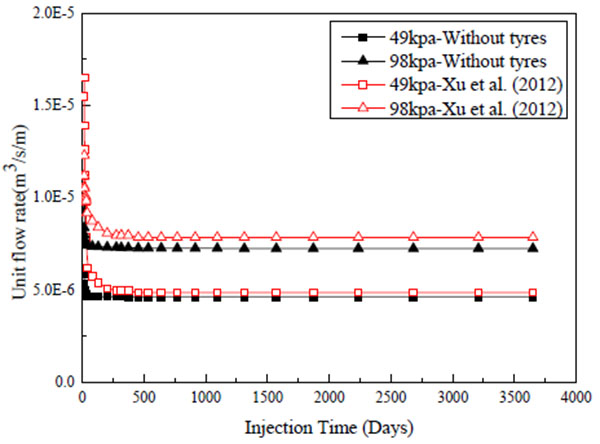
Prior to being applied to landfills, the results obtained from the present computational model were compared with the published results. The evolution of outflow rate with time was determined and was found as satisfactorily close to that of Xu et al. (2012) Fig. (3). To reexamine the influences of preferential flow on slope stability, Shao et al. (2014) performed local factor of safety (LFS) analysis for a slope with rainfall infiltration. Fig. (4) shows the LFS distribution and the results of the model established in this study agree well with Shao et al. (2014).
3.2. Simulation Results and Discussion
3.2.1. The Flow Rate and Distribution of Leachate
A base scenario without tyre was simulated using single-permeability model to determine the influences of varying injection pressures on leachate outflow rate, the distribution of the degree of saturation of leachate and the local factor of slope safety. As for the landfill with spatial tyre net, the two-permeability model was utilized to represent the preferential flow paths created by tyre-waste interfaces.
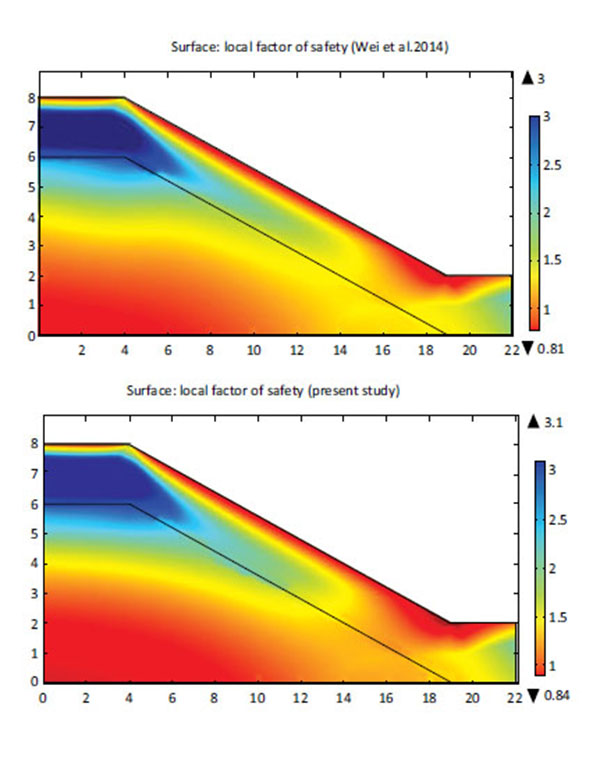
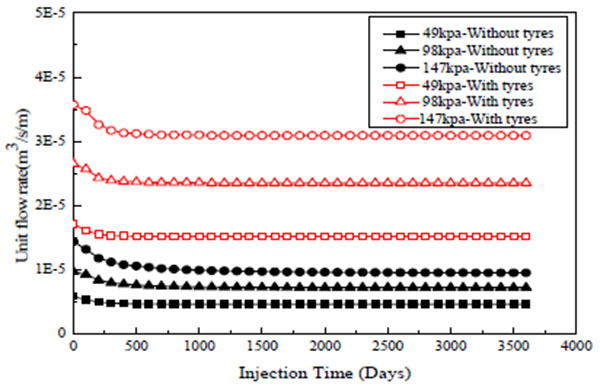
Fig. (5) illustrates the variation of outflow and the presence of tyre net significantly speeds up the leachate injection up to three times. The associated leachate distribution in Fig. (6) demonstrates that the two-permeability model leads to a larger wetted zone than the single-permeability model. Moreover, the wetting front of the landfill with tyre net spreads laterally further rather than going downward to the bottom drainage layer as for its counterpart, which indicates that the tyre net results in a more uniform distribution of leachate. For a bioreactor landfill, the accelerated distribution uniformly is a key desired feature.
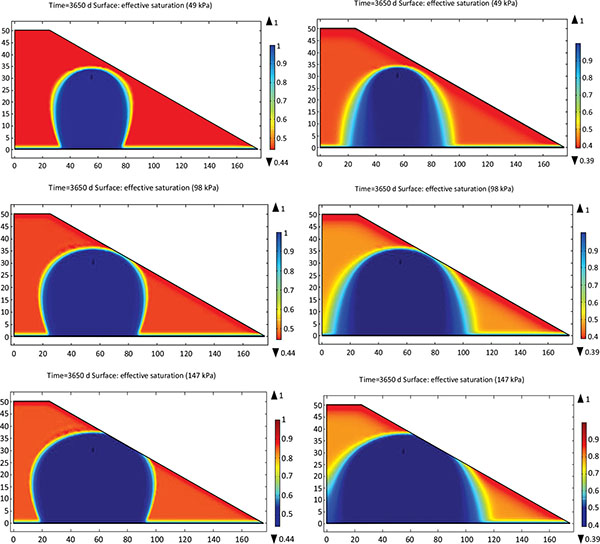
3.2.2. Slope Stability
Tyre has been proven to improve the shear strength of soil in both field and laboratory experiments [33]. It is reasonable to anticipate a similar enforcement for waste in a landfill with tyre. Since the data for enforcement of waste by the whole tyres is scarce, this study represents it by increasing the cohesion and angle of internal friction following the experiments in Zornberg et al. (2004).
The distribution of local factor of safety is illustrated in Fig. (7). The LFS becomes smaller when the wetting propagates because the effective stress becomes smaller due to the increasing liquid pressure. For the cases with a lower injection pressure (49 and 98 kPa in the considered scenario), the LFS is larger than unity and it indicates no slope failure. However, the LFS decreases to 0.83 around the horizontal trench for injection when the injection pressure changes to 147 kPa. In the presence of tyre net, the LFS increases especially along the slope face due to the improvement in shear strength, consequently avoiding the potential occurrence of slope slide.
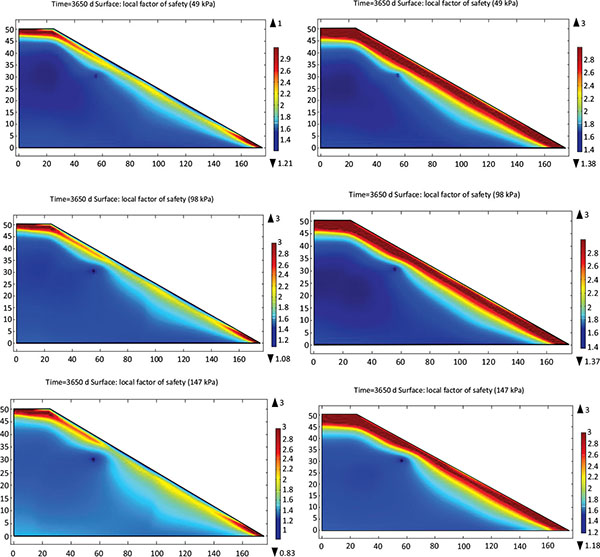
CONCLUSION
This paper proposed to use a spatial bonded whole tyre net to accelerate the leachate recirculation in bioreactor landfills. A two-permeability flow model was employed to represent the preferential flow at tyre-waste interfaces and the flow within waste. Additionally, the flow model was coupled with solid mechanic model and by which the local factor of safety was determined. In this study, the established model was applied to a landfill and it demonstrated that the tyre net can significantly speed up the leachate injection and the liquid was distributed more uniformly. Furthermore, the slope stability was improved due to the enforcement of waste by virtue of tyres.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Funding for this study was provided by the National Natural Science Foundation of China (Grant No. 51308259), the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (Grant No. 13KJB610004), and the Foundation for Advanced Talent of Jiangsu University, PRC (Grant No. 13JDG060 and No. 14JDG023). The valuable suggestions from Dr. Shao Wei, Faculty of Civil Engineering and Geosciences, Delft University of Technology, are sincerely appreciated.


