All published articles of this journal are available on ScienceDirect.
Simulations of Local Scour Around a Cylindrical Bridge Pier And a Semicircular Abutment Using Unsteady k-ε Model Combined with σ-Grid
Abstract
Introduction:
Bridge scour is one of the major causes of bridge failure. Prediction of the maximum depth and shape of local scour plays an important role in bridge design and maintenance. In this paper, k-ε turbulent model combined with wall function was employed and complex flow fields are exhibited. The bed load transport model summarized by Qian and Wan [1] was applied to evaluate the development of local scour. Besides, σ-grid module was developed and embedded into the commercial solver FLUENT to fit the change of channel-bed.
Method:
In this module, the change of the elevation of the channel bed is calculated through using user defined functions(UDF), and the motion of the grid system is realized based on a program developed through C++ language, which extends the applications of FLUENT. The evolution of local scour hole for two cases, i.e., local scour around a cylindrical pier and a semicircular abutment, was simulated.
Results and Conclusion:
The depth and the shape of local scour as well as the flow fields were predicted. Numerical result conforms well to the experimental measurement. Especially, it provides fairly reasonable prediction on the key issue of the maximum scour depth. The satisfactory agreement validates the numerical method developed in the present study. In addition to the validation purpose, the different performance of this method for predicting local scour around the cylindrical pier and the semicircular abutment was discussed.
1. INTRODUCTION
Sediments on the channel bed interact with energetic coherent vortex structures leading to local scour which could undermine the structural reliability of embedded hydraulic structures and endanger the channel bed stability. For bridge engineering, local scour around bridge piers or abutments is commonly recognized as one of the major causes of bridge failures at river crossing. Local scour has led to massive lose on life and economy, and resulted in serious impact on local transportation as pointed out by Shepherd [2]. Therefore, the prediction of local scour especially the maximum depth of scour hole, is critical for bridge design, maintenance and evaluation. Over the past decades, many experiments have been conducted to study this issue as Yanmaz [3], Ettema [4], and Sheppard [5, 6]. However, the detailed vortex structure is difficult to be revealed based on experimental measurements. In addition, there are also several scour equations based on laboratory data but they did not always produce reasonable results according to Chavan [7]. In this context, Gaudio et al. [8, 9] showed that due to different mathematical structure of empirical formulas, different results may be obtained through using scour depth predictive equations. Numerical simulation is another approach to examine the flow structure in the hole of local scour or the development of local scour. In the present study, the numerical approach is adopted. The numerical simulation concerning local scour could be grouped in two types. One type is the fixed bed simulation, the other is the movable bed simulation. In the following, we briefly review these two types of simulations.
Due to the fact that there is no variation of the elevation of river bed, the computation for flow fields over the fixed bed is not as useful as the live-bed case. Therefore, we can use more accurate turbulent models to study this issue, such as large eddy simulation (LES). Zhao and Aode [10] applied LES turbulent model to examine the flow fields and the scouring mechanism around a circular pier. They found that at the downstream of the pier, when the scouring depth increases, the turbulent intensity as well as the pressure fluctuation increases. Besides, the bed shear stress at the upstream of the pier is primarily influenced by the horseshoe vortices. Pasiok and Stilger [11] investigated the mass particle trajectories around a pier through large eddy simulation and concluded that the particle trajectories depend on intensity of vertical vortices which is the main driving force moving the particles out of the scour hole. Bressan et al. [12] applied large eddy simulation to examine the turbulent flow around a scoured bridge abutment and concluded that the dynamics of the primary vertical structure can induce large shear stress on the bed, leading to sediment transport to be highly intermittent. Kirkil and Constantinescu [13, 14] studied the flow and turbulence structure around an in-stream rectangular cylinder and a spur dike with scour hole on the basis of detached eddy simulation (DES). In the studies, they highlighted the need to understand and differentiate the mechanisms causing scour around bluff body obstacles of different shapes and at different stages of the scour process.
For the movable bed simulations, currently, there are three approaches. The first one is to consider the sediment and water as two phases. The second approach is based on the bed shear stress and the sediment transportation model and the last is based on smoothed particle hydrodynamics (SPH) model.
For the first approach, Richardson et al. [15] applied the two-phase flow modeling techniques and simulated the flow structures around a bridge pier with and without the scour hole. Compared the simulated results with the experiment ones, they found that the FLOW3D hydrodynamic model well simulates the complex flow patterns around the bridge pier. Huang et al. [16] applied two-phase Eulerian model to simulate the local scour progress. They examined the scale effects on sediment scour and found that ignoring Reynolds similarity in physical modeling may result in errors for scour in large bridge piers. However, two-phase model will increase the number of governing equations, thus definitely increasing the computing time.
For the second approach, Zhao et al. [17, 18] employed a three-dimensional finite element numerical model to simulate the local scour around submerged vertical cylinders. k-ω turbulence closure was applied to solve the URANS equations and found that the horseshoe vortex combined with the other vortices governs the scouring process. Abdallah et al. [19] applied SSIIM program and solved Reynolds-stress term by k-ε model, indicating that the curvature shape of bridge abutment could reduce the local scour depth by more than 95%. Ehteram and Meymand [20] selected SSIM2 code to model the scour depth at side piers of the bridge. They found that the SSIM2 model slightly underestimates the scour depth but overall the results from SSIM2 are acceptable. Basser et al. [21] applied SSIIM 2.0 to model the scour around a rectangular abutment. SSIIM 2.0 employs k-ε turbulence model with some RNG extensions for predicting the turbulence. It could be concluded that SSIIM 2.0 numerical modeling is capable of simulating scour around the rectangular abutment. Xiong et al. [22] used commercial software FLUENT together with the dynamic mesh available in FLUENT to simulate the local scour around bridge piers. However, the tetrahedral mesh with quite large size was applied near the bridge piers and the channel bed which will influence the accuracy of the prediction of local scour depth.
Mirmohammad and Ketabdari [23], Ran et al. [24] presented the method simulating local scour by SPH model. However, up to now, in the most commercial solvers, the SPH model has not been integrated, limiting the applications.
In the present study, the commercial code FLUENT (Fluent 6.3, Fluent Inc.) was extended by user defined functions (UDFS) to make the function of modeling local scour with structured mesh available in it. The block structured mesh will be used with very fine mesh close to the pier and the channel bed. The second numerical approach such as solving the sediment continuity equation, was employed and the change of topography was fitted by σ grid technique. Two cases (cylindrical pier and semicircular abutment) will be examined to verify the model developed. In addition, the different scour patterns between them are also discussed.
2. NUMERICAL METHOD
The governing equations are introduced in section 2.1. Section 2.2 and section 2.3 present the sediment transportation model and the σ grid respectively, followed by the presentation of the boundary conditions used in this study.
2.1. Governing Equations
The turbulent flow is simulated by solving the Unsteady Reynolds-Averaged Navier-Stokes (RANS) equations with a k-ε turbulence model. The Arbitrary Lagrangian Eulerian (ALE) scheme was employed for solving the RANS in a computational domain with continuously developing bed boundary. In the ALE scheme, the position of each mesh node moves and convection terms are modified to consider the effects of the mesh moving speed. According to the FLUENT 6.3 User’s Guide [25] the URANS are expressed as:
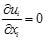 |
(1) |
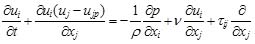 |
(2) |
in which, xi (i=1, 2, and 3) is the coordinate along axis in Cartesian coordinate system, ui is the instantaneous velocity component in xi direction; ρ is the density of clear water; t is time; ujp is the velocity of the movement of the computational mesh; ν is the kinematic viscosity; τij is the Reynolds stress defined as τij = νt(∂ui/∂xj + ∂uj/∂xi)−(2/3)kδij; νt is the turbulent viscosity; k is the turbulent kinematic energy and defined as k = 1/2u'iu'i; u'i is velocity fluctuation in xi direction. The standard k − ε turbulent model is employed to close the RANS. For the standard k − ε turbulent model, turbulent kinetic energy k and turbulent dissipation ε rate are obtained based on the following transport equations:
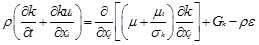 |
(3) |
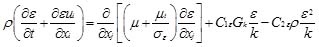 |
(4) |
where
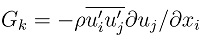 represents the generation of turbulence kinetic energy due to the mean velocity gradients; μt = ρCμk2 / ε; C1ε, C2ε, Cμ, σk, σε are the empirical constants, with value of C1ε = 1.44, C2ε = 1.92, Cμ = 0.09, σk = 1.0, σε = 1.3 in this study.
represents the generation of turbulence kinetic energy due to the mean velocity gradients; μt = ρCμk2 / ε; C1ε, C2ε, Cμ, σk, σε are the empirical constants, with value of C1ε = 1.44, C2ε = 1.92, Cμ = 0.09, σk = 1.0, σε = 1.3 in this study.
In standard k − ε turbulent model, the flow is assumed to be fully developed turbulent flow. In order to avoid fine grids among sub-layer and save computational time, wall function is applied to obtain wall sheer stress. It can be done by using:
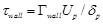 |
(5) |
In which subscript “p” stands for the center of control volume adjacent to wall; Up is the velocity component parallel to the wall; δp is the distance from the center of control volume to the wall; Γwall is the dissipation constant and can be obtained from the following equation:
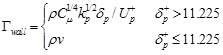 |
(6) |
where
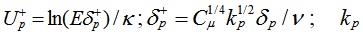 is turbulence kinetic energy at point “P”; κ is the Karman constant. Gaudio etc. [26] argued that the Kármán constant is however nonuniversal in flows over mobile sediment beds. Besides, Foken[27], Hogstrom[28, 29] report values of κ between 0.35 and 0.42. Following the study by Fuhrman[30]. 0.4 is chosen for the Karman constant. E = eκ(B−ΔB) is the roughness empirical constant; B= 5.2 is additive constant; ΔB is the roughness function which reads as follows:
is turbulence kinetic energy at point “P”; κ is the Karman constant. Gaudio etc. [26] argued that the Kármán constant is however nonuniversal in flows over mobile sediment beds. Besides, Foken[27], Hogstrom[28, 29] report values of κ between 0.35 and 0.42. Following the study by Fuhrman[30]. 0.4 is chosen for the Karman constant. E = eκ(B−ΔB) is the roughness empirical constant; B= 5.2 is additive constant; ΔB is the roughness function which reads as follows:
 |
(7) |
In which ks+ = u*ks / ν is the effective roughness height of the wall boundary or particle Reynolds number playing an important role in quantifying the influence of roughness on the bed and solid boundaries. For the stationary flat bed with uniform grain size, ks should be equal to the median grain size, d50. At present, a value of ks = d50 for the bed is employed.
2.2. Sediment Transportation Model
The scour problem is due to the movement of the channel bed sediments. Bed materials that are transported along the bed are called bed load. Bed load moves by rolling, sliding, and hopping. However, if particles settle down slowly enough and are carried in current either never touching the bed or only intermittently touching it, they are treated as suspended load. The scouring type, i.e., bed load and suspended load, depends on the size of particles and flow velocity. If the average diameter of the particles is larger than the critical diameter, sediments will be transported in the form of bed load. Otherwise, suspended load will be the main transportation form. The critical diameter of particles can be obtained by the equation provided by Qian and Wan [1] as:
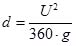 |
(8) |
where U is the mean approaching flow velocity; d is the diameter of sediments. In this paper, the mean approaching flow velocities for the bridge pier case and abutment case are 0.25m s-1 and 0.294m s-1, with sediments average diameter of 0.385mm and 0.52mm respectively, which is significantly larger than the corresponding values of U2 / (360⋅g). As a result, bed load is considered as the main transportation form. Such physical processes are governed by the sediment continuity equation combined with the bed-load transport equation. We applied herein the bed morphodynamic model summarized by Qian and Wan [1]. According to sediment transport balance, the variation of bed elevation can be derived as:
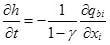 |
(9) |
where γ is the sediments porosity; h is the elevation of the channel bed; and qbi represents the bed load flux vector in the xi direction. If we know the bed load flux at each time step, the variation of the channel bed elevation could be calculated using Eq.(9). Explicit Euler scheme is chosen to solve Eq(9), indicating that the renewed elevation of channel bed is calculated using the information of the flow fields at the previous time step with the consideration of the easy of programming. If implicit scheme is applied, during iterations not only the flow fields will be renewed by the grid coordinates which bringing much more difficulties. In the future, we will attempt to use more accurate implicit schemes to solve the N-S equation as well as the sediment transportation equation at the same time. In fact, an accurate prediction of the bed load flux plays a critical role in correct estimation of scour depth variation. Recently, Dodaro et al. [31, 32] modified Einstein bed load equation to predict local scour downstream of a rigid bed. In the present study, bed load flux was estimated as follows. Considering the slope of channel bed, Eq.(10) is adopted to determine qbi following the study by Qian and Wu[1]:
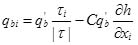 |
(10) |
in which τi is the bed shear stress in xi direction; |τ| is the magnitude of the bed shear stress; C = 1.5 an empirical constant following the study by Qian and Wu[1]; h is the bed elevation; q'b is determined from:
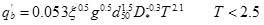 |
(11) |
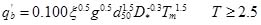 |
(12) |
in which diis the diameter sediment whose weight is less than i% of all sediment; ξ = (ρs − ρ) / ρ is dimensionless density; ρs is the sand density; g is the gravitational acceleration 9.8m s-2; D* = d50 [(s − 1)g / ν2]1/3 is the dimensionless particle parameter; s = ρs/ ρ is the relative density; T is the non-dimensional excess bed shear stress; and Tm is the modified non-dimensional excess bed shear stress; T and Tm are expressed as:
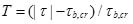 |
(13) |
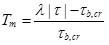 |
(14) |
where λ = e(0.45α + 0.2β) is correction factor; α = 1 − σg; β = d50 / d90 − d10 / d50; σg = (d84 / d50 + d50 / d16)/ 2; τ is the shear stress
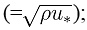 u* is the shear velocity; τb,cr is the critical bed-shear stress at which sediment starts to move. For the local scour problem, Qian and Wan [1] presented a formulation of critical sheer stress considering the effects from the bed slope:
u* is the shear velocity; τb,cr is the critical bed-shear stress at which sediment starts to move. For the local scour problem, Qian and Wan [1] presented a formulation of critical sheer stress considering the effects from the bed slope:
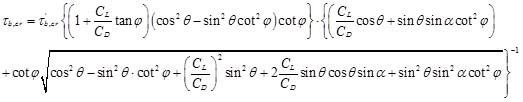 |
(15) |
where φ is the angle of repose for sediments; CL donates the lift coefficients for the particle; CD is the drag coefficients for the particles; CL/CD=0.85, as indicated by Ye and Wen [33]; α is the angle between the flow direction and the slope direction projected onto a horizontal plane; θ is the angle between the slope and horizontal plane, as shown in Fig. (1). τ'b,cr is critical bed-shear stress for sediments on horizontal bed and can be obtained by:
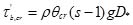 |
(16) |
in which θcr is the Shields number, which can be obtained from the shields curve. The sediment transportation model presented above is coded using user defined functions in FLUENT.
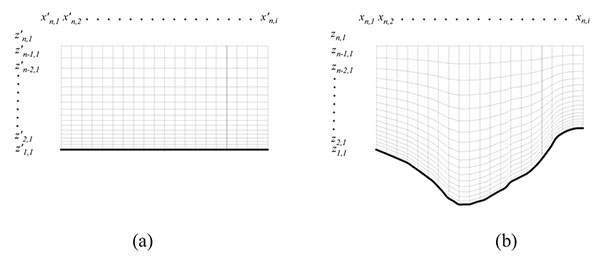
2.3. σ-Grid
For the live-bed calculations, the topography of the channel bed changes with time. Therefore, in order to fit channel bed at each time step a novel adaptive grid method, σ adaptive grid is applied. The basic philosophy of the method can be summarized as follows. In the σ adaptive grid system, the ratios of the neighboring grid sizes hold as constants. An example of two dimensional σ adaptive grid system can be found in Fig. (2a and 2b). Fig. (2a) shows the grid at the stage without the variation of the elevation of the channel bed and Fig. (2b) is with the variation. It could be found that the total grid number and the horizontal grid size do not change before and after scouring. What changed is only the grid coordinates in the vertical direction but the ratios of the neighboring grids hold as constants. In this way the variation of the channel bed topography is fitted quite well. The σ adaptive grid is not available in FLUENT. Therefore, with the intent to apply σ adaptive grid, we extended FLUENT using language C++ which could control the running of FLUENT and read or change the node coordinates at each time step. The time step size is set as 0.001s. Several time step sizes have been examined and found that the numerical results will be independent with the time step size when it is smaller than 0.001s.
The procedure in the calculations was as follows:
Step 1. generate the mesh using Gambit;
Step 2. calculate the flow;
Step 3. calculate the sediment transport;
Step 4. calculate the variation of channel bed elevation;
Step 5. update the channel bed using σ-grid;
Step 6. return to Step 2.
2.4. Boundary Conditions
The computational domain includes boundary conditions of inflow, outflow, symmetry boundaries and walls.
2.4.1. Inflow and Outflow
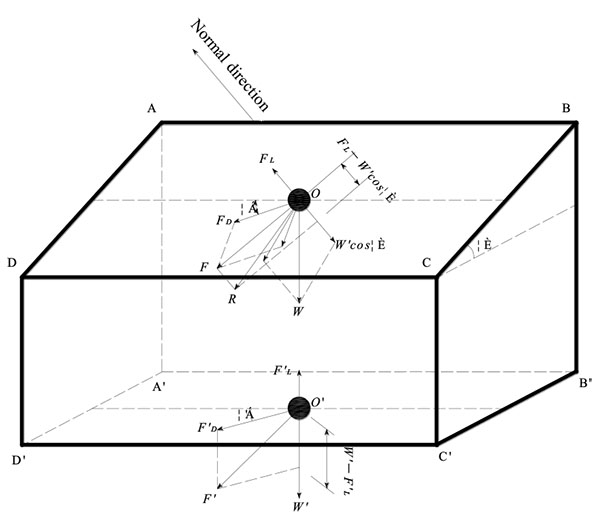
For each inlet boundary, Dirichlet boundary condition as has been introduced in detail by Ferziger (2002) is given and the transverse as well as the vertical velocity components are set to be zero. In each case, a separate calculation of flow in a straight channel of a length of 20D (diameter of the pier or abutment) is carried out whose inlet velocity is determined by U = Q / A, where Q is the water discharge and A is the wet cross-section area, and turbulent kinetic energy k as well as turbulent dissipation rate ε at the inlet are 0 respectively. The velocities as well as the turbulent quantities at the outlet boundary of the straight channel are used as the inlet boundary for scour simulation. This is a reasonable way to produce a stable boundary layer flow condition constituent to the rough riverbed and the turbulent model used. At the outlet boundary, the Neumann conditions were applied. The gradients of the velocity and the turbulent quantities (∂ / ∂n) in the flow directions are set to zero and the reference pressure of zero is provided. We did not specify the velocity values at the outlet. The flow depth is constant for all of computational domain. Multiphase technique could be used to calculate the free surface. However, due to the limited computational resource, we finally decide to use the symmetry boundary condition for the modelling of free surface, so the water depth is a constant.
2.4.2. Symmetry and Wall Boundaries
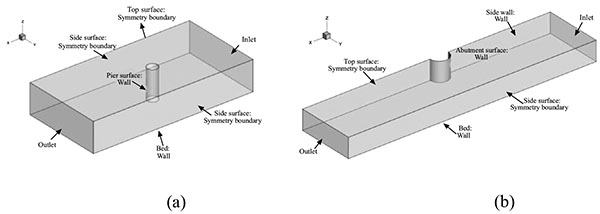
At two side boundaries for the pier case, one side boundary for the abutment case as well as the top boundaries for both two cases (water surface boundary), as shown in Fig. (3), the velocity component and gradients of other dependent variables in normal direction are set as zero. At the bed for the pier case and the abutment cases as well as the side attaching the abutment, the standard wall function boundary condition is adopted. The logarithmic law considering the roughness on the wall was used and depicted as Eq.(7).
3. NUMERICAL MODELS
3.1. Numerical Models
Two experimental models, i.e. cylindrical bridge pier by Melville [35] and the semicircular abutment by Dey and Karim[36], were numerically modeled.
3.1.1. Cylindrical Bridge Pier
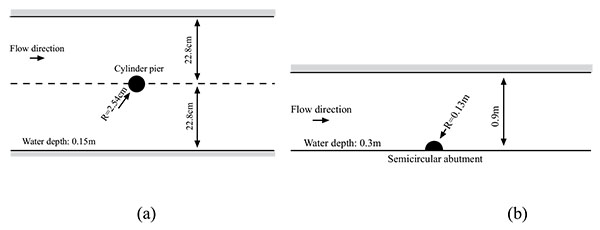
To validate the effectiveness of the present method, numerical simulations of flow and bed deformation around a cylindrical pier are carried out firstly. The simulation condition is almost the same as that performed in laboratory experiments reported by Melville [35]. The tests were conducted in a water flume of 19m long and 45.6cm wide. A cylinder with diameter, D, of 5.08cm was simulated as a bridge pier model. The bed material involved was relatively uniform sized sand with a median grain size of 0.385mm. The approaching mean flow velocity is 0.25m s-1. Water is discharged at the rate of 0.01712m3 s-1 with water depth of 0.15m. Fig. (4a) shows the sketch of the experiment setup. For the computational domain in the numerical simulation, inlet locates at a distance of 7D upstream of the cylinder whose diameter is the same as that in the experiment by Melville (1975). The outlet locates at a distance of 10D downstream the cylinder. The computational domain is 0.15m thick and 45.6cm wide which are identical with those in experiment. The origin point of the domain locates at the center of the cylinder attaching the original channel bed.
For the abtment case, the experiment by Dey and Karim [36] is modeled. That experiment was conducted in a flume with length of 20m, width of 0.9m and depth of 0.2m. A semicircular abutment model with a diameter of 0.26m is located in this flume in which the sand with uniform diameter of 0.52mm is filled to model the channel bed, as shown in Fig. (4b). The water depth at the inlet is 0.2 and the mean flow speed is 0.294 m s-1. As a result, the flow rate is 0.0524 m3 s-1. For the computational domain in the numerical simulation, inlet locates at a distance of 7D upstream of the semicircular abutment. The outlet locates at a distance of 10D downstream. The computational domain is 0.2m thick and 0.9m wide which are identical with those in experiment, as shown in Fig. (4b). And the origin point of the domain locates at the center of the semicircular abutment attaching the original channel bed.
3.2. Mesh System
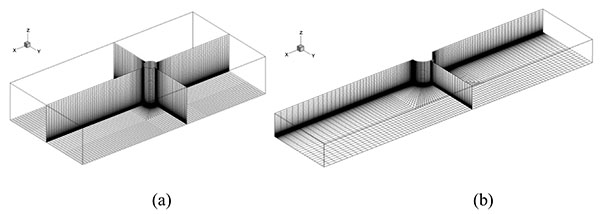
The generation of an appropriate grid has been proved to have a major effect upon model prediction and ideal grid would produce a flow field which is independent of grid dimensions, with as low grid density as possible to save computational time. The computational domain is discretized by multi-blocked structure hexahedral grids. In the region close the walls of the structures (pier and abutment) and the channel bed, the flow is very complex. Therefore, the grids are refined. Near the walls and the ground the first grid layer size is set as 0.2mm(fine), 0.5mm(medium), and 1mm(coarse) to check if the numerical simulation is grid independent through comparing the flow fields of the fixed bed situations obtained from each grid system. It is found that the fine and medium grid systems give almost the same results, indicating that the grid independence requirement is reached at the medium grid stage. In the present study, the results of the fine grid system will be presented. The grid growing ratio is 1.1 to avoid the numerical errors resulting from the sudden change of the mesh. The largest grid size is limited as 2cm. Totally,105948 grids are generated for the calculation of the pier and 201526 for the abutment. The detailed picture of the grid distribution could be found in Fig. (5).
3.3. Solving Schemes
The governing equations are discretized on collocated grid system through using the finite volume method. The second order upwind scheme is used for the convective and viscosity term. The central difference scheme is used for the diffusive term. SIMPLEC algorithm is employed as introduced by Ferziger and Peric [34]. Time step size is 0.001s. The computation was stopped after 30min for the pier case and 60min for the abutment case because the maximum change of the scour hole in between 1min is less than 0.01mm. The computational time is huge. For single simulation, it will cost 7 days on the cluster with 8 nodes and each node consists of 8cores. The floating point speed of each core is 2.4GHz.
4. NUMERICAL RESULTS AND VALIDATIONS
4.1. Cylindrical Bridge Pier
Fig. (6a, b and c) show the grid systems of the bridge pier with scour at 10min, 20min and 30min respectively. In Fig. (6), we would like to show the change of channel bed more clearly; therefore, only 1/4 of total grids are shown. It can be found that σ-grid fits the complicate terrain successfully. At 30min, the topography is most complex and the gradient of the elevation of channel bed gives the maximum value, however, the grid quality is still very good with the maximum skew ratio of only 0.1.
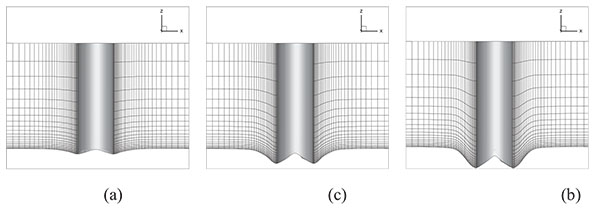
Fig. (7) shows the contour of the scour elevation and the corresponding experimental results. The difference between the computed maximum equilibrium scour depth (approximately 5cm) and the corresponding measured values of 4.2cm is within 25% . A significant qualitative difference does exist between the experiment and the simulation. The former shows a maximum scour region wrapping around the front of the pier and extending up until about 80o angle from the streamwise central line. Nevertheless, the simulation shows that the maximum scour is confined in a small region at the side of the cylinder. This discrepancy should be due to the inherent inability of URANS models to resolve the dynamics of the horseshoe vortex system at the nose of the cylinder which has historically been considered as the main driving force of scour in this region. The horseshoe vortex system will be discussed later in more detail to demonstrate the mechanism of the difference between the simulation and experiment.
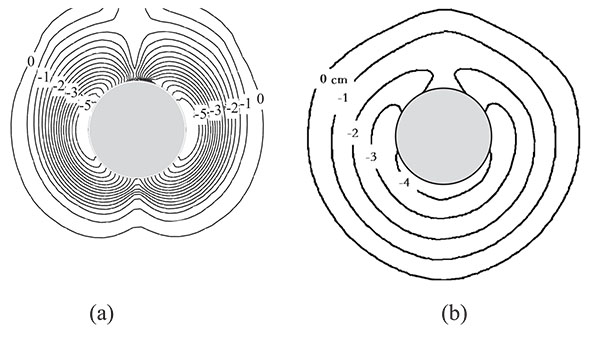
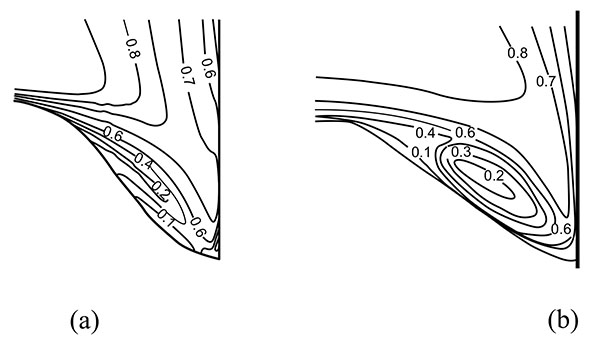
Fig. (8a and b) show comparisons of the distribution of the flow speed on the slice of y=0 between the experiment measurements and the numerical simulations at the equilibrium stage. The data from simulation is time averaged. After the scour reached the equilibrium stage, we stopped the topography calculation but continued the simulation for another 2min. The flow fields at each time step during this 2min are sampled to obtain the time averaged flow fields at the equilibrium stage. The speed is normalized the same as the experiment by the mean approach flow velocity that was 0.25m s-1. In both the simulation and the experiment, it can be found that a strong downward flow developed along the pier face produced rather large velocity components near the bed, which distorted the profiles in the vicinity of the cylindrical pier. Flow separates at the nose of the scour hole and reattaches at the front of the pier, forming a horseshoe vortex, which can be clearly identified from both the simulation and the experiment.
The horseshoe vortex induces high bed shear stress, leading to the suspension of the sediment in front of the cylinder. The suspended sediment is washed away to the downstream of the cylinder by this vortex. Nevertheless, in comparison with the experiment, we can find that the horseshoe vortex does not fully develop and the dimension of the vortex is weakened. In the experiment, the horseshoe vortex reaches to the location just beneath the cylinder, and the vertical size of the vortex is about twice as large as that in the simulation, implying that the URANS model could not resolve the dynamics of the energetic horseshoe system well at the upstream junction of the cylinder with the bed. More sophisticate turbulent model, such as LES (large eddy simulation), and sediment transportation model should be applied in the future.
In fact, LES model has a great ability to resolve vortices. Recently, Calomino et al. [37] successfully simulated small vortices within the macro roughness elements in a corrugated pipe by means of LES model. As a result, it is believed that LES has an acceptable capability to resolve horseshoe vortex around the pier. However, LES model requires larger grid density and smaller time step size which indicates the computational time will increase significantly. We have pointed out that using the 8nodes×8cores cluster combined with the URANS model the computation will last for 7 days. Thus, if the LES model is used, based on the computational resources applicable, now the computation time will increase to at least several months. Therefore, we can conclude that for the numerical prediction of the scour, the URANS model is currently more suitable than LES from engineering application point of view.
4.2. Semicircular Bridge Abutment
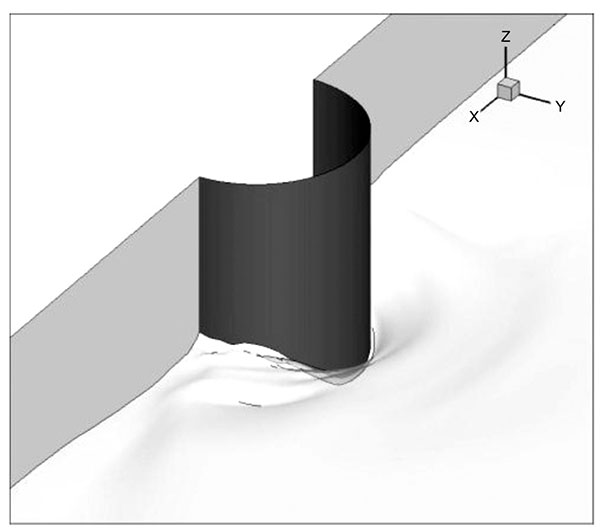
Admittedly, it is the first time to numerically simulate the local scour around a semicircular bridge abutment. Three dimensional view of the simulated scour hole around a semicircular abutment is shown in Fig. (9) with positive x being the inflow direction. It can be found that the scour depth increases as closing the abutment and shows the maximum depth at the lee side, after which the scour depth decreases, proving a reasonable shape of local scour.
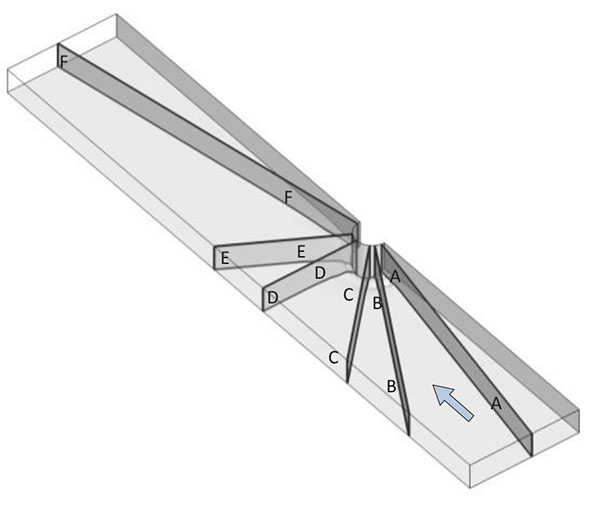
Six slices with azimuthal angle of 10°(A-A), 30°(B-B), 45°(C-C), 90°(D-D), 120°(E-E) and 170°(F-F) same as those in the experiment by Dey and Barbhuiya(2005) are shown in Fig. (10). The profiles of the scour and the flow fields on these six slices will be discussed. In the following discussion, r is the radiation distance from center of the abutment, θ is the azimuthal angle. Same as experiment the vertical coordinate and the radial distance will be normalized by l=D/2.
Different from the previous cylinder pier case, horseshoe vortex system around the semicircular abutment is not developed very well as has been pointed out by Gogus [38]. Therefore, it is reasonable to anticipate that scour in this case should primarily be driven by the bed shear-layers that sheds from the nose of the abutment and locally increases at the lee side.
Besides, it is also anticipatable that the URANS model should be more appropriate for the prediction of the local scour around the abutment. Fig. (11) shows the comparison of the scour hole at the equilibrium stage, from which we can see the simulated results give quite good agreement with experiment. In the simulation the maximum depth of the scour hole, dm, reaches to 153mm which is only 9mm lower than the experiment. The bed elevation patterns are very comparable based on the measurements. In fact, for this case, the simulation captures correctly the location of maximum scour patterns and the overall shapes of the bed elevation contours.
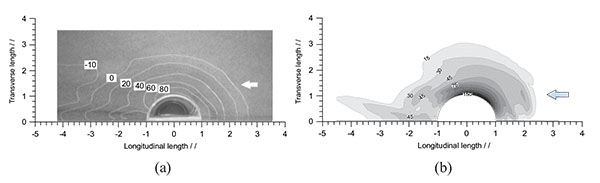
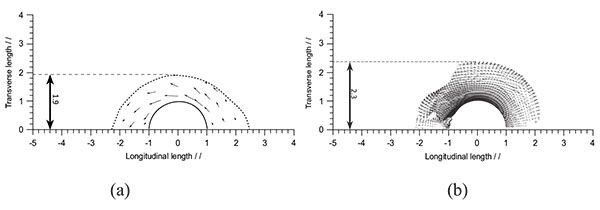
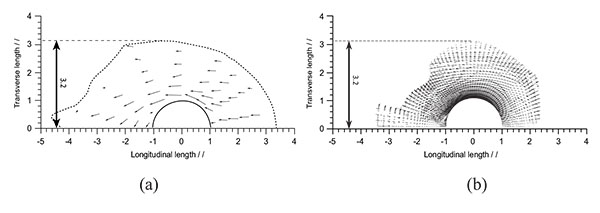
In addition, flows on two horizontal slices with z = -0.5dm and z=0 (dm: the maximum depth of scour) were also measured. The comparison about the flow on these horizontal slices is also carried out as shown in Fig. (12) and Fig. (13). At z = -0.5dm the scour hole in experiment is measured which starts from 2.4l and ends at -2.4l which is close to those in the simulation whose scour hole starts and ends at 2.2l and -2.2l respectively. In the spanwise direction, the scour size reaches to around 2.0 in both of the simulation and the experiment. At the height of z=0, the size of the scour hole is underestimated based on numerical simulation in the streamwise direction but agrees well in the spanwise direction.
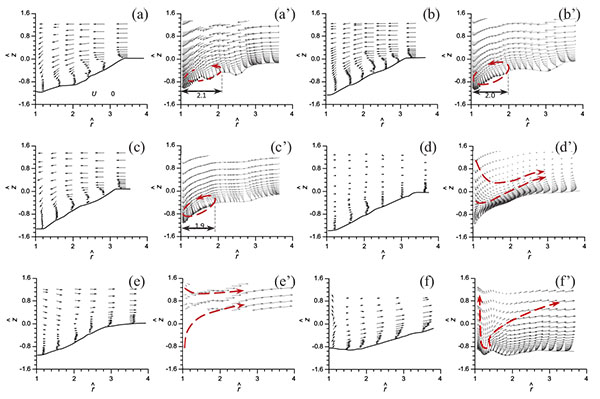
The profiles of local scour on the six vertical slices are also plotted with the vectors and contour of fluid speed superimposed as shown in Fig. (14) and Fig. (15) respectively. It is clear that the shape of the scour hole at each vertical slice in simulation is comparable with that in experiment. In general, the distributions of the speed give satisfactory agreement between simulation and experiment. There are some differences been the simulation and experiment, which may be due to the fact that when the scour develops, the mesh quality will become lower, especially near the bed, because the grid will be not normal to the bed and the angle decrease to a small value at the locations in which the terrain shows large gradient. This should be the most important reason of the errors in the numerical simulation, further validating the numerical method proposed in the present study.
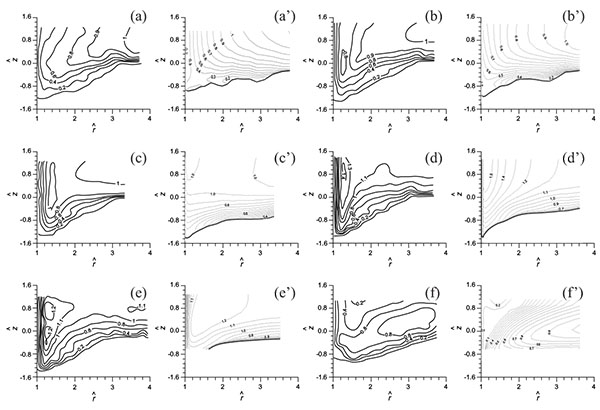
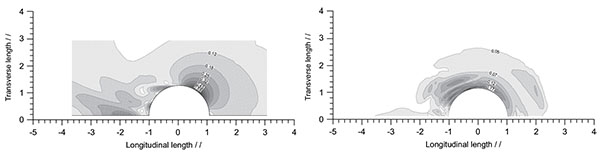
Fig. (16a and b) are the shear stress distribution on the channel bed before and after the formation of local scour. We can see that at the equilibrium stage the shear stress around the abutment decreases significantly and are lower than the critical shear stresses.
CONCLUSION
To conclude, in this study, a method combining the k-ε turbulence model with the sediment transportation model is applied and σ adaptive grid module is developed in commercial solver FLUENT to fit the variation of the channel bed. The formation of local scour is numerically simulated. This study aims at verifying the proposed numerical method. The shape of local scour at t=60min and the details of the flow fields after the formation of local scour is examined and compared with the experiment. We find that the proposed method successfully reproduces the development of local scour and the maximum depth of the scour hole which is the critical parameter in the design of the bridge is well predicted, indicating that the k-ε model together with the sediment transportation model is applicable to estimate the local scour for the bridge engineering. Apart from the validation purpose, we also found that the prediction for the abutment is much better than that for the pier. This is considered to be due to the fact that the strong horseshoe vortex is the main driven force for the scour in front of the pier but could not be well reproduced by URANS model. Further researches using LES turbulence model combined with more advanced sediment transportation model should be conducted.
NOTATION
The following symbols are used in this paper:
| CL | = lift coefficients for the particle; |
| CD | = drag coefficients for the particles; |
| d | = diameter of sediments. In this paper; |
| di | = diameter sediment whose weight is larger than i% of all sediment; |
| D* | = dimensionless particle parameter; |
| E | = roughness empirical constant; |
| g | = gravitational acceleration; |
| h | = elevation of the channel bed; |
| k | = turbulent kinematic energy; |
| kp | = turbulence kinetic energy at point “P”; |
| qbi | = bed load flux vector in the xi direction; |
| s | = relative density; |
| t | = time; |
| T | = non-dimensional excess bed shear stress; |
| Tm | = modified non-dimensional excess bed shear stress; |
| u* | = shear velocity; |
| ui | = instantaneous velocity component in xi direction; |
| ujp | = velocity of the movement of the computational mesh; |
| u'i | = velocity fluctuation in xi direction; |
| U | = mean approaching flow velocity; |
| Up | = velocity component parallel to the wall; |
| xi | = the coordinate along axis in Cartesian coordinate system; |
| α | = angle between the flow direction and the slope direction projected onto a horizontal plane; |
| γ | = sediments porosity; |
| Γwall | = dissipation constant; |
| δp | = distance from the center of control volume to the wall; |
| θ | = angle between the slope and horizontal plane; |
| θcr | = Shields number; |
| κ | = Karman constant; |
| ν | = kinematic viscosity; |
| νt | = turbulent viscosity; |
| ξ | = dimensionless density; |
| ρ | = density of clear water; |
| ρs | = sand density; |
| τ | = shear stress
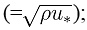 |
| |τ| | = magnitude of the bed shear stress; |
| τb,cr | = critical bed-shear stress at which sediment starts to move; |
| τ'b,cr | = critical bed-shear stress for sediments on horizontal bed; |
| τi | = bed shear stress in xi direction; |
| τij | = Reynolds stress; |
| φ | = angle of repose for sediments. |
ETHICS APPROVAL AND CONSENT TO PARTICIPATE
Not applicable.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.


