All published articles of this journal are available on ScienceDirect.
Vibration Safety Criteria for Surficial Rock Mass of Open Pit Slope Affected by Underground Mining Blasting Operations
Abstract
Introduction:
Blasting vibration velocity is an important index to evaluate the stability of mine slopes under blasting operations.
Objective:
In order to determine the blasting vibration safety criteria for slope rock mass scientifically and reasonably, the influence of stress waves on surficial rock mass of mine slopes was analyzed when stress waves propagate to the slope surface, and mathematical models for blasting vibration safety criteria are proposed based on the ultimate tensile stress criterion, the ultimate shear stress criterion and the Mohr-Coulomb criterion.
Results and Conclusion:
Combined with the field blasting operations during the open-pit to underground mining in Daye iron mine, the blasting vibration safety criteria is calculated. It is obtained that the blasting vibration safety criteria for the north slope and the south slope are 11.08cm/s and 10.20cm/s respectively. The results agree well with the Safety Regulations for Blasting in China and provide a reference to determine blasting vibration safety criteria for other similar projects.
1. INTRODUCTION
In open-pit to underground mines, partial collapse of surficial rock mass always occurs because the open-pit slopes are subjected to underground blasting mining operations [1], which trigger a serious threat to the workers and equipment. In order to ensure the safe production, it is the key technical problem to determine the blasting vibration safety criteria for slope rock mass scientifically and reasonably and to control blasting vibration effects.
The influence of blasting vibration on slope rock mass has been extensively studied. But most of these studies focused on the overall slope instability [2-5], and studies about the blasting-vibration-induced partial collapse of surficial slope rocks are rarely found. Kesimal et al. [6] studied the influence of blasting vibrations on slope instability at a limestone quarry by analyzing the blast-induced accelerations. Yang et al. [7] analyzed dynamic stability of open pit slope under blast loading based on time-history analysis and the software FLAC. Yan et al. [8] analyzed the variation of slope stability factors under blast loading by using the software GEO-SLOPE. The existing results show that numerical simulation is the main approach adopted to analyze the slope stability under blast loading [9-11]. Because of the complex action mechanism of blasts, the relevant theory study is relatively less.
In this paper, the surficial slope rock mass subjected blasting vibration in open-pit to underground mines is taken as research object. The mathematical models for blasting vibration safety criteria are proposed based on the ultimate tensile stress criterion, ultimate shear stress criterion and Mohr-Coulomb criterion. The value of blasting vibration safety criteria is calculated in case study and the results are proven to be reliable.
2. METHODS
2.1. Mathematical Models for Blasting Vibration Safety Criteria
When blasting stress waves propagate to the slope surface, the reflection-induced tensile stress will loose the surficial slope rock mass and result in some geological hazards, like partial collapse and rockfalls, which will threaten the whole projects [12]. Blasting stress waves can be divided into two categories according to the propagating paths: the stress waves propagating through the interior of media are known as body waves; the stress waves propagating across the surface are known as surface waves. Body waves can be divided into P-waves and S-waves.
According to the field conditions, blasting operations are always right below the toe of open-pit slopes. Blasting stress waves propagate through the interior of slopes to the surface and top of slopes. So only the influence of body waves (P-waves and S-waves) on the failure of slope rocks is studied.
Under blasting vibrations, particles within a certain range of the explosive source are disturbed and vibrations propagate from the explosive source in all directions. When blasting stress waves are incident at the free surface of slopes, reflection and refraction will be caused.
2.1.1. Reflection of P-waves at the Free Surface
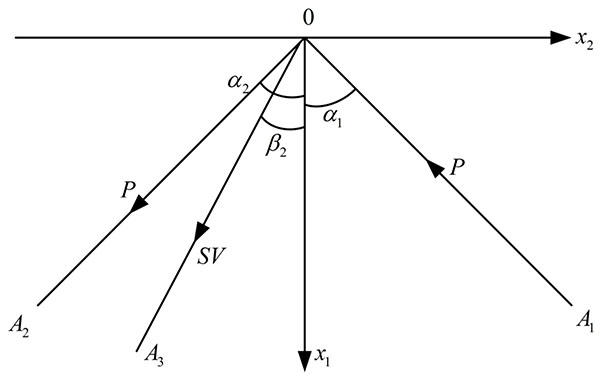
In stress wave theory, no transmission would be excited when a plane stress wave is incident on a free surface [13]. In this paper, we assumed that the blasting stress wave is a plane stress. In order to study the reflection of a blasting stress wave on a free surface, a coordinate system Ox1x2 is set up, and the plane x1 = 0 is defined to be the free surface. The slope rock mass is located in the x1 > 0 region, and the x1 < 0 region represents the air. Suppose a blasting stress wave is a plane harmonic P-wave, and α1 is defined as the incident angle, 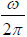 as the frequency, as shown in Fig. (1). The displacement Φ1 orthogonal to the wave front is given as follows:
as the frequency, as shown in Fig. (1). The displacement Φ1 orthogonal to the wave front is given as follows:
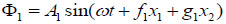 |
(1) |
where A1 is wave amplitude, 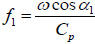 ,
, 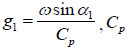 is the wave speed of P-waves.
is the wave speed of P-waves.
u1 and v1 are the displacements in the directions of x1 and x2, given by:
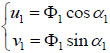 |
(2) |
Let α2 be the reflection angle of the reflected P-wave, its displacement orthogonal to the wave front is given by:
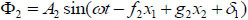 |
(3) |
where A2 is wave amplitude, 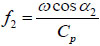 ,
, 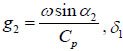 is a constant and means the phase change. u2 and v2 are given by:
is a constant and means the phase change. u2 and v2 are given by:
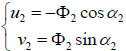 |
(4) |
At the free surface (x1 = 0), the normal stress σ11 and the tangential stress σ12 both are zero. Let u and v be the total displacement made up from the incident and reflected P-waves. According to the Hooke’s law, the components of stress tensor are obtained as:
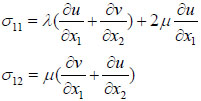 |
(5) |
where λ and μ are the Lame constants.
Substituting from (1) and (3), equation (5) becomes:
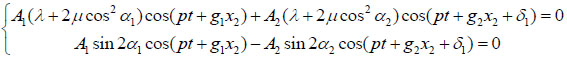 |
(6) |
For all (x2, t), the two parts of equation (5) cannot be satisfied simultaneously. If the first part is satisfied, g1 = g2, δ1 = 0 and A1=−A2. But the latter part cannot be satisfied. So there must be a reflected S-wave other than a reflected a P-wave to make the both parts of equation (5) satisfied.
Let β2 be the reflection angle of the reflected S-wave, its displacement orthogonal to the wave front is given by:
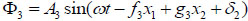 |
(7) |
where Cs is the wave speed of S-waves, A3 is wave amplitude, 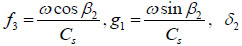 is a constant for phase change. Because the oscillations of an S-wave occur perpendicular to the direction of energy transfer and it is supposed that the movement only occurs in the same plane, the oscillations lie in the Ox1x2 plane, known as a SV-wave. Its displacements are given by:
is a constant for phase change. Because the oscillations of an S-wave occur perpendicular to the direction of energy transfer and it is supposed that the movement only occurs in the same plane, the oscillations lie in the Ox1x2 plane, known as a SV-wave. Its displacements are given by:
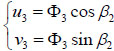 |
(8) |
Let u = u1 + u2 + u3 and v = v1 + v2 + v3, the boundary condition of σ12 = 0 on x1 = 0 can be written as:
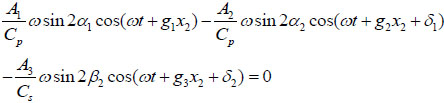 |
(9) |
If equation (3) is satisfied for all (x2, t), there must be g1 = g2 = g3, as follows:
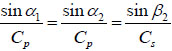 |
(10) |
So,
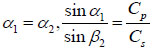 |
(11) |
The reflection angle of reflected P-wave equals to the incident angle and the ratio of the sine of the reflection angle of reflected S-wave to the sine of the incident angle equals to the ratio of the S-wave’s speed to the P-wave’s speed. Because Cp > Cs, the reflection angle β2 greater than the incident angle α1. The values of δ1 and δ2 can only be zero or π. Now let δ1 = δ2 = 0, the amplitudes satisfy:
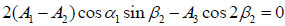 |
(12) |
Similarly, let g1 = g2 = g3 and δ1 = δ2 = 0 in the boundary condition of σ11 = 0 at x1 = 0. Then the amplitudes satisfy:
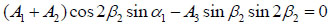 |
(13) |
Equations (12) and (13) form a linear system of equations. For a given incident P-wave, the amplitudes of reflected waves A2 and A3 can be obtained as follows,
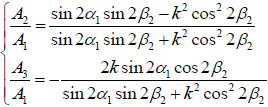 |
(14) |
where 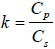 .
.
For normal incidence, it can be obtained that A3 = 0 and A1 = A2 from equations (12) and (13). In this case, the incident P-wave is reflected as a P-wave. The amplitude of the reflected P-wave is the same with the incident P-wave and its phase changes π. The incident compressive wave becomes a tensile wave.
2.1.2. Reflection of S-waves at the Free Surface
Assume a S-wave incident on the free surface with an incident angle of 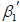 , which propagates in the Ox1x2 plane. Different from P-waves, the polarization of S-wave must be specified. Because an arbitrary displacement can be polarized to two components perpendicular to each other, the S-wave is polarized parallel to the Ox1x2 plane known as SV-wave and perpendicular to the Ox1x2 plane known as SH-wave.
, which propagates in the Ox1x2 plane. Different from P-waves, the polarization of S-wave must be specified. Because an arbitrary displacement can be polarized to two components perpendicular to each other, the S-wave is polarized parallel to the Ox1x2 plane known as SV-wave and perpendicular to the Ox1x2 plane known as SH-wave.
For a SV-wave, the displacements u3 = 0 and u1 and u2 refer to x1, x2 and t. So the problem is a plane motion problem. The solution method is similar as the case of the incident P-wave. The incident angle of SV-wave is 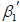 , and the boundary conditions at x1 = 0 are σ11 = 0 and σ12 = 0, as shown in Fig. (2).
, and the boundary conditions at x1 = 0 are σ11 = 0 and σ12 = 0, as shown in Fig. (2).
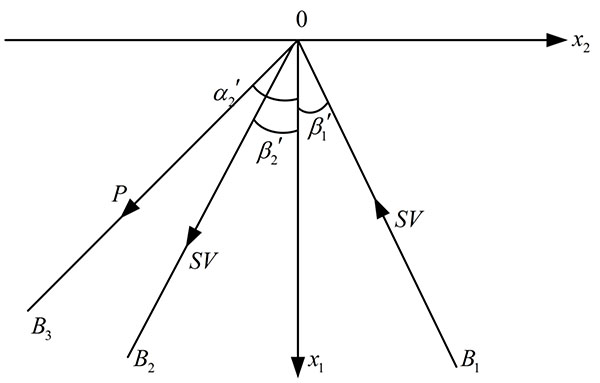
The boundary conditions can be satisfied only when both reflected P-waves and SV-waves are excited. The reflection angle of reflected SV-wave equals to the incident angle, i.e. 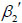 =
= 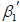 . The reflection angle of reflected P-wave is obtained from the equation
. The reflection angle of reflected P-wave is obtained from the equation 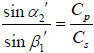 . Obviously
. Obviously  . The amplitude of incident SV-wave is B1, the amplitude of reflected SV-wave is B2 and the amplitude of reflected P-wave is B3.
. The amplitude of incident SV-wave is B1, the amplitude of reflected SV-wave is B2 and the amplitude of reflected P-wave is B3.
Then the boundary conditions at x1= 0 can be written as follows,
 |
(15) |
For a given incident SV-wave, the amplitudes of reflected waves B2 and B3 can be obtained as follows,
 |
(16) |
For SH-waves, whose propagating direction is perpendicular to the Ox1x2 plane, no movement is caused in x1 and x2 directions, i.e. u1 = 0 and u2 = 0. When a SH-wave is incident on the free surface, it can be found form boundary conditions that only a reflected SH-wave is produced. The reflection angle equals to the incident angle. The reflected SH-wave has the same amplitude and the opposite phase with the incident SH-wave.
2.1.3. Mathematical Models for Blasting Vibration Safety Criteria
Based on stress wave theory, wave speed is closely related to the density, elastic modulus and Poisson’s ratio [14], the wave speeds of P-waves and SV-waves are given by:
 |
(17) |
where Cp is the wave speed of P-waves, Cs is the wave speed of S-waves, Ed is the dynamic modulus, ρ is density, ν is the Poisson’s ratio.
By analyzing the propagation of blasting stress wave in rock mass and the stress state of rock mass under blasting impacts, the formulas of dynamic stress at wave fronts are given by [15]:
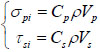 |
(18) |
where σpi is the normal stress induced by the incident P-wave, τsi is the shear stress induced by the incident S-wave, Vp is the vibration velocity induced by the incident P-wave, Vs is the vibration velocity induced by the incident S-wave.
According to the ultimate tensile stress criterion, if the incident angle of stress waves (P-waves, S-waves) is θ, then:
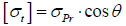 |
(19) |
where [σt] is the ultimate tensile strength, σPr is the tensile stress induced by reflected P-waves.
If a P-wave reflects on the free surface, θ = α1 according to the definition of incident angle in Chapter 2.1. By substituting equations (14), (17) and (18) to equation (19), the blasting vibration safety criteria of P-waves is given by:
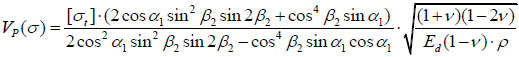 |
(20) |
If a S-wave reflects on the free surface, θ = 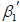 according to the definition of incident angle in Chapter 2.2. By substituting equations (16), (17) and (18) to equation (19), the blasting vibration safety criteria of P-waves is given by:
according to the definition of incident angle in Chapter 2.2. By substituting equations (16), (17) and (18) to equation (19), the blasting vibration safety criteria of P-waves is given by:
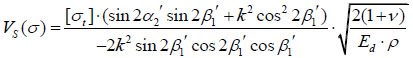 |
(21) |
2.2. Ultimate Strength of Slope Surficial Rocks
Numerous studies and engineering practices prove that the failure characteristics of rock mass under static and dynamic loads are of a huge difference. Different rocks and different stress states result in different failure modes, but the main failure mode can be found. For hard brittle rocks (such as marble and diorite), shear failure or tensile failure dominates the failure modes, and the envelope is approximate a straight line [16]. But under blasting-vibration-induced dynamic loads, shear failure is rarely found in such rock materials, and tensile failure.
The strength of rock mass under blasting-vibration-induced dynamic loads will increase to some certain extent, the increasing of ultimate tensile strength and elastic modulus is dependent to loading rate. The relation between static tensile strength and dynamic tensile strength is given by [17]:
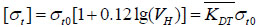 |
(22) |
where [σt]—dynamic tensile strength;
σt0—static tensile strength;
VH—loading rate, VH = σH /σ1;
σH—arbitrary loading speed(σH ≥1);
σ1—loading speed, σ1=0.1Mpa/s;
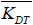 —increasing factor for tensile strength.
—increasing factor for tensile strength.
Similarly, the relation between static elastic modulus and dynamic elastic modulus is given by [18]:
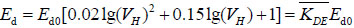 |
(23) |
where Ed—dynamic elastic modulus;
Ed0—static elastic modulus;
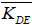 —increasing factor for elastic modulus.
—increasing factor for elastic modulus.
The loading speed of blasting seismic waves is up to 106MPa/s and in general, the sensitive loading speed of slopes and underground structures is 10~103 MPa/s [17]. So, when the σH is 10~103 MPa/s, it can be calculated that from equations (22) and (23):
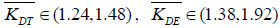 |
(24) |
The average values of the increasing factor for tensile strength and the increasing factor for elastic modulus are 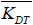 = 1.36,
= 1.36, 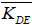 = 1.65 respectively.
= 1.65 respectively.
3. RESULTS AND DISCUSSIONS
3.1. Field Conditions of Open-pit to Underground Mining in Daye Iron Mine
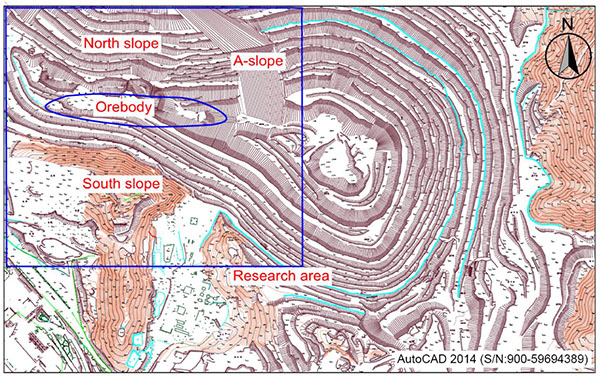
Daye Iron Mine is located in Tieshan District, Huangshi City, Hubei Province, PR China, about 90km west to Wuhan City, 25km east to the downtown of Huangshi City, 15km southeast to Daye City, as shown in Fig. (3). A deep open pit has been formed throughout 100 years of mining activities, which is 2400m E-W and 1000m N-S. The east open pit of Daye Iron Mine was selected as the study area, as shown in Fig. (4). The north slope is 170m-270m above mean sea level (ASL), and the south slope is 86m-200m ASL. The overall slope angle varies from 38o to 43o, and some inter-ramp angles are up to 53o. It is a precursory and typical open-pit to underground mine in China. Marble mainly distributes in the south slope and diorite mainly distributes in the north slope. In open-pit mining, the bench height is 12m and the bottom elevation is -48m ASL. In order to ensure the slope stability, the bottom has backfilled up to ±0 m ASL. In underground mining, sublevel caving method is adopted. The current mining operations are at -84m ASL, and the occurrence of ores is deep to -168m ASL.
The static mechanical parameters of the rock mass in open-pit slopes of Daye Iron Mine are obtained by compression tests and tensile strength tests. The rock samples were processed into cylinder with diameter of 50mm and height of 100mm, and part of samples are showing in Fig. (5), and compression tests of rock sample are showing in Fig. (6). The details of laboratory tests of mechanical parameters of the rock samples are described in Zhang’s research [19]. With equation (24) taken into consideration, the dynamic mechanical parameters are calculated, as listed in Table 1.

| Parameters | Symbol | Units | Marble | Diorite |
|---|---|---|---|---|
| Static elastic modulus | Ed0 | GPa | 16.22 | 18.37 |
| Static tensile strength | σt0 | GPa | 12.11 | 13.82 |
| Dynamic elastic modulus | Ed | GPa | 26.76 | 30.31 |
| Dynamic tensile strength | σt | GPa | 16.47 | 18.80 |
| Density | ρ | kg/m3 | 2710 | 2830 |
| Poisson’s ratio | v | / | 0.23 | 0.23 |

3.2. Theoretical Analysis of Blasting Vibration Safety Criteria
According to the field conditions, a section along the center of underground stope is selected and simplified to determine the range of incident angles when blasting stress waves propagate to slope surfaces, as shown in Fig. (7). Benches on south and north slopes are neglected. The overall slope angle of the north slope is 45° and the slope height is 245m; the overall slope angle of the south slope is 39° and the slope height is 128m. The current mining operations are at -84m ASL, and the occurrence of ores is deep to -168m ASL.
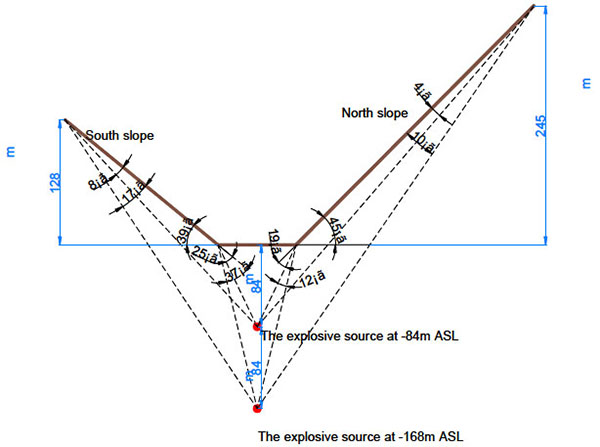
It can be obtained from Fig. (7) that for north slopes, the range of incident angle is from 71° to 86° and for south slopes, the range of incident angle is from 51° to 82°.
In order to ensure the stability of mine slopes, the influence of underground mining blasting operations should be modified according to its importance and potential damage. Because the mine slopes in Daye iron mine are permanent, it will seriously threaten the workers and underground stopes once rockfalls, collapses and even landslides occur. So the modification factor of 1.7 is chosen according to the Specifications of Earthquake Resistant Design for Highway Engineering in China [20].
According to the parameters listed in Table 1, the blasting vibration safety criteria can be calculated from equations (20) and (21), as follows:
 |
(25) |
According to the relevant research achievements, the frequency of incident stress waves has little influence on rock strength [21]. According to equation (25), in order to ensure the safety of the slope is absolute, the blasting vibration safety criteria for north slope and south slope can be proposed to 11.08cm/s and 10.20cm/s respectively.
According to the Safety Regulations for Blasting in China [22], the blasting vibration safety criteria for permanent rock slopes is 5cm/s to 15cm/s. The rock-strength-based blasting vibration safety criteria in this paper agree well with it, but are more accurate and rational. The criteria proposed in this paper will play a significant role in underground mining blasting operations and preventing from rockfalls.
CONCLUSION
- The influence of stress wave on surficial rock mass was analyzed when stress waves travel to the slope surface, and a mathematical model for blasting vibration safety criteria is proposed based on the ultimate tensile stress criterion, ultimate shear stress criterion and Mohr-Coulomb criterion.
- In order to ensure the stability of mine slopes, the influence of underground mining blasting operations should be modified according to its importance and potential damage.
- According to the field conditions, the blasting vibration safety criteria for the north slope and south slope in Daye iron mine are 11.08cm/s and 10.20cm/s respectively, which accords with the Safety Regulations for Blasting in China, and is more accurate and rational. The results provide a scientific reference for the relevant specifications.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
The study was sponsored by the National Natural Science Foundation of China (Grant No.41372312 and No.51379194), the Fundamental Research Funds for the Central Universities of China University of Geosciences (Wuhan) (Grant No. CUGL140817), the Natural Science Foundation of Hubei Province of China (Grant No. 2014CFB894) and the China Postdoctoral Science Foundation (Grant No. 2014M552113).


