All published articles of this journal are available on ScienceDirect.
Dynamic Response of RC Frame Structures Under the Action of Mining Blasting
Abstract
Introduction:
In this study, the acceleration time-history curve of blasting vibration is obtained at different explosion distances in different amount of explosion with MATLAB analysis software to determine the dynamic response of mining blasting vibration to surrounding reinforced concrete (RC) frame structures.
Objective:
Moreover, this paper discusses the dynamic response of two RC structures with different numbers of stories that happen to blasting vibration waves generated by using different amount of explosion at different blasting distances.
Result:
Results show that the vibration response of the RC frame structures may be larger under the action of blasting vibration. The smaller the explosion source distance, the lower is the structure, and the larger is the story drift, that is, in general, with the same explosion charge and small explosion source, the deformation of lower structure is larger than the higher. The larger the explosion source distance, the smaller is the change range of floor displacement. A larger distance results in a weaker blasting vibration response.
Conclusion:
Furthermore, the acceleration amplitudes of the top stories are almost equal in both structures with the same amount of explosion and the same explosion distance. It is suggested that the higher the structure , the greater is the influence of explosion source distance on the change rate of floor displacement and story drift . Therefore, allowable safety distance should be determined according to the mining conditions and structural height during structure design.
1. INTRODUCTION
Blasting technology plays an increasingly important role in the process of mining. Blasting vibration and damage on adjacent buildings are common, and damage to buildings by mining blasting is affected by several factors. These factors include the characteristics of the blasting wave, the composition of the structure, construction quality, and the characteristics of foundation soil on site. The generation of a blasting wave involves a process of random vibration. Therefore, the destruction of accurately estimated buildings by blasting waves is a complicated problem. Guaranteeing the safety of buildings around a mining area is thus an urgent problem.
Existing studies have examined the dynamic collapse and dynamic response of a frame structure under seismic action. For example, Liu et al. [1] adopted time–history response analysis method and described the transition from static to vibration and then to collapse. These researchers also presented measures for improving the seismic performance of a frame structure. Liu et al. [2] analyzed three main bearing capacity reduction processes of a 10-layer frame structure, namely, elastic work, cracking, and collapse. These researchers actualized the entire process of damaging building frame structures and identified key points in structures under a severe earthquake. Liu and Chen also recommended measures for improving the seismic performance of a frame structure. Huang et al. [3] discussed the process of collecting waveform data from artificial blasting events and extracting relatively regular waveform characteristics from a natural seismic wave. The differences between blasting and natural seismic waves were identified and explored in detail. Jiang et al. [4] analyzed seismic fragility assessment of RC moment-resisting frames designed according to the current Chinese seismic design code. Yang and Gao [5] determined the out-of-plane collapse process of a filler wall under rare earthquake action through numerical simulation. These researchers confirmed that a frame filler wall falls off easily when no construction measures are undertaken; the wall then collapses under rare earthquake action. Zhang and Huang [6] studied the vibration response of a particle to rock and soil mass during an explosion by establishing a mine blasting model in the context of mining engineering. Kim and Kang [7] analyzed super tall mega frame buildings by using a multi-level condensation method. A research group (Cheng and Su [8]; Cheng and Wang [9],) also elaborated on the failure mechanism and dynamic response of a lining structure and soil mass structure surrounding a tunnel with a curved wall. Jiang et al. [10] analyzed damage-control seismic design of moment-resisting RC frame buildings. Ko et al. [11] evaluated seismic behavior of RC moment resisting frame with masonry infill walls. Research group [12] used MATLAB to examine the dynamic response of concrete frame structure under a blasting demolition environment, suggesting that moderate explosive energy should be used in demolition engineering to decrease the influence on surrounding buildings. Zhou et al. [13] conducted the test on peak acceleration amplification of soil layer in artificial blast wave. Wang et al. [14] studied the dynamic response of the frame construction building to the open-pit blasting seismic waves. The result shows that frequent blasting vibration causes the stress concentration between the wall and the beam. It is necessary to completely take into account the dynamic response difference between the frame construction building and the masonry filler wall so as to reduce the frequency of blast induced vibration to the minimum extent. Coffield and Adeli [15] studied the irregular steel building structures subjected to blast loading.
Domestic and foreign scholars have extensively studied the blasting parameters in mining areas and the influence of blasting on surrounding buildings. Lu et al. [16] examined internal force redistribution in a steel–concrete structure, as well as the relative defense mechanism caused by vehicle collision and the failure load-bearing columns during an explosion. Hao and Wu [17] studied the dynamic response of an RC frame structure to underground motion caused by an underground explosion, they eventually established a discrete model. By conducting an actual survey on an open gold mine in Cangshang and by analyzing slope stability, blasting vibration strength, and uneven surface settlement, Zhan et al. [18] determined that the main reason for civil house cracking is the significant difference in the compressibilities of foundation soil. An uneven surface settlement results in house cracking. Shi et al. [19] analyzed the influence of vibrations from open-pit mining blasting on neighboring buildings and compared the degree of influence of various factors using grey relation method in combination with engineering practice. Wu et al. [20] studied a blasting vibration appraisal method and calculated the safe distance based on the degree of influence of excavation blasting on adjacent buildings in the Shuibuya Quarry. Tan et al. [21] measured the vibration of a three-layer frame structure that lies on the slope of an open-pit mine boundary near the slope shoulder as a result of construction site blasting. Chen et al. [22] studied the building dynamic response under explosion load. Hao et al. [23] studied the reliability of RC column and frame with FRP strengthening subjected to explosive load. And the effectiveness of FRP strengthening of the RC column on their blast load-carrying capacities was demonstrated. These researchers established a damage accumulation model of the reinforced concrete (RC) member and in the overall structure under the action of frequent blasting vibration. The results showed that the damage is greater than the structural integrity, and that the weakest parts of the frame structure under frequent blasting vibration are located at the top floor and on top of the side column positioned at the bottom of the structure. Yan et al. [24] assessed the seismic impact on residences during blasting excavation of a large-scale rock slope in China. These researchers also discussed the response caused by ground motion at different frequencies, damage characteristics, the spatial variations in ground motion, and the soil consolidation interactions during the structural response.
Although international scholars have investigated numerous studies on blasting vibration, their studies mainly focused on the influencing factors that influence building damage, impact scope evaluation, and the dynamic response of the rock mass itself. In sum, most scholars have analyzed the dynamic response of an RC frame structure to explosions, but studies are limited to the explosive action of the building itself. Moreover, existing works do not consider the influence of explosions on the surrounding buildings. Therefore, the present study focuses on the dynamic response of a surrounding frame structure under the action of a blasting vibration wave caused by mining, and in order to compare and analyze, the frame structures that with different floor number were selected. The findings of this research could serve as a reference for the construction of buildings around the mining area.
2. ANALYSIS MODEL AND BLASTING SEISMIC WAVE
2.1. Engineering Overview
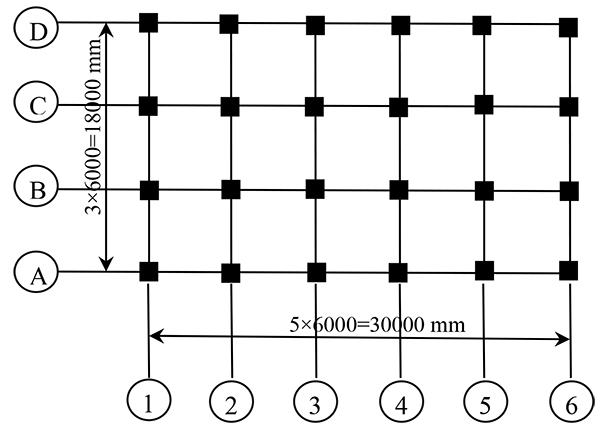
In order to study the dynamic response of surrounding frame structure under blasting vibration, residential buildings that with 7 and 16 stories were examined. These buildings belonged to RC frame structures. Moreover, these constructions share the same structure form and are similar in terms of other parameters. The building parameters were as follows: North–South total width was 18 m, East–West total length was 30m, column spacing was 6 m, the story height of the first floor was 3.9m, and the story heights of the remaining stories were 3.0m. Concrete strength was 30 MPa, elastic modulus E was 30 GPa, and Poisson’s ratio was 0.2. The thickness of floor slab was 120 mm, the column section was 600mm × 600mm, and the beam section was 550 mm × 300mm. The dead load of the floor slab was 2.50 kN/m2 (not including self-weight), the live load of the floor slab was 2.00 kN/m2, and the live load of the roof was 0.5 kN/m2. Earthquake intensity was VIII, and the design earthquake group belonged to the second group. The site classification was class II. The standard floor layout of the building is shown in Fig. (1).
2.2. Blasting Seismic Wave
MATLAB software was utilized to simulate a blasting seismic wave and when considering the loading model of space explosion; the site condition indirectly through the amplitude envelope function was considered. According to the existing literature (Guo et al. [25]), the amplitude envelope function is expressed as Eq. (1), and the power spectrum function is written as Eq. (2).
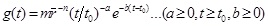 |
(1) |
where
 is the explosion distance ratio (
is the explosion distance ratio (
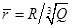 ); Q is the current amount of explosive charge; R is the explosive distance; m, n, a, and b are undetermined constants; t is the time; and t 0 is the delay time.
); Q is the current amount of explosive charge; R is the explosive distance; m, n, a, and b are undetermined constants; t is the time; and t 0 is the delay time.
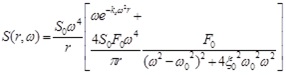 |
(2) |
where S 0, ks, and F 0 are all constants (determined through the experiment); r is the distance of the blast center; ω 0 is the characteristic frequency (ω0>0); and ξ 0 is the damping coefficient.
Fourier amplitude spectrum A (r, ω) can be calculated by power spectrum S (r, ω):
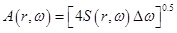 |
(3) |
Where Δω=2π× sampling frequency/FFT length, and Δω is the frequency interval.
Converting Fourier amplitude spectrum A(r, ω) and random phase spectrum ϕ(ω) to real and imaginary parts of Fourier transform, then conducting inverse Fourier transform, approximate acceleration time history a(t) of artificial seismic wave can be obtained:
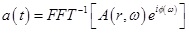 |
(4) |
Where ϕ(ω) is phase spectrum, it is a random number between 0 and π; i is imaginary.
The final equation of artificial seismic wave can be expressed as:
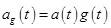 |
(5) |
According to existing literature (Lin [26]; Huang [27], m=448.53, n=2.03, C=665.4, ω0=100, a=60, b=80, S0=7.5×10-8, ks=4.35×10-5, and F0=9.1×10-6.
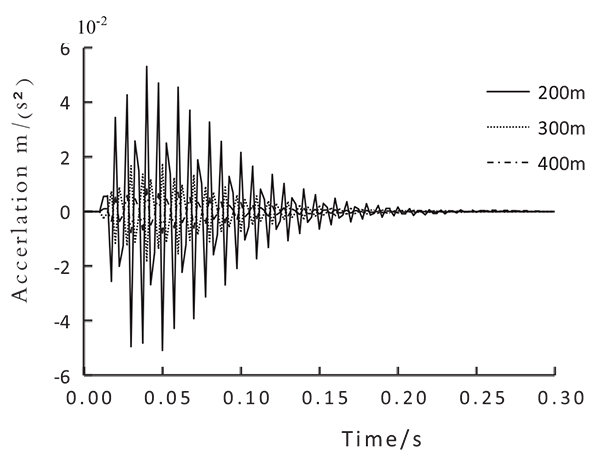
The explosion wave has a considerable relation to the explosion amount and the explosion distance. The time-history curves of blasting seismic acceleration are constructed at the specified distances of 200, 300, and 400 m in the explosion amounts 200, 300, and 400 kg, as shown in Fig. (2).
3. MASS PARTICIPATION RATIO AND DEFORMATION DIAGRAM
The dynamic responses of the 7-story and 16-story frame structures located at a mining field were analyzed using SAP2000 at distances of 200, 300, and 400 m.
The period and mass participation ratio of the first three vibration modes are presented in Tables 1 and 2. UX, UY, and UZ are the mass participation ratios in the X, Y, and Z directions, respectively. Sum UX, Sum UY, and Sum UZ are the accumulation values of the mass participation ratio in the X, Y, and Z directions, respectively. RX, RY, and RZ are the mass participation ratios circling the X, Y, and Z axes, respectively. The deformations of the structures under different modes are highlighted in Tables 3 and 4.
| Distance | Order | Period | UX | UY | UZ | Sum UX |
Sum UY |
Sum UZ |
RX | RY | RZ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 200m | 1 | 0.57 | 0.80 | 0.00 | 0.00 | 0.80 | 0.00 | 0.00 | 0.00 | 0.67 | 0.46 |
| 2 | 0.53 | 0.00 | 0.80 | 0.00 | 0.80 | 0.80 | 0.00 | 0.34 | 0.00 | 0.12 | |
| 3 | 0.18 | 0.10 | 0.00 | 0.00 | 0.90 | 0.80 | 0.00 | 0.00 | 0.00 | 0.06 | |
| 300m | 1 | 0.57 | 0.80 | 0.00 | 0.00 | 0.80 | 0.00 | 0.00 | 0.00 | 0.67 | 0.46 |
| 2 | 0.53 | 0.00 | 0.80 | 0.00 | 0.80 | 0.80 | 0.00 | 0.34 | 0.00 | 0.12 | |
| 3 | 0.18 | 0.10 | 0.00 | 0.00 | 0.90 | 0.80 | 0.00 | 0.00 | 0.00 | 0.06 | |
| 400m | 1 | 0.57 | 0.80 | 0.00 | 0.00 | 0.80 | 0.00 | 0.00 | 0.00 | 0.67 | 0.46 |
| 2 | 0.53 | 0.00 | 0.80 | 0.00 | 0.80 | 0.80 | 0.00 | 0.34 | 0.00 | 0.12 | |
| 3 | 0.18 | 0.10 | 0.00 | 0.00 | 0.90 | 0.80 | 0.00 | 0.00 | 0.00 | 0.06 |

| Distance | Order | Period | UX | UY | UZ | Sum UX |
Sum UY |
Sum UZ |
RX | RY | RZ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 200m | 1 | 1.37 | 0.79 | 0.00 | 0.00 | 0.79 | 0.00 | 0.00 | 0.00 | 0.90 | 0.46 |
| 2 | 1.26 | 0.00 | 0.80 | 0.00 | 0.79 | 0.80 | 0.00 | 0.71 | 0.00 | 0.12 | |
| 3 | 0.45 | 0.10 | 0.00 | 0.00 | 0.89 | 0.80 | 0.00 | 0.00 | 0.00 | 0.06 | |
| 300m | 1 | 1.37 | 0.79 | 0.00 | 0.00 | 0.79 | 0.00 | 0.00 | 0.00 | 0.90 | 0.46 |
| 2 | 1.26 | 0.00 | 0.80 | 0.00 | 0.79 | 0.80 | 0.00 | 0.71 | 0.00 | 0.12 | |
| 3 | 0.45 | 0.10 | 0.00 | 0.00 | 0.89 | 0.80 | 0.00 | 0.00 | 0.00 | 0.06 | |
| 400m | 1 | 1.37 | 0.79 | 0.00 | 0.00 | 0.79 | 0.00 | 0.00 | 0.00 | 0.90 | 0.46 |
| 2 | 1.26 | 0.00 | 0.80 | 0.00 | 0.79 | 0.80 | 0.00 | 0.71 | 0.00 | 0.12 | |
| 3 | 0.45 | 0.10 | 0.00 | 0.00 | 0.89 | 0.80 | 0.00 | 0.00 | 0.00 | 0.06 |
| Vibration modes | Distance | ||
|---|---|---|---|
| 200m | 300m | 400m | |
| 1st mode |  |
 |
 |
| 2nd mode |  |
 |
 |
| 3rd mode |  |
 |
 |
| Vibration mode | Distance | ||
|---|---|---|---|
| 200m | 300m | 400m | |
| 1st mode |  |
 |
 |
| 2nd mode |  |
 |
 |
| 3rd mode |  |
 |
 |
As can be seen from Table 1, the three mode periods of the 7-story frame structure are 0.53s, 0.57s and 0.18s, respectively. First of all, for the first mode, UX is 0.8, UY is 0, UZ is 0, Rx is 0, RY is 0.67 and RZ is 0.46, indicating that the structure is translational along the X axis and torsional around the Y axis and Z axis. Similarly, we can determine the second mode is translational along the Y axis and torsional around the X axis and Z axis, and the third mode is translational along the Z axis and torsional around the X axis and Y axis.
As can be seen from Table 2, the three mode periods of 16-story frame structure are 1.26s, 0.45s and 1.37s, respectively. First of all, for the first mode, the structure is translational along the X axis and torsional around the Y axis and Z axis, the second mode is translational along the Y axis and torsional around the X axis and Z axis, and the third mode is translational along the Z axis and torsional around the X axis and Y axis
As can be seen from Tables 3 and 4, the deformation of 7-story frame structure is significantly greater than that of 16-story frame structure under the same blast wave. Both the 7-storey and 16-story frame structures, blasting distance is closer, the overall deformation of structure is larger. On the contrary, blasting distance is farther, the overall structure deformation is smaller.
4. DYNAMIC RESPONSES
4.1. Displacement
Tables 5 to 10 list the floor displacements and story drifts of the 7-story and 16-story frame structures under the action of different amount of explosion per blasting field, respectively, their distances from the explosion source are 200 m, 300 m and 400 m., their amount of explosive are 200 kg, 300 kg and 400 kg, respectively.
| Floors | 200 m | 300 m | 400 m | |||
|---|---|---|---|---|---|---|
| Floor displacement (m) |
Story drift (m) |
Floor displacement (m) |
Story drift (m) |
Floor displacement (m) |
Story drift (m) |
|
| 1 | 1.021E-02 | 1.021E-02 | 9.188E-04 | 9.188E-04 | 8.534E-04 | 8.534E-04 |
| 2 | 1.863E-02 | 8.420E-03 | 1.670E-03 | 7.512E-04 | 1.557E-03 | 7.036E-04 |
| 3 | 2.514E-02 | 6.510E-03 | 2.258E-03 | 5.880E-04 | 2.101E-03 | 5.440E-04 |
| 4 | 3.046E-02 | 5.320E-03 | 2.735E-03 | 4.770E-04 | 2.545E-03 | 4.440E-04 |
| 5 | 3.850E-02 | 8.040E-03 | 3.458E-03 | 7.230E-04 | 3.217E-03 | 6.720E-04 |
| 6 | 4.360E-02 | 5.100E-03 | 3.910E-03 | 4.520E-04 | 3.643E-03 | 4.260E-04 |
| 7 | 4.559E-02 | 1.990E-03 | 4.088E-03 | 1.780E-04 | 3.809E-03 | 1.660E-04 |
| Floor | 200 m | 300 m | 400 m | |||
|---|---|---|---|---|---|---|
| Floor displacement (m) |
Story drift (m) |
Floor displacement (m) |
Story drift (m) |
Floor displacement (m) |
Story drift (m) |
|
| 1 | 5.641E-03 | 5.641E-03 | 2.490E-03 | 2.490E-03 | 3.858E-03 | 3.858E-03 |
| 2 | 1.133E-02 | 6.490E-03 | 4.989E-03 | 2.881E-03 | 4.081E-03 | 2.230E-04 |
| 3 | 1.782E-02 | 6.530E-03 | 7.870E-03 | 2.890E-03 | 4.323E-03 | 2.420E-04 |
| 4 | 2.435E-02 | 5.680E-03 | 1.076E-02 | 2.890E-03 | 5.661E-03 | 1.338E-03 |
| 5 | 3.003E-02 | 4.900E-03 | 1.328E-02 | 2.520E-03 | 5.703E-03 | 4.200E-05 |
| 6 | 3.493E-02 | 4.830E-03 | 1.542E-02 | 2.140E-03 | 6.314E-03 | 6.110E-04 |
| 7 | 3.976E-02 | 4.990E-03 | 1.753E-02 | 2.110E-03 | 6.476E-03 | 1.620E-04 |
| 8 | 4.475E-02 | 1.500E-04 | 1.974E-02 | 2.210E-03 | 6.583E-03 | 1.070E-04 |
| 9 | 4.490E-02 | 3.580E-03 | 2.134E-02 | 1.600E-03 | 6.906E-03 | 3.230E-04 |
| 10 | 4.848E-02 | 1.820E-03 | 2.187E-02 | 5.300E-04 | 7.315E-03 | 4.090E-04 |
| 11 | 5.030E-02 | 1.930E-03 | 2.216E-02 | 2.900E-04 | 7.380E-03 | 6.500E-05 |
| 12 | 5.223E-02 | 1.630E-03 | 2.301E-02 | 8.500E-04 | 7.394E-03 | 1.400E-05 |
| 13 | 5.386E-02 | 1.340E-03 | 2.363E-02 | 6.200E-04 | 7.626E-03 | 2.320E-04 |
| 14 | 5.520E-02 | 1.600E-04 | 2.374E-02 | 1.100E-04 | 7.792E-03 | 1.660E-04 |
| 15 | 5.536E-02 | 6.200E-04 | 2.434E-02 | 6.000E-04 | 7.950E-03 | 1.580E-04 |
| 16 | 5.598E-02 | 4.848E-03 | 2.468E-02 | 3.400E-04 | 8.109E-03 | 1.590E-04 |
| Floors | 200 m | 300 m | 400 m | |||
|---|---|---|---|---|---|---|
| Floor displacement (m) |
Story drift (m) |
Floor displacement (m) |
Story drift (m) |
Floor displacement (m) |
Story drift (m) |
|
| 1 | 1.142E-02 | 1.142E-02 | 9.711E-03 | 9.711E-03 | 8.852E-04 | 8.852E-04 |
| 2 | 2.082E-02 | 9.400E-03 | 1.771E-02 | 7.999E-03 | 1.615E-03 | 7.298E-04 |
| 3 | 2.811E-02 | 7.290E-03 | 2.391E-02 | 6.200E-03 | 2.179E-03 | 5.640E-04 |
| 4 | 3.404E-02 | 5.930E-03 | 2.896E-02 | 5.050E-03 | 2.640E-03 | 4.610E-04 |
| 5 | 4.303E-02 | 8.990E-03 | 3.661E-02 | 7.650E-03 | 3.337E-03 | 6.970E-04 |
| 6 | 4.873E-02 | 5.700E-03 | 4.145E-02 | 4.840E-03 | 3.779E-03 | 4.420E-04 |
| 7 | 5.095E-02 | 2.220E-03 | 4.334E-02 | 1.890E-03 | 3.951E-03 | 1.720E-04 |
| Floor | 200 m | 300 m | 400 m | |||
|---|---|---|---|---|---|---|
| Floor displacement (m) |
Story drift (m) |
Floor displacement (m) |
Story drift (m) |
Floor displacement (m) |
Story drift (m) |
|
| 1 | 1.332E-02 | 1.332E-02 | 6.356E-04 | 6.356E-04 | 7.697E-04 | 7.697E-04 |
| 2 | 2.660E-02 | 1.328E-02 | 1.908E-03 | 1.273E-03 | 1.530E-03 | 7.630E-04 |
| 3 | 4.211E-02 | 1.551E-02 | 3.918E-03 | 2.010E-03 | 2.165E-03 | 6.350E-04 |
| 4 | 5.756E-02 | 1.545E-02 | 6.665E-03 | 2.747E-03 | 2.604E-03 | 4.390E-04 |
| 5 | 7.106E-02 | 1.350E-02 | 1.006E-02 | 3.391E-03 | 3.161E-03 | 5.570E-04 |
| 6 | 8.253E-02 | 1.147E-02 | 1.399E-02 | 3.939E-03 | 3.827E-03 | 6.660E-04 |
| 7 | 9.367E-02 | 1.114E-02 | 1.847E-02 | 4.476E-03 | 4.331E-03 | 5.040E-04 |
| 8 | 1.055E-01 | 1.183E-02 | 2.351E-02 | 5.039E-03 | 4.988E-03 | 6.570E-04 |
| 9 | 1.137E-01 | 8.200E-03 | 2.909E-02 | 5.584E-03 | 5.551E-03 | 5.630E-04 |
| 10 | 1.169E-01 | 3.200E-03 | 3.515E-02 | 6.056E-03 | 6.202E-03 | 6.510E-04 |
| 11 | 1.183E-01 | 1.400E-03 | 4.145E-02 | 6.298E-03 | 6.802E-03 | 6.000E-04 |
| 12 | 1.228E-01 | 4.500E-03 | 4.766E-02 | 6.213E-03 | 7.403E-03 | 6.010E-04 |
| 13 | 1.262E-01 | 3.400E-03 | 5.369E-02 | 6.031E-03 | 7.993E-03 | 5.900E-04 |
| 14 | 1.268E-01 | 6.000E-04 | 5.957E-02 | 5.873E-03 | 8.537E-03 | 5.440E-04 |
| 15 | 1.300E-01 | 3.200E-03 | 6.522E-02 | 5.656E-03 | 8.981E-03 | 4.440E-04 |
| 16 | 1.318E-01 | 1.800E-03 | 7.066E-02 | 5.443E-03 | 9.286E-03 | 3.050E-04 |
| Floors | 200 m | 300 m | 400 m | |||
|---|---|---|---|---|---|---|
| Floor displacement (m) |
Story drift (m) |
Floor displacement (m) |
Story drift (m) |
Floor displacement (m) |
Story drift (m) |
|
| 1 | 1.747E-02 | 1.747E-02 | 1.032E-02 | 1.032E-02 | 9.318E-03 | 9.318E-03 |
| 2 | 3.345E-02 | 1.598E-02 | 1.883E-02 | 8.510E-03 | 1.700E-02 | 7.682E-03 |
| 3 | 5.077E-02 | 1.732E-02 | 2.541E-02 | 6.580E-03 | 2.294E-02 | 5.940E-03 |
| 4 | 6.259E-02 | 1.182E-02 | 3.078E-02 | 5.370E-03 | 2.779E-02 | 4.850E-03 |
| 5 | 7.113E-02 | 8.540E-03 | 3.891E-02 | 8.130E-03 | 3.513E-02 | 7.340E-03 |
| 6 | 8.330E-02 | 1.217E-02 | 4.406E-02 | 5.150E-03 | 3.978E-02 | 4.650E-03 |
| 7 | 9.224E-02 | 8.940E-03 | 4.607E-02 | 2.010E-03 | 4.159E-02 | 1.810E-03 |
| Floor | 200 m | 300 m | 400 m | |||
|---|---|---|---|---|---|---|
| Floor displacement (m) |
Story drift (m) |
Floor displacement (m) |
Story drift (m) |
Floor displacement (m) |
Story drift (m) |
|
| 1 | 2.792E-02 | 2.792E-02 | 7.540E-03 | 7.540E-03 | 4.472E-03 | 4.472E-03 |
| 2 | 5.542E-02 | 2.750E-02 | 1.497E-02 | 7.430E-03 | 8.880E-03 | 4.408E-03 |
| 3 | 7.809E-02 | 2.267E-02 | 2.110E-02 | 6.130E-03 | 1.251E-02 | 3.630E-03 |
| 4 | 9.368E-02 | 1.559E-02 | 2.530E-02 | 4.200E-03 | 1.501E-02 | 2.500E-03 |
| 5 | 1.132E-01 | 1.952E-02 | 3.056E-02 | 5.260E-03 | 1.814E-02 | 3.130E-03 |
| 6 | 1.370E-01 | 2.380E-02 | 3.700E-02 | 6.440E-03 | 2.194E-02 | 3.800E-03 |
| 7 | 1.547E-01 | 1.770E-02 | 4.174E-02 | 4.740E-03 | 2.478E-02 | 2.840E-03 |
| 8 | 1.781E-01 | 2.340E-02 | 4.804E-02 | 6.300E-03 | 2.852E-02 | 3.740E-03 |
| 9 | 1.978E-01 | 1.970E-02 | 5.337E-02 | 5.330E-03 | 3.169E-02 | 3.170E-03 |
| 10 | 2.210E-01 | 2.320E-02 | 5.963E-02 | 6.260E-03 | 3.541E-02 | 3.720E-03 |
| 11 | 2.424E-01 | 2.140E-02 | 6.541E-02 | 5.780E-03 | 3.884E-02 | 3.430E-03 |
| 12 | 2.639E-01 | 2.150E-02 | 7.120E-02 | 5.790E-03 | 4.227E-02 | 3.430E-03 |
| 13 | 2.851E-01 | 2.120E-02 | 7.692E-02 | 5.720E-03 | 4.567E-02 | 3.400E-03 |
| 14 | 3.048E-01 | 1.970E-02 | 8.223E-02 | 5.310E-03 | 4.882E-02 | 3.150E-03 |
| 15 | 3.211E-01 | 1.630E-02 | 8.662E-02 | 4.390E-03 | 5.143E-02 | 2.610E-03 |
| 16 | 3.324E-01 | 1.130E-02 | 8.667E-02 | 5.000E-05 | 5.323E-02 | 1.800E-03 |
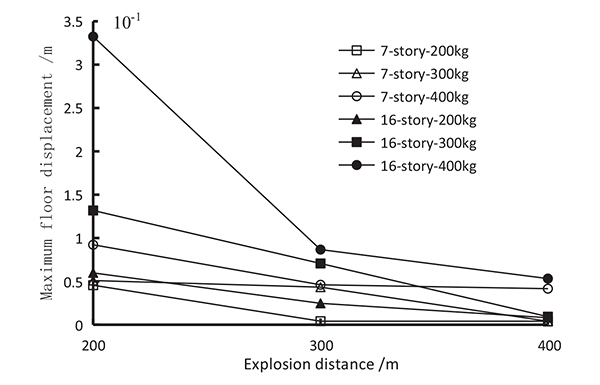
From Tables 5 to 10, the maximum floor displacements of 7-story and 16-story frame structures can be obtained and the results are shown in Fig. (3).
According to Tables 5 and 6, the vibration response of the top story is maximum under the action of blasting wave. Fig. (3) shows that with the increase of the explosion distance, the blasting vibration response decreases.
From the Tables 5 and 6, the biggest story drift of 7-story frame structure appear on the 2nd story, 7th story and 1st story under the action of 200 m, 300 m and 400 m explosion distance; and the biggest story drift of 16-story frame structure all appear on the 10th story under the action of 200 m, 300 m and 400 m explosion distances.
The maximum story drifts of 7-story and 16-story frame structures are shown in (Fig. 4).
From Fig. (4), the story drifts of 7-story and 16-story frame structures are the maximum under the action of 200 m explosion distance. With the increase of explosion distance, the story drifts gradually reduce. At the distance of 200 m when the amount of explosion charge is 300 and 400 kg, the story drifts of 16-story are all bigger than that of the 7-story. While at the distance of 300 and 400 m when the amount of explosion charge is 300 and 400 kg, the story drifts of 7-story are all bigger than that of the 16-story. And when the amount of explosion charge is 200 kg, the corresponding results of the two structures are on the contrary at different distances. It indicates that the amount of explosion has a greater impact on the story drifts when the explosion distance is small and the height of the structer becomes the main factor as the explosion distance increases. When the amount of explosion charge is 200 kg, the explosion distance has bigger influence on the lower structure. According to the existing codes in China, the inter-story displacement angle of frame structure is less than 1/550 by analyzing the results, the 7-story and 16-story frame structures can't be damaged under the action of 200 m, 300 m and 400 m explosion distances.
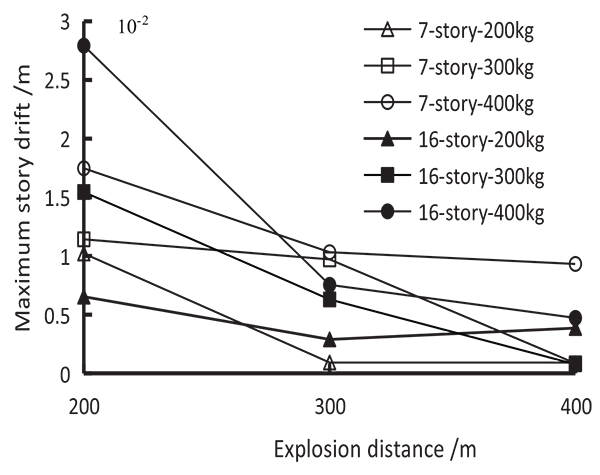
As can be seen from Figs. (3 and 4), under the same explosion source distance, the lower the structure height, the greater the maximum displacement of the floor, the story drift of the lower structure caused by the explosion is often greater than the higher structure. The maximum floor displacement and maximum story drift caused by blasting vibration are all weakened with increase of explosion source distance.
4.2. Seismic Deformation Checking
Under the action of frequent earthquake, the floor displacement should satisfy the following formula:
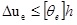 |
(6) |
Where Δue is the maximum floor displacement of the structure produced by the standard value of the frequent seismic action, in the frame structure, [θe]= 1/550, h is the height of the frame structure.
Table 11 list the floor displacement of the 7-story and 16-story frame structures under the action of different amount of explosion and the value of Δue.
| Explosion amount (kg) |
Δue(m) | 200 m | 300 m | 400 m | |
|---|---|---|---|---|---|
| Floor displacement (m) |
Floor displacement (m) |
Floor displacement (m) |
|||
| 200 | 7-story | 3.980E-02 | 4.559E-02 | 4.088E-03 | 3.809E-03 |
| 16-story | 8.890E-02 | 5.980E-02 | 2.468E-02 | 8.109E-03 | |
| 300 | 7-story | 3.980E-02 | 5.095E-02 | 4.334E-02 | 3.951E-03 |
| 16-story | 8.890E-02 | 1.318E-01 | 7.066E-02 | 9.286E-03 | |
| 400 | 7-story | 3.980E-02 | 9.224E-02 | 4.607E-02 | 4.159E-02 |
| 16-story | 8.890E-02 | 3.324E-01 | 8.667E-02 | 5.323E-02 | |
From Table 11, we can find that the 7-story frame structure is damaged while the 16-story frame structure not at the 200m and 300m explosive distance of 200kg explosive amount. And we can find the same phenomenon at the 300m explosive distance under the action of 300kg explosive amount and 300m, 400m explosive distance respectively under the action of explosive amount of 400kg. It means that the safe distance of the 7-story frame structure is larger than that of 16-story.
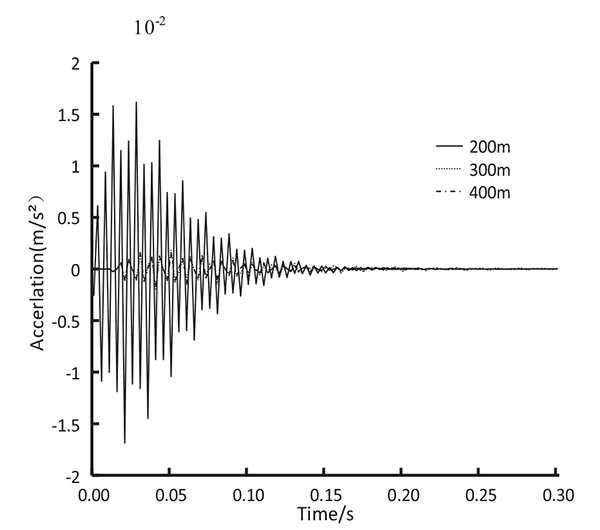
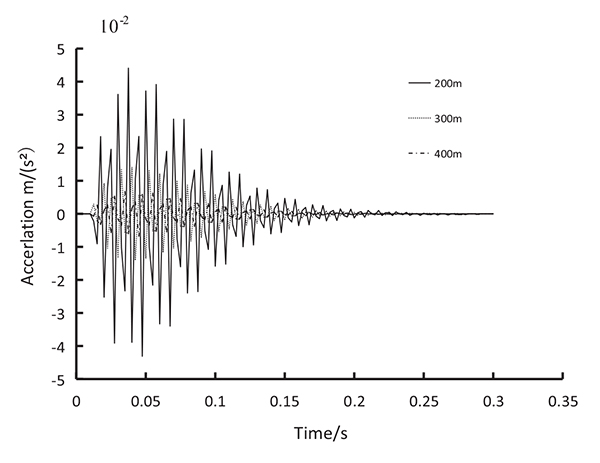
Figs. (5 to 10) show the time-history curves of acceleration on the top story at different blasting distances.

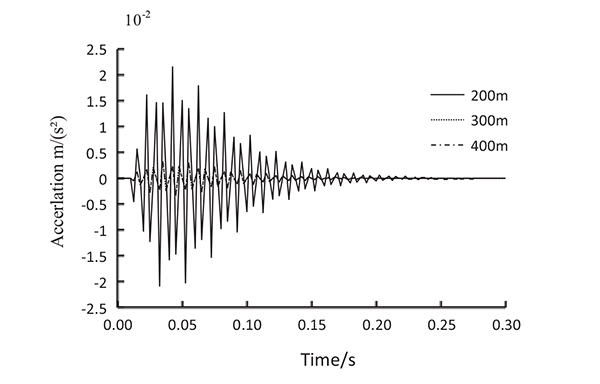
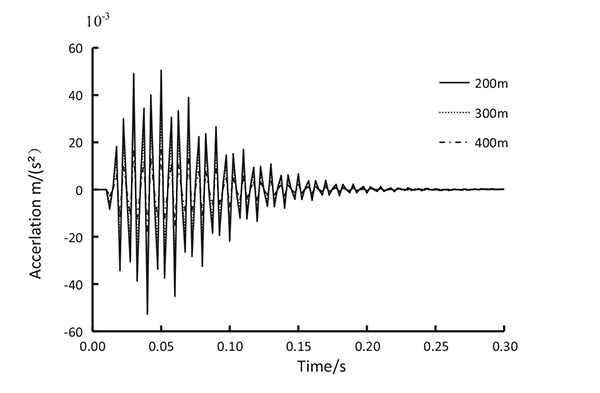
Figs. (5 to 10) show that the acceleration of top story of the frame structure caused by explosion source at 200 m is greater than at 300 m and 400 m. The maximum accelerations at the top stories of the two structures appear at approximately 0.05s under the action of different blasting seismic waves. Moreover, the acceleration amplitudes of the 7-story and 16-story are almost equal under the same amount of explosion and the same explosion distance. This result indicates that the height of building has minimal influence on the acceleration response caused by explosion.
CONCLUSION
In this paper, the variables used are the amount of explosion, the explosion source distance, the height of structure. By controlling two of the variables unchanged, the corresponding datas of the other variable are compared and analyzed. And by controlling the single variable, the corresponding datas of the other two variables respectively are compared and analyzed to summarize the relationships between the three variables on influncing the dynamic response of mining blasting vibration to surrounding reinforced concrete (RC) frame structures.
- The smaller the explosion source distance, the lower the structure, the larger the story drift, that is, in general, with the same explosive charge and small explosive source, the deformation of lower structure is larger than the higher.
- For the 7-story and 16-story frame structures, the maximum story displacement and maximum story drift of the structure are increased with the increase of the amount of explosion, and in different amount of explosion they all show that the maximum story displacement and maximum story drift of the structure are decreased with the increase of the distance from the explosion source, when the explosion source distance is large, the dynamic response of the structure is very small, even can be ignored. Therefore, a safe distance for buildings should be determined according to the situation in the mining area.
- The higher the structure is, the greater the influence of explosion source distance on the change rate of floor displacement and story drift is. The floor displacements of the two structures all have an obvious decreased trend between the explosion distances 200m and 300m. It indicates that the change rate of floor displacement is smaller when the explosion source is farther.
- Under the same explosion amount and the same explosion distance, the top acceleration amplitudes of the 16-story frame structure is larger than the those of 7-story. This result indicates that the number of stories in buildings has little influence on acceleration response caused by blasting vibration.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
This paper is a part of the national natural science foundation of China (Grant number: 51368039, 51478212), and a part of the education ministry doctoral tutor foundation of China (Grant number: 20136201110003), and a part of the plan project of science and technology in Lanzhou city (Grant number: 2014-4-94).


