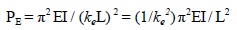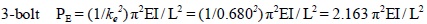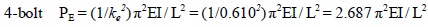RESEARCH ARTICLE
End Restraints in Steel Angles in Lattice Towers
Sriram Kalaga*
Article Information
Identifiers and Pagination:
Year: 2017Volume: 11
Issue: Suppl-2, M2
First Page: 738
Last Page: 747
Publisher ID: TOCIEJ-11-738
DOI: 10.2174/1874149501711010738
Article History:
Received Date: 25/03/2017Revision Received Date: 15/04/2017
Acceptance Date: 03/05/2017
Electronic publication date: 15/10/2017
Collection year: 2017

open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: https://creativecommons.org/licenses/by/4.0/legalcode. This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Introduction:
Test data on single angle compression members with various end connection arrangements is used to develop adjustment factors for effective buckling lengths. A connection length parameter is proposed and evaluated based on test data. Results from a total of 31 equal leg test angles with single-, double- bolts and fixed ends are used.
Methods:
Slenderness ratios considered ranged from 150 to 312. Angle sizes ranged from 38 x 38 x 3.2 (mm) to 89 x 89 x 6.4 (mm). Estimated connection lengths were about 12.5% of the member length for single-bolt joints; 24.7% for double-bolt joints and 45.6% for fixed joints. Computed effective length factors ranged from 0.544 to 0.875.
Results:
Results seem to indicate that it is possible to define and calculate connection length of a lattice tower angle member. Suggestions for incorporating connection length issues in routine designs are made.
1. INTRODUCTION
Structural steel angle members are the basic load-carrying elements in electrical transmission towers. These members are usually connected by gusset plates or directly bolted to other members through one leg. Tower joints involve single, double, triple or multiple bolted angles. The buckling or compressive strength of these angles is a function of several parameters: Bi-axial eccentricity of the loads see (Fig. 1), magnitude of restraint provided at the ends, slenderness ratios and pattern of failure either through flexural buckling or combined torsional-flexural buckling [1].
An angle strut is theoretically a restrained, eccentrically-loaded, bi-axially bent, thin-walled beam-column whose buckling load capacity is governed by end joint stiffness, and thereby, effective member length for buckling. However, the exact nature of end restraint effects in angle columns is too complex to assess [2]. Previous studies on bolted angles indicate that end connection effects are noticeable even for a single-bolted joint and that end restraints play an important role for members with slenderness ratios over 120 [3]. It was also shown that for slender 2- and 3- bolted angles, test buckling loads are consistently above theoretical values [4].
The current design procedure for tower angles is given in the ASCE Standard 10-15 [5]. The procedure defines effective slenderness in two categories: Short columns (L/r ≤ 120), controlled by eccentricity of loads; and long columns (120 ≤ L/r ≤ 250), controlled by end restraint. (See Notation for definition of parameters). Various limits on width-to-thickness ratios of angles are defined which in turn control the design compressive stress of the angle column. (See Appendix A for applicable equations).
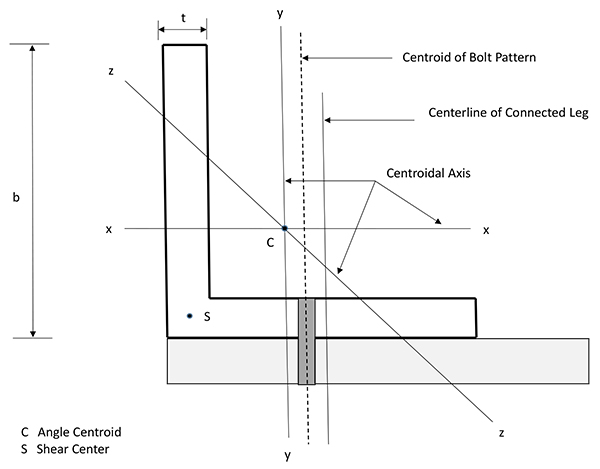 |
Fig. (1). Angle Cross Section Parameters. |
Laboratory testing of angles is generally aimed towards determining the failure or buckling load; little effort is directed towards assessing the actual connection length parameter. Part of the difficulty is related to defining what exactly constitutes the connection or how far the clamping effect of bolting extends from the bolt(s). One relatively recent study [6] proposed the concept of ‘equivalent reference length’ or ‘characteristic length’ of a connection that allows a comparison of the connection with the connected member. Such a knowledge of connection length can help form the basis for quantifying its translational and rotational stiffness and eventually develop the stiffness matrix of the connection element for inclusion into finite element programs. This paper attempts to address that issue.
The objective of this paper is to:
- Propose a definition for an angle column connection length including clamping effect of bolts
- Utilize test data on single, double and fixed-end angles to derive effective length factors
- Relate the effective length factors to connection lengths
- Propose a simple adjustment to ASCE equations for slenderness to give more accurate buckling capacities.
Only elastic buckling of equal-leg single angles with identical end connections is considered in this paper. Residual stresses and initial imperfections, although often important from buckling perspectives, are not considered here.
2. CONNECTION LENGTH
The clamping effect of the bolts in a connection is known to extend over a finite distance from the member end. Fig. (2) shows the idealization of connection and its length LC as proposed in this study and the assumed extent of the clamping zone. Each strut of length L is taken to consist of identical end connections, LC. It is obvious that connection length and the clamping effect increases with number of bolts, thus decreasing the effective member buckling length. The effective beam-column length LE is taken as center-to-center of connections. From Fig. (2):
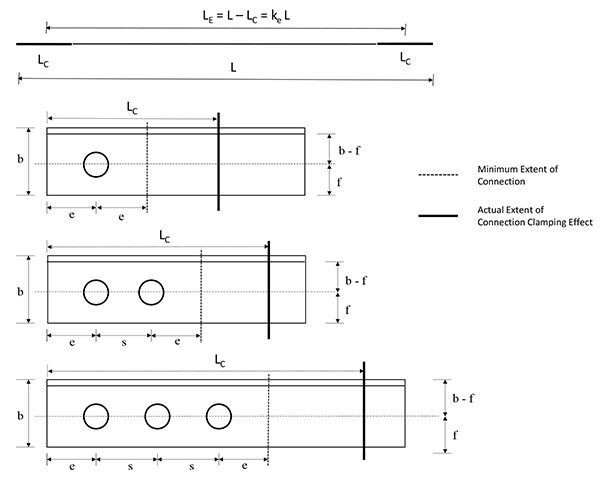 |
Fig. (2). Proposed Definition of Connection Length Parameter. |
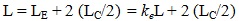 |
(1a) |
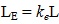 |
(1b) |
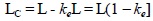 |
(1c) |
The parameter ke is an effective slenderness coefficient which quantifies the influence of connection length LC and the clamping effect.
A minimum connection length LCM can be also defined just in terms of the end distance ‘e’ and bolt spacing ‘s’.
 |
(2a) |
 |
(2b) |
 |
(2c) |
3. EFFECTIVE LENGTHS
ASCE 10-15 [5] gives the following equations for effective lengths of lattice tower angles where restraint is the controlling factor for buckling strength rather than eccentricity.
For members unrestrained against rotation at both ends:
 |
(3a) |
For members partially restrained against rotation at both ends:
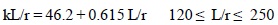 |
(3b) |
4. BUCKLING CAPACITY
The buckling capacity of an ideal, elastic column is given by the well-known Euler formula:
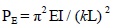 |
(4) |
For a pin-ended column, Equation (4) refers to an effective buckling length of kL = L, k = 1.
Defining Test capacity PT in terms of an effective slenderness coefficient ke:
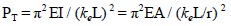 |
(5) |
where I = Ar2
Solving Equation (5) for ke, we have:
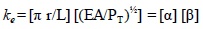 |
(6) |
Also, from Equations (4), (5) and (6):
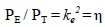 |
(7) |
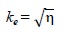 |
(8) |
Equation (1c) can be used now to determine LC.
Equations (6) to (8) facilitate a semi-empirical determination of connection length from test data.
4.1. Columns with Full End Restraint
The other extreme for a pin-ended column is a fixed-end column where both ends are fully restrained against translation and rotation. For this condition, the theoretical Euler Capacity is:
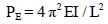 |
(9a) |
Also:
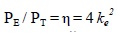 |
(9b) |
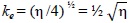 |
(9c) |
Some previous studies [2] indicate that member behavior approaches that of a fixed-ended column as the number of bolts in the end connections are increased.
4.2. Columns with Intermediate-level Restraint
Traditionally, angles with a single bolt are not considered to provide any rotational restraint [5] and are treated as pin-ended columns. Members with more than one bolt in the end connections can be considered as those with intermediate level restraint. The effective slenderness coefficient ke in this case falls in-between those of the pin-ended case and fixed case (i.e.) between Equation (8) and (9c). Since there are no guidelines to use for 2- and 3- bolt situations and beyond, the associated coefficient should be determined empirically from test data.
5. TEST DATA
Test data on thirty one (31) single, equal-leg angles is selected from published literature [7]. The test angles chosen for this study ranged from 38 mm x 38 mm x 3.2 mm to 89 mm x 89 mm x 6.4 mm (1½ in. x 1½ in. x ⅛ in. to 3½ in. x 3½ in. x ¼ in.). Slenderness ratios ranged from 150 to 312 (elastic buckling). Yield strength of steel varied from 249 MPa (36 ksi) to 322 MPa (46.7 ksi). Bolts used were 15.9 mm (⅝ in.) is diameter with all bolt holes 17.5 mm (11/16 in.) in size. All angles were tested in a manner that simulates the actual joint situation in a lattice tower (i.e.) unrestrained rotation in space. The testing setup also ensured that load is applied at an eccentricity as in a real tower. For details of the testing machine, instrumentation, loading process etc the reader is referred to the paper cited under Reference [5]. Limited test data is available for 3-bolt connections and above; some from recent research [3] exhibited bolt slip during testing and are therefore omitted.
Tables 1, 2 and 3. show the results of calculations for effective slenderness coefficient ke and connection length LC for one-bolt, two-bolt and fixed-end angles, respectively.
The minimum connection length LCM is also calculated in terms of the end distance ‘e’ and bolt spacing ‘s’ of the test specimens. These values are also shown in Tables 1 and 2.
Fig. (3) shows the variation of ke with the number of bolts in the end connection. Fig. (4) shows the variation of LC with the number of bolts in the end connection. For fixed end joints, in the absence of other guidelines, it is assumed that a 5-bolt connection simulates a state of fixity.
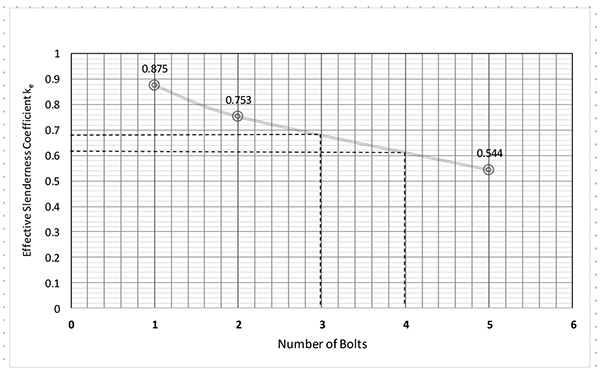 |
Fig. (3). Variations of Ke with number of bolts. |
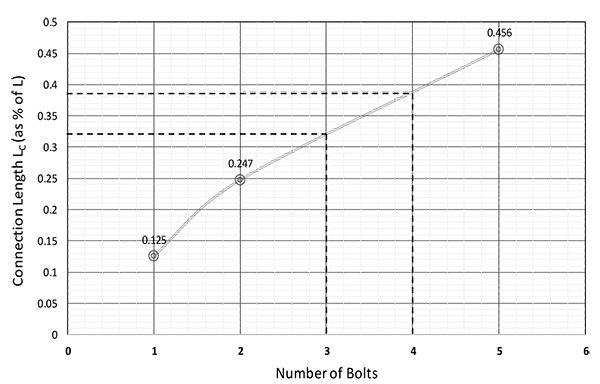 |
Fig. (4). Variations of conection length Lc with number of bolts. |
| No. | Angle Size (mm) |
Fy (MPa) |
Length L (mm) |
Area A (mm2) |
rz (mm) |
L/rz |
Fa (MPa) |
PT (kN) |
ke | LC* | LCM* |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | |
| 1 | 38 x 38 x 3.2 | 264 | 1588 | 232 | 7.52 | 211 | 58.6 | 13.6 | 0.869 | 0.066 | 0.040 |
| 2 | 38 x 38 x 3.2 | 264 | 1969 | 232 | 7.52 | 262 | 44.5 | 10.3 | 0.804 | 0.098 | 0.032 |
| 3 | 38 x 38 x 3.2 | 264 | 2350 | 232 | 7.52 | 312 | 32.1 | 13.6 | 0.792 | 0.104 | 0.027 |
| 4 | 51 x 51 x 3.2 | 264 | 2654 | 313 | 10.1 | 263 | 35.9 | 11.3 | 0.910 | 0.045 | 0.024 |
| 5 | 51 x 51 x 3.2 | 264 | 3112 | 313 | 10.1 | 308 | 27.6 | 8.6 | 0.869 | 0.065 | 0.020 |
| 6 | 64 x 64 x 6.4 | 263 | 3175 | 766 | 12.5 | 254 | 41.4 | 31.7 | 0.860 | 0.070 | 0.020 |
| 7 | 64 x 64 x 6.4 | 263 | 3797 | 766 | 12.5 | 304 | 32.8 | 25.1 | 0.807 | 0.096 | 0.017 |
| 8 | 76 x 76 x 4.8 | 322 | 3874 | 703 | 15.1 | 257 | 32.2 | 22.6 | 0.964 | 0.018 | 0.016 |
| 9 | 76 x 76 x 6.4 | 253 | 3810 | 927 | 15.0 | 254 | 37.9 | 35.1 | 0.897 | 0.051 | 0.017 |
| 10 | 76 x 76 x 6.4 | 253 | 4559 | 927 | 15.0 | 304 | 27.1 | 25.1 | 0.887 | 0.057 | 0.014 |
| 11 | 89 x 89 x 4.8 | 262 | 5321 | 824 | 17.7 | 301 | 27.6 | 30.1 | 0.891 | 0.055 | 0.0120 |
| 12 | 89 x 89 x 6.4 | 254 | 5321 | 1090 | 17.6 | 302 | 24.4 | 26.6 | 0.945 | 0.028 | 0.012 |
| Average | 0.875 | 0.063 | 0.021 |
End distance ‘e’ of all specimens = 31.8 mm (1¼ in.)
Edge distance ‘f’ of specimens = 20.6 mm to 38.1 mm (13/16 in. to 1½ in.)
| No. | Angle Size (mm) |
Fy (MPa) |
Length L (mm) |
Area A (mm2) |
rz (mm) |
L/rz |
Fa (MPa) |
PT (kN) |
ke | LC* | LCM* |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | |
| 1 | 38 x 38 x 3.2 | 260 | 1264 | 232 | 7.52 | 168 | 134.2 | 31.1 | 0.721 | 0.139 | 0.096 |
| 2 | 38 x 38 x 4.8 | 260 | 1226 | 340 | 7.45 | 165 | 161.3 | 54.7 | 0.672 | 0.164 | 0.099 |
| 3 | 51 x 51 x 3.2 | 260 | 1645 | 313 | 10.1 | 163 | 105.8 | 33.4 | 0.836 | 0.082 | 0.073 |
| 4 | 51 x 51 x 3.2 | 260 | 2153 | 313 | 10.1 | 213 | 100.0 | 31.1 | 0.661 | 0.169 | 0.056 |
| 5 | 64 x 64 x 4.8 | 265 | 1988 | 582 | 12.6 | 158 | 118.9 | 69.4 | 0.815 | 0.092 | 0.061 |
| 6 | 64 x 64 x 4.8 | 265 | 2610 | 582 | 12.6 | 207 | 95.4 | 55.6 | 0.694 | 0.153 | 0.046 |
| 7 | 76 x 76 x 6.4 | 322 | 2379 | 927 | 15.0 | 158 | 113.1 | 105 | 0.835 | 0.082 | 0.0051 |
| 8 | 76 x 76 x 6.4 | 322 | 3169 | 927 | 15.0 | 211 | 80.7 | 74.7 | 0.752 | 0.124 | 0.038 |
| 9 | 76 x 76 x 7.9 | 249 | 3118 | 1150 | 15.0 | 208 | 81.4 | 93.4 | 0.749 | 0.125 | 0.039 |
| 10 | 76 x 76 x 7.9 | 249 | 3867 | 1150 | 15.0 | 258 | 69.0 | 79.2 | 0.656 | 0.172 | 0.031 |
| 11 | 89 x 89 x 6.4 | 260 | 3626 | 1090 | 17.6 | 206 | 71.7 | 78.3 | 0.808 | 0.096 | 0.033 |
| 12 | 89 x 89 x 6.4 | 260 | 4502 | 1090 | 17.6 | 256 | 43.4 | 47.6 | 0.835 | 0.083 | 0.027 |
| Average | 0.753 | 0.123 | 0.054 |
Bolt spacing ‘s’ = 57.2 mm (2¼ in.)
End distance ‘e’ of all specimens = 31.8 mm (1¼ in.)
Edge distance ‘f’ of specimens = 20.6 mm to 38.1 mm (13/16 in. to 1½ in.)
6. DISCUSSION
As seen in Tables 1 to 3. and in Fig. (3), the effective slenderness coefficients derived from test results are consistently less than 1.00. As anticipated, the value of ke decreased as the number of bolts increased. The value obtained for the single-bolt case is 0.875; which means, contrary to assumptions that such a joint does not provide any restraint, there is a certain clamping effect associated with the bolt. For the two-bolt case, the ke value is 0.753 which indicates a larger restraint than a single-bolt. Interpolating, the following values for 3-bolt and 4-bolt cases were obtained:
3-bolt ke = 0.680
4-bolt ke = 0.610
| No. | Angle Size (mm) |
Fy (MPa) |
Length L (mm) |
Area A (mm2) |
rz (mm) |
L/rz |
Fa (MPa) |
PT (kN) |
ke | LC* | LCM* |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | |
| 1 | 76 x 76 x 4.8 | 257 | 3048 | 703 | 15.1 | 202 | 184.8 | 129.9 | 0.512 | 0.244 | Not Applicable |
| 2 | 76 x 76 x 6.4 | 253 | 2248 | 927 | 15.0 | 150 | 224.1 | 207.7 | 0.627 | 0.187 | |
| 3 | 76 x 76 x 6.4 | 253 | 2997 | 927 | 15.0 | 200 | 172.4 | 159.7 | 0.536 | 0.232 | |
| 4 | 76 x 76 x 6.4 | 253 | 3747 | 927 | 15.0 | 250 | 114.5 | 106.1 | 0.526 | 0.237 | |
| 5 | 76 x 76 x 6.4 | 253 | 4496 | 927 | 15.0 | 300 | 74.5 | 68.9 | 0.544 | 0.228 | |
| 6 | 89 x 89 x 6.4 | 260 | 3505 | 1090 | 17.6 | 199 | 155.1 | 169.0 | 0.567 | 0.217 | |
| 7 | 89 x 89 x 6.4 | 260 | 5258 | 1090 | 17.6 | 299 | 87.6 | 95.5 | 0.502 | 0.249 | |
| Average | 0.544 | 0.228 |
6.1. Connection Lengths
Connection lengths LC also proportionately increased as the number of bolts increased. From Tables 1 to 3 and in Fig. (4), the connection lengths derived from test results are consistently non-zero and clearly indicate a clamping effect. The value obtained for the single-bolt case is 0.125; which means, 12.5% of member length L and indicating a finite clamping effect associated with the bolt. For the two-bolt case, the LC value is 0.247 or 24.7% of member length L, at each end. This indicates a larger clamping effect than a single-bolt. Interpolating, the following values for 3-bolt and 4-bolt cases were obtained:
3-bolt LC = 0.320 (32% of member length L at each end)
4-bolt LC = 0.390 (39% of member length L at each end)
In comparison with the minimum connection length LCM defined in terms of end distance and bolt spacing, the actual connection lengths were between 4 to 6 times that of the value of LCM.
7. CORRELATION WITH DESIGN
To verify if the computed effective slenderness coefficients ke can be used to obtain more accurate design capacities, the parameter is applied to two test angles selected from the set used in this study. The capacity of the two angles (one single-bolted and one double-bolted) is computed using the ASCE 10-15 procedure and then adjusted using the effective slenderness parameter ke. Appendix B shows the calculations. In both cases, the angles were first assumed as having no restraint at ends (Equation 3a) and then the slenderness is modified with ke. Results show that the adjusted design capacities are very close to the test loads.
CONCLUSION
In the preceding sections, a definition for the connection length of an angle beam-column in a lattice tower is proposed where the clamping effect of the bolts is quantified. Test data on single-bolt, double-bolt and fixed-end angles is utilized to develop simple expressions for effective length factors. Connection lengths were determined from the calculated effective slenderness coefficient. For 3-bolts and above, the associated slenderness coefficient is deduced from the graph showing its variation with end restraint. The validity of making a simple modification to ASCE design equations using ke is examined.
Although modest, this study showed that it is possible to define and determine connection effects in angle columns in lattice transmission towers using carefully measured test data as a basis. Only a limited number of angle sections and slenderness ratios are studied in this paper. The results reported in this study are by no means exhaustive and further studies are warranted before the concepts discussed here can be generalized. Future investigations may include a larger database of test results, encompassing more angle sizes and slenderness levels, and effects of bolt size and connection geometries. An effort in any of those directions will be a worthwhile undertaking whose goal is to prescribe a more rational basis to the issue of quantifying end restraint effects in transmission towers and thereby more robust designs.
LIST OF NOTATIONS
| b | = Angle Leg Size |
| d | = Bolt Diameter |
| e | = End Distance |
| f | = Edge Distance |
| k | = Slenderness or Effective Length Coefficient |
| ke | = Effective Slenderness Coefficient including Connection Length and Clamping Effect |
| r | = Radius of Gyration |
| rz | = Radius of Gyration about axis z-z |
| s | = Bolt Spacing |
| t | = Thickness of Angle Leg |
| w | = Flat Width of Angle Leg including bend radius |
| A | = Area of Cross Section |
| Cc | = As defined |
| E | = Modulus of Elasticity |
| Fa | = Design Compressive Stress |
| Fu | = Specified Tensile Strength of Member |
| Fy | = Steel Yield Stress |
| I | = Moment of Inertia = A*r2 |
| L | = Length of the Member |
| LE | = Effective Length including Connection |
| LC | = Connection Length including Clamping Effect |
| LCM | = Minimum Connection Length |
| L/r | = Slenderness Ratio |
| PD | = Design Compressive Strength |
| PE | = Euler Buckling Load |
| PT | = Test Compression Capacity |
| α, β | = Derivation Parameters |
| η | = PE/PT |
| λ | = kL/r or keL/r |
| ψ | = 2.62 for MPa units and 1.0 for ksi units |
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Professor Jianguo Yang was greatly acknowledged for critically reading the manuscript.
APPENDIX A
Design Compressive Stress (Based on ASCE 10-15)
Cc = π [2E/Fy]½ (A-1)
Fa = [1 – ½ ξ2] Fy ξ= λ/Cc for λ≤ Cc (A-3a)
(w/t) max = 25
(w/t) lim1 = 80 ψ / (Fy)½ = 13.0 for 262 MPa steel, 11.7 for 322 MPa steel (A-4a)
(w/t) lim2 = 144 ψ / (Fy)½ = 23.4 for 262 MPa steel, 21.1 for 322 MPa steel (A-4b)
Design Compressive Strength = PD = A Fa
APPENDIX B
Example Calculations (Based on ASCE 10-15) Using Effective Slenderness Coefficient ke
Case 1 One-bolt Angle 64 x 64 x 6.4 (2” x 2” x ¼”)
Test # 6, Table (1)
Fy = 263 MPa (38.2 ksi). Assume E = 200 GPa (29,000 ksi)
A = 766 mm2 (1.19 in2)
Width to thickness ratio check: w/t = (64-2*6.4)/6.4 = 8 < 80 /(Fy)1/2 = 12.94
Cc =π [2E/Fy]½ = 122.7
L/r = 254
λ= kL/r = L/r = 254 (no restraint at ends)
Apply Adjustment for λ With ke Computed for Single-bolt Case.
(ke)(λ) = 0.875 * 254 = 222.25
Therefore, kL/r > Cc
Revised Fa = [π2 E] /(ke λ)2 = 39.95 MPa (5.795 ksi)
Revised Design Compressive Strength = PD = A Fa = 30.61 kN (6.88 kips)
PT = Test capacity = 31.6 kN (7.1 kips)
The revised PD containing the effective length factor ke is very close to the test load PT.
Case 2 Two-bolt Angle 76 x 76 x 6.4 (3” x 3” x ¼”)
Test # 10, Table (2)
Fy = 322 MPa (46.7 ksi). Assume E = 200 GPa (29,000 ksi)
A = 927 mm2 (1.44 in2)
Width to thickness ratio check: w/t = (76-2*6.4)/6.4 = 9.88 < 80 /(Fy)1/2 = 11.71
Cc = π [2E/Fy]½ = 110.7
L/r = 211
λ = kL/r = L/r = 211 (no restraint at ends)
Apply Adjustment for λ With ke Computed for Double-bolt Case.
(ke)(λ) = 0.753 * 211 = 158.88
Therefore, kL/r > Cc
Revised Fa = [π2 E] /(ke λ)2 = 78.18 MPa (11.34 ksi)
Revised Design Compressive Strength = PD = A Fa = 72.50 kN (16.29 kips)
PT = Test capacity = 74.7 kN (16.8 kips)
The revised PD containing the effective length factor ke is very close to the test load PT.
Note: The effective width of angle ‘w’ used in the w/t check includes the fillet radius taken as 2 times t.