Experiment Research on the Inverse Presumption Method to Evaluate Peak Temperature for Post-fire Spatial Structure

All published articles of this journal are available on ScienceDirect.

RESEARCH ARTICLE

Experiment Research on the Inverse Presumption Method to Evaluate Peak Temperature for Post-fire Spatial Structure

Jing Cui1 Lingfeng Yin1 , * Open Modal Xiaoming Guo1 Gan Tang2
Authors Info & Affiliations
The Open Civil Engineering Journal • 17 Nov 2017 • RESEARCH ARTICLE • DOI: 10.2174/1874149501711010831

Abstract

Introduction:

The peak temperature is one of the most important factors to evaluate the structural damage. Due to the reduction in the tensile strength of the steel, the structural stress is redistributed and the bearing capacity is decreased at the elevated temperature.

Methods:

This paper presents an inverse method to evaluate the peak temperature for the steel structures subjected to fire. An initial temperature field is assumed based on the post-fire structural residual displacement, and a temperature iteration function is developed to approach the peak temperature of the structure in fire by minimizing the difference between the measured and numerical results. An experimental study was conducted to investigate the structural behavior of a spatial structure subjected to fire. The temperature and displacement data were recorded.

Result and Conclusion:

Results show that the measured results have a good agreement with the predicted results, demonstrating that the proposed method in this paper is available for evaluate the peak temperature with a desirable accuracy. The inverse method of the temperature field can provide a theoretical basis for scientifically evaluating the residual displacements of the post-fire structure and formulating reliable repair and reinforcement schemes.

Keywords: Post Fire, Spatial Structure, Residual Deformations, Temperature Fields, Fire Experiment, Inverse presumption.

1. INTRODUCTION

Steel has been widely used in spatial structures. The weakness of steel is temperature sensitiveness; fire accidents in many buildings demonstrate the seriousness of this problem in recent years. Building fire is one of the common disasters in civil engineering structures. The maximum temperature directly affects the damage extent of the buildings. With the depth research on steel structure in fire, many researchers have paid attention on the residual performance and temperature inverse presumption of steel structure.

Recently many studies have focused on the mechanical properties of steel in evaluated temperature [1-4] and the performance based design of steel structure [5-7]. Due to the inhomogeneity of temperature distribution and randomness of fire spread, and the limited knowledge about steel structure in fire, the accurate method to estimate temperature is still in researching. The mostly used methods for measuring fire temperature are characteristics of surface observation method, method for determination of carbide, resilience method, ultrasonic method and so on. These methods have their own advantages, but also have disadvantages, for example, the limited detection range, low precision and so on. Inverse analysis is similar as system identification theory; according to measured data, like residual displacement and stress, to presume the material parameters and other mechanical parameters, it is widely used in civil engineering [8-10]. In thermodynamics, inverse problem of temperature has been widely used in studying [11-13], but there are a few papers focusing on the temperature inversion of post-fire structure.

This paper studies an inverse problem of temperature, constructs an inverse algorithm of temperature with optimization method based on the residual displacement of post-fire structure, and finally verifies the feasibility of the method with fire experiments.

2. OPTIMIZATION FUNCTION

In the evaluated temperature conditions, steel structure displacement consists of the deformation by load-deformation and by temperature deformation, so the displacement expression can be written as [14]:

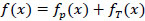(1)

where f(x) is total structural displacement, fp(x) is the displacement by load, and fT(x) is structural displacement by temperature load.

fp(x) can be easily calculated with structural theory when structure is at room temperature. Due to steel taking into plastic status in evaluated temperature and the effect of thermal expansion, the structure can undergo large deformation, fT(x) does not have exact solutions in theory. Therefore, there is no explicit relationship between the residual deformation of post fire structure f(x) and the maximum temperature T and load P, causing great difficulty in temperature identification.

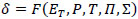Optimization method makes objective function as optimization goal, through given parameters and boundary conditions, loop iterating target function till the given accuracy is satisfied. Residual displacement of post fire structure δ is the function about material properties, load, boundary conditions, and the function can be written as:

(2)

where T is structure temperature in fire, ET is elastic modulus of material at evaluated temperature, P is load, Π is physical parameters of material at evaluated temperature, Σ is structure boundary conditions.

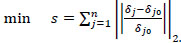As a given model, P,Σ are constant parameters, ET, Π are functions with temperature variable T. Therefore, inverse presumption of maximum temperature can be considered as an optimization problem, which is the difference s between measured displacements and FEM displacements, s can be written as:


(3)

Where δj is the measured displacement of node j, δj0 is the numerical calculation displacement of node j, and n  is the number of measuring points.

2.1. Inverse Presumption Methods

There are numbers of features of fire traces and structural residual deformation, which can be researched on maximum temperature in fire scene. The trace features include the appearance of residue, the change color of material surface, whether fireproof paint shedding or not. Structural residual deformation features include the whole structure displacement, some beams buckling, and even fracture. According to these clues, the maximum temperature experienced by the burned structure can be estimated, the temperature field distribution through interpolation method can be obtained, and using inverse presumption method to modify fire temperature distributions, until FEM results match measured deflection, the maximum temperature distribution which structure experienced can be given. Inverse method for temperature fields(IMTF) is proposed [15], and it contains four steps, the flowchart is shown in Fig. (1).

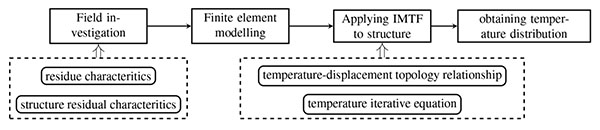
Fig. (1). Flowchart of inverse method for temperature fields.

The key steps in IMTF method are as follows:

2.1.1. Field Investigation

The residue and structural residual feathers in fire scene are clear. According to the residual deformation of post fire structure and the arrangement of measured nodes, divide the structure space into multiple regions. And estimate the possible initial temperature T(0) in each region.

2.1.2. Finite Element Model

Finite element method is one of the most effective numerical methods for engineering problems. A finite element model is established, including structural dimensions, element types, material parameters and boundary conditions.

2.1.3. Temperature-displacement Topology Relationship

The relationship between temperature and displacement is the effect of temperature change in one region on displacement of other regions. Calculate every node displacement through changing the temperature in every region. The data is stored in matrix. ∆l

2.1.4. Iteration Temperature Function

In order to find out the influence of temperature change in one region on the other regions, temperature update expression is used which is given as:

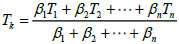(4)

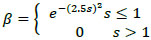where TK is the temperature of element k, βj is weight factor, which is related to the distance between element j and element k. n is number of element. β is weight function, and the expression is given as [16]:

(5)

where s is the ratio distance of calculation point and distance of origin point.

3. SPATIAL STRUCTURE FIRE EXPERIMENT

3.1. Experiment Design

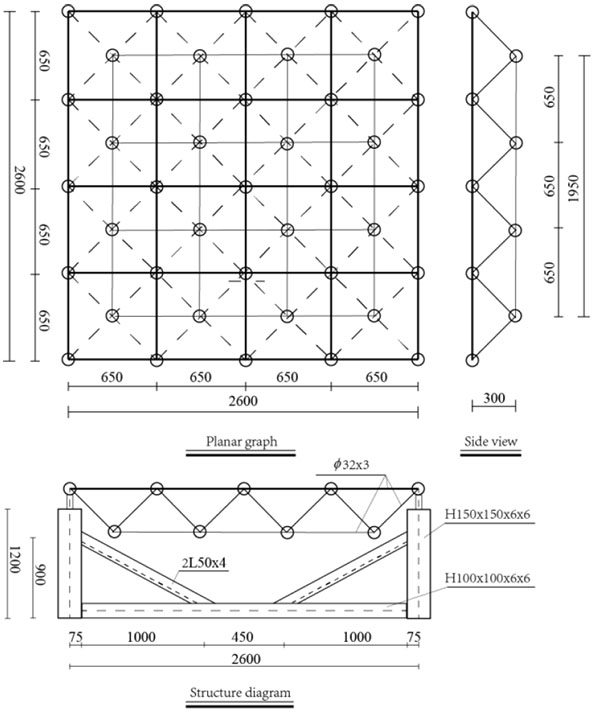
A spatial structure fire experiment is designed to verify the inverse method of temperature fields. The structure plane size is 2600mm ×2600mm, grid height is 300mm, grid spacing is 650mm. Top chords, bottom chords and web members use same steel tube ϕ32×3, and connections between chords with solder ball 100×4. And a self-balance system is designed as supporting of spatial structure in fire experiment furnace. The self-balance system is combined with H150×150×6×6 of steel columns, the beams between columns with H100×100×6×6, and diagonal bracing with dual L50×4 is designed to maintain structural stability. The design of spatial structure is shown in Fig. (2).

3.2. Test Phenomena

Spatial structure of fire experiment was tested in Southeast University. Put self-balance system in the fire test furnace, with four corners of spatial structure hinged on the system. In the test, put three concrete beams on the nodes of spatial structure, each beam quality is 153.3 kg, and average force of each node is 500.78 N. The placement of structure and loads is shown in Fig. (3). In order to ensure the stability of self-balance system, make steel column wrapped up with fire retardant cotton, the chords are bare in the air.

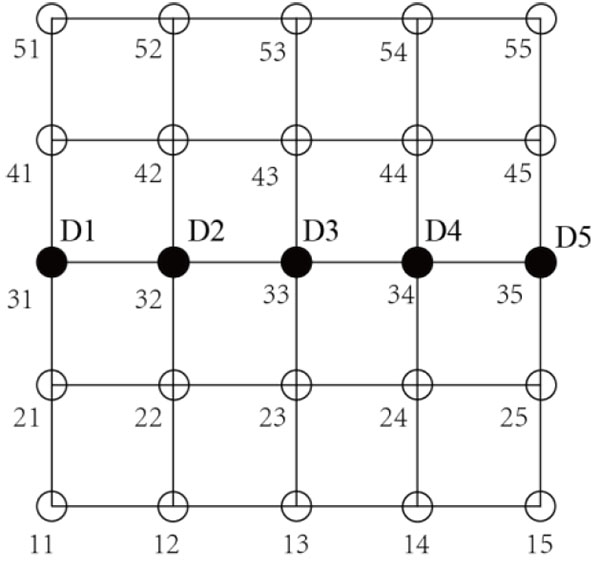
In the test process, temperature and displacements of spatial structure are recorded. There are five measured nodes on the upper chords, the arrangement of measured points is shown in Fig. (4).

Fig. (2). Design of spatial structure.
Fig. (3). Placement of structure and loads.
Fig. (4). Arrangement of displacement measured points.

The displacement response of spatial structure can be seen through the observation window on the wall of fire furnace. From the beginning, the beams did not change significantly, ten minutes later, the colors of beams changed to slight red, at that moment; the temperature in fire furnace was about 400°C. As temperature increases, the displacement of points moves along z+ direction. When the temperature of furnace achieves 800°C, then heating is stopped. In the cooling process, the displacement was slowed down along z- direction. When the temperature of furnace was close to room temperature, the cover plate was removed; obvious residual deformation of post-fire spatial structure can be observed at this stage. The time-displacement curve is shown in Fig. (5).

Fig. (5). Time-displacement curve.

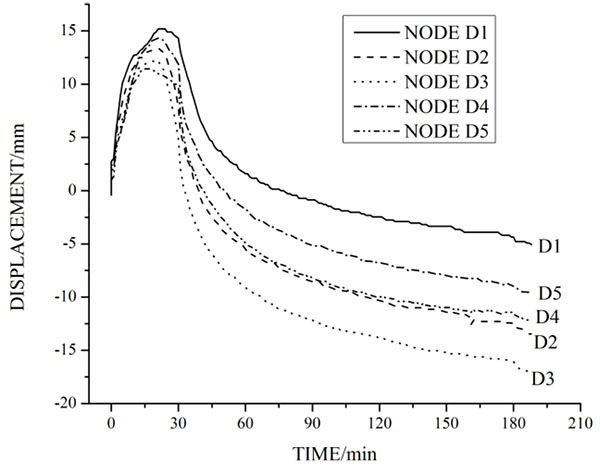
From Fig. (5), it can be observed that the change in tendency of point displacements is consistent. In the heating stage of 0~30 min, due to the effect of thermal expansion of steel in evaluated temperature, the deformation direction is z+. In the cooling stage of 30~190 min, the material properties degrade sharply, the main factor of deformation is caused by loads, and the displacement direction is z-, until the value is negative. The maximum value of displacements is point D3; the number is 33, which is in the center.

3.3. Deformation of Post Fire Structure

Total station is used to measure the node coordinates of before test and after test. The coordinates are shown in Table 1.

Table 1.
Node coordinates of before and after test/m.
Before After Changed value Before After Changed value
11 -0.320 -0.318 0.002 34 -0.335 -0.348 -0.013
12 -0.333 -0.339 -0.006 35 -0.337 -0.344 -0.007
13 -0.338 -0.348 -0.010 41 -0.332 -0.336 -0.004
14 -0.327 -0.335 0.003 42 -0.335 -0.346 -0.009
15 -0.311 -0.336 -0.009 43 -0.336 -0.350 -0.014
21 -0.332 -0.336 -0.004 44 -0.334 -0.341 -0.007
22 -0.341 -0.350 -0.009 45 -0.336 -0.339 -0.003
23 -0.343 -0.356 -0.013 51 -0.328 -0.326 -0.002
24 -0.334 -0.342 -0.008 52 -0.334 -0.339 -0.005
25 -0.330 -0.332 -0.002 53 -0.338 -0.349 -0.011
31 -0.336 -0.342 -0.006 54 -0.338 -0.347 -0.009
32 -0.338 -0.349 -0.011 55 -0.330 -0.326 0.004
33 -0.338 -0.355 -0.017

3.4. Numerical Model

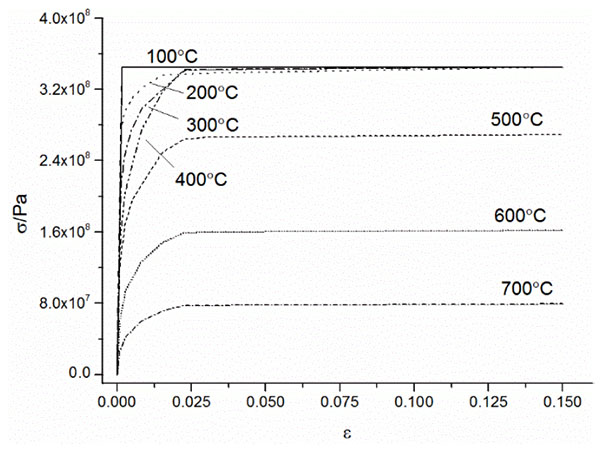
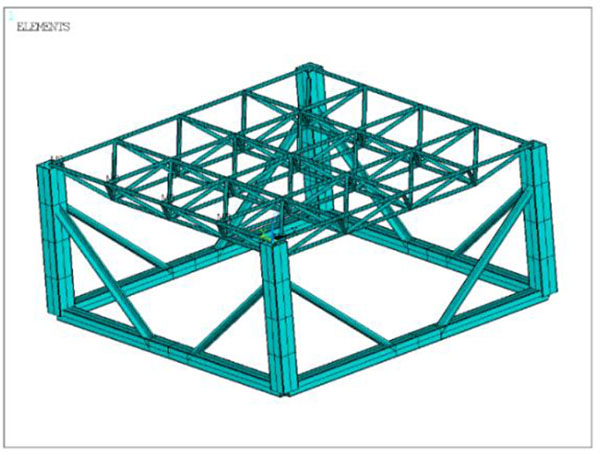
Material physical parameters of steel in evaluated temperature as shown [17]: heat transfer coefficient α=1.2×10-5, thermal conductivity cs=600J/kg°C, density ρs=7850 kg/m3,. The relationship of stress and strain of steel in evaluated temperature is shown in Fig. (6).

Fig. (6). Relationship of strain and stress.

Numerical analysis using ANSYS, simulating top chords, bottom chords with Link180, the components of self-balance system use Beam188. Constrain the x, y, z directions in bottom nodes of self-balance system. The finite element model is shown in Fig. (7).

Fig. (7). Finite element model.

3.5. IMTF Method Applied in Spatial Structure Fire Experiment

According to the residual deformation of post-fire spatial structure, the structure is divided into four regions, as shown in Fig. (8). Four displacement feather nodes are selected as A, B, C, D in Fig. (8).

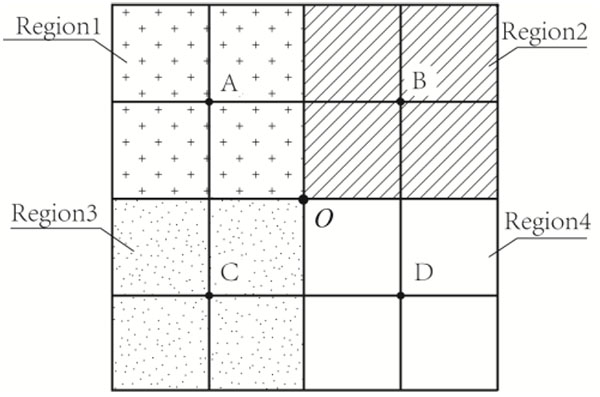
Fig. (8). Meshing map of spatial structure.

The inverse method of temperature fields was applied in post-fire spatial structure, in accordance with the calculation process mentioned in the article. Firstly, evaluating the region temperature TO. Secondly, calculating displacement-temperature topology matrix Δl(l=1,2,3,4), and the weight function β. Finally, region temperature results with IMTF method are calculated. Comparison between the measured data in test and inverse results is shown in Table 2.

Table 2.
Comparison between the measured data in test and inverse results.
Region 1 2 3 4
Test results 832.1 809.9 779.3 797.4
IMTF 864.5 836.3 46.1 762.9
Error 3.89% 3.26% 4.26% 4.22%

It can be observed that numerical results with IMTF applied in post-fire spatial structure are close to the experiment results, and the errors are all within 5%. It shows that inverse method of temperature fields is feasible to three-dimensional spatial structure, and the method can get high accuracy results.

CONCLUSION

1. In this paper, the optimization method was applied to inverse analysis of structure temperature experimented in fire, the temperature recursive function with distance weight function was constructed, and proposed the inverse presumption algorithm of temperature fields, providing a new method in temperature presumed while structure after fire.

2. Aspatial structure fire test was designed to verify the inverse method of temperature fields. The displacements of structure nodes increased along z+ direction with increase of temperature. When temperature decreased, the displacements were changed along z- direction.

3. Applying inverse method of temperature field on spatial structure, inverse calculation of the peak temperature of structure was subjected to fire through residual displacement after fire. The experiment data was compared with numerical results of IMTF to validate the feasibility of the method, and the accuracy of the results.

CONSENT FOR PUBLICATION

Not applicable.

CONFLICT OF INTEREST

The authors confirm that this article content has no conflict of interest.

ACKNOWLEDGEMENTS

This research was financially supported by the Jiangsu College Graduate Innovation Project (CXLX12_0076);A Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD1105007001); support from these sources is gratefully acknowledged.

REFERENCES

1 F. Yang, R. Song, and Y. Li, "Tensile deformation of low density duplex Fe-Mn-Al-C steel", Materials & Design, vol. 76, no. 7, pp. 32-39, 2015.
[CrossRef Link] 2 X. Qiang, F.S.K. Bijlaard, and H. Kolstein, "Elevated-temperature mechanical properties of high strength structural steel S460N: Experimental study and recommendations for fire-resistance design", Fire Safety Journal, vol. 55, no. 1, pp. 15-21, 2013. 3 K. Maruyama, K. Sawada, and J. Koike, "Strengthening mechanisms of creep resistant tempered martensitic steel", ISIJ International, vol. 41, no. 6, pp. 641-653, 2001.
[CrossRef Link] 4 L. Strassberger, D. Litvinov, and J. Aktaa, "High temperature tensile properties of oxide dispersion strengthened T91 and their correlation with microstructural evolution", Materials Science and Technology, vol. 30, no. 13B, pp. 1691-1696, 2014.
[CrossRef Link] 5 V. Kodur, M. Dwaikat, and R. Fike, "High-temperature properties of steel for fire resistance modeling of structures", Journal of Materials in Civil Engineering, vol. 22, no. 5, pp. 423-434, 2010.
[CrossRef Link] 6 N. Torić, A. Harapin, and I. Boko, "Experimental verification of a newly developed implicit creep model for steel structures exposed to fire", Engineering Structures, vol. 57, no. 12, pp. 116-124, 2013.
[CrossRef Link] 7 J. Kolšeka, M. Sajeb, I. Planincb, and T. Hozjan, "A fully generalised approach to modelling fire response of steel–RC composite structures", International Journal of Non-Linear Mechanics, vol. 67, no. 12, pp. 382-393, 2014.
[CrossRef Link] 8 V.K. Kodur, and M.Z. Naser, "Effect of shear on fire response of steel beams", Journal of Constructional Steel Research, vol. 97, no. 6, pp. 48-58, 2014.
[CrossRef Link] 9 K. Spranghers, I. Vasilakos, D. Lecompte, H. Sol, and J. Vantomme, "Identification of the plastic behavior of aluminum plates under free air explosions using inverse methods and full-field measurements", International Journal of Solids and Structures, vol. 51, no. 1, pp. 210-226, 2014.
[CrossRef Link] 10 T. Nakamura, H. Igawa, and A. Kanda, "Inverse identification of continuously distributed loads using strain data", Aerospace Science and Technology, vol. 23, no. 1, pp. 75-84, 2012.
[CrossRef Link] 11 S. Junga, and J. Ghaboussib, "Inverse identification of creep of concrete from in situ load–displacement monitoring", Engineering Structures, vol. 32, no. 5, pp. 1437-1445, 2010.
[CrossRef Link] 12 L. Bouhalaa, A. Makradia, S. Belouettara, A. Younes, and S. Natarajan, "An XFEM/CZM based inverse method for identification of composite failure parameters", Computers & Structures, vol. 153, no. 6, pp. 91-97, 2015.
[CrossRef Link] 13 A. Kaveh, and H. Fazli, "Free vibration analysis of locally modified regular structures using shifted inverse iteration method", Computers & Structures, vol. 108-109, no. 10, pp. 75-82, 2012.
[CrossRef Link] 14 G. Li, and S. Guo, "Analysis of restrained steel beams subjected to temperature increasing and descending part I:theory", Journal of Disaster Prevention and Mitigation Engineering, vol. 26, no. 3, pp. 241-250, 2006. 15 J. Cui, L. Yin, and X. Guo, "An inverse presumption method of temperature fields of spatial structure based on residual displacements", Journal of Zhejiang University (Engineering Science), vol. 50, no. 4, pp. 720-726, 2016. 16 Y. Yang, and J. Li, "A study of function in element free galerkin method", Journal of Plasticity Engineering, vol. 12, no. 4, pp. 5-9, 2005. 17 Code for Fire safety of Steel Building Structures., China Planning Press: Beijing, 2006.