All published articles of this journal are available on ScienceDirect.
Shear Strength Prediction of RC Beam-column Sandwich Interior Joints Based on Simplified Softened Strut-and-Tie
Abstract
Introduction:
The sandwich joints casted core area with weaker strength concrete of beam, has more advantages than the traditional joints casted core area with higher strength concrete of column, such as the simple construction and quality assurance, while China design codes are too simple about the sandwich joints and have no clear calculation methods.
Methods:
Due to the scarcity of rational models for predicting the strength of RC beam-column sandwich joints, a modified simplified softened strut-and-tie model suggests a more rational calculation method for the effective compressive strength and the height of the joint concrete based on the simplified softened strut-and-tie. The shear strength of existing tested 15 sandwich interior joints is calculated by using the modified simplified softened strut-and-tie model. Furthermore, the theory results are compared with those of the code method and those of the simplified softened strut-and-tie model.
Results and Conclusion:
The results indicate that the code method is more conservative, and the modified simplified softened strut-and-tie can more precisely predict the joint shear strength than that of the softened strut-and-tie model and more secure than that of the code method. Thus, the modified simplified softened strut-and-tie model can reasonable reveal the failure mechanism of RC beam-column sandwich interior joints.
1. INTRODUCTION
The strength of concrete columns is higher than the beams’ in the multi-high building structure. The column strength is cast continuous through the core area of joints in order to ensure continuity of the columns. In construction, the separate measures to the non-equal-strength junctions in the beam need to be taken [1], the columns and the core area of joints with higher strength are pouring first, then turns to the beam and slab concrete (called traditional joints) with lower strength. The construction becomes more difficult, and the fluidity of concrete is high which cannot guarantee the strength of joint core area for the vibration deficiency. The joint core area, beam and slab are simultaneously poured in construction in recent years. This construction method is series of experimental and more and more widely concerned for its advantages, such as simple, quick and easy to ensure construction quality. Theoretical researches on the sandwich joints have been studied since the 1960s. The researches out of China have carried out mainly in the way of monotonic static load experiments which chiefly focus on the calculation of the effective compressive strength fce of the joint concrete in the joint core area [2-7]. Researches in China mainly performed low frequency cyclic static load tests which focus on the seismic response analysis and the sandwich joints feasibility validation, and variations of shear semi-empirical formula are given based on the experimental results but lack of reasonable theory models’ support [8-11].
Based on strut-and-tie model, a softened strut-and-tie model which considers concrete softening is developed by
Hwang et al [12]. The applicability of this model to shear calculation is confirmed for many researches in discontinuity regions where plane hypothesis is not suitable [13, 14].
This paper investigates the accordance of the calculated formulas for the simplified softened strut-and-tie model and that for the shear strength of frame joints in China code with sandwich experimental data, then improves the simplified softened strut-and-tie model.
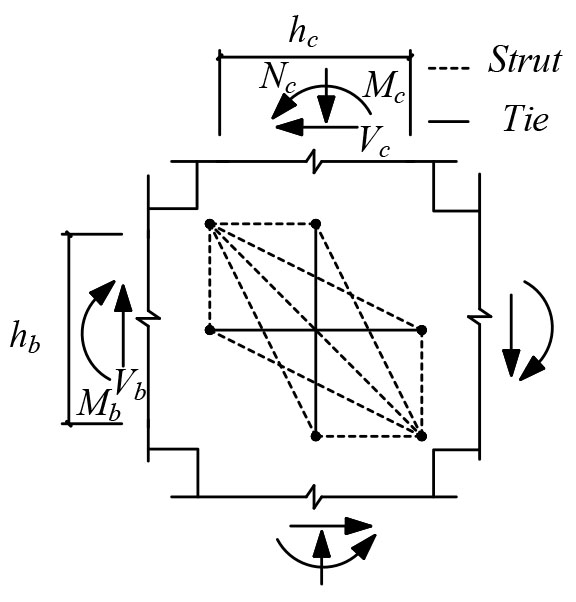
2. INTRODUCTION TO THE SIMPLIFIED SOFTENED STRUT-AND-TIE MODEL
According to the paper [12], the simplified softened strut-and-tie model satisfies the static equilibrium, the softened biaxial constitutive laws of concrete and the deformable coordination condition. It comprises diagonal mechanism constituted by diagonal strut, horizontal mechanism composed of flat strut and horizontal tie and vertical mechanism composed by steep strut and vertical tie. Strut-and-tie model is a statically indeterminate structure, the joints still hold a capacity to bear load after the tie yielding, and isn’t considered failure until the concrete in the core area reaches the compressive strength. The stress of the concrete is the sum of compressive stress for diagonal strut, flat strut and steep strut. The shear strength of the core area of joints is obtained when the acting stress exceeds the concrete strength.
The paper [12] gives a simplified calculating method for softened strut-and-tie model, as shown in Fig. (1) the formula for shear strength follows:
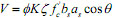 |
(1) |
Where Ø=the strength reduction ratio in value of 0.85; K= the Strut-and-Tie index; 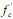 = the compressive strength of a standard concrete cylinder in units of Mpa;
= the compressive strength of a standard concrete cylinder in units of Mpa; 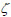 = the softening coefficient of the concrete which is approximated as;
= the softening coefficient of the concrete which is approximated as; 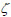 =3.35/
=3.35/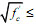 0.52; bs= the effective width of the diagonal strut which is taken the depth of the column’s section; as= the effective depth of the diagonal strut estimated by
0.52; bs= the effective width of the diagonal strut which is taken the depth of the column’s section; as= the effective depth of the diagonal strut estimated by 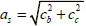 , cb= the depth of compression area of the beam obtained by taking cb=hb/5, hb=the beam depth, cc=the depth of compression area in the column obtained by taking cc=[0.25+0.85N/(Ac
, cb= the depth of compression area of the beam obtained by taking cb=hb/5, hb=the beam depth, cc=the depth of compression area in the column obtained by taking cc=[0.25+0.85N/(Ac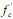 )]hc, N=the axial force acting on the column, Ac=the gross cross-sectional area of the column and hc=the thickness of the column in the direction of loading; θ=the angle between the diagonal strut and horizontal axial assumed that θ=arctan(
)]hc, N=the axial force acting on the column, Ac=the gross cross-sectional area of the column and hc=the thickness of the column in the direction of loading; θ=the angle between the diagonal strut and horizontal axial assumed that θ=arctan(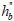 /
/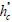 ),
), 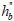 and
and 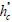 =the distance between the extreme longitudinal reinforcement in the beam and the column section respectively.
=the distance between the extreme longitudinal reinforcement in the beam and the column section respectively.
The strut-and-tie index K can be obtained as:
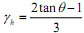 |
(2) |
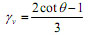 |
(3) |
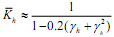 |
(4) |
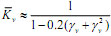 |
(5) |
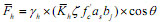 |
(6) |
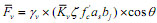 |
(7) |
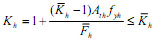 |
(8) |
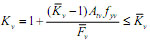 |
(9) |
Where γh= the fraction of diagonal compression transferred by the horizontal tie in the absence of the vertical tie; γv=the fraction of diagonal compression carried by the vertical tie in the absence of the horizontal tie; fyh and fyv= the yielding strengths of the horizontal and vertical rebar ties, respectively; 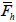 and
and 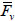 = the equilibrium forces of the horizontal and vertical ties respectively;
= the equilibrium forces of the horizontal and vertical ties respectively; 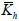 and
and 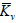 = the equilibrium constants of the horizontal and vertical ties respectively.
= the equilibrium constants of the horizontal and vertical ties respectively.
3. APPLICABILITY OF THE SIMPLIFIED SOFTENED STRUT-AND-TIE MODEL
The experiment determined the shear strengths from the sandwich interior joints tests collected in China are compared to the shear strengths predicted by the simplified softened strut-and-tie model to examine the applicability of the simplified softened strut-and-tie model. As indicated in Table 1, the ratio of test result to the average prediction for the simplified soften Strut-and-tie is 1.413 which is more conservative. Furthermore, the dispersion of the calculation results is large which indicates that the application of the simplified softened strut-and-tie model to sandwich interior joints is not suitable. Then the model needs to be modified based on shear-bearing capacity of sandwich joints.
| Refer-ence | Speci-men |
b×h (mm×mm) |
fcu,cs (MPa) | fcu,cc (MPa) | 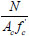 |
Area(mm2) | fyh (MPa) | fyv (MPa) | Vjh,test (KN) | Vjh,sst (KN) | Vjh,test /Vjh,sst | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Beam | Column | Ath | Atv | ||||||||||
| [8] | J-1 | 350×350 | 170×250 | 38.6 | 63.3 | 0.13 | 340 | 1419 | 227.4 | 380 | 287.3 | 178.4 | 1.61 |
| [9] | SJ-3 | 350×350 | 170×350 | 38.6 | 63.3 | 0.42 | 340 | 1564 | 381.5 | 357.6 | 843.8 | 1246.4 | 0.677 |
| SJ-4 | 350×350 | 170×350 | 38.6 | 63.3 | 0.42 | 170 | 1564 | 381.5 | 357.6 | 926.7 | 1237.2 | 0.749 | |
| SJ-3 | 350×350 | 170×350 | 38.6 | 63.3 | 0.42 | 340 | 1564 | 381.5 | 357.6 | 843.8 | 1246.4 | 0.677 | |
| [10] | JX1 | 350×350 | 170×400 | 17.1 | 40.8 | 0.42 | 2585 | 1419 | 227.4 | 380 | 963.7 | 545.4 | 1.767 |
| JX2 | 350×350 | 170×400 | 26.1 | 39.8 | 0.66 | 2607 | 1520 | 360 | 272 | 1174 | 726.9 | 1.615 | |
| JL-1 | 350×350 | 170×400 | 19.9 | 40 | 0.5 | 2462 | 1742 | 360 | 272 | 874 | 658.6 | 1.327 | |
| JDL | 350×350 | 170×400 | 20.4 | 39.2 | 0.52 | 5213 | 3040 | 385 | 293 | 1095.2 | 691.9 | 1.583 | |
| [11] | G-1 | 350×350 | 170×350 | 20.9 | 31.7 | 0.25 | 1538 | 1527 | 384 | 346 | 913 | 463.9 | 1.968 |
| G-2 | 350×350 | 170×350 | 22.9 | 36.4 | 0.42 | 1538 | 1765 | 344 | 365.6 | 951.7 | 711.8 | 1.337 | |
| G-3 | 350×350 | 170×350 | 26.1 | 33.1 | 0.45 | 1538 | 1527 | 394 | 380 | 1063.9 | 732.7 | 1.452 | |
| G-4 | 350×350 | 170×350 | 21.3 | 32.4 | 0.45 | 2307 | 2945 | 397 | 387 | 1040.7 | 673.2 | 1.546 | |
| G-5 | 350×350 | 170×350 | 21.2 | 36.6 | 0.44 | 1230 | 1527 | 397 | 368 | 847.3 | 719.9 | 1.177 | |
| G-7 | 350×350 | 170×350 | 20.7 | 41.6 | 0.3 | 1538 | 1206 | 372 | 404 | 936.2 | 601.7 | 1.556 | |
| G-8 | 350×350 | 170×400 | 20.4 | 36.8 | 0.43 | 2460 | 3484 | 350 | 377.4 | 937.2 | 658.1 | 1.424 | |
| Average value | 1.413 | ||||||||||||
| Variance | 0.109 | ||||||||||||
4. THE MODIFIED SIMPLIFIED SOFTENED STRUT-AND-TIE MODEL
4.1. The Compressive Strength of the Joints Concrete
Previous researches show that the compressive strength and ductility of the core area of sandwich joints are increased due to the confinement provided by the beam and slab, and the compressive strength can adopt the effective compressive strength fce. The results are not so much different for each fce presented in Table 2. The compressive strength of the sandwich joints concrete can be modified to the effective compressive strength which is calculated with Equation 10 given by Gamble and Klinar [4].
| Reference | Specimen | Vt/V1 | Vt/V2 | Vt/V3 | Vt/V4 | Vt/V5 | Vt/V6 | Vt/V7 |
|---|---|---|---|---|---|---|---|---|
| [8] | J-1 | 1.095 | 1.073 | 1.073 | 1.078 | 1.098 | 1.59 | 1.376 |
| [9] | SJ-3 | 0.546 | 0.546 | 0.546 | 0.546 | 0.546 | 1.922 | 1.66 |
| SJ-4 | 0.603 | 0.603 | 0.603 | 0.603 | 0.603 | 2.507 | 2.111 | |
| [10] | JX1 | 1.266 | 1.114 | 1.204 | 1.224 | 1.214 | 1.17 | 1.091 |
| JX2 | 1.229 | 1.204 | 1.178 | 1.198 | 1.247 | 1.357 | 1.279 | |
| JL-1 | 0.989 | 0.904 | 0.943 | 0.955 | 0.97 | 0.786 | 0.748 | |
| JDL | 1.195 | 1.107 | 1.143 | 1.155 | 1.18 | 0.998 | 0.95 | |
| [11] | G-1 | 1.358 | 1.323 | 1.27 | 1.312 | 1.387 | 1.14 | 1.075 |
| G-2 | 1.015 | 0.986 | 0.966 | 0.988 | 1.025 | 1.28 | 1.195 | |
| G-3 | 1.145 | 1.13 | 1.049 | 1.088 | 1.146 | 1.268 | 1.201 | |
| G-4 | 1.18 | 1.156 | 1.121 | 1.149 | 1.198 | 0.907 | 0.87 | |
| G-5 | 0.91 | 0.868 | 0.865 | 0.883 | 0.91 | 1.226 | 1.137 | |
| G-7 | 1.112 | 1.003 | 1.038 | 1.068 | 1.088 | 1.2 | 1.113 | |
| G-8 | 1.071 | 1.006 | 1.024 | 1.036 | 1.066 | 0.862 | 0.822 | |
| G-9 | 1.074 | 1.04 | 1.03 | 1.044 | 1.084 | 0.918 | 0.877 | |
| Average value | 1.052 | 1.004 | 1.004 | 1.022 | 1.051 | 1.275 | 1.167 | |
| Variance | 0.047 | 0.041 | 0.039 | 0.042 | 0.048 | 0.189 | 0.115 | |
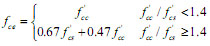 |
(10) |
4.2. The Effective Depth of the Strut
The load transferred from the compression area of the frame beam to the joint has stress diffusing in practical engineering, and the divergence angle β is 26.5 (Fig. 2).
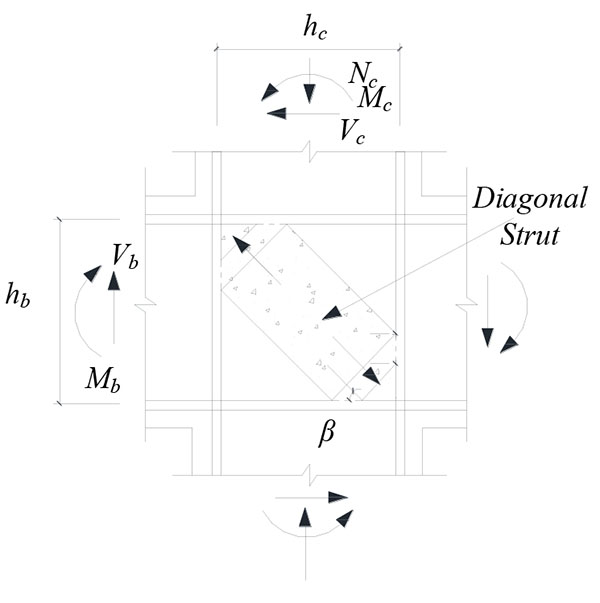
The average strength predicted by the simplified softened strut-and-tie model is lower than experiment values since the area of the strut on the sandwich joint is greater due to the compressive dispersion deeper than that of the traditional joint in core area. To validate the above-mentioned assumptions, the finite element models for G-1 as shown in Paper [11] and the corresponding traditional joint J-1 is established. The concrete core area of the traditional joint is made with the same strength concrete with the column which is different from the G-1. For the shear strengths predicted by different fce similar, the effective compressive strength in the core area of sandwich joints can be calculated by the formula given by Gamble and Klinar ( fce=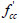 for
for 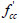 /
/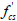 <1.4 and fce=0.67
<1.4 and fce=0.67 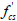 +0.47
+0.47 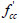 for
for 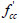 /
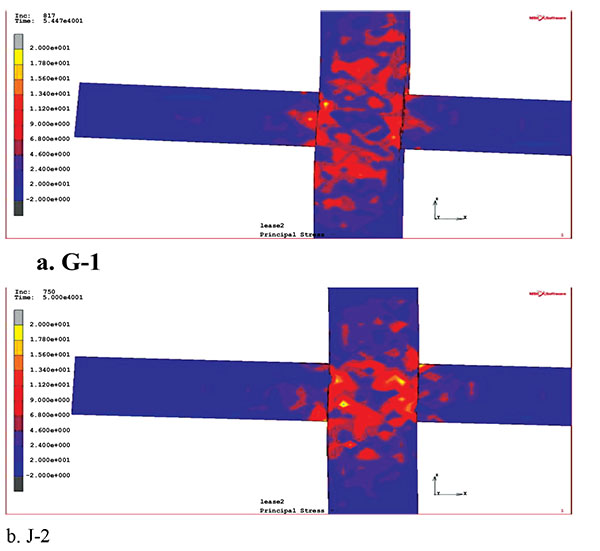
/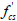 ≤1.4). The principal stress clouds are shown for J-1 with 113kN load and G-1with 104.2kN load on beam (the load ratio of 1.1) in Fig. (3). We can see that the compressive diffusion depth for core area of J-1 is smaller than that of G-1, so the core area of the sandwich is larger than traditional joint’s.
≤1.4). The principal stress clouds are shown for J-1 with 113kN load and G-1with 104.2kN load on beam (the load ratio of 1.1) in Fig. (3). We can see that the compressive diffusion depth for core area of J-1 is smaller than that of G-1, so the core area of the sandwich is larger than traditional joint’s.
Linear fitting algorithm is applied to 7 Specimens in paper [11]. It has a relatively high computation precision when the length of the diffusion length is ,ls=0.1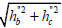 in the core area. The effective height of the diagonal strut can be modified to
in the core area. The effective height of the diagonal strut can be modified to
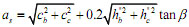 |
(11) |
4.3. Prediction Steps for the Modified Simplified Softened Strut-and-Tie Model
(1). The angle between the diagonal strut and horizontal axial θ can be obtained as θ=arctan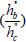 .
.
(2). Use equation (10) to calculate the effective compressive strength fce in the core area.
(3). The softening coefficient of the concrete is approximated as 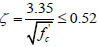 .
.
(4). The effective depth of the diagonal strut as is estimated by equation (11).
(5). The effective width of the diagonal strut bs is obtained as bs=hc.
(6). The strut-and-tie index K is gotten by Equation (2) to (9).
(7). The shear strength V for Sandwich joints can be calculated by equation (1).
5. APPLICABILITY OF THE MODIFIED SIMPLIFIED SOFTENED STRUT-AND-TIE MODEL
According to the data of accomplished experiment in China, the comparison of shear strength between prediction of results based on the simplified modified softened strut-and-tie model and test values are shown in Table 2. As indicated in Fig. (4) and Table 2, the results based on the modified simplified softened strut-and-tie model are in better agreement with experimental results than those of the simplified softened strut-and-tie model, and the difference of calculated value for each fce is similar. The results obtained by the semi-empirical formula of China current standard are smaller than test results while the prediction values gotten by the current standard formula are more closer to the test results when the compressive strength of the concrete is taken by the effective compressive strength, but not as good as prediction values by the modified simplified softened strut-and-tie model.
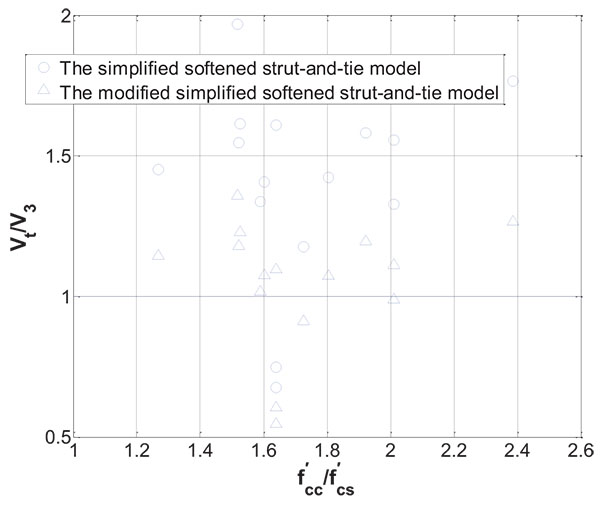
Description: V1 to V5 is in the table are the shear strength calculated by the modified simplified softened strut-and-tie model, and fce is calculated by the formula from CSAA23.3-04 [2], ACI318-2008 [3], Gamble and Klinar [4], Kayani [5], Ospina and Alexander [6] respectively; V6 is obtained by Equation 11.6.4-2 [15] of Code for design of concrete structures(China), V7 is also obtained by Equation 11.6.4-2 [15], but the compressive strength of the concrete is taken by the effective compressive strength given by Gamble and Klina.
CONCLUSION
- The predictions of shear strength for Sandwich joints according to China current concrete structure design criterion standards are smaller and uneconomic, but the prediction values obtained by the current standard formula are more similar with the test results when the effective compressive strength is taken in the joints’ core area.
- The prediction results of the sandwich joints’ shear strength calculated by the modified simplified softened strut-and-tie model agree better with the experiment results than the prediction results obtained by the simplified softened strut-and-tie model, and are even smaller than the predictions by the China standard formula when the effective compressive strength is taken for the same joints’ core area.
- The application of the Sandwich joints is restricted because China design codes are too simple about the sandwich joints and have no clear calculation methods. The modified simplified soften strut-and-tie has a definite mechanical model which can reveal reasonable force-mechanism of RC beam-column sandwich joints and can be used to calculated the shear strength.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The author(s) confirm that this article content has no conflicts of interest.
ACKNOWLEDGEMENTS
The writer gratefully acknowledges the support from National Natural Science Foundation of China (no.91315301-03, no.51378039, no.51378037) for this study.


