All published articles of this journal are available on ScienceDirect.
An Intersection Importance Estimation Method Based on the Road Network Topology
Abstract
Introduction:
The expansion of road network and continuous increase of vehicle ownership challenge the performance of routine traffic control. It is necessary to make a balanced adjustment and control from the perspective of the road network to disperse the traffic flow on the entire road network.
Methods:
This paper develops a method to quantify the intersections’ importance at a global level based on the road network topology, which is the location of the intersection in the road network and the structural characteristics of the intersection decided by the traffic movement. The priority order in traffic signal coordination is the sorting results of intersection’s importance. The proposed method consists of two consecutive algorithms. Firstly, the graph connectivity of network is defined based on the shortest path distance and spatial connectivity between adjacent intersections. Secondly, The Importance Estimation Model (IEM) is built, which is the function of the importance indexes of current intersection and its neighboring intersections. A simulated case of a six by eight grid network was employed to evaluate the effectiveness of the proposed method in TRANSYT.
Results and Conclusion:
The results show that the Importance Estimation Model (IEM) minimized the measure of effectiveness compared with the schemes obtained by the volume sorting method, the saturation degree sorting method, and the method SMOO. It also created a higher frequency of small queues than the other methods.
1. INTRODUCTION
With the economic growth and continuous expansion of cities, the number of vehicles in China and other developing countries has increased substantially. According to the statistics released by the Ministry of Public Security, as of June this year, the number of vehicles in China has reached 304 million, with an annual growth rate of over 10%. In China, there are 52 cities with more than one million vehicles, of which six are in excess of three million. The increase of vehicle ownership leads to the expansion of road network, which seriously challenges the urban traffic control system. Whatever metropolis or small cities have a common phenomenon, that is, the gathering effect of traffic flow in peak hours is obvious. It is difficult to manage the traffic flow gathering effect during the peak period by the routine control strategy of plain period. Therefore, it is necessary to improve the efficiency from the perspective of node and to improve the traffic efficiency of single junction, but also to make a balanced adjustment and control from the perspective of the road network to disperse the traffic flow on the entire road network. It is an urgent issue to study the control of traffic flow from the perspective of the entire road network, which would make more efficient use of traffic data and information and to enhance the efficiency of traffic control.
The first consideration of the operation law of traffic movement is the road network topology, which is the location of the intersection in the road network and the structural characteristics of the intersection decided by the traffic movement. The location of intersection is fixed, while the structural characteristics change with the movement of traffic flow. The traffic congestion in networks is spatially correlated in adjacent roads and it can propagate with some finite speed in time and space.
Generally, the parameter that evaluates intersection’s congestion is the saturation degree of link which is the ratio between the arrival traffic volume and the lane capacity. However, the saturation degree is a congestion index of a single intersection or link, which means it can’t reflect the propagation effect of traffic congestion in the network and can’t represent interaction between intersections. Therefore, the interconnection between adjacent intersections is studied at first. It involves two parts. The one is the physical connection characteristic that is the neighborhood between intersections. The other one is the traffic connection characteristic that is structural characteristic of traffic movements between intersections.
There is a vast literature on studying intersections’ interconnections. For instance, Yagoda et al. [1] proposed the interconnection between adjacent intersections is proportional to the volume (V), and inversely proportional to the link length (L), that is V/L. Pinnel et al. [2] found that three factors are important in determining the interconnection, which are geographic relationship, volume levels, and traffic flow characteristics. Li Ruimin et al. [3] considered five influencing factors which are distance between intersections, dispersion of traffic flow on link, major road traffic volume and its composition, and cycle length. The calculation method of every influencing factor and the fuzzy reasoning method of the factor are also introduced. Duan Houli et al. [4] thought that the interconnection was determined by the ratio of the platoon arriving in downstream intersection in green light and the platoon departing from upstream intersection, and the ratio of coordinated phase time length and cycle length. Ma Wanjing et al. [5] built a route based incidence model by taking the factors into consideration, such as the route distance, the number of signal phases, route volume distribution and queue length at approaches. Hu Hua et al. [6] put forward the model of path relevance of adjacent intersections by taking the Origin-Destination (OD) path distribution in the traffic network into consideration. Dong Chunjiao et al. [7] built a genera1 space distance model based on the space characteristic of the road network to measure the interconnection between the road sections. Shou Yanfang et al. [8] presented definition and calculation formula of interconnection based on the group decision making theory. Lu Kai et al. [9] quantified the interconnection by the traffic section volume and the cycle length, and put forward the formula of the multi-intersections combinatorial interconnection degree. Once we understand the interconnection between adjacent intersections, to quantify the intersection’s importance from the perspective of entire network would be achievable.
Some studies on quantifying the intersections’ importance have been done. The work of Lu and Wagner [10, 11] proposed a Sorting Model of Optimization Order (SMOO). But only adjacent signalized intersections are considered in their work, and the connectivity of a graph in signalized intersections doesn’t consider the distance between intersections. Atsuyuki Okabe et al. [12] developed a kernel density estimation method for estimating the density of points on a network. The case study of traffic accidents on streets in Kashiwa shows that the method can precisely estimate the density of events on a network without bias. Giovanni et al. [13] proposed the eco-routing strategy through deploying the adjoint graph in which the node weights were defined. Ventura et al. [14] designed a Colutional Neural Network (CNN) to predict the local connectivity between the central pixel of an input patch and its border points. Shuangming Zhao et al. [15] proposed a network centrality measure framework that takes into account both the topological characteristics and the geometric properties of a road network. They selected degree, betweenness, and PageRank centralities as the analysis measures. Hillier et al. [16] applied the common centrality measures of closeness and betweenness to analyze the centrality measures on the basis of segment network representations. Kazerani et al. [17, 18] studied the predictability of traffic flows using betweenness centrality, and argued that conventional betweenness centrality is unsuitable for analyzing the dynamic processes. Moreover, some studies in the field of the beam-to-column connections used in steel pallet racks also analyze the factors that play significant role to improve the design and performance [19-22].
The work presented in this paper will analyze the degree of connectivity between intersections, and determine the optimal variable of the intersections’ interaction. The paper will also analyze the traffic flow parameters which can represent the mutual influence of intersections, such as the saturation degree, the traffic volume, the link density etc. After analyzing the relationship between the road network topology and the traffic flow parameters, we build an intersection Importance Estimation Model (IEM). The importance score of node depends, to a certain degree, on the importance score of other nodes that point to it. One node has high importance score because it has lots of other nodes pointing to it, or it receives a few of incoming links while some certain very important nodes are pointing to it. The more important intersections have higher priority in traffic control, such as traffic signal coordination, and the intersection in the first order is the key intersection of the entire road network. The selection of decision variables of the importance estimation model is the basis of sub-region division. The effectiveness of the traffic signal optimization based on the intersections’ importance of intersections will be verified through traffic simulation.
These findings are of high significance for three reasons. Firstly, it is able to locate the most critical intersection of a road network at some fixed time t. Secondly, it predicts the propagation directions of congestion via calculating intersections’ importance of the next time period. Thirdly, it helps to disperse the congestion based on the prediction result of congestion propagation directions. Because for networks that satisfy certain conditions, the stationary distribution is unique and eventually will be reached no matter what the initial probability distribution.
The remainder of this paper is organized as follows: Firstly, the importance estimation model consisting of two consecutive steps of defining connectivity and computing intersection’s importance is designed and described in detail. Secondly, a simulation is made in a six by eight grid network to evaluate the method by comparing with the old method SMOO and other sort algorithms. Finally, discussion about the implementation and the applicability of the proposed model and future directions are also presented.
2. METHODOLOGY
It is generally accepted that the intersection which has highest saturation degree, which is the rule used in SCOOT and SCATS, or the largest traffic volume, or largest number of lanes is the most important intersection. Unfortunately, such a simple greedy-like sorting method arouses suspicion. Because we observe the fact that the traffic congestion has strong spatial correlation in transportation networks. This characteristic was investigated by Saeedmanesh and Geroliminis [23] via taking any road in the network and computing the standard deviation of the roads densities (speeds) up to a certain distance around it, which can be interpreted as local heterogeneity in the vicinity of that road. Here, the distance was considered as the minimum number of edges needed to connect corresponding two nodes in the graph, i.e. shortest path between two nodes. The local heterogeneity values as a function of distance for the networks of San-Francisco (heterogeneity of road densities) and Shenzhen (heterogeneity of road speeds) was depicted respectively. It was showed that the average local heterogeneity increases with the distance meaning that neighboring roads have stronger spatial correlation. The distribution of local heterogeneity has higher variance for small distances, because for small distances, high local heterogeneity can occur in areas with directional congestion or close to the borders of different clusters where different level of congestion has. This shows the necessity of searching in appropriate direction even if the average local heterogeneity is low for small distances.
Based on the above discussion, we seek to develop a method to quantify the intersections’ importance at a global level, since the aforementioned strong spatial correlation of congestion and other traffic flow parameters in road networks. That is, the importance of intersections can’t be determined by the status itself alone, but impacted by the neighboring intersections. Firstly, we define the graph connectivity neighboring intersections. This step is achieved by using Dijkstra’s algorithm, which can find the shortest path between two signalized intersections. Secondly, we build the interaction relationship among the neighboring intersections. The interaction can be expressed as a square matrix whose entries are all signalized intersections in a road network. Finally, the importance index of each signalized intersection will be computed by an estimation model, i.e. all signalized intersections get an order.
2.1. Defining Graph Connectivity
In this step, the goal is to define the graph connectivity between two signalized intersections in the network that takes into account both the shortest path distance and the spatial connectivity. As we mentioned, the connectivity between two intersections is ambiguous without clear definition. For instance, whether or not two signalized intersections that there is one or several unsignalized intersections located on the link between them have connectivity. Whether or not two signalized intersections that are spatial connected by a quite long link have connectivity. Therefore, the method to define the graph connectivity between two signalized intersections is needed and proposed here.
At first, we compute the distance of the shortest path between two signalized intersections. We model each intersection including signalized and unsignalized as a node and build their initial neighboring relationships based on their spatial connections. Specifically, the road network is abstracted as a directed graph G. Each node i in G represents an intersection in the network and the distance d(i,j) is denoted by the length of the shortest path r(i,j) from node i to j in g. The link matrix {a(i,j)} measures the spatial neighboring relation and length between each pair of nodes, with a(i,j) = 0.1 denoting that nodes i and j are adjacent and the length of directed link from i to j is 0.1 km. If nodes i and j are not adjacent or if there is only a link from j to i but no link from i to j, then a(i,j) = ∞. Thus the distance d(i,j) is calculated by Dijkstra's algorithm based on the link matrix.
Secondly, a distance threshold value θ is defined. If the distance d(i,j) ≤ θ, then there is graph connectivity from node i to j and they are neighboring nodes, and vice versa. Note that we only need compare the distance between two signalized intersections with the threshold, i.e. i, j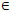
S with S denoting the set of all the signalized intersections. The graph connectivity of neighboring nodes i and j can be defined by function w(i,j) as follows in Eq. (1):
 |
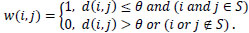(1) |
Here w(i,j) denotes there is graph connectivity from the signalized intersection i to j, while w(i,j) = 0 denotes that i to j are not connected.
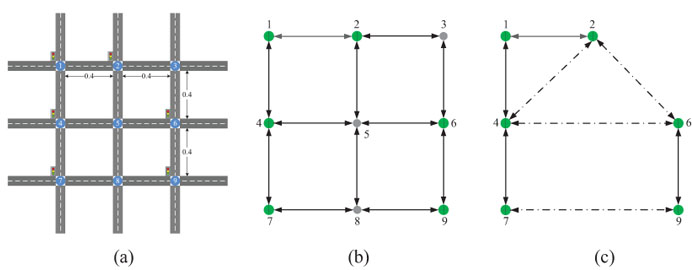
This yields the graph connectivity matrix {w(i,j)} (with only 0, 1 values) between each pair of neighboring signalized intersections. Finally, in order to further construct belief matrix of neighboring signalized intersections, we depict the connectivity by a graph. The neighboring signalized intersections that connected by a link are depicted in directed solid lines and the others are depicted in directed dotted lines. For example, a simple road network is displayed in (Fig. 1a), which including nine intersections with five signalized intersections 1, 2, 4, 6, 7, 9 and three unsignalized intersections 3, 5, 8. The lengths of all the edges between intersections are 0.4 km. We depicted the road network as a directed graph in Fig. (1b). We computed the shortest path and the distances between two signalized intersections. Suppose, the distance threshold was 0.8 km, then the connectivity of neighboring intersections is shown in Fig. (1c).
2.2. Computing Intersection’s Importance
After completing the first step, we have connectivity shape of all the signalized intersections in a road network. A model to compute the intersection’s importance was proposed. The correlation between intersections shows that the importance of an intersection is not only related to its own importance but also to its neighboring intersections’. The entire network at time t is represented by a vector or matrix, and the importance index of each intersection is the element in the matrix.
Let ri, rj represent the Importance index of intersection i,j in the priority order; larger number of r represents a more important intersection. Let Uj represents the set of neighboring intersections of intersection j. Note that the neighboring intersection has been determined by the graph connectivity in the last section. Let b represents the conditional dependency or belief of importance indexes between neighboring intersections, i.e. bij is the belief of intersection j’s importance index depending on its neighboring intersection i’s importance index. If there is a directed link from node i to node j in the connectivity graph that has been depicted in last section, then the element in the i-th row and the j-th column of the belief matrix (transformation matrix) is bi,j > 0; if there is no directed link from node i to node j, then bij = 0. And the element of the main diagonal of the belief matrix is bii = 0. Later on, it will be shown how the entries into the belief matrix can be computed from the spatial and the traffic volume of the network, right now it is assumed they have been given. Therefore, the importance indexes of all the nodes in the network can be expressed by the linear equation as follows in Eq. (2):
 |
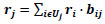(2) |
Intersections that are connected with more congested links should get a higher priority. The congestion can be reflected by the saturation degree which is the ratio of traffic volume and lane capacity q/c. Although there are models to compute the lane’s capacity, such as HCM [24], Akcelik [25], Kyte [26], Wu [27] etc., the error is unavoidable when use them in the field road. It means there are errors with the saturation degree. This fact will weaken the effect of the proposed sorting model here. Hence, we employ the more accurate parameter, traffic volume q, to increase the reliability of the sorting model by multiplying the lane’s saturation degree to traffic volume.
In the connectivity graph depicted in the last section, e.g. Fig. (1c), there are solid lines and dotted lines. The solid lines denote two neighboring nodes (signalized intersections) which are adjacent and connected by a link. So the saturation degree, traffic volume and capacity of approach lanes at downstream signalized intersections are the variables of belief. Let Ls represents the set of lanes of the direct paths (solid lines) from intersection i to intersection j; xij,l represents the lane’s saturation degree; qij,l represents the lane’s traffic volume; cij,l represents the lane’s capacity. Then, the belief of direct path from node i to node j is bijs and defined in Eq. (3 and 4) as:
 |
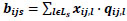(3) |
i.e.
 |
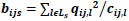(4) |
The dotted lines denote that there is no direct path between two neighboring nodes (signalized intersections) in the network, e.g. there are unsignalized intersections between them. So the turning traffic volumes, the saturation degrees and capacities of approach lanes at unsignalized intersections are variables of belief. If there are several unsignalized intersections between two neighboring nodes, the multiplication of beliefs of unsignalized intersections is needed. Let Ld represents the set of lanes of the indirect pathes (dotted lines) from intersection i to intersection j; k denotes the unsignalized intersection from node i to node j; xik,l represents the lane’s saturation degree of the unsignalized intersection k; qik,l represents the lane’s traffic volume of the unsignalized intersection k; β represents the proportion of turning movement at unsignalized intersections. Then, the belief of an indirect path from node i to node j is bijd and defined as (Eq. 5):
 |
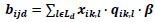(5) |
The belief of importance indexes from node i to node j (bij) is the sum of belief of direct path and indirect path, as follows in Eq. (6):
 |
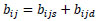(6) |
For instance, the node 5 in Fig. (1b) is an unsignalized intersection and located between node 2 and node 4, so the belief of directed link from node 2 to node 4 is defined in Eq. (7):
 |
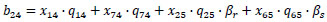(7) |
Where: x14, x74, x25, x65 are the saturation degrees of the northern and the southern approaches of intersection 4, and the northern and the eastern approaches of intersection 5;
q14, q74, q25, q65, are the traffic volumes of northern and southern approaches of intersection 4, northern and eastern approaches of intersection 5;
βr, βs, βl are the proportion of right-turning, straight-going, left-turning traffic volumes, q25 ∙ βr and q65 ∙ βs are the right-turning traffic volumes of northern approaches and the straight-going traffic volumes of eastern approaches of intersection 5.
If the number of signalized intersections in the network is n, then the beliefs between neighboring intersections form a n × n matrix B. The importance indexes of all the intersections form a non-zero column vector or n × 1 matrix R. The total importance index between the neighboring intersections is defined as follows in Eq. (8):
 |
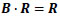(8) |
The solutions of the equation set are the values of importance indexes. Then the priority order can be sorted by the importance index. Usually the matrix B is a singular matrix, so we use the eigenvector of matrix B to denote the importance index vector R, i.e. R is an eigenvector and 1 is its eigenvalue for B. But we are primarily interested in the dominant eigenpair, which can be computed by mathematical software, or the power method. To a dominant eigenvalue, if all the entries of its dominant eigenvector are negative, the absolute function or normalization function is needed before sorting. Now, the normalized dominant eigenvalue is the importance index of each signalized intersection. The priority order of signal coordination can be computed by sorting the importance index in descending order.
3. IMPLEMENTATION
In this section, we apply and evaluate the effectiveness of our model by TRANSYT 15 [28]. At first, the priority order by the Importance Estimation Model (IEM), sorting model SMOO, the total traffic volumes sorting method, the saturation degree sorting method was computed. Secondly, the orders were inputted in the item Optimisation Order (Outline: Network Options > Optimisation Options > Advanced) in TRANSYT. At last, full run TRANSYT to optimize the traffic signal timings and calculate the measures of effectiveness. We show how the priority order improves measures of effectiveness for a hypothetical test network.
3.1. Network Description
The hypothetical test network is a 6 by 8 grid network including 38 signalized intersections and 10 unsignalized intersections. All the link length is 0.3 km, and the number of lanes is 1 lane with the free flow speed of 60 km per hour. Traffic signals are all two phases fixed-time operating on a common cycle length, in which phase 1 is for all movements on western and eastern approaches and phase 2 is for all movements on northern and southern approaches. The phase to phase intergreen time is 4 seconds. The network cycle length is optimized by Synchro 7. The traffic volumes are generated randomly in uniform distribution over the range [0,100] vehicles per hour.
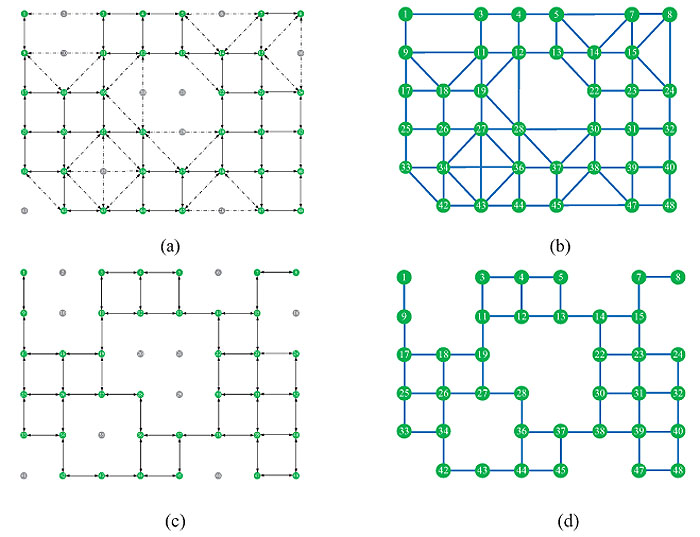
We computed the shortest path and the distances between two signalized intersections. According to the definition of the graph connectivity in section 2.1 and supposed the distance threshold is 0.6 km, the connectivity of neighboring intersections is shown in Fig. (2a). The points in red and green are the signalized intersections, and the points in grey are the unsignalized intersections. The solid line means that two nodes have connection without passing unsignalized intersections. The dotted line means two nodes have connection via an unsignalized intersection. The concise graph connectivity of all nodes and their connections is shown in Fig. (2b). If supposed the distance threshold is 0.4 km, the graph connectivity is the same with the graph connectivity by the method SMOO, shown in Figs. (2c and d). It means the distance threshold is critical to determine the graph connectivity.
3.2. Results
The priority orders by the four methods are plotted in Fig. (3). Here the IEM means the priority order sorted by the current paper, SMOO means the method in work of Lu and Wagner [12], the volume method means by the traffic volume entering intersection in descending order, and the saturation method means by the intersection’s saturation degree in descending order and the saturation degree is the maximum of intersection’s entering lanes’ saturation. The size of the point indicates intersections’ importance, the larger the size, the higher the importance. The number on the point is the exact priority order of the intersection. Fig. (3) shows that the intersection with the highest priority by IEM and SMOO are the same, which is intersection 31. The intersection with the highest priority by the volume method and is the same with the second highest priority by the saturation method, which is intersection 45.
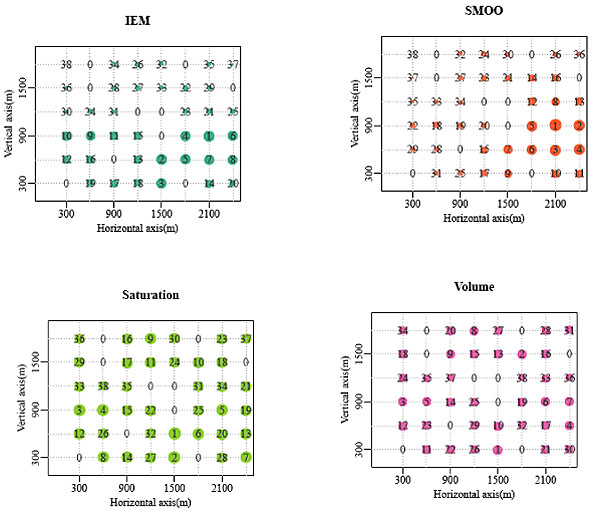
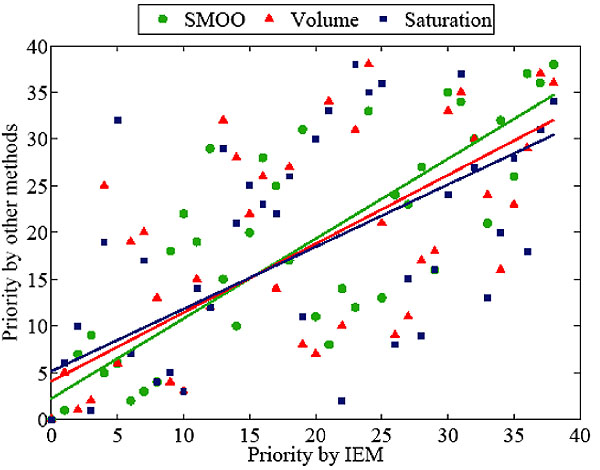
Fig. (4) displays the correlation of the priority order between the Importance Estimation Method (IEM) and the other methods. It shows that there is no high correlation among these methods. The method SMOO is closer to the revised one (R2 = 0.73) than to the volume method (R2 = 0.44) and the saturation method (R2 = 0.54), respectively. This would also explain the importance of intersection has a lot to do with the graph connectivity.
The total delay, the number of stops, and the sum of weighted cost of delay and stops (the Performance Index) are taken as the Measures of Effectiveness (MOEs). Table 1 compares MOEs of the different methods. It shows that the Importation Estimation Model (IEM) has the least delay, stops, and Performance Index. The method SMOO created more delay than the Importance Estimation Model (IEM) by 5.8%, more stops by 2.4%, more Performance Index by 5.2%. The volume method created more delay than the revised model by 7.6%, more stops by 3.3%, more Performance Index by 6.7%. The saturation method created more delay than the Importance Estimation Model (IEM) by 5.6%, more stops by 3.6%, more Performance Index by 5.5%.
| Method MOE |
IEM | SMOO | Volume | Saturation | SMOO _IEM |
Volume _IEM |
Saturation _IEM |
|---|---|---|---|---|---|---|---|
| Total delay (Veh-hr per hr) | 12.05 | 12.8 | 12.96 | 12.72 | 5.8% | 7.6% | 5.6% |
| Total stops (Stops per hr) | 3354 | 3433 | 3464 | 3474 | 2.4% | 3.3% | 3.6% |
| Performance Index ($ per hr) | 216.55 | 227.8 | 231.12 | 228.54 | 5.2% | 6.7% | 5.5% |
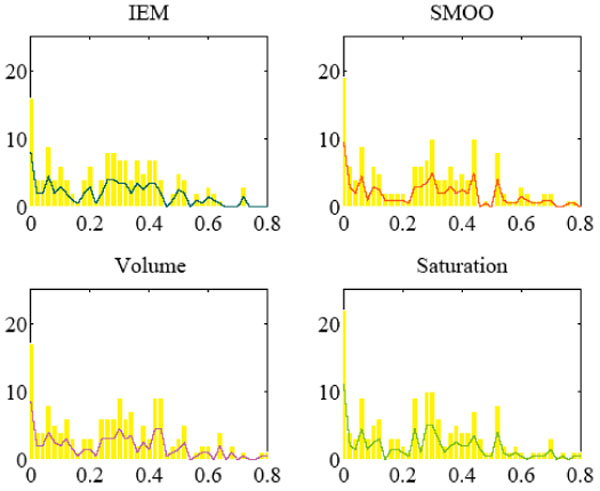
We present the histograms of the frequency of entering lane’s max queue in different methods in Fig. (5). It shows that the Importance Estimation Model (IEM) created a higher frequency of small queues. The mean value of max queue (μ) by the Importance Estimation Model (IEM) is the smallest, which is 0.2729 vehicles, and the variance (σ) is the smallest too, which is 0.0352. The mean values of max queue by the method SMOO, volume method, saturation method are 0.2781, 0.2812, and 0.2736, respectively; the variances are 0.0424, 0.0397, and 0.0427, respectively. It demonstrates that the revised method improves the queue length as compared to the other methods in the road network.
Until now we have discussed the sorting of priority of signalized intersections in a road network at a certain time period based on both traffic flow characteristics and graph connectivity. However, traffic conditions are changing during a day and the congested area may grow or shrink with time. In order to capture congestion spreading phenomena, we extend our method to the dynamic cases by repeatedly applying the Importance Estimation Model (IEM) to the next time period based on the priority sorting results of the current time period. This simple extension is based on the fact that the traffic conditions of two close time periods might be very similar. Our aim is to provide some initial evidence that the distribution of priority order can capture congestion spreading. Nevertheless, this is a difficult problem that deserves further attention.
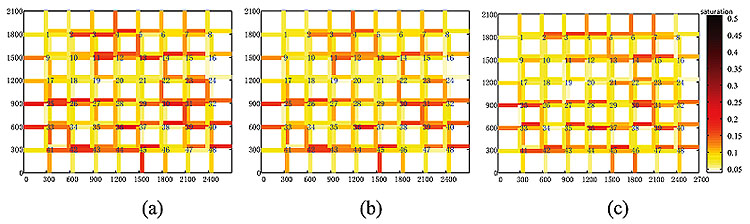
We first sort the signalized intersection’s priority at time t by the network’s graph connectivity and the importance estimation model (IEM). Then we optimize the signal plans by TRANSYT 15, and update the signal plans in simulation software of Synchro. After running simulation in SimTraffic in Synchro, we get the renewed traffic volume and saturation degree of links. Thirdly, we apply only the Importance Estimation Model (IEM) to the network with renewed volume and saturation, since the graph connectivity of network keeps the same, to get the priority order at the next period. Generally, the priority sorting result at t + i is obtained by applying the importance estimation model (IEM) to the sorting results at t + i - 1 with the renewed link volumes and saturation at t + i. In simulations, we set the initial sorting at t = 7h and repeatedly run the priority sorting model with increase step of 20 minutes until t = 8h, when the network tends to be homogeneously uncongested. The saturation degrees of links of network from t = 7h to t = 8h are shown in Fig. (6). We see clearly that the links’ saturation degree decreases with time from Fig. (6a to c). It means that the optimal priority order can help decrease the saturation of links. It also shows that the Importance Estimation Model (IEM) can capture the shift of the congested intersection.
CONCLUSION
This paper presents a method to quantify the importance of signalized intersections in a road network based on the road network topology which is the location of the intersection and the structural characteristics of traffic movement. The importance of intersection determines the priority order in traffic signal coordination. The method takes into account both the shortest path distance and spatial connectivity between adjacent intersections when defining the graph connectivity of network, which is the first step. In the second step, the Importance Estimation Model (IEM) is built, which is the function of the importance indexes of current intersection and its neighboring intersections. The solutions of the equation set are the values of importance indexes. It is the normalized dominant eigenvector of the transformation matrix of intersection importance.
The outcome of proposed method for the case study with simulated data proved it had better measures of effectiveness than the method SMOO, volume method and saturation method. The delay time, stops and queue length by the proposed method was the smallest. The outcome of the dynamic application of the proposed method proved the Importance Estimation Model (IEM) can capture the congestion, and lower the saturation degree of links. A traffic signal optimization tool, TRANSYT, was used to demonstrate the effects of the sorting model since it has a setting of optimization order. In two test cases, SMoPO turned out to compute an optimal order that brought better performance.
In the simulated case, the Importance Estimation Model (IEM) turned out to compute a priority order which led to better Performance Index (PI). When compared with the scheme obtained by a better greedy algorithm named the volume sorting method, saturation degree sorting method, and the old method SMOO, IEM minimized the network PI value by 6.7%, 5.5%, 5.2%, the mean delay per vehicle by 7.6%, 5.6%, 5.8%, the stops by 3,3%, 3.6%, 2.4% respectively. The Importance Estimation Model (IEM) also created a higher frequency of small queues than the other methods. Finally, the application of IEM in traffic signal optimization for one hour shows the optimal priority order can help disperse the traffic congestion.
As a future work, it would be challenging to build the framework from static to dynamic sorting. This approach also needs some effort in terms of distance threshold in defining graph connectivity. Another research priority is to carefully investigate the interactions clustering. While the intersection’s priority (i.e. importance) should be an important property of clusters, the shape of the clusters and also their boundaries should facilitate the control objectives. Besides, more case studies of different traffic demands and networks should be conducted to assess the effectiveness of the proposed method.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
This work has been supported by the Zhejiang Province Natural Science Foundation for Young Scientists No. LQ18F030004, Ningbo Soft Science Research Program No. 2017A10077, and K. C. Wong Magna Fund in Ningbo University.
