All published articles of this journal are available on ScienceDirect.
Probabilistic Verification of Structural Stability Design Procedures
Abstract
Introduction:
This contribution presents a comparison of three methods of the statistical computation of the design load-carrying capacity of a steel plane frame. Two approaches of the European Standard Eurocode 3 and one stochastic approach are applied. The stochastic approach takes into account the random influence of all imperfections and can be applied to the reliability verification of design according to Eurocode 3.
Methods:
The columns and beams in the steel frame are modelled with beam elements using the stability solution with buckling length and the geometrically nonlinear solution. The stochastic computational model is based on the geometrically nonlinear solution and on the random influence of initial imperfections, whose random samplings are simulated using the Monte Carlo method.
Results and Conclusion:
The design load-carrying capacity of the steel plane frame computed using the stability solution with buckling length is in good agreement with the stochastic solution in which the design value is calculated as 0.1 percentile. On the contrary, the geometrically nonlinear solution according to Eurocode 3 gives the lowest (safest) values of design load-carrying capacity.
1. INTRODUCTION
The load-carrying capacity of frames with slender columns under compression is negatively influenced by stability phenomena, which must be taken into consideration during assessment and design [1]. Eurocode 3 [2] determines the load-carrying capacity in two basic ways. The first approach requires the calculation of the buckling length, non-dimensional slenderness, and buckling coefficients. The second approach assumes the inclusion of initial imperfections, which reduce the load-carrying capacity, computed using a geometrically nonlinear solution with initial imperfections. Both of these approaches include simplifications, which in the case of the stability solution is the substitution of the influence of all imperfections with a buckling coefficient, or, in the case of the geometrically nonlinear solution with an initial geometrical imperfection. It is demonstrated in the presented paper that the design load-carrying capacity, which is computed using the concept of limit states of the Eurocode Standards [3, 4], may differ by up to 10%. This brings up the question of what degree of risk could be accepted by a designer for the ultimate limit state, and how to determine the load-carrying capacity for economic and optimum reliable design with increased accuracy.
Initial imperfections are typically considered in advanced analyses [5, 6]. Conventional methods of modelling imperfections are based on the scaling of the eigen buckling modes [7, 8]. More advanced methods consider separately the system (out-of-plumb) and the bow (out of straightness) imperfections and thereby model more accurately the shapes and magnitudes of initial curvatures obtained from the results of experimental research, see for e.g [9]. Probabilistic analysis of reliability requires the inclusion of all imperfections as random variables [10] or random fields [11]. Input imperfections with high global sensitivity to the limit states can be identified as the key variables using modern methods of sensitivity analysis [12]. The failure-probability-based sensitivity, which measures the effect of input variables on the structural failure probability, can provide useful information on reliability-based design optimization [13]. In cases where a satisfactory number of statistically applicable data is available, one of the possibilities for determining the design load-carrying capacity is by using stochastic analysis and design reliability conditions according to the European Standard EN 1990 [14].
The standard and stochastic analyses of reliability presented in this article are computed using the algorithm and software developed by the author of this paper [15, 16]. The paper links up with preceding experimental research [17, 18], research in the field of reliability theory [19-22], and decision-making methods in application to civil engineering [23, 24].
2. DESIGN LOAD-CARRYING CAPACITY
The subject of study is the steel plane frame illustrated in Fig. (1). The left column is stressed by compressive force F. The right column is stressed by compressive force δF with parameter. The meshing of the frame geometry was carried out using beam elements, where the elastic stiffness matrix and the geometric stiffness matrix were published in [8]. Each column was meshed with eighteen beam finite elements. The beam finite element, including the stiffness matrix and two geometric matrices, was published in detail in [15]. The cross beam was meshed with eight beam finite elements. It can be noted that this beam finite element has been effectively used in a number of studies [15, 16, 20, 25-27]. Steel of grade S235 was used for the numerical study performed in this article.
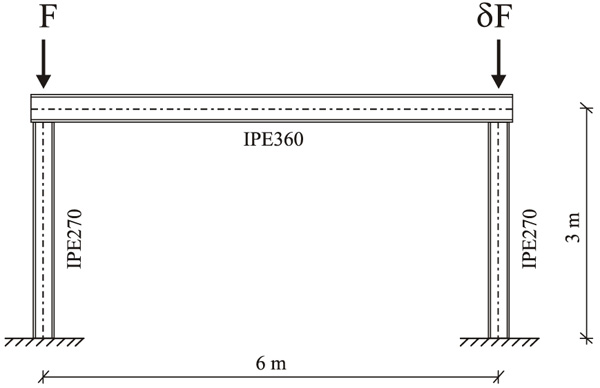
2.1. Stability Solution with Buckling Length
The stability solution with buckling length is based on the calculation of the critical load action Fcr at which the system (without imperfections) loses its stability (Table 1). Axial forces in beams intended for buckling with a displacement of joints and their respective buckling lengths correspond to the critical load action.
| δ | 1 | 0.5 | 0 |
| Lcr1 [m] | 6.7111 | 5.8181 | 4.79023 |
| Lcr2 [m] | 6.7111 | 8.2281 | ∞ |
| Fmax [kN] | 945.3 | 979.6 | 1012.5 |
The design load-carrying capacity Fmax can be determined for steel S235 according to Eurocode 3 [2]. The standard provides the calculation method of the buckling coefficient using buckling lengths Lcr1 and Lcr2. Eurocode 3 [2] further gives procedures for the computation of the design load-carrying capacity and for the assessment of the steel plane frame at the ultimate limit state. Nevertheless, it permits simplifications, which lead to larger or smaller inaccuracies in the dimensioning of beams. It is a paradox of buckling lengths that extremely high buckling lengths are obtained for columns with small axial force (see Lcr2=∞ of the right column for δ=0).
2.2. The Geometrically Nonlinear Solution
Eurocode 3 [2] makes it possible to compute the design load-carrying capacity with the use of the geometrically nonlinear solution with consideration to the influence of all imperfections. The imperfections include system imperfections (out-of-plumb) and bow (out-of-straightness) imperfections of the columns under compression (Fig. 2).
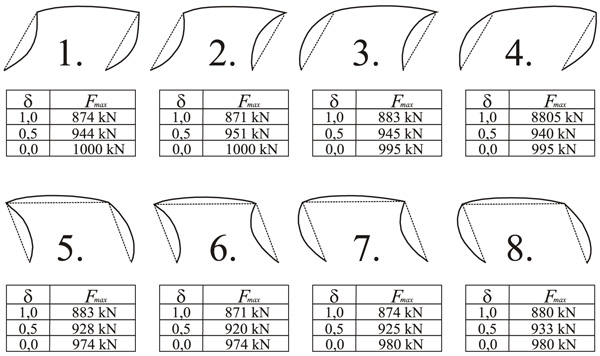
The load-carrying capacity was determined using the Euler method in combination with the Newton-Raphson method. The bow imperfection was introduced in the shape of a half-wave of the sine function with a so-called equivalent amplitude e0 = 9.33 mm [2]. The out-of-plumb imperfections were introduced as 1:200 of the height of the frame [2, 25]. The out-of-plumb or out-of-vertical imperfections can be applied in all horizontal directions but were considered in only one direction [2]. The frame can be solved using eight imperfections of frames (Fig. 2). Eight variants of imperfections yield different values of the design load-carrying capacity, the maximum and minimum values being interesting (Table 2).
| δ | 1 | 0.5 | 0 |
| Minimum Fmax [kN] | 870.6 | 920 | 974.1 |
| Maximum Fmax [kN] | 883.2 | 951.1 | 1000 |
| difference [%] | 1.4 | 3.4 | 2.7 |
For more complicated systems with more beams, it is not possible to study all combinations of bow and out-of-plumb imperfections, and differences between the minimum and maximum load-carrying capacities can be more significant.
2.3. The Stochastic Analysis According to Standard EN1990
According to EN1990 [14], one of the possibilities for determining the design load-carrying capacity is the application of the statistical solution with consideration to the random influence of all imperfections. Stochastic models of the geometrical imperfections of the frame in Fig. (1) were published in [26, 27]. It was assumed that the initial bow curvature of the column in the shape of a one-half wave of the sine function with e0 would have a Gauss probability density function with zero mean value and standard deviation Se0=1.5 mm. This probabilistic model is based on the rule 2Sx, i.e, that 95% random realizations lie within the interval ±L/1000=0.003 m. Out-of-plumb imperfections of the columns are introduced with Gauss pdf with zero mean value; the standard deviation was introduced using the method described in [27]. The principle of forming stochastic combinations (random realizations) of initial imperfections is explained in detail in [27] (Fig. 3).
The statistical characteristics of imperfections of cross-sectional dimensions were introduced according to the results of experimental research [17, 18]. The yield strength of steel grade S235 was introduced as a random variable with normal probability distribution with mean value mfy=297.3 MPa and standard deviation Sfy=16.8 MPa [17]. The residual stress was not considered. An ideally elastic-plastic material without hardening was considered. The influence of deviations of physical-mechanical characteristics was taken into account by the variability of Young’s modulus E, the mean value was considered as mE=210 GPa and standard deviation SE =10.5 GPa [28]. The residual stress was not considered.
The geometrically and materially nonlinear solution was chosen for the computational model [17]. Statistical analysis was performed for two hundred thousand runs of the Monte Carlo method. F due to which the yield strength is reached in the most stressed point of the web of the left or the right column was calculated in each run of the Monte Carlo method. The random variability of the load-carrying capacity is due to the random variability of initial imperfections. For design reliability index βd = 3.8, the design load-carrying capacity can be computed as 0.1percentile [14]. Reliability index β has a target value of 3.8 provided that we consider the ultimate limit state for common design situations within the reference period of 50 years [29]. The design reliability index βd = 3.8 can be used for medium consequences of loss of human life, economic, social or environmental consequences. The one hundredth lowest load-carrying capacity from the statistical set of sampling (runs) of load-carrying capacities sorted in ascending order can be considered as the estimate of the design value. The design load-carrying capacity computed as 0.1 percentile [14] is an alternative to the approaches of the standard [2].
| δ | 1 | 0.5 | 0 |
| 0.1 percentile [kN] | 949.9 | 984.4 | 1016.6 |
A graphical summarization of the design values of the load-carrying capacity is shown in Fig. (4) and Table 3. It is evident that the safest design having the lowest load-carrying capacity is reached using the geometrically nonlinear solution given in Chapter 2.2. This design also contains certain subjective uncertainty, which is introduced by the engineer when choosing the shape of the imperfection from Fig. (2). Selection of the shape of the imperfection gives a certain freedom in design in which the engineer may reflect the effort for the lightest structure (economic aspect) or the effort for a robust structure (safety aspect). In the case of complex steel structures with an equivalent number of columns and beams, the differences between the load carrying capacities due to the subjective selection of the shape of the imperfection may be even more significant, thus, design using the geometrically nonlinear solution must be approached with the utmost caution and responsibility.
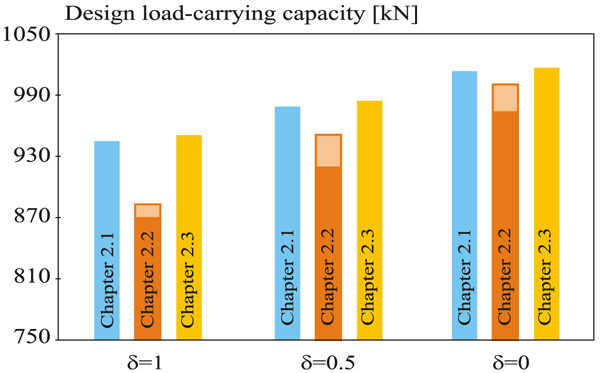
The stochastic solution leads to approximately similar results as the stability solution with buckling length Fig. (4). The stability solution with buckling length is well established in engineering practice and in the case of the presented analysis is shown to be in good agreement with the design reliability conditions of the Standard EN1990 [14]. In the stochastic solution, refinement of the shape of the initial curvature of the column can be discussed, for e.g. using random fields [11]. Modelling using random fields can refine the load-carrying capacity if the non-dimensional slenderness of the columns is close to one. However, knowledge of the correlation length is necessary. Moreover, greater influence can be expected from the out-of-plumb imperfections [27]. One way to evaluate the influence of initial imperfections is to apply sensitivity analysis methods [30, 31].
CONCLUSION
The safety and reliability of structural design according to Eurocode 3 [2] based on the concept of limit states require optimally set values of the partial safety factors. Design according to the Eurocode Standards is a compromise between economy and reliability of supporting structures and should be satisfactory for the majority of common design situations. Nevertheless, higher or lower safety and reliability can be required in some cases, which may be achieved using a design based on the stochastic calculation of design values. The paper discusses the stochastic computation of the design load-carrying capacity as 0.1 percentile for design reliability index of medium (standard) value βd = 3.8. This reliability was applied to verify the design reliability of the load-carrying capacity calculated according to EC3 [2]. It was found that the design load-carrying capacity calculated as 0.1 percentile is in relatively good agreement with the design load-carrying capacity obtained using the stability solution with buckling load. The lowest design load-carrying capacity (the highest design reliability) was obtained using the geometrically nonlinear solution with initial imperfections. The conclusions reached are formulated on the basis of the results of one example of a steel plane frame and additional reliability analyses are necessary for the formulation of more general conclusions. From a long-term point of view, it is necessary to strive for the continuous study of material and geometrical characteristics of steel products by experimental research, because they provide important inputs for reliability analysis.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The author declares no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
The article was elaborated within the framework of project GAČR 18-13212S.


