All published articles of this journal are available on ScienceDirect.
Effect of Rebar on Ductility of Moment-resisting Frame with Concrete-filled Tube Column
Abstract
Background:
Today, many developed countries use the Concrete-Filled Steel tube columns (CFT) to construct high-rise building and bridge piers.
Objective:
This paper investigates the effect of rebar inside the concrete core of CFT columns.
Materials and Methods:
For this purpose, the structural performance of three two-span frames is evaluated with ABAQUS software. The frames vary based on the presence or absence of rebar within the concrete core, so that the first model has no rebar, the second model has less rebar, and the third model has more rebar inside the concrete core.
Results and Conclusion:
The observations from the hysteresis curves obtained from the analyses suggest the more ductile behavior, greater stiffness, and higher energy dissipation potential in the third model relative to the other two models, so that the third model has about 24% more energy absorption capacity than the case without the rebar.
1. INTRODUCTION
Today, the Concrete-Filled Steel tube columns (CFT) are widely used in many developed countries. In these columns, the steel tube acts as the concrete core mold and also prevents the corrosion and abrasion of concrete, and the concrete prevents the local buckling of the steel tube wall. In addition, due to the difference in Poisson's ratio between the steel and the concrete, increasing the volume of concrete core due to the propagation of cracks is restricted by the steel tube, which increases the strength and ductility of the concrete. In general, CFT columns have high axial load capacity, better seismic performance, greater ductility, and higher energy absorption capacity [1]. In contrast to the reinforced concrete (RC) structures, the CFT members change the building requirements. This is associated with the reduced construction time and manpower, which is a particular advantage in the construction. It is also important to build the bridges as fast as possible, because most of the recent constructions are performed in the presence of existing traffic, which has many safety risks and social and economic costs [2].
Several studies have been conducted in this field. Schneider (1998) conducted an experimental and analytical study on 14 samples of short CFT columns under the axial loading. Three samples with the circular cross-section, five samples with a square cross-section and six samples with rectangular cross-section were selected. Also, the finite element models with ABAQUS software were developed and validated using the experimental results, and the results indicated the axial ductility of most circular sections compared with other sections [3]. Zhang et al. (2013) studied the compressive load-bearing capacity of a concrete-filled square steel tube reinforced with a circular steel tube from inside, and found that the bearing capacity in these columns is improved by 20% compared to the composite column without the internal circular steel tube in the same cross-section. As a result, these columns can be used to significantly reduce the column dimensions, which leads to the economical savings and the increased load-bearing capacity [4]. Younes et al. (2015) performed the laboratory investigation of the CFT columns with small dimensions using the shear connectors and examined their effects. They found that the use of connectors increases the axial capacity of the CFT columns, and the closer the connectors, the greater the capacity of these columns. The reason for this is the increase in the transfer of load to steel tubes due to the increased number of connectors [5]. Han et al. (2007) examined the performance of the thin-walled concrete-filled steel tube columns under pure torsion. The ABAQUS software was used for the finite element analysis and the results were in good agreement with the experimental results of previous researchers, and eventually led to the development of the formulas for calculating the ultimate torsional strength and the torsional moment-strain curves for the composite columns [6]. Spyrakos et al. (2012) examined the complex response of RC frames and brick infill walls strengthened with Fiber Reinforced Polymers. By comparison of results, conclusions are drawn concerning design proce-dures [7]. Tao et al. (2013) evaluated the finite element model of CFT columns under the axial load and, given the confinement of concrete core by the steel tube, stated that it is challenging to model the concrete behavior in these columns and requires careful consideration. Although significant efforts have been made in the past to construct the finite element models for the CFT columns, this modeling may not be appropriate in some cases, especially when using the high-strength concrete or the thin-walled steel tubes that have recently been considered. For this reason, they collected a wide range of experimental tests for the development of a finite element model in the columns under the axial load. They compared the prediction accuracy of the proposed finite element model with the laboratory models. The comparisons showed that the new model for CFT columns is more accurate and more consistent, even when using the high-strength concrete or thin-walled tube. Many researchers have investigated the connection of the beams to the CFT columns because of the weak connection of the columns [8]. Shin et al. (2004) examined the experimental and analytical behavior of CFT column connections to the H beams using the external T-stiffeners. Six samples were tested on the full scale. According to the experimental and analytical results, the proposed strength equations based on the failure mode were proposed to predict the failure modes in the connections reinforced with T-stiffeners, and it was stated that the vertical stiffener for the effective transfer of load from the beam to the column and the horizontal stiffener play a more critical role in increasing the ultimate moment and deformation [9]. Azizi-Namini et al. (2004) considered the moment connections of concrete-filled circular steel tube columns to develop the details of moment connections and the design provisions related to the connection of steel beams to the concrete-filled circular steel tubes. The procedure included the evaluation of the non-elastic response for the details of six types of connection, where the connection as the full passage of the beam from the CFT columns provided the most effective details to achieve a stiff ideal connection [10]. Wu et al. (2005) proposed the bolted connection design to improve the characteristics and performance of the connections, where the stated connections representing the superior seismic resistance in stiffness, strength, ductility, and energy dissipation mechanisms [11]. Han et al. (2008) investigated the behavior of steel beam frame and concrete-filled steel square columns, and the finite element modeling was performed using ABAQUS software to examine the behavior of composite frame under the constant axial load on the columns and the lateral cyclic load on the frame, and the results from the finite element model were confirmed based on the results of the test [12]. Mirghaderi et al. (2010) proposed a plan for connecting the I beam to the box column due to the closure of the column and the difficulty to access inside using a vertical plate passing through the column called the through plate, which can be used for the CFT columns [13]. Hassan et al. (2014) examined the behavior and the configuration performance of the connection between the concrete-filled steel tube columns and the diagonal bracing in the laboratory. This study included 12 subgroups of the connection consisting of a fixed steel tube and a gusset plate connected to the tube end with different details under the half-cycle loading that was tested [14]. Qin et al. (2014) examined the seismic performance of a new connection with the internal diaphragm. The new connection effectively reduces the stress and strain concentration at the end of the beam and moves the plastic hinges to a large extent using the tapered horizontal stiffeners of the beam flanges away from the column surface. The results indicated that this connection can provide the ductility and appropriate energy dissipation capacity for the potential application in the moderate composite moment frames in the seismic areas [15]. Montuori & Piluso (2015) presented a model able to predict the ultimate response of CFT members is also compared with the experimental results [16]. Campione et al. (2016) studied efficiency of stress-strain models of confined concrete with and without steel Jacketing to reproduce experimental results. They examined the reliability of some constitutive laws for concrete confined by steel jacketing [17]. Khanouki et al. (2016) presented a nonlinear finite element model for the beam passing through the circular CFT column with three types of connection failure (beam, column, and joint shear failure) under the uniform loading using the ABAQUS software [18]. The finite element samples in ABAQUS were generated based on the laboratory models of the research program of Elremaily (2001). The results of the finite element showed a good agreement with the laboratory models of Elremaily [19]. Zeinizadeh et al. (2017) in another paper investigated the seismic performance using the intermediate backing plate of the beam connecting the CFT column in a laboratory study. The experimental results showed that the connection has a large confined hysteresis area, optimal ductility and proper energy dissipation. Also, the proposed connection well observes the seismic regulations and the ductile design requirements for the use in the moment frames in the active seismic areas [20]. Vulcu et al. (2016) investigated the high-strength beam-CFT column connections using the external diaphragm, so that the connections consisted of two Reduced Beam Section (RBS) and cover plate connections [21]. Wang et al. (2017) investigated the behavior of the beam connection to the rectangular CFT column using the mixed diaphragm. The mixed diaphragm consists of an internal diaphragm and an external diaphragm, which are combined in the connections of the beam to the rectangular CFT columns to improve the filling characteristics of the concrete in the columns [22]. Hwang & Kwak (2018) proposed reduction factors to determine the ultimate resisting capacity of slender CFT columns without any rigorous nonlinear analysis [23]. Wang et al. (2019) evaluated the seismic behavior of the square concrete-filled steel tube column under cyclic loading. The results showed that the axial compressive load ratio has a significant effect on the hysteresis loops of the square CFT columns [24]. Lin & Zhao (2019) proposed a unified FE model applicable to both small- and large-diameter CFT stub columns. The proposed FE model is used to study the influence of column parameters and size on the behaviors of steel tube and confined concrete in CFT columns [25].
2. ANALYSIS METHOD AND MODELING
The finite element model was developed to evaluate the behavior of two-dimensional (2D) moment-resisting frame with CFT columns considering the reinforcement.
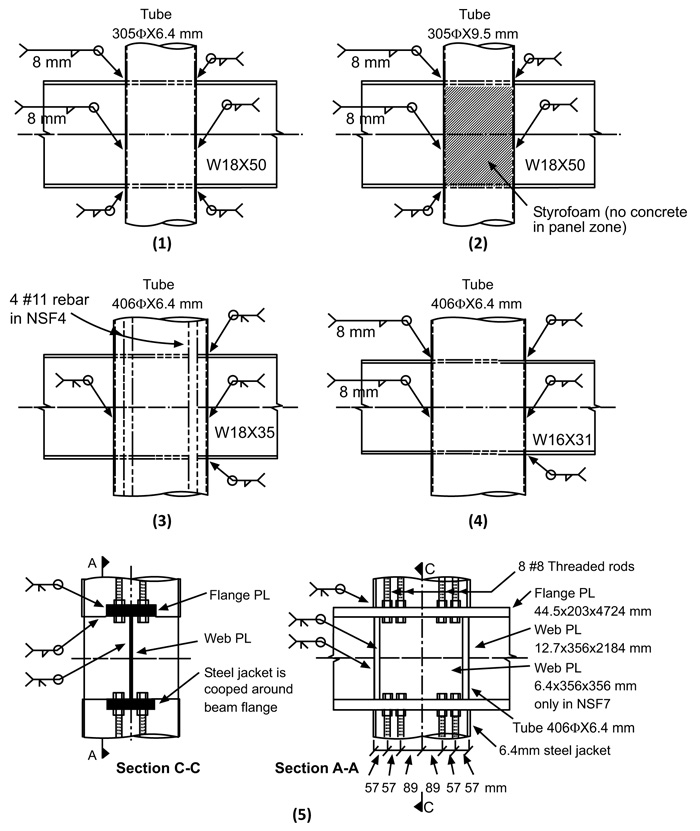
According to previous research, one of the reliable connections for the frames with the CFT column is the full passage of the beam through the CFT columns. According to the laboratory model performed by Elremaily, seven samples were tested on the 2:3 scale. The details of the samples are shown in Fig. (1). The characteristics of the samples were evaluated in three groups: column failure, beam failure, and connection failure. The criterion in this study is the second group, beam failure, which satisfies the regulation codes and indicates that the column should be at least 20% stronger than the beam. According to the descriptions, sample NSF5, which is in the second group, was selected for the verification and modeled with ABAQUS software. It will be used as the criterion for further studies by achieving the results similar to the laboratory ones. Also, the model developed by Arabnejad was used to apply the properties of materials such as steel and concrete in the finite element model. The four-node shell element (S4R) was considered for the steel tubes and beam and the eight-node rigid element (C3D8R) for the concrete core. The concrete plastic damage model was also used for the concrete modeling, and the related parameters such as the dilation angle (ψ) and eccentricity of plastic potential surface (ε) were considered 25° and 0.1, respectively. To model the sample according to the laboratory model, the axial load is applied to the column in the first step, and in the next step, the cyclic loading is applied to both ends of the beam. The surface-to-surface contact between the concrete core and the steel wall is used for the modeling, and the contact parameters of the tangent behavior and the normal behavior are assumed to which the penalty option, applying the friction coefficient of 0.3, and hard contact are applied, respectively. At the points of both ends of the beam and the points of axial load application to the column, the coupling constraint should be applied to constrain the movement of the related surface to the movement of that point. Also, the boundary conditions and the loading amount and method are applied according to the laboratory model.
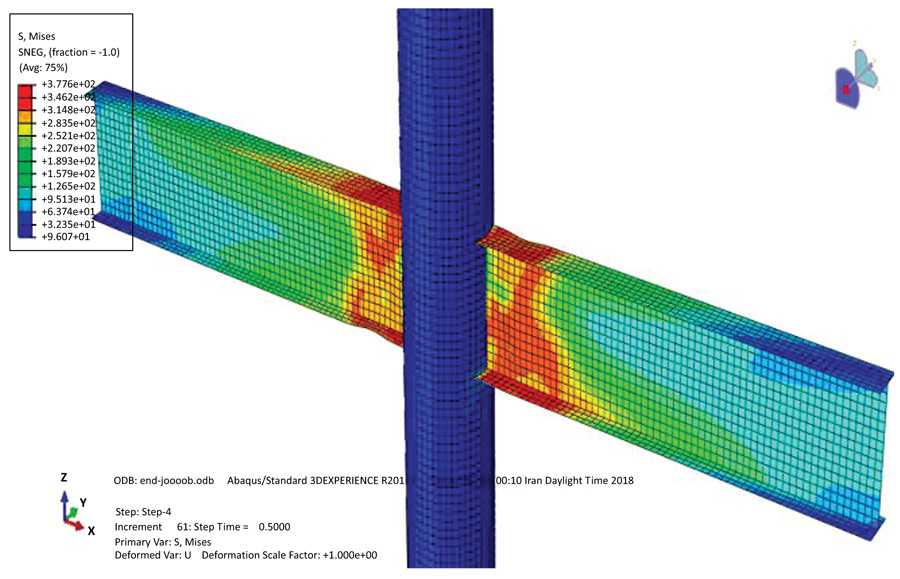
By applying the analysis of the finite element model and the results of the laboratory test, there is a fairly accurate consistency between the two models, and the results confirm the good accuracy of the finite element model and its application to the frame. Fig. (2) shows the Von Mises stress contour on the deformed geometry of the finite element model and the laboratory model for sample NSF5, and the deformation is compared with the laboratory sample. Fig. (3) shows the comparison of the load-displacement diagram for the laboratory model and the finite element model, which indicates the appropriate accuracy in the finite element method.

Also, the absence of damage in the concrete after applying the loading in the laboratory model indicates the proper resistance of the column to the applied load, which is also evident in the finite element model, so that no damage is detected by removing the steel wall and observing the concrete (Fig. 4).

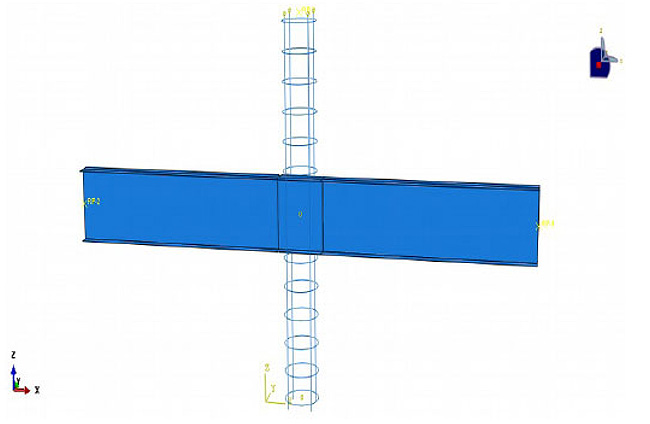
In addition, to further ensure the accuracy of finite element modeling, sample NSF4 was also examined. The only difference between the samples NSF4 and NSF5 in the laboratory modeling was the existence of four rebars (grade-60) in sample NSF4. The laboratory behavior of NSF4 was similar to that of NSF5 in the laboratory model, and the presence of the rebar did not affect the drift-load diagram. This result was similar to the finite element modeling, and by modeling the NSF4 sample in ABAQUS software and comparing it with the NSF5 sample, the drift-load diagram was very close and similar. The rebar was selected with the beam group element of truss type (T3D2). Also, the rebar type AIII was selected with 400-MPa yield stress, 600-MPa failure stress and ultimate strain of 0.14 and other specifications including the Poisson's ratio, etc. were considered as the other steels. Fig. (5) illustrates the rebar layout for NSF4 in the ABAQUS software.
3. DISCUSSION AND RESULTS
Three two-span one-story frames are evaluated with CFT columns, so that frame 1 with the columns without rebar, frame 2 with columns with 1% rebar, and frame 3 with columns with 3% rebar are selected. In these frames, the steel I beam is used which passed through the middle column and placed in the side columns within the column next to the steel wall. The distance between the spans is 6 m, and the beam length is 12.40 m. The height of the columns is also 3.10 m, where the distance from the column top to the edge of the upper flange is 10 cm, and the diameter of the concrete core and steel frame was assumed as 400 and 6.4 mm, respectively. The specifications of beam sections and other material specifications to be used in ABAQUS software are validated.
Regarding the loads applied to the frames, it was assumed that the span perpendicular to the frame was 5 m, the dead load to the roof was 500 Kg/m2 and the live load was 200 Kg/m2, and ultimately, the distributed load to the roof was estimated 0.23 N/mm2, which is uniformly applied to the beam. The lateral loading in the X direction is applied along the beam to the column steel wall. The loading protocol is selected based on JISF 2002 (Japan Iron and Steel Federation). The constant distributed load is applied to the beam and the cyclic lateral load is applied to the frame. The loading and boundary conditions are applied to the structure. The column bases were constrained in all directions, and the beam movement in the y direction was prevented to avoid the lateral torsional buckling.
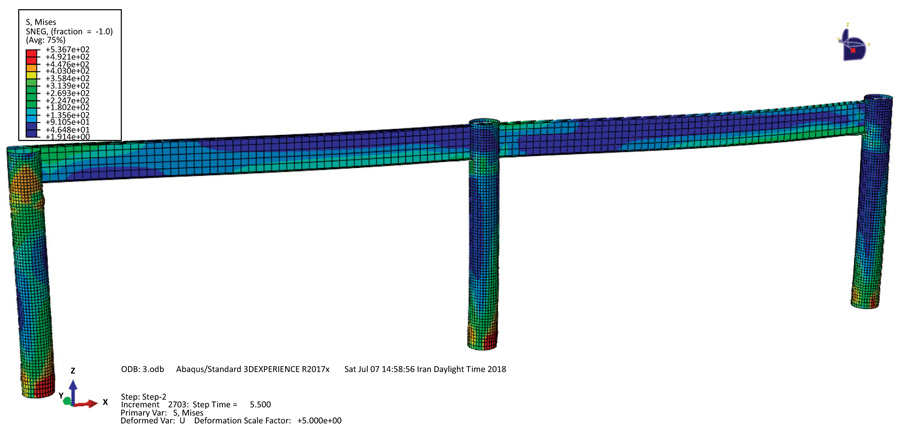
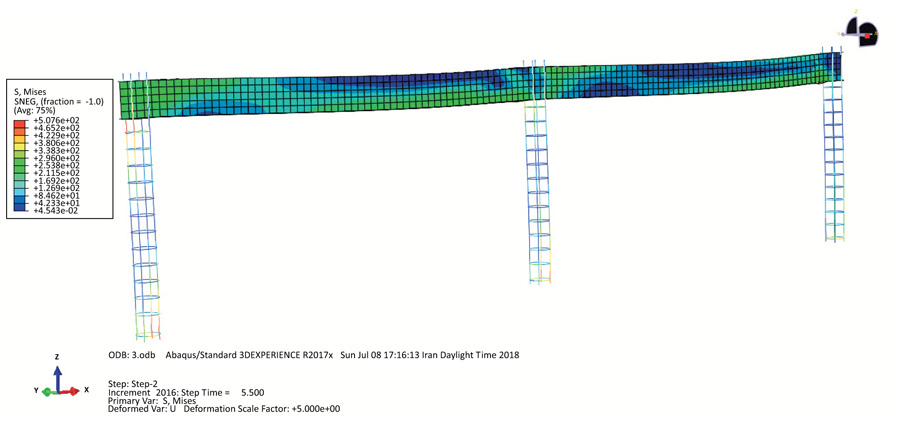
By performing the analysis process in ABAQUS, the deformed view and the Von Mises stress contour of frame 1 without rebar and the removed concrete core for the steel wall are shown in Fig. (6), which indicates the highest stress in the column base in the steel wall.
As mentioned before, 1% rebar inside the concrete core was modeled in frame 2 where four longitudinal rebars ϕ20 were used. The stirrups were placed using the rebar ϕ10@20cm. Also, 3% rebar was used in frame 3 within the concrete core, where four longitudinal rebars ϕ36 were utilized. The stirrups were placed similar to frame 2 using the rebar ϕ10@20cm. Fig. (7) shows the stress contour for the rebar and the steel beam in frame 3.
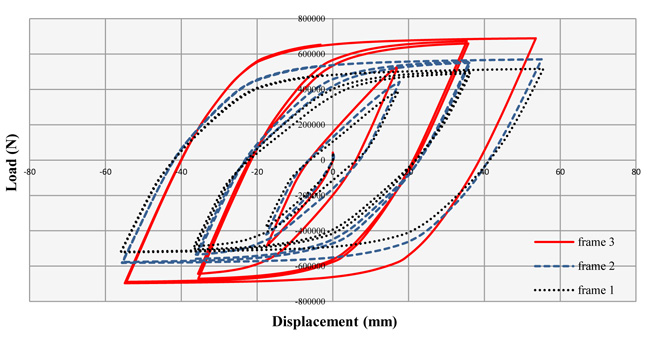
Plotting the hysteresis curve of the frames provides the access to additional information. The area below these curves is in fact the amount of dissipated energy obtained from the loads in the structure. The higher the area, the greater the degree of structural ductility and the higher the potential of structure for the energy dissipation. This is important in seismic areas where the design objective is to improve the structural ductility. Also, the symmetry in the hysteresis curve shows the identical behavior of the structure under the cyclic loads, and the greater the degree of symmetry in the curve, the more uniform the structure behavior under the reciprocating loads. By plotting the hysteresis curve for frame 1 and estimating the area under this curve using the Arean software, 191.5 KJ was obtained. Also, for frame 2, estimating the area under the curve yielded 215.6 KJ. By estimating the area under the curve in frame 3, the value was 251.9 KJ, which shows the amount of energy dissipated by the frame, indicating the greater energy dissipation than the other two frames. Fig. (8) shows the hysteresis curve for three frames in a single image, indicating the difference and the effect of the rebar percentage used in the columns in these curves. According to the descriptions and the hysteresis curves of the three frames, it was evident that the low percentage of rebar has no significant effect on the ductility and energy dissipation of the structure, but the higher percentages of rebar increase the ductility and structure capacity for energy dissipation. As stated before, the area under the hysteresis curve represents the amount of dissipated energy obtained from the loads in the structure. The higher the area, the greater the degree of structural ductility and the higher the structure potential for the energy dissipation. Frame 2 with 1% rebar increased the energy dissipation potential by 11%, and frame 3 with 3% rebar has increased the energy dissipation potential by 24%.
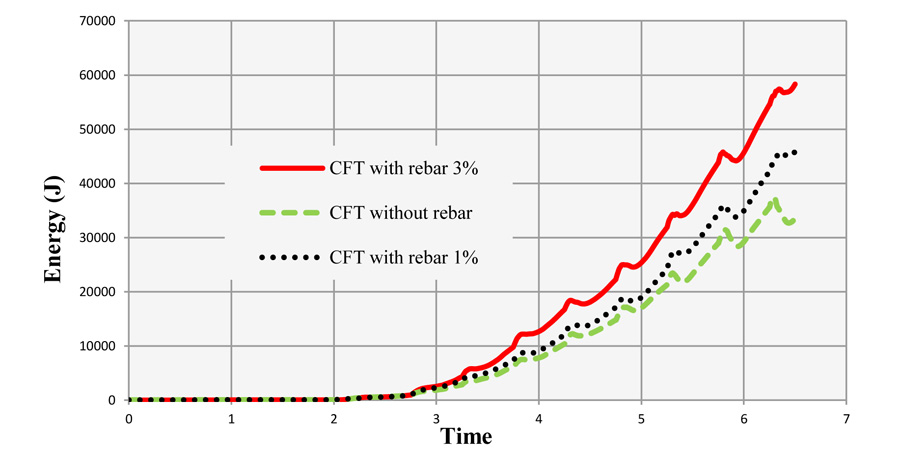
Fig. (9) compares the energy change diagram in three frames. This energy consists of the sum of internal energy, kinetic energy, viscous and frictional dissipation, etc. minus the external work, as expressed in Eq. (1). The diagram indicates the higher energy absorption of the frame with the columns having 3% rebar.
CONCLUSION
The results of the conducted studies can be summarized as follows:
1. Considering the proper consistency of the proposed finite element model with the laboratory results, it is deduced that the proposed model is a suitable method to be used in future research.
2. The hysteresis curves investigated for the three frames and the estimation of the area under the curves suggest the superiority of frame 3 with the use of 3% rebar inside the concrete core, so that in frame 1 without using the rebar, the area under the curve was 191.5; in frame 2 with 1% rebar, the area under the curve was 215.6; and in frame 3 with 3% rebar within the concrete core, the area under the curve was estimated 251.9, which indicates the 11% increase in the ductility and energy dissipation of frame 2 relative to frame 1 and 24% increase in frame 3 relative to frame 1.
3. According to the results, the very low percentages of rebar (e.g., less than 1%) in CFT columns do not significantly change the hysteresis curve, and the area under this curve is not considerably increased, and as a result, it does not greatly influence the ductility and energy dissipation of the frame.
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
Not Applicable.
FUNDING
None.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.


