All published articles of this journal are available on ScienceDirect.
The Effect of slit-friction hybrid damper on the Performance of Dual System
Abstract
Aims:
The aim of the present paper is to evaluate the behavior of slit friction hybrid dampers (SFHD) on steel structures. Therefore, the behavior moment resisting steel frames of structures in original stats and structures equipped with hybrid damper with two different types of behavior was analyzed and evaluated.
Background:
The recent study evaluated the combined effect of shear-friction dampers and slit dampers with measurements of non-uniform strips in seismic protection for different levels of energy. The recent study was carried out about hybrid dampers, consisting of friction and split dampers in response to small and large earthquakes. Previous results have shown the ability of inactive hybrid systems in improving the reaction of structures to traditional lateral-systems. Kim and Shin showed that structures consisted of hybrid dampers needed less repair cost and time.
Methods:
Pushover and time history were carried out in original structures and structures equipped with dampers, in 5 and 10 stories structures.
Results:
Analysis about the probability of collapse showed about 30% and 84%.
Conclusion:
According to the result, by adding the SFHD, increased stiffness by 17% in retrofitted structures, such as drift and displacement of roof decreases by 27% and 20% in push over analysis, respectively. Also, displacement in time history analysis up to 55% reduces in average. Also, the results of the IDA show that adding the SFHD to structures significantly increases by 55% of the spectral acceleration capacity in structures.
1. INTRODUCTION
Recently, steel dampers and friction dampers have been produced by two of the most widely energy dissipating equipment that is used in structures. Adding Damping and Adding Stiffness damper (ADAS) Xia and Hanson i [1], Resistant buckling braces Park et al. [2] and Slit dampers Chan and Albermani [3] are examples of the energy dissipation devices. Hu evaluated the effect of slit dampers on shape memory alloy [4]. Kim et al. estimated the effect of Rotational Friction Damper on the increase of seismic capacity and collapse resistance in 2011 [5]. Patel and Jangid studied the dynamic responses of close structures that were fastened to each other with a friction damper [6]. Samani et al. have done experimental and numerical studies on the hysteretic behavior of friction dampers. They illustrated that wear and heat decrease the slippage load and as a result, reduce the energy dissipation of the damper [7]. Kaur et al. compared the seismic performance of the moment-resisting frames equipped with a friction damper with moment frames and braced moment frames [8]. Bagheri et al. assessed the seismic performance of structures with U-shaped dampers and the seismic performance of the frames including U shaped dampers compared to the frames equipped with friction damper [9]. Pall [10], Mualla and Belev evaluated the friction dampers which have been used in various shapes [11]. Recently, Lee et al. evaluated friction dampers that caused energy dissipating through producing friction between materials with low steel and milled steel. Some researchers have evaluated the energy dissipation devices and passive dampers, which are widely used in seismic retrofitted of structures [12]. For example, Tsaei et al. [13], Chen et al. [14] and Uetani et al. [15] evaluated the combinational devices, displacement-dependent and velocity-dependent to reduce the seismic of behavior structures and minimize errors of dampers that were used separately. Using the method of adding the dampers in the shear wall, Marko et al. studied the effect of hybrid friction-viscoelastic dampers and evaluated seismic responses of the structures when these dampers were placed in the structure [16]. Marshall and Charney [17] studied hybrid systems which consisted of a combination of resistant buckling dampers and fluid viscous devices, and evaluated the seismic responses of the structures. Recently, studies have evaluated the optimal design of hybrid dampers on the seismic responses of structures which consisted of a combination of resistant buckling braces and fluid viscous tools. Supradip and Rama [18] have studied the effect of multiple tuned liquid damper (MTLD) and single tuned liquid damper (STLD), on the reduction of the structural response under dynamic loading. They illustrated that MTLD and STLD have a significant effect on the reduction of structural response. Pisal and Jangid [19] investigated the effectiveness of tuned mass friction damper (TMFD) and different tuned mass friction parameters, in reducing the dynamic responses of structures. They showed that structures equipped with (TMFD) have reduced structural response compared to original structures. Optimum design methods for hybrid or multiple dampers were developed by Murakami et al. [20] and Lee and Kim [21]. They have evaluated the effect of the combining devices of slit damper and friction rotational damper in reducing the seismic of structures in small and large earthquakes. In the study by Heidari et al. [22], the displacement and acceleration decreased after applying a hybrid control system in structures that consisted of the active tuned mass damper. Lee et al. [23] evaluated the combined effect of shear-friction dampers and slit dampers with measurements of non-uniform strips in seismic protection for different levels of energy. Lee et al. [24] carried out a study on hybrid dampers, consisting of friction and split dampers in response to small and large earthquakes. Previous results have shown the ability of inactive hybrid systems in improving the reaction of structures to traditional lateral-systems. Kim and Shin showed that structures consisted of hybrid dampers needed less repair cost and time [25]. The purpose of the present paper is to evaluate the behavior of slit friction hybrid dampers (SFHD) on steel structures. Therefore, the behavior of Dual system in original states and structures equipped with hybrid damper with two different types of behavior was analyzed and evaluated.
2. METHODOLOGY
2.1. Slit-Friction Hybrid Damper Description
Slit friction hybrid damper (SFHD) consisting of a friction and slit damper which were/have been installed in alongside. The yield strength and stiffness in these dampers were composed of a combination of yield strength and friction stiffness and slit dampers which were calculated according to equations 1 and 2 [24, 25].
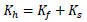 |
(1) |
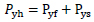 |
(2) |
Where, Kh was the stiffness of hybrid damper, Kf was the stiffness of friction damper and KS was the stiffness of the slit damper. The term Pyh was the yield strength of a SFHD and Pyf was the yield strength of a friction damper. The Pys was the yield strength of a slit damper. Table 1, shows properties of the friction damper, the slit damper and the hybrid damper from experiments and analytical models, which are used in this study.
In SFHD, the friction dampers resisted against weak earthquakes and strong winds and slit damper resisted against strong earthquakes. These dampers were essentially displacement-dependent devices which dissipated seismic energy by producing steel strips and slipping friction plates in a friction damper. The sliding of the friction plates occurs in small displacements caused by weak earthquakes and strong winds. In that case, the slit damper remains in a flexible state and is activated only in large earthquakes. Therefore, the slit damper led to energy dissipation through the shear and yield deformations [24].
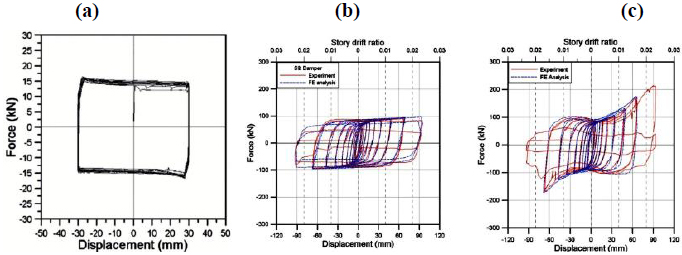
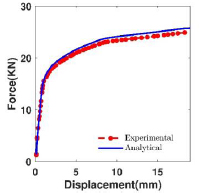
In this damper, two types of dampers, namely friction damper and slit damper, were connected in parallel. The width and height of the plate, considering that these two types of dampers were connected, were 500 and 700 mm, respectively. On this plate, there were 9 stripes with b as width, t as thickness and L as length, which were 20, 15 and 200 mm, respectively. Using bolted steel bars and nuts, a friction circle plate was attached to the slit plate with a diameter of 100 mm. A deep hollow with a depth of 1 mm was created on either side of the plan surface of the slit damper and the steel bar in order to prevent the lateral movement of the slit plates and radial stretching of the plates due to the strained force produced by the bolt and nut. Due to the existence of high-tension bolt and nut on the surface of the friction plate, the frictional force of the plates was distributed between the upper bolt and nut and the steel bar. Pre-stressing bolt and nut were used to produce a compressive force on friction plates with a tensile strength of 2 kN / mm2 and a diameter of 20 mm Lee et al. [24]. There were Teflon washers at the end of the steel bar, and the bolts and nuts were loosely closed in order to reduce frictional force. The coefficient of the friction between the plates was considered to be 0.5 as shown in (Fig. 1). Hysteresis curves of the friction, slit and hybrid dampers are shown in (Fig. 2). In these figures, experimental results and finite element analyses are very close.
2.2. Design, Modeling and Assumptions
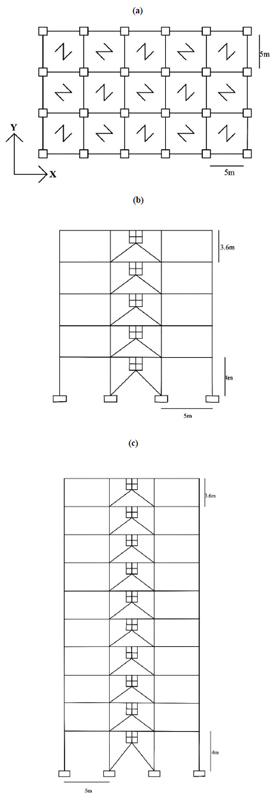
The applied structural models in this research were considered as the moment-resisting steel frame with the intermediate ductility with the number of 5 and 10 stories. These structures had 5 bays of 5 meters in the X direction and 3 bays of 5 meters in the Y direction and the dampers were set between the upper end of the braces and the lower part of the beam in the frame. The height of the first floor was 4 meters and the other floors 3.6 meters. The bearings were assumed to be fixed supports. The sections that used for columns and braces were BOX and they were IPE for beams. The geometry of the used frames and plan of these structures are shown in Fig. 3, (Tables 2 and 3). In the design of frames, the dead load, live load, roof live load, snow load and partition load were equal to 600kg/m2, 240kg/m2, 96kg/m2, 196kg/m2 and 126kg/m2, respectively. Seismic loading for primary analysis and design was based on the ASCE07-16 code. The loading bearing of the roof was a steel decking type. The critical damping ratio in the structure was by 5% and soil type was D based on ASCE07-16 [26]. The construction site was located in Montana with seismic accelerations Ss =1.712g, S1 = 0.5g. The steel stress-strain and moment-curvature relationships were assumed to be bilinear, with a strain hardening ratio of 3% Sayani et al. [27] and Parvini et al. [28]. In the structures equipped with hybrid damper, the design of the members of the frame was in such a way that it remained in an elastic region while only the damper entered the non-linear region. The behavior of the hybrid damper that could resist in axial and shear forces was a Raber Isolator type [24]. In order to evaluate the behavior of the frames without damper and frames equipped with a damper during an earthquake, nonlinear static and nonlinear time histories analysis were used by ETABS2016 software [29] and SiesmoStruct 2016 software [30]. Regarding this, seven pairs of far field acceleration records were used according to the FEMA-P695 [3], as shown in Table 4.
2.3. Verification of Analytical Models
2.3.1. Slit Damper
Chan and Albermani in the year 2008, carried out experimental and analytic studies on the slit damper [3]. They obtained the capacity curve for a steel frame equipped with slit damper. Numerical analyses performed here verify in detail the experimental results and our results recover their experimental results, showing that the modeling details verify those experimental results in (Fig. 4).
2.3.2. Friction Damper
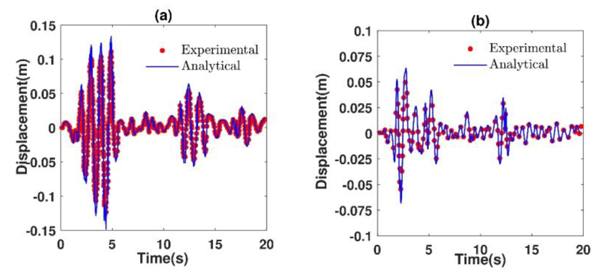
Mualla and Belev in the year 2008 have conducted experimental and analytic studies on friction damper [11]. They found the response of the steel frame equipped with slit damper under El Centro ground motion. Numerical analyses were done and our results recover their experimental results as shown in (Fig. 5).
3. NUMERICAL RESULTS
3.1. Pushover Analysis Outcome
The development of the nonlinear static analysis also called the pushover analysis, originated as a simplified performance evaluation tool. Pushover analysis uses a height-wise lateral load distribution pattern considering the contribution of higher modes as in the modal pushover analysis to calculate the inelastic seismic demands of the structure Bhandari et al. [32]. Static pushover analysis provides advantageous data on the lateral strength and ductility of structures Shokrabadi [33].
3.1.1. Capacity Curve
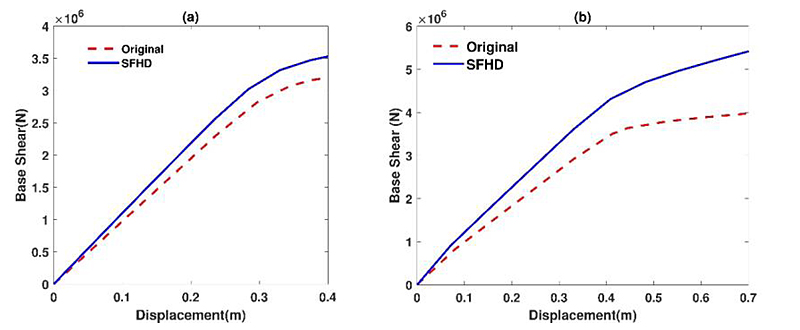
The capacity curve is base shear in terms of the lateral displacement of the structural curve [34]. To obtain the capacity curve, pushover analysis is done. The results of the analysis, as shown in (Fig. 6), display that according to the force-displacement curve, the increased stiffness in the 5 and 10 stories structures equipped with SFHD were increased by 10% and 25% respectively, compared to the original structures.
3.1.2. Drift
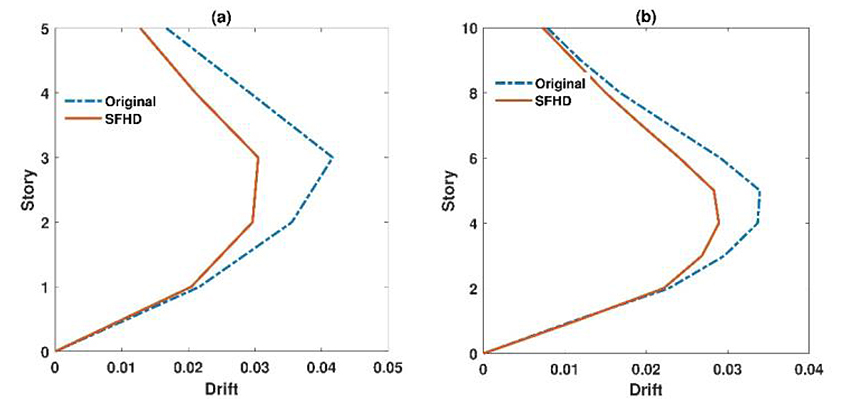
According to the results presented in (Fig. 7) drift in retrofitted 5 and 10 story structures was decreased by 33% and 22% respectively, compared to original structures which showed that SFHD plays an important role in increasing the capacity of energy dissipation.
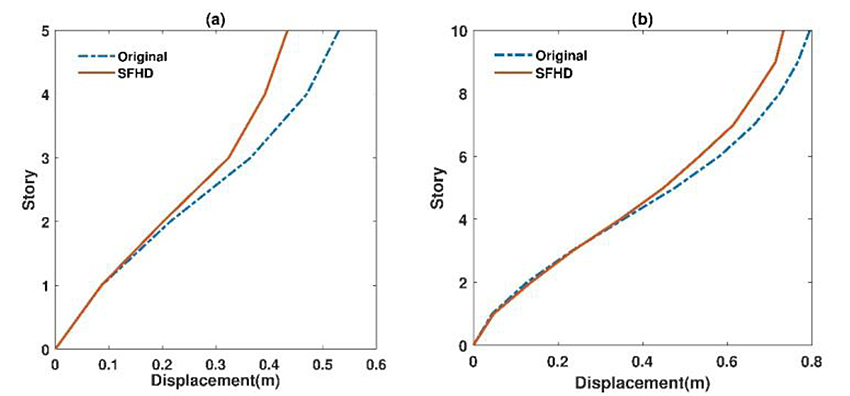
3.1.3. Roof Displacement
According to the diagrams presented in (Fig. 8) the maximum displacement of roofs in the 5 and 10 structures with SFHD has decreased by 27% and 13% compared to the structures without damper. The reduction of the maximum displacement of the roof led to the reduction in the plastic rotation and thus reduced structural and non-structural damage.
4. TIME HISTORY ANALYSIS
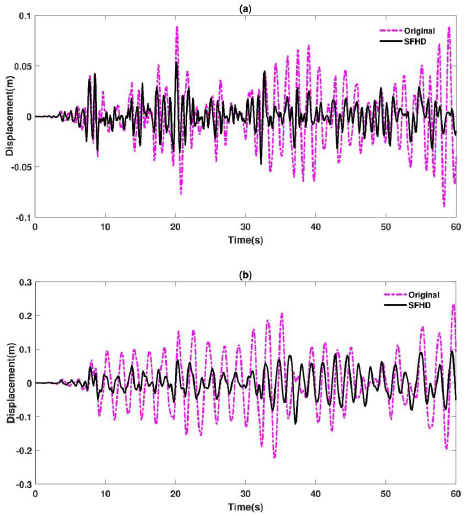
Nonlinear dynamic analyses were conducted on the 5 and 10 stories under 7 pairs of a far filed ground motions. The results of time history analysis showed that displacement of the 5 and 10 stories structures under Imperial Valley earthquake in the structures including SFHD was reduced by 45% and 65% compared to the original structures. This showed that the energy dissipation capacity in retrofitted structures has increased due to non-elastic behaviors and as presented in (Fig. 9) it could be stated that SFHD had a significant role in reducing the lateral displacements compared to the original state.
5. INCREMENTAL DYNAMIC ANALYSIS AND COLLAPSE ASSESSMENT RESULTS
Incremental dynamic analysis (IDA) is a significant technique to evaluate the collapse of structures using a sequence of nonlinear dynamic analyses under suitably multiplied scaled ground motion records Parvini et al. [35]. The IDA makes use of multiple response history analyses for a given ground motion record of increasing intensity until collapse takes place. The collapse capacity for structures is defined based on an inter-story drift ratio limit up to 10% Baker and cornell [36]. The “hunt and fill” algorithm can be used for this procedure Vamvatsikos and Cornell [37].

| Theoretical Value Experimental Results | ||
|---|---|---|
| (δy friction, Py friction) | (0mm,37.5 kN) | (0.8mm, 37.8 kN) |
| (δy slit, Py slit) | (1.6 mm, 48.75 KN) | (3.0mm, 46.7KN) |
| (δmax, Pmax) | (65.0 mm, 124.8 KN) | (63.38 mm, 120.0 KN) |
| KSE, Elastic stiffness of slit dampers | 30.66 KN/mm | 15.57 kN/mm |
| KSp, Post-yield stiffness of slit dampers | 0.61 kN/mm | 0.60 KN/mm |
| Applied sections | |||
|---|---|---|---|
| Number of the stories | Columns | Beams | Braces |
| First story | BOX:250*250*20 | IPE330 | BOX:120*120*10 |
| Second story | BOX:250*250*20 | IPE330 | BOX:120*120*10 |
| Third story | BOX:200*200*20 | IPE300 | BOX:120*120*10 |
| Fourth story | BOX:200*200*20 | IPE300 | BOX:120*120*10 |
| Fifth story | BOX:180*180*20 | IPE240 | BOX:120*120*10 |
| Applied sections | |||
|---|---|---|---|
| Number of the stories | Columns | Beams | Braces |
| First story | BOX:350*350*20 | IPE360 | BOX:180*180*10 |
| Second story | BOX:350*350*20 | IPE360 | BOX:180*180*10 |
| Third story | BOX:350*350*20 | IPE360 | BOX:180*180*10 |
| Fourth story | BOX:350*350*20 | IPE360 | BOX:180*180*10 |
| Fifth story | BOX:330*330*20 | IPE330 | BOX:180*180*10 |
| Sixth story | BOX:330*330*20 | IPE330 | BOX:180*180*10 |
| Seventh story | BOX:330*330*20 | IPE300 | BOX:180*180*10 |
| Eighth story | BOX:330*330*20 | IPE300 | BOX:180*180*10 |
| Ninth story | BOX:300*300*20 | IPE270 | BOX:180*180*10 |
| Tenth story | BOX:300*300*20 | IPE270 | BOX:180*180*10 |
| PEER-NGA Records Information | ||||||
|---|---|---|---|---|---|---|
| Recorded | Montions | |||||
| ID NO. |
Record Seq.No. |
Lowest Freq(HZ) |
Component 1 | Component 2 | PGAmax (g) |
PGVmax (cm/s) |
| 1 | 169 | 0.06 | IMPVALL/H-DLT262 | IMPVALL/H-DLT352 | 0.35 | 33 |
| 2 | 174 | 0.25 | IMPVALL/H-E11140 | IMPVALL/H-E11230 | 0.38 | 42 |
| 3 | 752 | 0.13 | LOMAP/CAP000 | LOMAP/CAP090 | 0.53 | 35 |
| 4 | 767 | 0.13 | LOMAP/G03000 | LOMAP/G03090 | 0.56 | 45 |
| 5 | 848 | 0.13 | LANDERS/CLW-LN | LANDERS/CLW-TR | 0.42 | 42 |
| 6 | 900 | 0.07 | LANDERS/CLW-YER270 | LANDERS/CLW-YER360 | 0.24 | 52 |
| 7 | 953 | 0.25 | NORTHR/MUL009 | NORTHR/MUL279 | 0.52 | 63 |
Asgarian et al, incremental dynamic analysis (IDA) was applied in Tehran telecommunication tower. They used three different finite element models. The results exhibit that there is an acceptable consequence between Two-dimensional and Three-dimensional models in linear and nonlinear analysis [38]. Hariri et al, studies were done on seismic stability of a high-rise concrete tower under endurance time analysis (ETA). For this purpose, a Two-dimensional fiber element model of the tower was used and analyzed. The result shows that the peak ground velocity and spectral acceleration are very suitable measuring parameters for comparing the (IDA) with (ETA) technique [39].
5.1. Incremental Dynamic Analysis
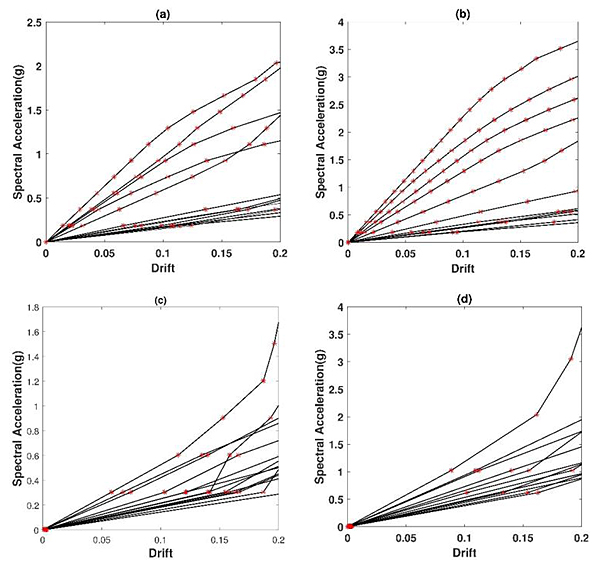
In order to obtain the seismic fragility, we applied the IDA using seven pairs of far field acceleration records by FEMA-p695. This analysis was carried out for structures of 5 and 10 stories without dampers and with SFHD. The results obtained from the analysis showed, higher spectral accelerations and a drift of the stories occurred in structures equipped with SFHD in comparison with the original state, and as observed in (Fig. 10) it could be explained that by adding SFHD to structures the amount of spectral accelerations capacity increased by 50% and 62%.
5.2. Probability of collapse
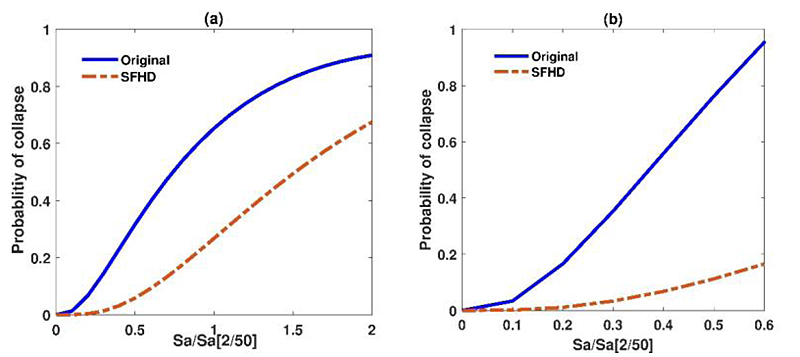
By a maximum credible earthquake, after analyzing the IDA, it was possible to obtain the probability of collapse for original structures and structures equipped with SFHD. The probability of collapse curves followed the Log normal distribution. According to the results presented in (Fig. 11) it could be observed that the probability of collapse in structures equipped with SFHD was reduced by 30% and 84% compared to the original structures.
CONCLUSION
This study has focused on the effect of a slit friction hybrid damper (SFHD) on the moment resisting steel frame. For this purpose, pushover and time history was carried out on original structures and structures equipped with dampers in 5 and 10 stories structures. The results of the pushover analysis showed that the increased stiffness by 10% & 25% in 5 and 10 stories structures equipped with SFHD and in structures with SFHD compared to the original structures, the drift and the displacement of roof was reduced by 33% & 22% and 27% & 13%, respectively. The results of the time history analysis showed that the displacement of the structure was reduced by up to 45% & 65% in structures equipped with SFHD. Also, an incremental dynamic analysis showed that structures strengthened with SFHD had a significant spectral acceleration capacity of approximately 50% & 62% compared to the original structures. Analysis of the probability of collapse showed about 30% & 84% decrease in the probability of collapse in reinforced structures compared to the original state.
CONSENT FOR PUBLICATION
Not applicable.
FUNDING
None.
CONFLICT OF INTEREST
The authors declares no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.


