All published articles of this journal are available on ScienceDirect.
A New Approach for the Evaluation of Structural Failure by Credibility Distribution
Abstract
Aim:
To devise an effective structural failure analysis approach under uncertainty.
Background:
In reliability evaluation, plenty of factors are uncertain, or sometimes, spontaneously represented via linguistic expressions, and as a consequence, the traditionalist appraisal methods cannot capably handle the ambiguity and vagueness that occurs in reliability assessment components. Subsequently, this leads to the problem of tremendous computationally multifaceted and scanty correctness.
Objective:
To overcome the limitations and to develop efficiency as well as accuracy in structural failure evaluation techniques, an attempt has been made to devise a novel structural reliability assessment method via credibility distribution.
Methods:
To get rid of the problems of massive computationally difficult and inadequate precision, an algorithm has been devised using credibility sampling. To exhibit the novelty, validity, and applicability of the present approach, some structural failure assessment problems are solved along with a comparison with the existing approach.
Results:
The proposed method was verified by four examples and applied in structural analysis. It was observed that the present approach is technically sound and efficient; it can overcome all the drawbacks of the existing approach. Moreover, the approach can be executed in any uncertain situation.
Conclusion:
After evaluation of failure assessment, it is experienced that the increase in the number of simulations leads to better precision. Furthermore, it is encountered that when hybridization problems i.e., representation of imprecise components in the problem of structural failure, are both fuzzy and probabilistic nature, then the failure assessment is attained to be maximum.
1. INTRODUCTION
At present, reliability analysis may be the most interesting research topic among the researchers, due to the occurrence of persuading imprecision in the reliability assessment procedures have become profound [1].
Most frequently, the foremost classical and prevailing tool, i.e. probability theory, is explored to affect uncertain variables in reliability analysis. Furthermore, probability theory is exploited to gauge structural reliability analysis through the probability of failure [2-5].
The application of FST in structural reliability is found to be more convenient rather than the probabilistic models [6-10]. By using fuzzy random variables, some attempts [11-13] were made to resolve the structural reliability problems, during which the fuzzy numbers represented imprecise parameters of the probability distributions of the variate.
Some non-probabilistic reliability analysis methods like interval analysis method14, the convex model method [14], possibility theory method [15], and Dempster-Shafer theory based method [16, 17], are also used.
On the other hand, in real-world conditions, it is observed that some input components of structural analysis are represented by Probability Density Functions (PDFs) and a few others are represented by FST. In such situations, hybrid methods are devised to review reliability assessment [18, 19].
From these reassess, it is often advocated that structural reliability supported PDFs, FST, and hybrid methods usually produce insufficient and inaccurate solutions [20]. More imprecise results are found in DST based structural reliability analysis [21].
The deficiencies of all the available approaches motivate us for an attempt to devise a completely unique structural reliability computation method via credibility distribution. Furthermore, a comparative analysis with the prevailing approach and therefore, the present approach, has been presented in conjunction with solutions to some structural problems under this setting.
2. METHODS TO MODEL UNCERTAINTY
In this section, some important concepts and definitions of FST and credibility theory are presented.
Definition: A Fuzzy Set (FS) M on the universal set U can be described by its Membership Function (MF) [22]:
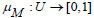 |
Where, μM(α) at α shows the degree of membership of α in M.
Definition: A Triangular Fuzzy Number (TFN) A is denoted as a triplet A = [p1, p2, p3] whose MF is defined as (equation 1):
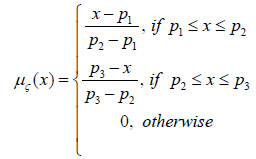 |
(1) |
Definition: A Gaussian Fuzzy Number (GFN) Gauss([p1, p2]), where the MF is defined as (equation 2):
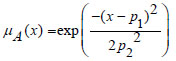 |
(2) |
Where, p1 represents the center of the MF and p2 represents the width of the MF.
Definition: A Cauchy Fuzzy Number (CFN) Cauchy([m, n]) whose MF is defined as (equation 3)
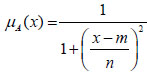 |
(3) |
Where, m represents the center of MF and n determines the width of the Membership Function.
The basic idea of credibility theory can be obtained in literature [22].
Suppose ζ = (p1, p2, p3) is a fuzzy variable with (p1 < p2 < p3); where MF (equation 4) is
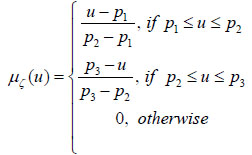 |
(4) |
Then the Credibility Distribution Function (CDF) ζ (equation 5) is:
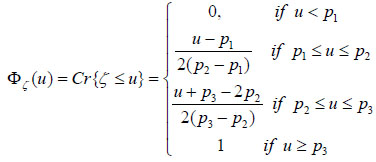 |
(5) |
Similarly, for the GFN A = Gauss([p1, p2]), the CDF (equation 6) is:
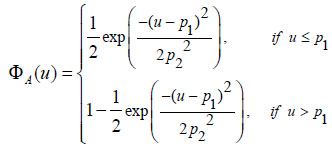 |
(6) |
Also, the for the CFN Cauchy([m, n]), the CDF (equation 7) is:
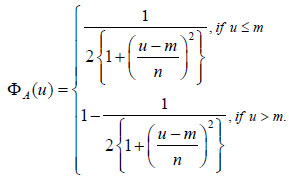 |
(7) |
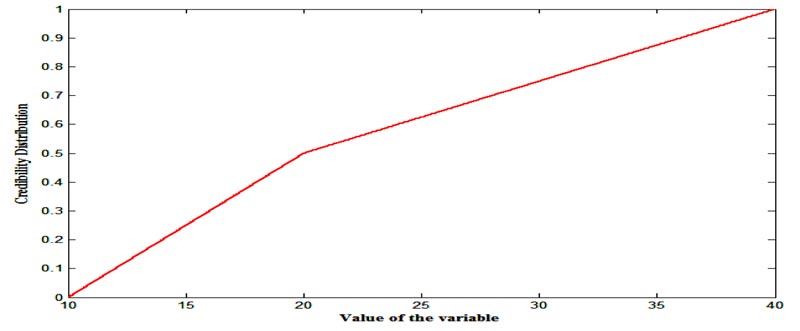
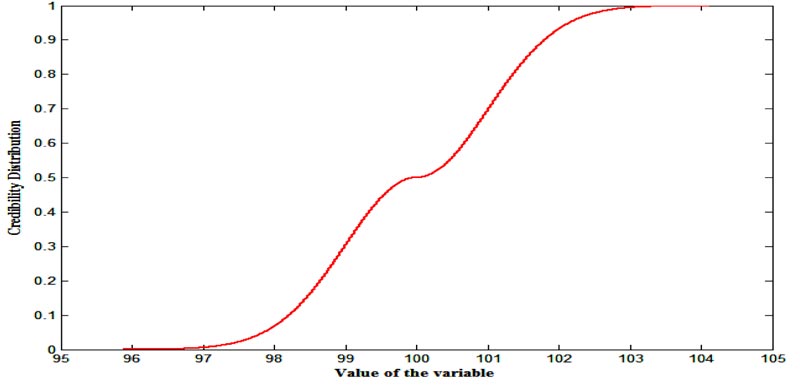
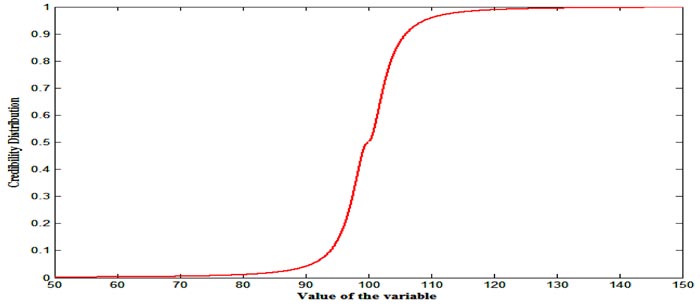
Then, for the CDFs of the fuzzy variables X = [10, 20,40], Y = Gauss [20, 1] and Z = Cauchy[100,3] are depicted in Figs. (1-3), respectively.
3. METHODOLOGY
In this section, a completely unique structural reliability assessment technique is presented.
Suppose the reference function is
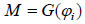 |
(8) |
Where, φi represents fuzzy variables of different types.
Step-I: Convert all FVs of equation (8) into CDs.
Step-II: Generate wl(i is the total number of fuzzy variables or credibility distributions) number of uniformly distributed random numbers from [0,1].
Step-III: Generate random numbers rl(each random number for each credibility distribution) by transforming wl using the inverse transformation method.
Step-IV: Calculate M = G(φi).
Step-V: Failure takes place if M ≤ 0, i.e., failure domain is M* = [-∞, 0].
Then the failure of the structure can be evaluated
• Case-I: For M ϵ M*, Cred* = 1.
• Case-II For M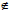 M*, Cred* = 0
M*, Cred* = 0
Step-VI: Repeat the process for N times.
Step-VII: Structural failure = 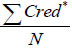 .
.
Step-VIII: Plot CDF of M.
In some situations, representation of the components of structural reliability assessments are fuzzy variables alongside probability distributions. In such situations, structural failure is often calculated that needs to transform all FVs to CDs first, while probability distributions remain equivalent. Then, inverse transformation for credibility distributions and Monte-Carlo simulation for the PDFs are performed, and then all the steps mentioned above should be followed.
4. NUMERICAL ILLUSTRATIONS AND COMPARATIVE ANALYSIS
During this section, the reliability assessment of a beam/bar and heat transfer problem concerning the credibility of the melting of the slab is calculated. Furthermore, a comparison is also made with the prevailing approach [23]. In a study [23], a reliability measurement technique based on the area of resultant fuzzy variable concept is encountered, where failure reliability was evaluated because the area of the negative part upon the entire area of the resultant fuzzy number is presented. During this technique, it had been assumed that if the resultant fuzzy variable falls below 0, then reliability is taken into account to be 0 and if the resultant fuzzy variable does not contain negative values then the designe is assumed to be extremely secure, and for this case, reliability value is 1.
Example 1: Suppose a bar with capacity R and load S (Fig. 4), the limit state function (equation 9) is
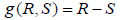 |
(9) |
Where, R and S both are uncertain variables whose representations are triangular fuzzy (numbers) variables such that R = [30,45,55] and S = [25,35,65]. It is needed to gauge the reliability assessment or failure assessment of the bar.

Here, it is required first to convert FVs R and S into CDs ΦR (equation 10) and ΦS (equation 11) which are given as,
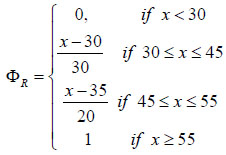 |
(10) |
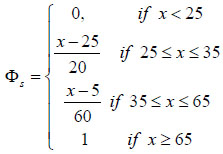 |
(11) |
Then, it is required to generate two random numbers (uniform) from [0,1], say r1 and s1 for the two credibility distributions. Using credibility sampling, two values Φ-1R(r1) and Φ-1S(s1) for ΦR and ΦS respectively can be obtained. Then, it is needed to evaluate:
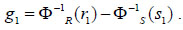 |
If, g1 > 0 then credibility value (Cr1) = 0 and if g1 < 0 then credibility value (Cr1) = 1.
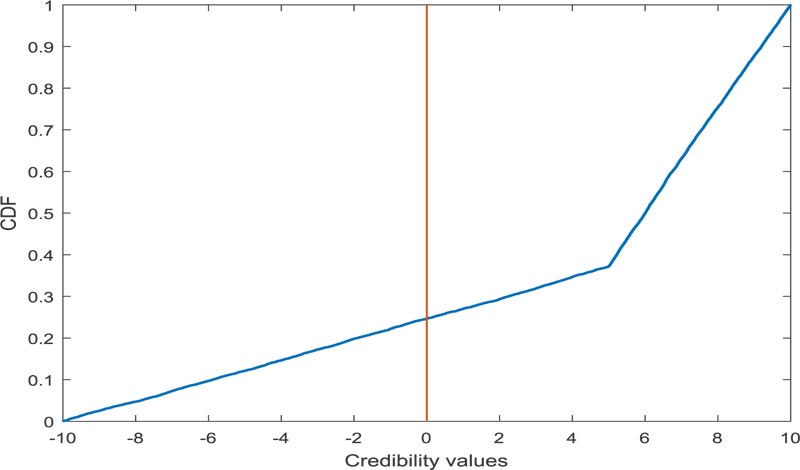
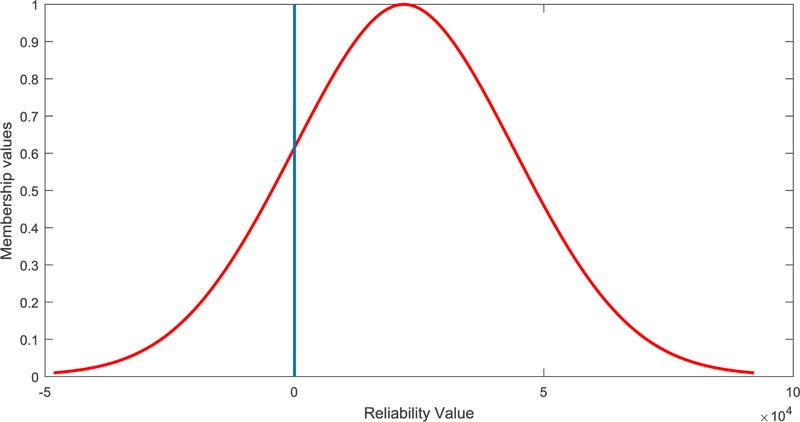
Proceeding in this way for N number of times for different random numbers, the failure assessment will be 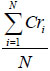 and is presented in Table 1. Furthermore, CDF of the resultant M is presented in Fig. (5).
and is presented in Table 1. Furthermore, CDF of the resultant M is presented in Fig. (5).
| Sl.No | Failure Assessment | Simulation Number (N) |
|---|---|---|
| 1 | 0.2520 | 1000 |
| 2 | 0.2512 | 5000 |
| 3 | 0.2500 | 10000 |
| 4 | 0.2499 | 100000 |
| 5 | 0.2498 | 1000000 |
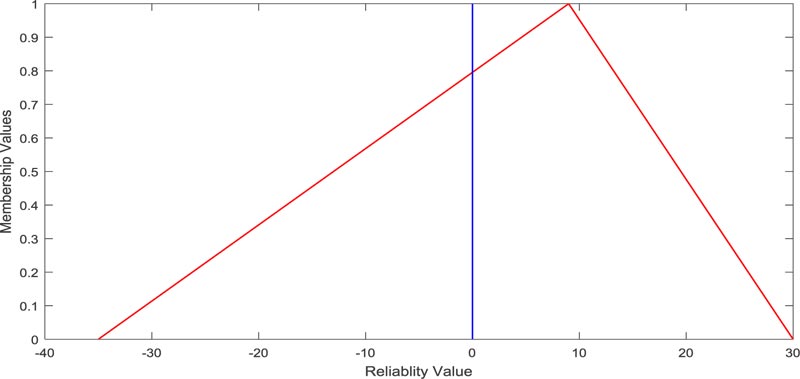
Using the existing approach [23], the failure assessment is obtained as the fuzzy number [-35,9,30], whose graphical representation is depicted in Fig. (6). The area-based failure assessment value is 0.5385.
Example 2: Suppose a beam (Fig.7) with length L = 1300mm, beam height h = 8mm and the force density f = 78.5x10-5kN/mm3 with imprecise load w = Cauchy (400,1.5) kN, breadth b = Gauss (40,15) mm and bending moment Mo = [2x105, 2.05x105, 2.1x105] kN-mm.
Suppose the reference function (equation 12) is:
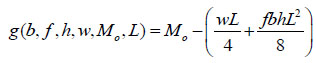 |
(12) |
Here also, it is needed to gauge the failure assessment of the beam.
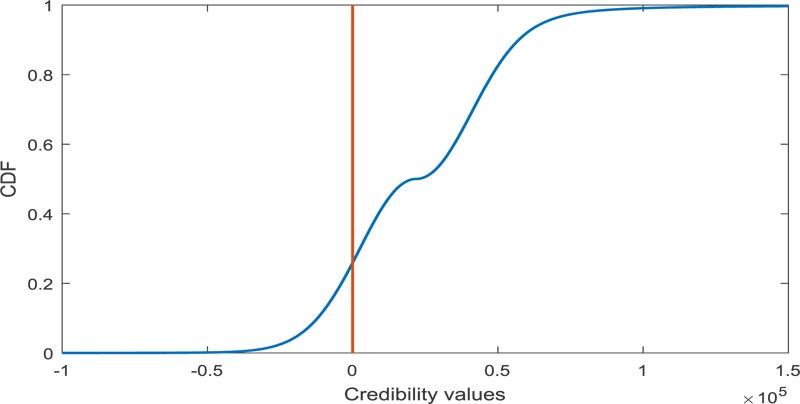
In this problem, FVs w, b and Mo are to be converted into CDs first, and accordingly, failure assessment is calculated using the proposed technique, which is presented in Table 2, and the corresponding CD is depicted in Fig. (8).

| Sl.No | Failure Assessment | Simulation Number (N) |
|---|---|---|
| 1 | 0.2530 | 1000 |
| 2 | 0.2442 | 5000 |
| 3 | 0.2422 | 10000 |
| 4 | 0.2417 | 100000 |
| 5 | 0.2411 | 1000000 |
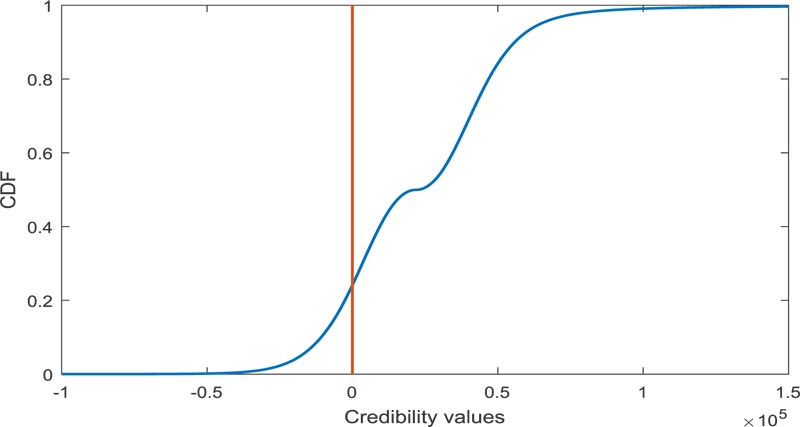
The evaluation of failure assessment using the existing approach [23], in this case, is not eased as the resultant fuzzy number is not of linear type. The resultant fuzzy number is obtained to be [-4.826x104, 2.193x104, 9.213x104] whose graphical representation is depicted in Fig. (9). However, the approximate failure assessment value is calculated as 0.2063.
Example 3: Consider a beam of length L = 1300mm, height h = 8mm and the force density f = 78.5x10-5kN/mm3 with uncertain load w = Cauchy(400,1.5)kN bending moment is represented by the normal probability distributionand Mo = normal(2.05x105, 2.05x103)kN-mm breadth of the beam b = Gauss(40,15)mm.
Suppose the reference function (equation 13) is:
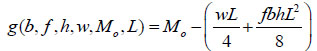 |
(13) |
Here also, it is needed to gauge the structural failure of the beam or credibility of failure.
In this problem, the representations of uncertain variables are both possibilistic and probabilistic. In such circumstances, FVs are converted into CDs and for the probability distribution, considers its cumulative distribution function form. Then, as usual, there is also a need to generate three random numbers (uniform) from [0, 1], say r1, s1 and t1. Using credibility sampling for credibility distributions Φw, ΦMo and Monte-Carlo sampling for probability distribution (CDF) Fb; three values Φ-1w(r1), Φ-1Mo(s1) and Φ-1b(s1) respectively can be obtained. Then, find:
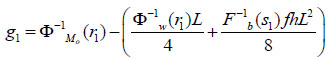 |
Here, if g1 > 0 then credibility value (Cr1) = 0 and if g1 < 0 then credibility value (Cr1) = 1 Proceeding in this way for N times for different random numbers, the failure assessment can be evaluated as 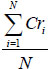 that are presented in Table 3 and the corresponding CD is depicted in Fig. (10).
that are presented in Table 3 and the corresponding CD is depicted in Fig. (10).
In this situation, the approach [23] is unable to calculate failure reliability.
Example 4: Consider a slab with a thickness (L) 10mm is insulted on one side at x = 0 are cooled by a fluid with bulk temperature 100oC. The produced heat (Q = 0) is 8x10-1w/m3.
The reference function (equation 14) is:
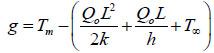 |
(14) |
The representation of the three uncertain variables heat transfer coefficient (h), thermal conductivity (k), and melting temperature (Tm) are fuzzy variables such as k = [5,20,40], h = [1500,4000,7500] and Tm = [500,800,1200]. It is needed to gauge failure assessment for this problem too.
Here also, the three uncertain variables k, h, Tm are converted into CDs and accordingly require to produce three uniform random numbers from [0,1] to get the value of the uncertain variables using credibility sampling. Finally, failure assessment is calculated and presented in Table 4, and the corresponding credibility distribution is depicted in Fig. (11).
| Sl.No | Failure Assessment | Simulation Number(N) |
|---|---|---|
| 1 | 0.2680 | 1000 |
| 2 | 0.2642 | 5000 |
| 3 | 0.2603 | 10000 |
| 4 | 0.2601 | 100000 |
| 5 | 0.2597 | 1000000 |
| Sl.No | Failure Assessment | simulation Number(N) |
|---|---|---|
| 1 | 0.6810 | 1000 |
| 2 | 0.6724 | 5000 |
| 3 | 0.6711 | 10000 |
| 4 | 0.6677 | 100000 |
| 5 | 0.6667 | 1000000 |
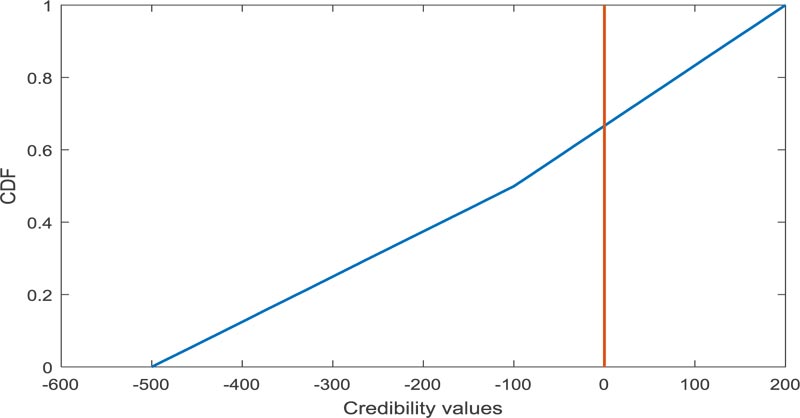
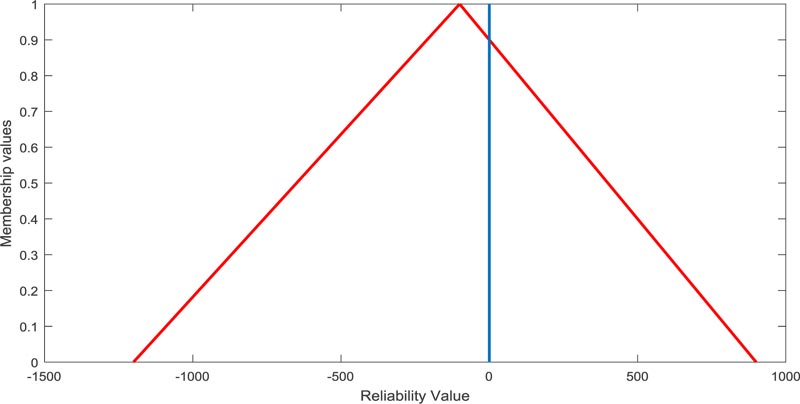
Failure of reliability via approach [23] in this case, is found to be [-1200, 100, 900], which is presented in Fig. (12) and its failure reliability value is found to be 0.5714.
5. RESULTS AND DISCUSSIONS
In the four structural reliability assessment problems, reliability assessment (or failure assessment) of a bar and heat transfer problem concerning the credibility of the melting of the slab are calculated using the proposed approach. In each problem 1000, 5000, 10000, 100000, and 1000000 simulations are considered to perform failure assessment. In the first problem, the representation of the parameters R and load S are FVs, and thus, they were transformed into CDs and failure assessments were evaluated. The calculated failure values are obtained as 0.2520, 0.2512, 0.2500, 0.2499, and 0.2498 for 1000, 5000, 10000, 100000, and 1000000 simulations, respectively. in the same way, in the second problem, the representation of the imprecise parameters w, b and Mo are FVs and similarly transformed into CDs. The estimated failure assessment values are 0.2530, 0.2442, 0.2422, 0.2417, and 0.2411 for the five sorts of simulations, respectively. The third problem is analogous to the second problem, but nature is simply like hybridization. Here, the depiction of Mo is that the probability distribution of normal type with mean and variance 40 and 15, respectively, while w and b are remain the same. By the assistance of Monte Carlo simulation and credibility simulation, structural failure values are evaluated using the proposed approach and which are 0.2680, 0.2642, 0.2603, 0.2601, and 0.2597, respectively. On the other hand, in the fourth problem of heat transfer problems, the credibility of the melting of the slab are evaluated where all the input uncertain variables are fuzzy variables. The estimated failure assessment values are 0.6810, 0.6724, 0.6711, 0.6677, and 0.6667, respectively, for the five categories of simulations.
The approach [21] also attempted to perform structural failure assessment where α values are precisely/directly taken from [0,1], which is more restrictive, but taking α values randomly is more permissive and realistic as well. Although the prevailing area-based approach can evaluate failure reliability, the technique presented in a previous study [23] is suitable just for linear input fuzzy variables and faces difficulties when input fuzzy variables are of various non-linear types and shapes. Furthermore, the approach fails when the system could be a more complex and hybrid type.
CONCLUSION
Owing to the presence of vagueness/imprecision within the parameters of structural reliability analysis, the available solution methods produce the matter of massive computationally difficult and inadequate precision. Therefore, to obviate this problem, an algorithm has been devised using credibility sampling. Four structural reliability analysis problems are solved. Comparative analysis was also administered and it was observed that despite having advantages of the prevailing approach, it has some limitations like the approach fails when the system may be a more complex and hybrid type. It was found that the proposed approach is efficient, simple, logical, technically sound, and general enough for implementation.
After evaluation of failure assessment, it was experienced that the rise within the number of simulations results in better precision. Furthermore, it was also encountered that when hybridization problems, i.e., representation of imprecise components within the problem of structural failure are both fuzzy and probabilistic nature, and then the failure assessment is attained to be maximum. As an extension of this work, intuitionistic fuzzy numbers and type-2 fuzzy numbers are going to be taken into consideration to represent uncertainty, and accordingly, similar sorts of study are going to be performed.
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
The authors confirm that the data supporting the findings of this study are available within the article.
FUNDING
None.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.


