RESEARCH ARTICLE
Minimum Depth-Span Ratio of Beams in order to Control Maximum Permissible Deflection
Mereen H. Fahmi Rasheed1, Ayad Zeki Saber Agha1, *
Article Information
Identifiers and Pagination:
Year: 2020Volume: 14
First Page: 402
Last Page: 414
Publisher ID: TOCIEJ-14-402
DOI: 10.2174/1874149502014010402
Article History:
Received Date: 07/08/2020Revision Received Date: 02/11/2020
Acceptance Date: 21/11/2020
Electronic publication date: 31/12/2020
Collection year: 2020

open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: https://creativecommons.org/licenses/by/4.0/legalcode. This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Background:
ACI code and other building codes and standards include the provisions for deflection control and depth-span limitations, also including the maximum permissible deflection for specified concrete and steel reinforcement strength. In this study, the effects of applied load intensity, steel reinforcement index amount as a ratio to the balancing reinforcement index (ρ/ρb), concrete strength (fc' ) and beam width on the depth-span ratio of the beam with different types (simply supported, fixed ended, propped and cantilever) were investigated.
Objective:
This study aimed to study the effect of applied load intensity, steel reinforcement index amount as a ratio to the balancing reinforcement index (ρ/ρb), concrete strength (fc' ) and beam width on the depth-span ratio of the beam of different types (simply supported, fixed ended, propped and cantilever).
Methods:
This study theoretically investigates the effect of applied load intensity, steel reinforcement index amount as a ratio to the balancing reinforcement index (ρ/ρb), concrete strength (fc' ) and beam width on the depth-span ratio of the beam of different types (simply supported, fixed ended, propped and cantilever).
Results:
The results show that the effect of the ratio (ρ/ρb) is small on the depth-span ratio, and the required depth of the beam increased with increasing the applied distributed load value and decreased with increasing the concrete strength for all beam types.
Discussion:
Deflection of slabs and beams can be controlled by the addition of steel reinforcement bars or using pre-stressing concrete, loading type and value, material properties (E), section properties (I), and the type of the member. The results showed that the effect of the ratio (ρ/ρb) was small on the depth-span ratio, and the required depth of the beam increased with increasing the applied distributed load value and decreased with increasing the concrete strength for all beam types.
Conclusion:
- A modification of ACI Code span-depth ratio is suggested to include the effect of tension reinforcement area which is represented by the reinforcement indices ratio (ρ/ρb), applied distributed load (w), concrete compressive strength (fc' ) and cross section width (b) in order to control the maximum deflection of the beam within the ACI limit of the maximum permitted deflection.
- The value of span-depth ratio (N = L / h) is determined for four types of beam (simply supported, fixed ended, propped and cantilever) for concrete strengths (fc' = 21, 28, 35, 42, 63 & 84 MPa), applied distributed load (w = 14.6, 29.2, 43.8 & 58.4 kN/m), cross width (b = 150, 200, 250 & 300 mm) and (ρ/ρb = 0, 0.5 & 1) in addition to (ρt /ρb & ρmax /ρb).
- The effect of the reinforced indicia ratio (ρ/ρb) is small on the span-depth ratio (N = L / h) for all values of applied load and concrete compressive strength.
- The span-depth ratio (N = L / h) decreased with increasing the applied load, or in other words, the required depth increased with increasing the applied load for all values of concrete strength and beam width.
- The span-depth ratio (N = L / h) increased with increasing the concrete strength (fc' ), i.e. the required depth decreased with increasing concrete strength for all values of applied loads and beam width.
- The same behavior and conclusions are obtained for all beam types (simply supported, fixed ended, propped and cantilever).
1. INTRODUCTION
Deflection of slabs and beams can be controlled by the addition of steel reinforcement bars in tension and compression zones or using pre-stressing concrete. In addition to that, deflection is influenced by different factors such as loading type and value, material properties (E), section properties (I), type of the member i.e. type of the boundary condition (simply supported, fixed or free), and time dependent or long term deflection due to creep and shrinkage of concrete during the life of the structure.
Deflection control in different building codes and standards is determined by two approaches,
- Indirect method, by assuming suitable upper limits on the depth-span ratio which is satisfactory for many cases of spans, load distribution, member size and properties.
- Direct method by calculating the deflection for the actual case and comparing the results with the specific limitations of the codes and standards.
Generally, the deflection is determined when the member is loaded by the normal full-service load to ensure that stresses in the stream fiber in both steel and concrete remain in elastic range, i.e. the un-cracked section properties are used to calculate the immediate deflection [1-7].
Lee et al. [8], compared provisions of different codes and standards about minimum thickness. They concluded that the CSA and ACI provisions have limited application and the proposed equation is recommended for calculation of the minimum thickness. Beal and Thomasen [9], presented an approximated depth-span ratio for the preliminary design specification in terms of (M/bd2) rather than (As/bd) to include the effect of steel design stress. Shehata et al. [10], presented a theoretical study for the minimum steel ratio required for bending, shear and torsion for beams with different concrete strengths.
Orvin and Anik [11], determined the minimum thickness of reinforced concrete slabs to resist undesirable vibrations and compared the results with other studies. They conclude that the American Concrete Institute (ACI) minimum thickness limit is not satisfactory for vibration. Three-dimensional finite element modelling was carried out to study the natural floor vibration, and the results were verified by the ANSYS model and Etabs modelling. Several parameters such as slab thickness, span length and floor panel aspect ratio were taken into consideration
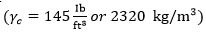 .
.
ACI code [1] provides the minimum depth for one-way slabs and beams shown in Table 1, for non-prestressed members, normal concrete weight (γc = 145 lb/ft3 or 2320 kg/m3) and steel yielding strength (= 60,000 psi or 414 MPa). Correction factors are used for lightweight concrete with density in the range 90-115 lb/ft3 or 1440-1840 kg/m3 and yielding strength other than (60000 psi) as shown below:
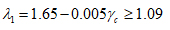 |
(1) |
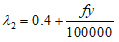 |
(2) |
Generally, the deflection is a function of the load value and type applied on the member, span length, and beam cross-section, which is represented by the moment of inertia (I), material properties which are represented by the modulus of elasticity (E) and support condition of both ends, that is the member type (simply supported, fixed ended, propped and cantilever).
Islam Khan et al. [12], investigated the reinforced concrete building by using three-dimensional finite element modeling to determine the minimum slab thickness to prevent undesirable vibration. The developed finite element model was applied in previous experiments which validated the applicability of the model for further parametric study. Different slab thickness, span length and floor aspect ratio were studied. An empirical equation is given which provides minimum slab thickness of a short span reinforced concrete building.
Ho et al. [13], developed a simplified method for providing minimum flexural ductility and evaluation of maximum values of tension steel ratio and neutral axis depth corresponding to the proposed minimum curvature ductility factor for various concrete grades and steel yielding strengths. Akmaluddin [14], presented an improved model of the effective moment of inertia to predict the short-term deflection of reinforced lightweight concrete beam. The proposed model is verified and compared with experimental results of nine beams; good agreement is obtained with the experimental results and in some cases, a similar trend was observed for the ACI and SNI provisions.
The elastic deflection can be expressed in the following form [2-7]:
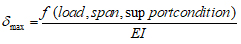 |
(3) |
| Support type | One way slab | Beam |
|---|---|---|
| Simply supported | L/20 | L/16 |
| One end continuous (propped) | L/24 | L/18.5 |
| Two end continuous (fixed ended) | L/28 | L/21 |
| Cantilever | L/10 | L/8 |
Where f is a function of the load type and value (distributed load or concentrated load), span length and support conditions, Table 2 shows the maximum deflection of different type beams and loadings [15-17].
Where:
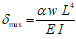 For distributed load.
For distributed load.
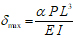 For concentrated load.
For concentrated load.
| Support type | Loading type | α |
|---|---|---|
| Simply supported | Uniform distributed load | 5/384 |
| One end continuous (propped) | Uniform distributed load | 1/185 |
| Two ends continuous (fixed ended) | Uniform distributed load | 1/384 |
| Cantilever | Uniform distributed load | 1/8 |
| Simply supported | Concentrated load at midspan | 1/48 |
| One end continuous (propped) | Concentrated load at midspan | 1/(48√5) |
| Two ends continuous (fixed ended) | Concentrated load at midspan | 1/192 |
| Cantilever | Concentrated load at free end | 1/3 |
2. MATERIALS AND METHODS
The effective moment of inertia (Ie) is used, which lies between cracking and uncracked section; the moment of inertia can be determined from the following equation [1-6]:
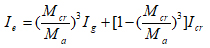 |
(4) |
where:
Ie = Effective moment of inertia (mm4).
Icr = Moment of inertia of cracked transformed section (mm4).
Ig = Moment of inertia of un-cracked transformed section (mm4).
Ma = Maximum bending moment due to the service load (kN.mm).
Mcr = Cracking bending moment due to service load and equal to
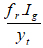
fr = Modulus of rupture of the concrete (MPa).
yt = Distance from the neutral axis of the section to the extreme fiber at the
tension face (mm) and calculated from the following equation:
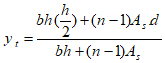 |
(5) |
Where:
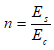
Es = Modulus of elasticity of steel reinforcement (MPa) = 200,000 MPa
Ec = Modulus of elasticity of the concrete (MPa) =
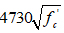
d = Effective depth of the cross-section which is assumed to be equal to (0.85h), (mm)
As = Area of tensile steel reinforcement in the section (mm2)
b = Width of the section (mm)
h = Total depth of the section (mm)
Taking As = pbd and d = 0.85h, equation (5) can be simplified to:
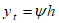 |
(6) |
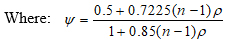 |
(7) |
The total moment of inertia of the transformed un-cracked section is equal to:
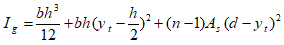 |
(8) |
This equation simplified to the following form:
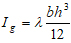 |
(9) |
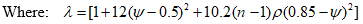 |
(10) |
The cracking moment of inertia (Icr) is determined for the cracked transformed section:
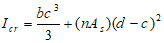 |
(11) |
Where (c) is the depth of the compressive zone at the cracked condition, and determined as follows:
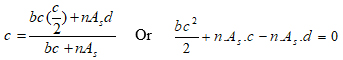 |
(12) |
This equation is solved by the quadratic equation method to find the value of (c).
The effect of the reinforcement and concrete compressive strength (fc' ) are included to find the modified correction factor based on the results of ACI-Code minimum thickness shown in Table 1, and based on the maximum allowable deflection permitted by ACI-Code shown in Table 3.
In this study, the allowable maximum deflection ratio (δmax/L) is taken to be not greater than the ACI-limit (1/360), that is:
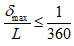 |
(13) |
According to eq. (3) and results of Table 2, the maximum deflection for beams or one way slabs subjected to uniform distributed load can be determined as:
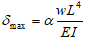 |
(14) |
Where α is constant, depending on the type of supports, as shown in Table 2.
Substituting (δmax) from eq. (14) into eq. (13), the required moment of inertia (Ireq) is determined as:
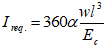 |
(15) |
Taking
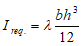
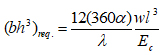 |
(16) |
The depth-span (h/L) ratio can be determined from the next equation:
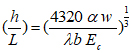 |
(17) |
The depth-span ratio calculated from eq. (17) is the minimum ratio in order to control the limit of maximum deflection within the ACI-maximum deflection limit.
Taking and from eq. (17), the value of (N) is determined for different values of applied load (w), concrete compressive strength (fc' ) that is used to find (Ec) and cross section width (b) for simply supported, fixed ended, propped and cantilever beams.
Table 4, show the results of span-depth ratio (N = L / h) for simply supported beam for concrete compressive strength (fc' = 21, 28, 35, 42, 63 and 84 MPa), applied distributed load (w= 14.6, 29.2, 43.8, and 58.4 KN/m) and cross section width (b= 150, 200, 250 and 300 mm).
Table 5, shows the results of (L/h) for fixed ended beam. Table 6 shows the results of propped beam and Table 7 shows cantilever beam for different values of the variables (, w and b).
Value of (λ) is determined from eq. (10), for different values of reinforcement index (ρ) taking (ρ/ρb) varying from 0for section without reinforcement to (1), in addition to ρt and ρmax.
Where
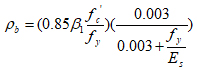 |
(18) |
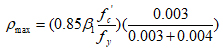 |
(19) |
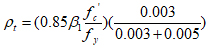 |
(20) |
The effects of the reinforcement indices ratio (ρ/ρb), concrete compressive ratio (fc' ) and the applied load (w) on the span-depth ratio (N = L / h) for simply supported, fixed ended, propped and cantilever beams are shown in the following figures.
| Type of Member | Deflection to be considered | Deflection Limitation |
|---|---|---|
| Flat roofs not supporting or attached to nonstructural elements likely to be damaged by large deflection | Immediate deflection due to the live load L | 1/180 |
| Floors not supporting or attached to nonstructural elements likely to be damaged by large deflection | Immediate deflection due to the live load L | 1/360 |
| Roof or floor construction supporting or attached to nonstructural elements likely to be damaged by large deflection | The part of the total deflection occurring after attachment of the nonstructural element (sum of the long-time deflection due to all sustained loads and the immediate deflection due to any additional live load) | 1/480 |
| Roof or floor construction supporting or attached to nonstructural elements not likely to be damaged by large deflection | 1/240 |
| α = 0.0130" | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| - | fc' = 3000 (psi) = 21 (MPa) | fc' = 4000 (psi) = 28 (MPa) | fc' = 5000 (psi) = 35 (MPa) | fc' = 6000 (psi) = 42 (MPa) | fc' = 9000 (psi) = 63 (MPa) | fc' = 12000 (psi) = 84 (MPa) | ||||||||||||||||||
| b (in) | 6 | 8 | 10 | 12 | 6 | 8 | 10 | 12 | 6 | 8 | 10 | 12 | 6 | 8 | 10 | 12 | 6 | 8 | 10 | 12 | 6 | 8 | 10 | 12 |
| b (mm) | 150 | 200 | 250 | 300 | 150 | 200 | 250 | 300 | 150 | 200 | 250 | 300 | 150 | 200 | 250 | 300 | 150 | 200 | 250 | 300 | 150 | 200 | 250 | 300 |
| - | w = "1 kips/ft = 14.6 kN/m" | |||||||||||||||||||||||
| ρ = 0 | 15.9 | 17.5 | 18.8 | 20.0 | 16.6 | 18.3 | 19.7 | 21.0 | 17.3 | 19.0 | 20.5 | 21.8 | 17.8 | 19.6 | 21.1 | 22.4 | 19.1 | 21.0 | 22.6 | 24.0 | 20.0 | 22.0 | 23.7 | 25.2 |
| ρ = 0.5 ρb | 16.4 | 18.0 | 19.4 | 20.7 | 17.3 | 19.0 | 20.5 | 21.8 | 17.9 | 19.7 | 21.3 | 22.6 | 18.5 | 20.4 | 21.9 | 23.3 | 19.6 | 21.6 | 23.3 | 24.7 | 20.6 | 22.7 | 24.5 | 26.0 |
| ρ = ρmax = 0.634ρb | 16.5 | 18.2 | 19.6 | 20.8 | 17.4 | 19.2 | 20.6 | 21.9 | 18.1 | 19.9 | 21.4 | 22.8 | 18.6 | 20.4 | 22.0 | 23.4 | 19.8 | 21.8 | 23.5 | 24.9 | 20.9 | 23.0 | 24.7 | 26.3 |
| ρ = ρt = 0.724ρb | 16.6 | 18.3 | 19.7 | 20.9 | 17.5 | 19.3 | 20.8 | 22.1 | 18.2 | 20.0 | 21.5 | 22.9 | 18.7 | 20.5 | 22.1 | 23.5 | 19.9 | 21.9 | 23.6 | 25.1 | 21.0 | 23.1 | 24.9 | 26.4 |
| ρ = ρb | 16.8 | 18.5 | 19.9 | 21.2 | 17.8 | 19.5 | 21.1 | 22.4 | 18.4 | 20.3 | 21.9 | 23.2 | 19.0 | 21.0 | 22.6 | 24.0 | 20.1 | 22.1 | 23.8 | 25.3 | 21.2 | 23.3 | 25.1 | 26.7 |
| Avg. = | 16.4 | 18.1 | 19.5 | 20.7 | 17.3 | 19.1 | 20.5 | 21.8 | 18.0 | 19.8 | 21.3 | 22.7 | 18.5 | 20.4 | 21.9 | 23.3 | 19.7 | 21.7 | 23.3 | 24.8 | 20.7 | 22.8 | 24.6 | 26.1 |
| - | w = "2 kips/ft = 29.2 kN/m" | |||||||||||||||||||||||
| ρ = 0 | 12.6 | 13.9 | 14.9 | 15.9 | 13.2 | 14.5 | 15.7 | 16.6 | 13.7 | 15.1 | 16.3 | 17.3 | 14.1 | 15.6 | 16.8 | 17.8 | 15.1 | 16.6 | 17.9 | 19.1 | 15.9 | 17.5 | 18.8 | 20.0 |
| ρ = 0.5 ρb | 13.0 | 14.3 | 15.4 | 16.4 | 13.7 | 15.1 | 16.2 | 17.3 | 14.2 | 15.7 | 16.9 | 17.9 | 14.7 | 16.2 | 17.4 | 18.5 | 15.6 | 17.1 | 18.5 | 19.6 | 16.4 | 18.0 | 19.4 | 20.6 |
| ρ = ρmax = 0.634ρb | 13.1 | 14.4 | 15.5 | 16.5 | 13.8 | 15.2 | 16.4 | 17.4 | 14.4 | 15.8 | 17.0 | 18.1 | 14.7 | 16.2 | 17.5 | 18.6 | 15.7 | 17.3 | 18.6 | 19.8 | 16.6 | 18.2 | 19.6 | 20.9 |
| ρ = ρt = 0.724ρb | 13.2 | 14.5 | 15.6 | 16.6 | 13.9 | 15.3 | 16.5 | 17.5 | 14.4 | 15.9 | 17.1 | 18.2 | 14.8 | 16.3 | 17.6 | 18.7 | 15.8 | 17.4 | 18.7 | 19.9 | 16.6 | 18.3 | 19.7 | 21.0 |
| ρ = ρb | 13.4 | 14.7 | 15.8 | 16.8 | 14.1 | 15.5 | 16.7 | 17.8 | 14.6 | 16.1 | 17.4 | 18.4 | 15.1 | 16.6 | 17.9 | 19.0 | 15.9 | 17.5 | 18.9 | 20.1 | 16.8 | 18.5 | 19.9 | 21.2 |
| Avg. = | 13.0 | 14.4 | 15.5 | 16.4 | 13.7 | 15.1 | 16.3 | 17.3 | 14.3 | 15.7 | 16.9 | 18.0 | 14.7 | 16.2 | 17.4 | 18.5 | 15.6 | 17.2 | 18.5 | 19.7 | 16.5 | 18.1 | 19.5 | 20.7 |
| - | w = "3 kips/ft = 4.08 kN/m" | |||||||||||||||||||||||
| ρ = 0 | 11.0 | 12.1 | 13.0 | 13.9 | 11.5 | 12.7 | 13.7 | 14.5 | 12.0 | 13.2 | 14.2 | 15.1 | 12.4 | 13.6 | 14.6 | 15.6 | 13.2 | 14.5 | 15.7 | 16.6 | 13.9 | 15.3 | 16.4 | 17.5 |
| ρ = 0.5 ρb | 11.4 | 12.5 | 13.5 | 14.3 | 12.0 | 13.2 | 14.2 | 15.1 | 12.4 | 13.7 | 14.7 | 15.7 | 12.8 | 14.1 | 15.2 | 16.2 | 13.6 | 15.0 | 16.1 | 17.1 | 14.3 | 15.8 | 17.0 | 18.0 |
| ρ = ρmax = 0.634ρb | 11.5 | 12.6 | 13.6 | 14.4 | 12.1 | 13.3 | 14.3 | 15.2 | 12.5 | 13.8 | 14.9 | 15.8 | 12.9 | 14.2 | 15.3 | 16.2 | 13.7 | 15.1 | 16.3 | 17.3 | 14.5 | 15.9 | 17.1 | 18.2 |
| ρ = ρt = 0.724ρb | 11.5 | 12.7 | 13.6 | 14.5 | 12.1 | 13.4 | 14.4 | 15.3 | 12.6 | 13.9 | 14.9 | 15.9 | 12.9 | 14.2 | 15.3 | 16.3 | 13.8 | 15.2 | 16.4 | 17.4 | 14.5 | 16.0 | 17.2 | 18.3 |
| ρ = ρb | 11.7 | 12.8 | 13.8 | 14.7 | 12.3 | 13.6 | 14.6 | 15.5 | 12.8 | 14.1 | 15.2 | 16.1 | 13.2 | 14.5 | 15.7 | 16.6 | 13.9 | 15.3 | 16.5 | 17.5 | 14.7 | 16.2 | 17.4 | 18.5 |
| Avg. = | 11.4 | 12.5 | 13.5 | 14.4 | 12.0 | 13.2 | 14.2 | 15.1 | 12.5 | 13.7 | 14.8 | 15.7 | 12.8 | 14.1 | 15.2 | 16.2 | 13.7 | 15.0 | 16.2 | 17.2 | 14.4 | 15.8 | 17.0 | 18.1 |
| - | w = "4 kips/ft = 58.4 kN/m" | |||||||||||||||||||||||
| ρ = 0 | 10.0 | 11.0 | 11.9 | 12.6 | 10.5 | 11.5 | 12.4 | 13.2 | 10.9 | 12.0 | 12.9 | 13.7 | 11.2 | 12.4 | 13.3 | 14.1 | 12.0 | 13.2 | 14.2 | 15.1 | 12.6 | 13.9 | 14.9 | 15.9 |
| ρ = 0.5 ρb | 10.3 | 11.4 | 12.2 | 13.0 | 10.9 | 12.0 | 12.9 | 13.7 | 11.3 | 12.4 | 13.4 | 14.2 | 11.7 | 12.8 | 13.8 | 14.7 | 12.4 | 13.6 | 14.7 | 15.6 | 13.0 | 14.3 | 15.4 | 16.4 |
| ρ = ρmax = 0.634ρb | 10.4 | 11.5 | 12.3 | 13.1 | 11.0 | 12.1 | 13.0 | 13.8 | 11.4 | 12.5 | 13.5 | 14.4 | 11.7 | 12.9 | 13.9 | 14.7 | 12.5 | 13.7 | 14.8 | 15.7 | 13.1 | 14.5 | 15.6 | 16.6 |
| ρ = ρt = 0.724ρb | 10.5 | 11.5 | 12.4 | 13.2 | 11.0 | 12.1 | 13.1 | 13.9 | 11.4 | 12.6 | 13.6 | 14.4 | 11.8 | 12.9 | 13.9 | 14.8 | 12.5 | 13.8 | 14.9 | 15.8 | 13.2 | 14.5 | 15.7 | 16.6 |
| ρ = ρb | 10.6 | 11.7 | 12.6 | 13.4 | 11.2 | 12.3 | 13.3 | 14.1 | 11.6 | 12.8 | 13.8 | 14.6 | 12.0 | 13.2 | 14.2 | 15.1 | 12.7 | 13.9 | 15.0 | 15.9 | 13.3 | 14.7 | 15.8 | 16.8 |
| Avg. = | 10.4 | 11.4 | 12.3 | 13.0 | 10.9 | 12.0 | 12.9 | 13.7 | 11.3 | 12.5 | 13.4 | 14.3 | 11.7 | 12.8 | 13.8 | 14.7 | 12.4 | 13.7 | 14.7 | 15.6 | 13.1 | 14.4 | 15.5 | 16.5 |
| α = 0.0026 | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| - | fc' = 3000 (psi) = 21 (MPa) | fc' = 4000 (psi) = 28 (MPa) | fc' = 5000 (psi) = 35 (MPa) | fc' = 6000 (psi) = 42 (MPa) | fc' = 9000 (psi) = 63 (MPa) | fc' = 12000 (psi) = 84 (MPa) | ||||||||||||||||||
| b (in) | 6 | 8 | 10 | 12 | 6 | 8 | 10 | 12 | 6 | 8 | 10 | 12 | 6 | 8 | 10 | 12 | 6 | 8 | 10 | 12 | 6 | 8 | 10 | 12 |
| b (mm) | 150 | 200 | 250 | 300 | 150 | 200 | 250 | 300 | 150 | 200 | 250 | 300 | 150 | 200 | 250 | 300 | 150 | 200 | 250 | 300 | 150 | 200 | 250 | 300 |
| - | w = "1 kips/ft = 14.6 kN/m" | |||||||||||||||||||||||
| ρ = 0 | 27.1 | 29.9 | 32.2 | 34.2 | 28.5 | 31.3 | 33.8 | 35.9 | 29.5 | 32.5 | 35.0 | 37.2 | 30.5 | 33.5 | 36.1 | 38.4 | 32.6 | 35.9 | 38.6 | 41.1 | 34.2 | 37.6 | 40.5 | 43.1 |
| ρ = 0.5 ρb | 28.0 | 30.9 | 33.2 | 35.3 | 29.5 | 32.5 | 35.0 | 37.2 | 30.7 | 33.8 | 36.4 | 38.6 | 31.6 | 34.8 | 37.5 | 39.8 | 33.5 | 36.9 | 39.8 | 42.3 | 35.3 | 38.8 | 41.8 | 44.5 |
| ρ = ρmax = 0.634ρb | 28.2 | 31.1 | 33.5 | 35.6 | 29.8 | 32.8 | 35.3 | 37.5 | 30.9 | 34.0 | 36.7 | 39.0 | 31.7 | 34.9 | 37.6 | 40.0 | 33.9 | 37.3 | 40.1 | 42.7 | 35.7 | 39.3 | 42.3 | 44.9 |
| ρ = ρt = 0.724ρb | 28.4 | 31.2 | 33.6 | 35.8 | 29.9 | 32.9 | 35.5 | 37.7 | 31.1 | 34.2 | 36.8 | 39.1 | 31.9 | 35.1 | 37.8 | 40.2 | 34.0 | 37.5 | 40.4 | 42.9 | 35.9 | 39.5 | 42.5 | 45.2 |
| ρ = ρb | 28.8 | 31.7 | 34.1 | 36.2 | 30.4 | 33.4 | 36.0 | 38.3 | 31.5 | 34.7 | 37.4 | 39.7 | 32.6 | 35.8 | 38.6 | 41.0 | 34.3 | 37.8 | 40.7 | 43.3 | 36.2 | 39.8 | 42.9 | 45.6 |
| Avg. = | 28.1 | 30.9 | 33.3 | 35.4 | 29.6 | 32.6 | 35.1 | 37.3 | 30.7 | 33.8 | 36.5 | 38.7 | 31.7 | 34.8 | 37.5 | 39.9 | 33.7 | 37.1 | 39.9 | 42.4 | 35.4 | 39.0 | 42.0 | 44.7 |
| - | w = "2 kips/ft = 29.2 kN/m" | |||||||||||||||||||||||
| ρ = 0 | 21.5 | 23.7 | 25.5 | 27.1 | 22.6 | 24.9 | 26.8 | 28.5 | 23.5 | 25.8 | 27.8 | 29.5 | 24.2 | 26.6 | 28.7 | 30.5 | 25.9 | 28.5 | 30.7 | 32.6 | 27.1 | 29.9 | 32.2 | 34.2 |
| ρ = 0.5 ρb | 22.2 | 24.5 | 26.4 | 28.0 | 23.4 | 25.8 | 27.8 | 29.5 | 24.3 | 26.8 | 28.9 | 30.7 | 25.1 | 27.6 | 29.8 | 31.6 | 26.6 | 29.3 | 31.6 | 33.5 | 28.0 | 30.8 | 33.2 | 35.3 |
| ρ = ρmax = 0.634ρb | 22.4 | 24.7 | 26.6 | 28.2 | 23.6 | 26.0 | 28.0 | 29.8 | 24.5 | 27.0 | 29.1 | 30.9 | 25.2 | 27.7 | 29.9 | 31.7 | 26.9 | 29.6 | 31.9 | 33.9 | 28.3 | 31.2 | 33.6 | 35.7 |
| ρ = ρt = 0.724ρb | 22.5 | 24.8 | 26.7 | 28.4 | 23.8 | 26.1 | 28.2 | 29.9 | 24.7 | 27.1 | 29.2 | 31.1 | 25.3 | 27.9 | 30.0 | 31.9 | 27.0 | 29.7 | 32.0 | 34.0 | 28.5 | 31.3 | 33.7 | 35.9 |
| ρ = ρb | 22.8 | 25.1 | 27.1 | 28.8 | 24.1 | 26.5 | 28.6 | 30.4 | 25.0 | 27.5 | 29.7 | 31.5 | 25.8 | 28.4 | 30.6 | 32.6 | 27.3 | 30.0 | 32.3 | 34.3 | 28.7 | 31.6 | 34.1 | 36.2 |
| Avg. = | 22.3 | 24.6 | 26.5 | 28.1 | 23.5 | 25.9 | 27.9 | 29.6 | 24.4 | 26.9 | 28.9 | 30.7 | 25.1 | 27.7 | 29.8 | 31.7 | 26.7 | 29.4 | 31.7 | 33.7 | 28.1 | 31.0 | 33.4 | 35.4 |
| - | w = "3 kips/ft = 4.08 kN/m" | |||||||||||||||||||||||
| ρ = 0 | 18.8 | 20.7 | 22.3 | 23.7 | 19.7 | 21.7 | 23.4 | 24.9 | 20.5 | 22.5 | 24.3 | 25.8 | 21.1 | 23.2 | 25.0 | 26.6 | 22.6 | 24.9 | 26.8 | 28.5 | 23.7 | 26.1 | 28.1 | 29.9 |
| ρ = 0.5 ρb | 19.4 | 21.4 | 23.0 | 24.5 | 20.5 | 22.5 | 24.3 | 25.8 | 21.3 | 23.4 | 25.2 | 26.8 | 21.9 | 24.1 | 26.0 | 27.6 | 23.3 | 25.6 | 27.6 | 29.3 | 24.5 | 26.9 | 29.0 | 30.8 |
| ρ = ρmax = 0.634ρb | 19.6 | 21.6 | 23.2 | 24.7 | 20.6 | 22.7 | 24.5 | 26.0 | 21.4 | 23.6 | 25.4 | 27.0 | 22.0 | 24.2 | 26.1 | 27.7 | 23.5 | 25.8 | 27.8 | 29.6 | 24.7 | 27.2 | 29.3 | 31.2 |
| ρ = ρt = 0.724ρb | 19.7 | 21.7 | 23.3 | 24.8 | 20.8 | 22.8 | 24.6 | 26.1 | 21.5 | 23.7 | 25.5 | 27.1 | 22.1 | 24.3 | 26.2 | 27.9 | 23.6 | 26.0 | 28.0 | 29.7 | 24.9 | 27.4 | 29.5 | 31.3 |
| ρ = ρb | 19.9 | 22.0 | 23.6 | 25.1 | 21.1 | 23.2 | 25.0 | 26.5 | 21.9 | 24.1 | 25.9 | 27.5 | 22.6 | 24.8 | 26.8 | 28.4 | 23.8 | 26.2 | 28.2 | 30.0 | 25.1 | 27.6 | 29.8 | 31.6 |
| Avg. = | 19.5 | 21.5 | 23.1 | 24.6 | 20.5 | 22.6 | 24.3 | 25.9 | 21.3 | 23.5 | 25.3 | 26.9 | 21.9 | 24.2 | 26.0 | 27.7 | 23.3 | 25.7 | 27.7 | 29.4 | 24.6 | 27.0 | 29.1 | 31.0 |
| - | w = "4 kips/ft = 58.4 kN/m" | |||||||||||||||||||||||
| ρ = 0 | 17.1 | 18.8 | 20.3 | 21.5 | 17.9 | 19.7 | 21.3 | 22.6 | 18.6 | 20.5 | 22.1 | 23.5 | 19.2 | 21.1 | 22.7 | 24.2 | 20.5 | 22.6 | 24.3 | 25.9 | 21.5 | 23.7 | 25.5 | 27.1 |
| ρ = 0.5 ρb | 17.7 | 19.4 | 20.9 | 22.2 | 18.6 | 20.5 | 22.1 | 23.4 | 19.3 | 21.3 | 22.9 | 24.3 | 19.9 | 21.9 | 23.6 | 25.1 | 21.1 | 23.3 | 25.1 | 26.6 | 22.2 | 24.5 | 26.4 | 28.0 |
| ρ = ρmax = 0.634ρb | 17.8 | 19.6 | 21.1 | 22.4 | 18.8 | 20.6 | 22.2 | 23.6 | 19.5 | 21.4 | 23.1 | 24.5 | 20.0 | 22.0 | 23.7 | 25.2 | 21.3 | 23.5 | 25.3 | 26.9 | 22.5 | 24.7 | 26.6 | 28.3 |
| ρ = ρt = 0.724ρb | 17.9 | 19.7 | 21.2 | 22.5 | 18.9 | 20.8 | 22.4 | 23.8 | 19.6 | 21.5 | 23.2 | 24.7 | 20.1 | 22.1 | 23.8 | 25.3 | 21.4 | 23.6 | 25.4 | 27.0 | 22.6 | 24.9 | 26.8 | 28.5 |
| ρ = ρb | 18.1 | 19.9 | 21.5 | 22.8 | 19.1 | 21.1 | 22.7 | 24.1 | 19.9 | 21.9 | 23.6 | 25.0 | 20.5 | 22.6 | 24.3 | 25.8 | 21.6 | 23.8 | 25.6 | 27.3 | 22.8 | 25.1 | 27.0 | 28.7 |
| Avg. = | 17.7 | 19.5 | 21.0 | 22.3 | 18.7 | 20.5 | 22.1 | 23.5 | 19.4 | 21.3 | 23.0 | 24.4 | 19.9 | 21.9 | 23.6 | 25.1 | 21.2 | 23.3 | 25.1 | 26.7 | 22.3 | 24.6 | 26.5 | 28.1 |
| α = 0.0054 | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| - | fc' = 3000 (psi) = 21 (MPa) | fc' = 4000 (psi) = 28 (MPa) | fc' = 5000 (psi) = 35 (MPa) | fc' = 6000 (psi) = 42 (MPa) | fc' = 9000 (psi) = 63 (MPa) | fc' = 12000 (psi) = 84 (MPa) | ||||||||||||||||||
| b (in) | 6 | 8 | 10 | 12 | 6 | 8 | 10 | 12 | 6 | 8 | 10 | 12 | 6 | 8 | 10 | 12 | 6 | 8 | 10 | 12 | 6 | 8 | 10 | 12 |
| b (mm) | 150 | 200 | 250 | 300 | 150 | 200 | 250 | 300 | 150 | 200 | 250 | 300 | 150 | 200 | 250 | 300 | 150 | 200 | 250 | 300 | 150 | 200 | 250 | 300 |
| - | w = "1 kips/ft = 14.6 kN/m" | |||||||||||||||||||||||
| ρ = 0 | 21.3 | 23.4 | 25.2 | 26.8 | 22.3 | 24.6 | 26.5 | 28.1 | 23.2 | 25.5 | 27.5 | 29.2 | 23.9 | 26.3 | 28.3 | 30.1 | 25.5 | 28.1 | 30.3 | 32.2 | 26.8 | 29.5 | 31.8 | 33.8 |
| ρ = 0.5 ρb | 22.0 | 24.2 | 26.1 | 27.7 | 23.1 | 25.5 | 27.4 | 29.2 | 24.0 | 26.5 | 28.5 | 30.3 | 24.8 | 27.3 | 29.4 | 31.2 | 26.3 | 28.9 | 31.2 | 33.1 | 27.7 | 30.5 | 32.8 | 34.9 |
| ρ = ρmax = 0.634ρb | 22.1 | 24.4 | 26.2 | 27.9 | 23.3 | 25.7 | 27.7 | 29.4 | 24.2 | 26.7 | 28.7 | 30.5 | 24.9 | 27.4 | 29.5 | 31.3 | 26.5 | 29.2 | 31.5 | 33.4 | 28.0 | 30.8 | 33.2 | 35.2 |
| ρ = ρt = 0.724ρb | 22.2 | 24.5 | 26.4 | 28.0 | 23.5 | 25.8 | 27.8 | 29.6 | 24.4 | 26.8 | 28.9 | 30.7 | 25.0 | 27.5 | 29.6 | 31.5 | 26.7 | 29.4 | 31.6 | 33.6 | 28.1 | 30.9 | 33.3 | 35.4 |
| ρ = ρb | 22.5 | 24.8 | 26.7 | 28.4 | 23.8 | 26.2 | 28.2 | 30.0 | 24.7 | 27.2 | 29.3 | 31.1 | 25.5 | 28.1 | 30.3 | 32.2 | 26.9 | 29.6 | 31.9 | 33.9 | 28.4 | 31.2 | 33.6 | 35.8 |
| Avg. = | 22.0 | 24.3 | 26.1 | 27.8 | 23.2 | 25.6 | 27.5 | 29.2 | 24.1 | 26.5 | 28.6 | 30.4 | 24.8 | 27.3 | 29.4 | 31.3 | 26.4 | 29.1 | 31.3 | 33.3 | 27.8 | 30.6 | 32.9 | 35.0 |
| - | w = "2 kips/ft = 29.2 kN/m" | |||||||||||||||||||||||
| ρ = 0 | 16.9 | 18.6 | 20.0 | 21.3 | 17.7 | 19.5 | 21.0 | 22.3 | 18.4 | 20.2 | 21.8 | 23.2 | 19.0 | 20.9 | 22.5 | 23.9 | 20.3 | 22.3 | 24.0 | 25.5 | 21.3 | 23.4 | 25.2 | 26.8 |
| ρ = 0.5 ρb | 17.4 | 19.2 | 20.7 | 22.0 | 18.4 | 20.2 | 21.8 | 23.1 | 19.1 | 21.0 | 22.6 | 24.0 | 19.7 | 21.7 | 23.3 | 24.8 | 20.9 | 23.0 | 24.7 | 26.3 | 22.0 | 24.2 | 26.0 | 27.7 |
| ρ = ρmax = 0.634ρb | 17.6 | 19.3 | 20.8 | 22.1 | 18.5 | 20.4 | 22.0 | 23.3 | 19.2 | 21.2 | 22.8 | 24.2 | 19.7 | 21.7 | 23.4 | 24.9 | 21.1 | 23.2 | 25.0 | 26.5 | 22.2 | 24.4 | 26.3 | 28.0 |
| ρ = ρt = 0.724ρb | 17.7 | 19.4 | 20.9 | 22.2 | 18.6 | 20.5 | 22.1 | 23.5 | 19.3 | 21.3 | 22.9 | 24.4 | 19.8 | 21.8 | 23.5 | 25.0 | 21.2 | 23.3 | 25.1 | 26.7 | 22.3 | 24.6 | 26.4 | 28.1 |
| ρ = ρb | 17.9 | 19.7 | 21.2 | 22.5 | 18.9 | 20.8 | 22.4 | 23.8 | 19.6 | 21.6 | 23.3 | 24.7 | 20.3 | 22.3 | 24.0 | 25.5 | 21.4 | 23.5 | 25.3 | 26.9 | 22.5 | 24.8 | 26.7 | 28.4 |
| Avg. = | 17.5 | 19.3 | 20.7 | 22.0 | 18.4 | 20.3 | 21.8 | 23.2 | 19.1 | 21.1 | 22.7 | 24.1 | 19.7 | 21.7 | 23.4 | 24.8 | 21.0 | 23.1 | 24.8 | 26.4 | 22.1 | 24.3 | 26.1 | 27.8 |
| - | w = "3 kips/ft = 4.08 kN/m" | |||||||||||||||||||||||
| ρ = 0 | 14.7 | 16.2 | 17.5 | 18.6 | 15.5 | 17.0 | 18.3 | 19.5 | 16.1 | 17.7 | 19.0 | 20.2 | 16.6 | 18.2 | 19.6 | 20.9 | 17.7 | 19.5 | 21.0 | 22.3 | 18.6 | 20.5 | 22.0 | 23.4 |
| ρ = 0.5 ρb | 15.2 | 16.8 | 18.1 | 19.2 | 16.0 | 17.7 | 19.0 | 20.2 | 16.7 | 18.3 | 19.8 | 21.0 | 17.2 | 18.9 | 20.4 | 21.7 | 18.2 | 20.1 | 21.6 | 23.0 | 19.2 | 21.1 | 22.7 | 24.2 |
| ρ = ρmax = 0.634ρb | 15.4 | 16.9 | 18.2 | 19.3 | 16.2 | 17.8 | 19.2 | 20.4 | 16.8 | 18.5 | 19.9 | 21.2 | 17.3 | 19.0 | 20.5 | 21.7 | 18.4 | 20.3 | 21.8 | 23.2 | 19.4 | 21.3 | 23.0 | 24.4 |
| ρ = ρt = 0.724ρb | 15.4 | 17.0 | 18.3 | 19.4 | 16.3 | 17.9 | 19.3 | 20.5 | 16.9 | 18.6 | 20.0 | 21.3 | 17.3 | 19.1 | 20.6 | 21.8 | 18.5 | 20.4 | 21.9 | 23.3 | 19.5 | 21.4 | 23.1 | 24.6 |
| ρ = ρb | 15.6 | 17.2 | 18.5 | 19.7 | 16.5 | 18.2 | 19.6 | 20.8 | 17.1 | 18.9 | 20.3 | 21.6 | 17.7 | 19.5 | 21.0 | 22.3 | 18.7 | 20.5 | 22.1 | 23.5 | 19.7 | 21.7 | 23.3 | 24.8 |
| Avg. = | 15.3 | 16.8 | 18.1 | 19.3 | 16.1 | 17.7 | 19.1 | 20.3 | 16.7 | 18.4 | 19.8 | 21.1 | 17.2 | 18.9 | 20.4 | 21.7 | 18.3 | 20.1 | 21.7 | 23.1 | 19.3 | 21.2 | 22.8 | 24.3 |
| - | w = "4 kips/ft = 58.4 kN/m" | |||||||||||||||||||||||
| ρ = 0 | 13.4 | 14.7 | 15.9 | 16.9 | 14.1 | 15.5 | 16.7 | 17.7 | 14.6 | 16.1 | 17.3 | 18.4 | 15.0 | 16.6 | 17.8 | 19.0 | 16.1 | 17.7 | 19.1 | 20.3 | 16.9 | 18.6 | 20.0 | 21.3 |
| ρ = 0.5 ρb | 13.8 | 15.2 | 16.4 | 17.4 | 14.6 | 16.0 | 17.3 | 18.4 | 15.1 | 16.7 | 18.0 | 19.1 | 15.6 | 17.2 | 18.5 | 19.7 | 16.6 | 18.2 | 19.6 | 20.9 | 17.4 | 19.2 | 20.7 | 22.0 |
| ρ = ρmax = 0.634ρb | 13.9 | 15.4 | 16.5 | 17.6 | 14.7 | 16.2 | 17.4 | 18.5 | 15.3 | 16.8 | 18.1 | 19.2 | 15.7 | 17.3 | 18.6 | 19.7 | 16.7 | 18.4 | 19.8 | 21.1 | 17.6 | 19.4 | 20.9 | 22.2 |
| ρ = ρt = 0.724ρb | 14.0 | 15.4 | 16.6 | 17.7 | 14.8 | 16.3 | 17.5 | 18.6 | 15.3 | 16.9 | 18.2 | 19.3 | 15.8 | 17.3 | 18.7 | 19.8 | 16.8 | 18.5 | 19.9 | 21.2 | 17.7 | 19.5 | 21.0 | 22.3 |
| ρ = ρb | 14.2 | 15.6 | 16.8 | 17.9 | 15.0 | 16.5 | 17.8 | 18.9 | 15.6 | 17.1 | 18.5 | 19.6 | 16.1 | 17.7 | 19.1 | 20.3 | 17.0 | 18.7 | 20.1 | 21.4 | 17.9 | 19.7 | 21.2 | 22.5 |
| Avg. = | 13.9 | 15.3 | 16.5 | 17.5 | 14.6 | 16.1 | 17.3 | 18.4 | 15.2 | 16.7 | 18.0 | 19.1 | 15.6 | 17.2 | 18.5 | 19.7 | 16.6 | 18.3 | 19.7 | 21.0 | 17.5 | 19.3 | 20.8 | 22.1 |
| α = 0.0054 | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| - | fc' = 3000 (psi) = 21 (MPa) | fc' = 4000 (psi) = 28 (MPa) | fc' = 5000 (psi) = 35 (MPa) | fc' = 6000 (psi) = 42 (MPa) | fc' = 9000 (psi) = 63 (MPa) | fc' = 12000 (psi) = 84 (MPa) | ||||||||||||||||||
| b (in) | 6 | 8 | 10 | 12 | 6 | 8 | 10 | 12 | 6 | 8 | 10 | 12 | 6 | 8 | 10 | 12 | 6 | 8 | 10 | 12 | 6 | 8 | 10 | 12 |
| b (mm) | 150 | 200 | 250 | 300 | 150 | 200 | 250 | 300 | 150 | 200 | 250 | 300 | 150 | 200 | 250 | 300 | 150 | 200 | 250 | 300 | 150 | 200 | 250 | 300 |
| - | w = "1 kips/ft = 14.6 kN/m" | |||||||||||||||||||||||
| ρ = 0 | 7.5 | 8.2 | 8.9 | 9.4 | 7.8 | 8.6 | 9.3 | 9.9 | 8.1 | 8.9 | 9.6 | 10.2 | 8.4 | 9.2 | 9.9 | 10.6 | 9.0 | 9.9 | 10.6 | 11.3 | 9.4 | 10.4 | 11.2 | 11.9 |
| ρ = 0.5 ρb | 7.7 | 8.5 | 9.1 | 9.7 | 8.1 | 8.9 | 9.6 | 10.2 | 8.4 | 9.3 | 10.0 | 10.6 | 8.7 | 9.6 | 10.3 | 11.0 | 9.2 | 10.2 | 10.9 | 11.6 | 9.7 | 10.7 | 11.5 | 12.2 |
| ρ = ρmax = 0.634ρb | 7.8 | 8.6 | 9.2 | 9.8 | 8.2 | 9.0 | 9.7 | 10.3 | 8.5 | 9.4 | 10.1 | 10.7 | 8.7 | 9.6 | 10.4 | 11.0 | 9.3 | 10.3 | 11.0 | 11.7 | 9.8 | 10.8 | 11.6 | 12.4 |
| ρ = ρt = 0.724ρb | 7.8 | 8.6 | 9.3 | 9.8 | 8.2 | 9.1 | 9.8 | 10.4 | 8.5 | 9.4 | 10.1 | 10.8 | 8.8 | 9.7 | 10.4 | 11.1 | 9.4 | 10.3 | 11.1 | 11.8 | 9.9 | 10.9 | 11.7 | 12.4 |
| ρ = ρb | 7.9 | 8.7 | 9.4 | 10.0 | 8.4 | 9.2 | 9.9 | 10.5 | 8.7 | 9.5 | 10.3 | 10.9 | 9.0 | 9.9 | 10.6 | 11.3 | 9.4 | 10.4 | 11.2 | 11.9 | 10.0 | 11.0 | 11.8 | 12.5 |
| Avg. = | 7.7 | 8.5 | 9.2 | 9.7 | 8.1 | 9.0 | 9.7 | 10.3 | 8.5 | 9.3 | 10.0 | 10.7 | 8.7 | 9.6 | 10.3 | 11.0 | 9.3 | 10.2 | 11.0 | 11.7 | 9.8 | 10.7 | 11.6 | 12.3 |
| - | w = "2 kips/ft = 29.2 kN/m" | |||||||||||||||||||||||
| ρ = 0 | 5.9 | 6.5 | 7.0 | 7.5 | 6.2 | 6.8 | 7.4 | 7.8 | 6.5 | 7.1 | 7.7 | 8.1 | 6.7 | 7.3 | 7.9 | 8.4 | 7.1 | 7.8 | 8.4 | 9.0 | 7.5 | 8.2 | 8.9 | 9.4 |
| ρ = 0.5 ρb | 6.1 | 6.7 | 7.3 | 7.7 | 6.4 | 7.1 | 7.6 | 8.1 | 6.7 | 7.4 | 7.9 | 8.4 | 6.9 | 7.6 | 8.2 | 8.7 | 7.3 | 8.1 | 8.7 | 9.2 | 7.7 | 8.5 | 9.1 | 9.7 |
| ρ = ρmax = 0.634ρb | 6.2 | 6.8 | 7.3 | 7.8 | 6.5 | 7.2 | 7.7 | 8.2 | 6.8 | 7.4 | 8.0 | 8.5 | 6.9 | 7.6 | 8.2 | 8.7 | 7.4 | 8.1 | 8.8 | 9.3 | 7.8 | 8.6 | 9.2 | 9.8 |
| ρ = ρt = 0.724ρb | 6.2 | 6.8 | 7.3 | 7.8 | 6.5 | 7.2 | 7.7 | 8.2 | 6.8 | 7.5 | 8.0 | 8.5 | 7.0 | 7.7 | 8.3 | 8.8 | 7.4 | 8.2 | 8.8 | 9.4 | 7.8 | 8.6 | 9.3 | 9.9 |
| ρ = ρb | 6.3 | 6.9 | 7.4 | 7.9 | 6.6 | 7.3 | 7.9 | 8.4 | 6.9 | 7.6 | 8.2 | 8.7 | 7.1 | 7.8 | 8.4 | 9.0 | 7.5 | 8.3 | 8.9 | 9.4 | 7.9 | 8.7 | 9.4 | 10.0 |
| Avg. = | 6.1 | 6.8 | 7.3 | 7.7 | 6.5 | 7.1 | 7.7 | 8.1 | 6.7 | 7.4 | 8.0 | 8.5 | 6.9 | 7.6 | 8.2 | 8.7 | 7.4 | 8.1 | 8.7 | 9.3 | 7.7 | 8.5 | 9.2 | 9.8 |
| - | w = "3 kips/ft = 4.08 kN/m" | |||||||||||||||||||||||
| ρ = 0 | 5.2 | 5.7 | 6.1 | 6.5 | 5.4 | 6.0 | 6.4 | 6.8 | 5.6 | 6.2 | 6.7 | 7.1 | 5.8 | 6.4 | 6.9 | 7.3 | 6.2 | 6.8 | 7.4 | 7.8 | 6.5 | 7.2 | 7.7 | 8.2 |
| ρ = 0.5 ρb | 5.3 | 5.9 | 6.3 | 6.7 | 5.6 | 6.2 | 6.7 | 7.1 | 5.9 | 6.4 | 6.9 | 7.4 | 6.0 | 6.6 | 7.2 | 7.6 | 6.4 | 7.0 | 7.6 | 8.1 | 6.7 | 7.4 | 8.0 | 8.5 |
| ρ = ρmax = 0.634ρb | 5.4 | 5.9 | 6.4 | 6.8 | 5.7 | 6.3 | 6.7 | 7.2 | 5.9 | 6.5 | 7.0 | 7.4 | 6.1 | 6.7 | 7.2 | 7.6 | 6.5 | 7.1 | 7.7 | 8.1 | 6.8 | 7.5 | 8.1 | 8.6 |
| ρ = ρt = 0.724ρb | 5.4 | 6.0 | 6.4 | 6.8 | 5.7 | 6.3 | 6.8 | 7.2 | 5.9 | 6.5 | 7.0 | 7.5 | 6.1 | 6.7 | 7.2 | 7.7 | 6.5 | 7.1 | 7.7 | 8.2 | 6.8 | 7.5 | 8.1 | 8.6 |
| ρ = ρb | 5.5 | 6.0 | 6.5 | 6.9 | 5.8 | 6.4 | 6.9 | 7.3 | 6.0 | 6.6 | 7.1 | 7.6 | 6.2 | 6.8 | 7.4 | 7.8 | 6.6 | 7.2 | 7.8 | 8.3 | 6.9 | 7.6 | 8.2 | 8.7 |
| Avg. = | 5.4 | 5.9 | 6.4 | 6.8 | 5.6 | 6.2 | 6.7 | 7.1 | 5.9 | 6.5 | 7.0 | 7.4 | 6.0 | 6.6 | 7.2 | 7.6 | 6.4 | 7.1 | 7.6 | 8.1 | 6.8 | 7.4 | 8.0 | 8.5 |
| - | w = "4 kips/ft = 58.4 kN/m" | |||||||||||||||||||||||
| ρ = 0 | 4.7 | 5.2 | 5.6 | 5.9 | 4.9 | 5.4 | 5.9 | 6.2 | 5.1 | 5.6 | 6.1 | 6.5 | 5.3 | 5.8 | 6.3 | 6.7 | 5.6 | 6.2 | 6.7 | 7.1 | 5.9 | 6.5 | 7.0 | 7.5 |
| ρ = 0.5 ρb | 4.9 | 5.3 | 5.8 | 6.1 | 5.1 | 5.6 | 6.1 | 6.4 | 5.3 | 5.9 | 6.3 | 6.7 | 5.5 | 6.0 | 6.5 | 6.9 | 5.8 | 6.4 | 6.9 | 7.3 | 6.1 | 6.7 | 7.3 | 7.7 |
| ρ = ρmax = 0.634ρb | 4.9 | 5.4 | 5.8 | 6.2 | 5.2 | 5.7 | 6.1 | 6.5 | 5.4 | 5.9 | 6.4 | 6.8 | 5.5 | 6.1 | 6.5 | 6.9 | 5.9 | 6.5 | 7.0 | 7.4 | 6.2 | 6.8 | 7.3 | 7.8 |
| ρ = ρt = 0.724ρb | 4.9 | 5.4 | 5.8 | 6.2 | 5.2 | 5.7 | 6.2 | 6.5 | 5.4 | 5.9 | 6.4 | 6.8 | 5.5 | 6.1 | 6.6 | 7.0 | 5.9 | 6.5 | 7.0 | 7.4 | 6.2 | 6.8 | 7.4 | 7.8 |
| ρ = ρb | 5.0 | 5.5 | 5.9 | 6.3 | 5.3 | 5.8 | 6.2 | 6.6 | 5.5 | 6.0 | 6.5 | 6.9 | 5.6 | 6.2 | 6.7 | 7.1 | 6.0 | 6.6 | 7.1 | 7.5 | 6.3 | 6.9 | 7.4 | 7.9 |
| Avg. = | 4.9 | 5.4 | 5.8 | 6.1 | 5.1 | 5.6 | 6.1 | 6.5 | 5.3 | 5.9 | 6.3 | 6.7 | 5.5 | 6.0 | 6.5 | 6.9 | 5.8 | 6.4 | 6.9 | 7.4 | 6.1 | 6.8 | 7.3 | 7.7 |
3. RESULTS AND DISCUSSION
Fig. (1) shows the effect of the ratio of (ρ/ρb) on the span-depth ratio (N = L / h) for simply supported beam. The value of (N) increased linearly at a low rate, or in other words, the effect of (ρ/ρb) was small on the ratio (N), which also increased with increasing the width of the section (b). The same conclusions were obtained for other values of (fc' ) concrete compressive strength and applied load (w), because when reinforcement area is increased, we need smaller equivalent thickness to give the same moment of inertia, that is why the value of (N) is increased.
Fig. (2) shows the effect of the applied load (w) on the ratio (N) for simply supported beam. As shown, the value of (N) decreased with increasing the applied load (w); this means that the required depth increased with increasing the applied load value. The same conclusions were obtained for other values of (ρ / ρb = 0, 0.5 and 1.0). Also the behavior was same for other values of (ƒ'c and b).
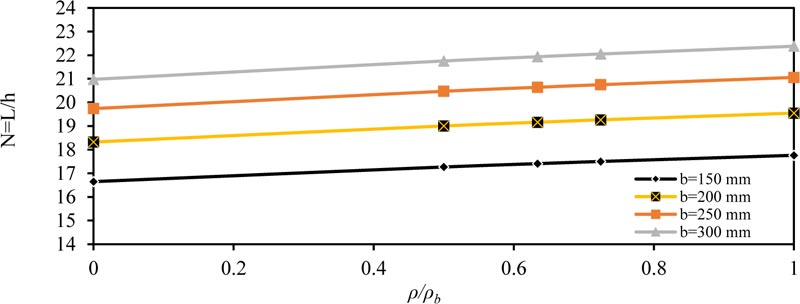 |
Fig. (1). Minimum thickness ratio (N = L / h) versus reinforcement ratio (ρ/ρb) for simply supported member (=28 MPa) and (w =14.6 kN/m). |
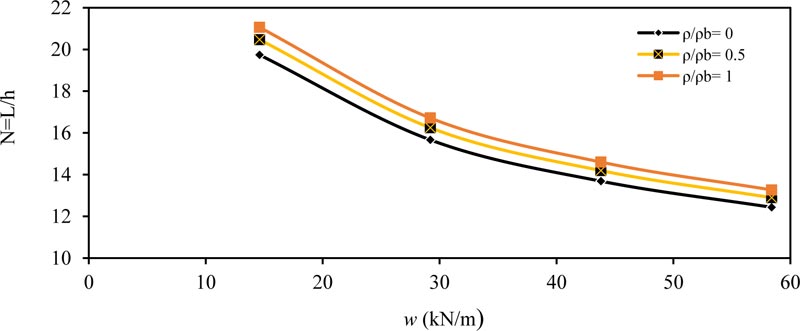 |
Fig. (2). Minimum thickness ratio (N = L / h) versus load w (kN/m) for simply supported member (=28 MPa) and (b = 250 mm). |
Fig. (3) shows the effect of concrete compressive strength (fc' ) on (N) for the simply supported beam for (ρ / ρb= 0, 0.5 and 1.0). As shown, the value of (N) increased with increasing (fc' ) because as the concrete became more robust, the modulus of elasticity increased. Therefore, we need smaller equivalent depth to obtain the same maximum deflection within the ACI-maximum deflection limit. The same behavior is obtained for other values of applied load (w) and cross-section depth (b), as shown in Tables 4-7. Also, when the cross-section width b is increased, the value of (N) also increases, that is, smaller depth is required to obtain the same moment of inertia and same maximum deflection within the ACI-limit.
The same behavior and conclusions are obtained in other type of beams, as shown in Figs. (4-6) for fixed ended beam, Figs. (7-9) for propped beam and Figs. (10-12) for a cantilever beam.
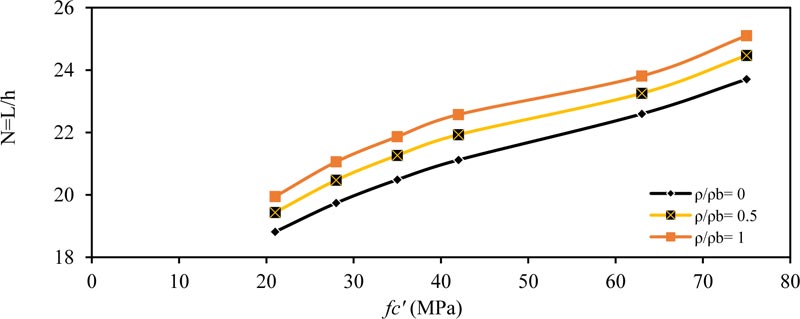 |
Fig. (3). Minimum thickness ratio (N = L / h) versus compressive strength (MPa) for simply supported member (w =14.6 kN/m) and (b = 250 mm). |
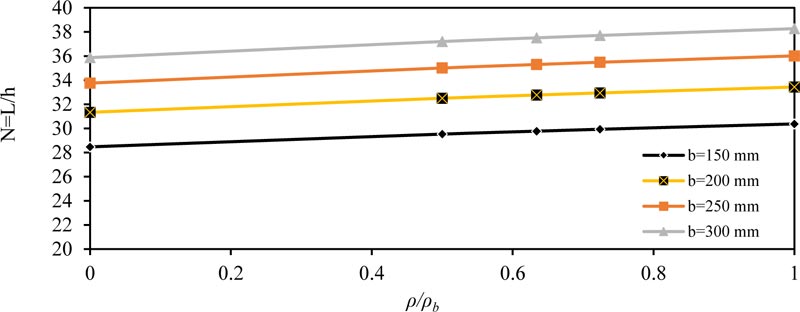 |
Fig. (4). Minimum thickness ratio (N = L / h) versus reinforcement ratio (ρ/ρb) for fixed ended member (=28 MPa) and (w =14.6 kN/m). |
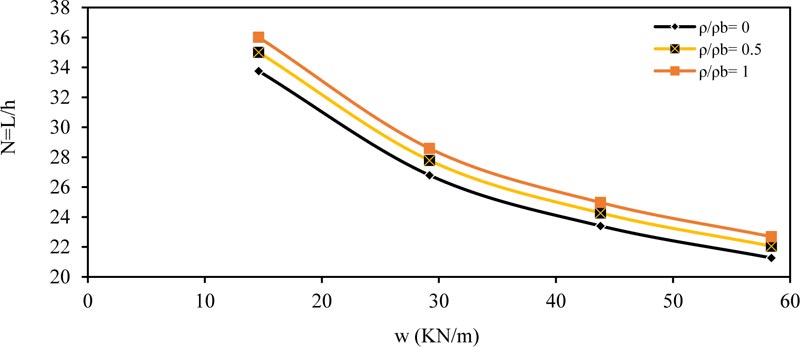 |
Fig. (5). Minimum thickness ratio (N = L / h) versus load w (kN/m) for fixed ended member (=28 MPa) and (b = 250 mm). |
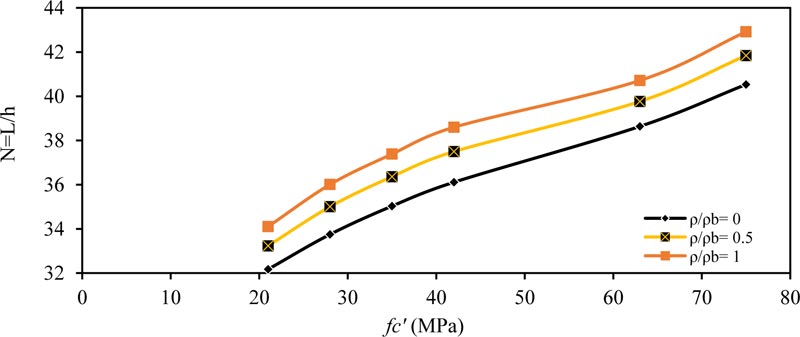 |
Fig. (6). Minimum thickness ratio (N = L / h) versus compressive strength fc'(MPa) for fixed ended member (w =14.6 kN/m) and (b = 250 mm). |
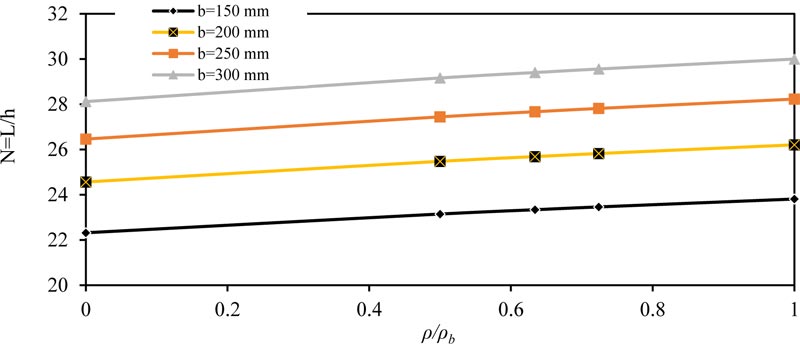 |
Fig. (7). Minimum thickness ratio (N = L / h) versus reinforcement ratio (ρ/ρb) for propped member (fc' =28 MPa) and (w =14.6 kN/m). |
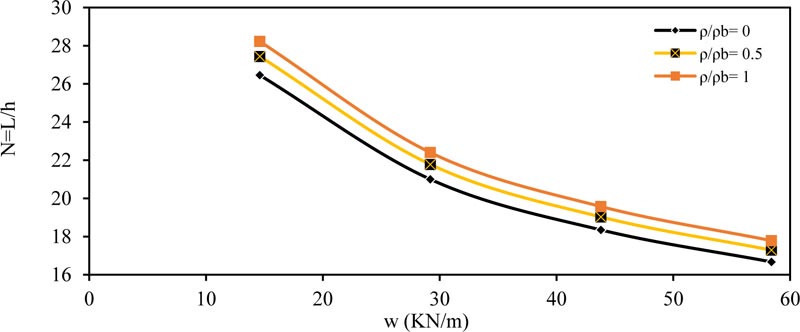 |
Fig. (8). Minimum thickness ratio (N = L / h) versus load w (kN/m) for propped member (fc' =28 MPa) and (b = 250 mm). |
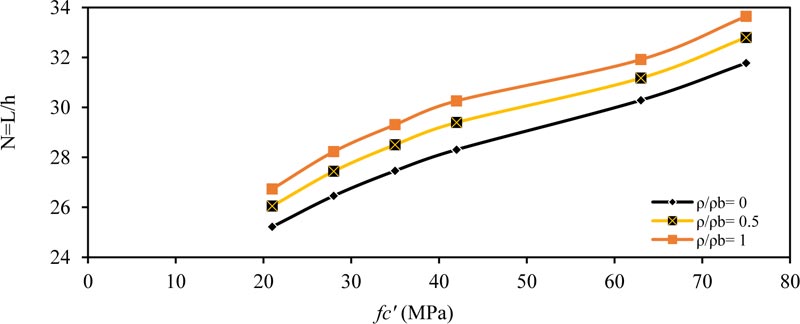 |
Fig. (9). Minimum thickness ratio (N = L / h) versus compressive strength fc'(MPa) for propped member (w =14.6 kN/m) and (b = 250 mm). |
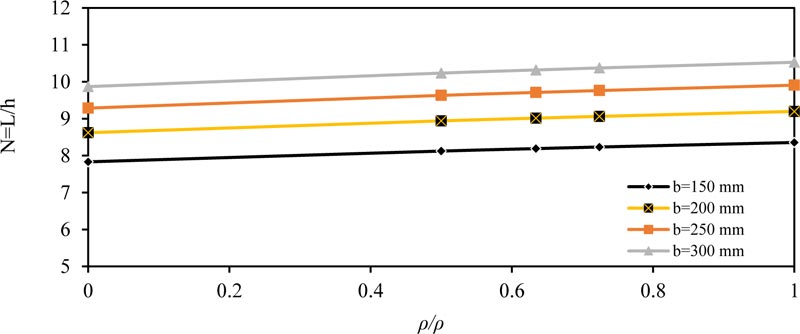 |
Fig. (10). Minimum thickness ratio (N = L / h) versus reinforcement ratio (ρ/ρb) for cantilever member (fc' =28 MPa) and (w =14.6 kN/m). |
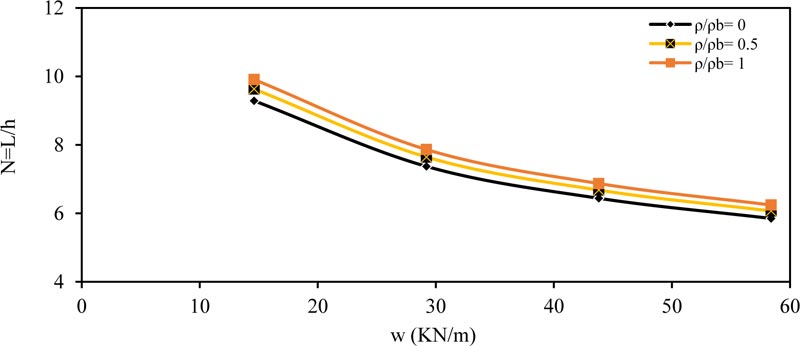 |
Fig. (11). Minimum thickness ratio (N = L / h) versus load w (kN/m) for cantilever member (fc' =28 MPa) and (b = 250 mm). |
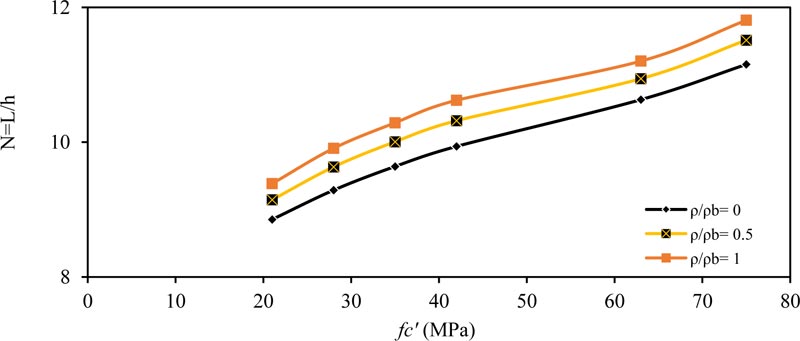 |
Fig. (12). Minimum thickness ratio (N = L / h) versus compressive strength fc'(MPa) for cantilever member (w =14.6 kN/m) and (b = 250 mm). |
CONCLUSION
- 1- A modification of ACI code span-depth ratio is suggested to include the effect of tension reinforcement area, which is represented by the reinforcement indices ratio (ρ/ρb), applied distributed load (w), concrete compressive strength (fc' ) and cross section width (b) in order to control the maximum deflection of the beam within the ACI limit of the maximum permitted deflection.
- 2- The value of span-depth ratio (N = L / h) is determined for four beam types (simply supported, fixed ended, propped and cantilever) for concrete strengths (ƒ'c = 21, 28, 35, 42, 63 & 84 MPa), applied distributed load (w = 14.6, 29.2, 43.8 & 58.4 kN/m), cross width (b = 150, 200, 250 & 300 mm) and (ρ / ρb = 0, 0.5 & 1) in addition to (ρt /ρb & ρmax /ρb).
- 3- The effect of the reinforced indicia ratio (ρ/ρb) is small on the span-depth ratio (N = L / h) for all values of applied load and concrete compressive strength.
- 4- The span-depth ratio (N = L / h) decreased with increasing the applied load, or in other words, the required depth increased with increasing the applied load for all values of concrete strength and beam width.
- 5- The span-depth ratio (N = L / h) increased with increasing the concrete strength (fc' ), i.e. the required depth decreased with increasing concrete strength for all values of applied loads and beam width.
- 6- The same behavior and conclusions were obtained for all types (simply supported, fixed ended, propped and cantilever).
- 7- Different numerical examples are solved to verify the results of the proposed equations and tables for all types of beams (simply supported, fixed ended, propped and cantilever).
- 8- For a simply supported beam with an amount of reinforcement equal to balance ratio (ρ = ρb), the equivalent depth is reduced by (6.23%) to provide the same deflection within the maximum permissible limit (L/360).
- 9- For a fixed ended beam with an amount of reinforcement equal to half of the balance ratio (ρ = ρb), the equivalent depth is reduced by (3.66%) to provide the same deflection within the maximum permissible limit (L/360).
- 10- For propped beam (one end is simply supported and the other end is fixed) with an amount of reinforcement equal to balance ratio (ρ = ρb), the equivalent depth is reduced by (6.44%) to provide the same deflection within the maximum permissible limit (L/360).
- 11- For a cantilever beam with an amount of reinforcement equal to the balance ratio (ρ = ρb), the equivalent depth is reduced by (6.267%) to provide the same deflection within the maximum permissible limit (L/360).
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
Not applicable.
FUNDING
None.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.







