All published articles of this journal are available on ScienceDirect.
Stability Assessment of Diaphram Cellular Cofferdams Subjected to Severe Hydro-structural Conditions
Abstract
Background:
Cellular cofferdams are a temporary construction consisting of interlocking steel sheet pilings driven into the ground as a series of interconnecting cells.
Objectives:
This study aims to investigate the stability of cofferdams with a circular diaphragm due to lateral load in dry and wet soil cases.
Discussion:
A series of laboratory tests were performed on different width to height ratios (0.8, 0.9, and 1.0), berm ratios (0.2H, 0.3H, and 0.4H), and embedment depth ratios (0.2H, 0.3H, and 0.4H) with four types of soil fill (clay soil, river sand, sand passing sieve No.4, and sub base).
The coupled circular cofferdam-soil system was modelled using nonlinear finite element analysis (COMSOL Multiphysics Software) to validate the experimental results.
Conclusion:
After applying hydrostatic, hydrodynamic, and structural failure loads, the resistance of the cellular retaining structures with wet soil fill in saturated soils was greater than with dry soil fill in dry soils. The most advantageous construction format was found by deciphering the relationship between the aforementioned loads and berm ratios, embedment depth, and horizontal displacement.
1. INTRODUCTION
It is complicated and difficult to construct the offshore foundation of a bridge pier because of the cofferdam installation, which causes an increase in the construction costs and time as compared to an onshore foundation of a pier. A conventional steel cofferdam has common configurations such as circular, diaphragm, and cloverleaf to exclude water during excavation and ensure construction in dry conditions [1]. A steel cofferdam is built by assembling many pieces of flat or circular web sheet piles to interlock with each other. Frequent pauses and accidents during this process are expected due to weather conditions and worker’s mistakes. To overcome these difficulties, a large circular mono-cofferdam is examined for application as an alternative to assembled sheet piles (Fig. 1).
Cofferdams are exposed to ocean waves and hydrostatic pressures. In particular, due to their large dimensions, high hydrodynamic pressures are expected which increases construction costs. This weakens the relative advantage of the cofferdam. They are also used as permanent structures to retain water, for which higher structural safety requirements are needed. Furthermore, loads such as water current and waves cause a large amount of motion in a cofferdam during installation and result in limiting their utility. Thus, solutions to these above challenges for cofferdams are needed. The resisting forces towards the sliding and overturning range are soil to soil depending on the unit weight, the coefficient of friction of the soil, young’s modulus of elasticity, poison’s ratio, and cohesion [2].
The design and construction of cellular cofferdams through test models to observe their stability has been studied by Rossow and his colleague [3]. Koltuk et al. studied the behaviour of a double sheet pile wall cofferdam on a thick clay deposit that was known to produce flash floods. A series of centrifuge version tests were performed to check outcomes. The consolidation of the clay foundation impacted the steadiness of the cofferdam through various degrees of consolidation [4]. The four types of soil used were subbase, sand passing sieve No.4, river sand, and clay.
Amin Khan et al [5] studied the behaviour of a double sheet pile wall cofferdam on sandy soil subjected to a high level of water. The test results implied that: (i) the shear deformation of the fill dominated the failure mechanism of the cofferdam, (ii) as the width of the cofferdam increases, the water height at failure increases, and (iii) the sheet pile wall downstream is subjected to higher stresses than the sheet pile wall upstream.Based on hydraulic computation theory, a hydraulic numerical model was built describing an overflow cofferdam during the multi-phase diversion. This determined the discharge capacities, stream water levels, and the velocities of both the overflowed cofferdam and narrowed river [6]. The calculated values of this model are in good agreement with the observed data.
The design and construction of cellular cofferdams using test models to observe their stability have been studied [7]. A series of laboratory tests were performed on two diaphragm cells of different width to depth ratios (0.75, 0.85, and 1). Then, the cellular cofferdam was analysed by PLAXIS software which is used to compute deformations, stresses, and strain in the body of cofferdams and foundations. The functions represent the relation between deformations and embedment depths that occurred after applied loads. Many conclusions have been drawn from this study; one of which is that embedment depth greatly affects the resistance and deformation of the cell. AL-Khyatt [8] studied the stability of cellular cofferdams through testing the models of three cases of isolated circular cofferdams with different cell width (b) to cell height (H) ratio (b/H) and five types of soil fill. The results of the tests indicated that the cells filled with sub-base were more stable against sliding at different (b/H) ratios and the cells filled with sand passing No.8 were more stable against overturning at different (b/H) ratios. A study presented nonlinear finite element analysis used to predict the load deflection behaviour of a circular cell cofferdam under lateral load by using ANSYS (version 5.4) [9]. The full Newton-Raphson method was used for the nonlinear solution algorithm.
The effect of berm and embedment depth on the stability of cofferdams in wet soils has been studied [10]. The research showed that the resistance of the cellular retaining structure (cofferdam) with wet soils in wet foundations gives greater resistance than in dry soils, while another study [11] presents the study of nonlinear finite element analysis predicting the load deflection behaviour of the cellular cell cofferdam under lateral load by using ANSYS (version 12.1) computer program.
The stability of cloverleaf cofferdams in two soil cases (dry and wet) and two positions (neutral and longitudinal), with nonlinear finite elements to predict the load-deflection behaviour of cellular cell cofferdams under lateral load, was analysed. The results expressed that the cells filled with wet sub-base were more stable against sliding and overturning at different (b/H) ratios, and the cells that had longitudinal direction were more stable against sliding and overturning at different (b/H) ratios as compared to the cells with neutral direction. The purpose of a cofferdam is to allow for the removal of soil and/or water from an area in which construction work is to be carried out below the surface [12, 13]. The use of cellular bulkheads as permanent retaining structures developed directly from cofferdam construction. A bulkhead is primarily intended to retain or prevent sliding of the land while protecting the upland area against wave action is of secondary importance. The cellular structure has been constructed in a variety of geometric shapes, the three most common shapes being circular, diaphragm, and cloverleaf [14]. A series of laboratory tests were carried out on one (single) diaphragm cell of different width to height ratios, and the results obtained from this research indicated that the embedment depth ratio gave a greater resistance for cell than the berm ratio [15].
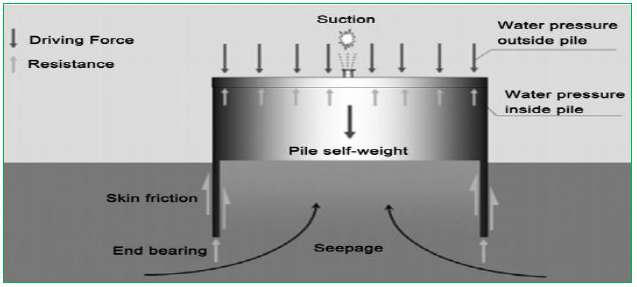
The foundation of the dam is important for its stability. The quaternary layer can consist of a variety of soil types. It is beneficial to build an offshore structure like an atoll on a sandbank because of the more shallow water. Because of this, the top layer will consist of sand. Investigations done by several authors illustrate the soil layer characteristics [16-22].
Various researchers have studied the stability of cofferdams by using finite elements software and the results are quite comprehensive [23-26]. present data on the forces surrounding cofferdams and the stability criteria of the various types of cofferdams according to different codes. In these studies a circular cellular sheet pile cofferdam was chosen because it can be used singularly in a group, it will not collapse in the event of failure of the adjoining cells, each cell acts independently of the other, and it requires fewer sheet piles. Both the conventional method and the finite element method give good results with a small margin of error.
Several studies were conducted to improve the structural performance of the cofferdam concerning design and construction. Mahan [27] presented theoretical methods for the design of cellular sheet pile cofferdams and established design procedures. Iqbal [28] conducted a finite element analysis of cellular cofferdams to determine the interlocking tension in the sheet piles subjected to wave loads after construction and verified the results of this analysis by comparing it to the recorded data. Sheppard [29] investigated soil-structure interaction effects on sheet pile tensions using finite element analyses. Although this research showed important considerations of cofferdam design, the cofferdam types were restricted to cellular types using sheet pile. More recently, prefabricated types of cofferdams have been proposed and studied. Mosher [30] introduced a huge double-wall steel boxed cofferdam applied to main bridge pier construction.
Cellular cofferdams have been very rarely utilized as the main permanent structure for hydropower dams. Consequently, design and construction requirements for cellular cofferdams are less stringent than for hydropower dams [31-35]. explain notable examples of successful uses of cellular cofferdams with circular-type cells and connecting cells. Spatially, this type was used for the majority of subsequent cofferdam constructions. However, as mentioned in [36-39], efforts to quantify the economic impacts on water resources are hampered by the fact that the estimates are highly sensitive to different estimation methods and to different assumptions regarding how changes in water availability will be allocated across various types of water uses such as agricultural, urban, or in-stream uses. The overtopping flow can cause hydro-dynamic forces to act on the rock fill part in the downstream berm, dragging the rock fill materials and causing instability to the entire cofferdam [40]. Overtopping failures due to erosion or piping account for more than 30% of dam failures [41-44] with a simple assumption of simplicity in geometry, material behaviour, or dynamic loading to make the equations solvable [45].
One of the biggest contributors to the cost of cofferdams is in-water construction problems, which emphasizes the important advantages of cellular cofferdams [46–57]. Also, the sheet pile driven into the soil has numerous mechanical properties that can affect the cofferdam’s performance [58-62].
Saba’a and AL-humairi [63] used nonlinear finite element analysis to predict the load displacement behaviour of cellular retaining structures by using the ANSYS (Analysis System, version 9) computer program. Eight-node brick element was used to model cellular cofferdams and soil. Nonlinear material behaviour is adopted for the soil and a Drucker-Prager (DP) model is used to represent that nonlinearity. The results are compared with experimental data [8] as well as with the results of [64, 65] with good agreement.
Nakasone et al, [66] presents the results of a comprehensive study on the potential use of cellular cofferdams as a basis for the design and construction of water retaining structures to sustainably and cost-effectively harness hydropower. The results show cellular cofferdams have the potential to be used as a foundation for the construction of permanent hydropower dam structures that are versatile with less impact on the environment and that will cost less to build than conventional hydropower dams. According to the research conducted by the Oak Ridge National Lab [67], even though 2,200 hydropower plants have been in use to supply about 7% (80 GW) of all U.S. power generating needs, there remains up to 60 GW of untapped hydropower potential that can be developed. Bang and Cho [68] believed that the strength of even ground is linearly increasing with the depth of soft clay ground and un-drained horizontal bearing capacity can be solved using the ultimate equilibrium method. Xue [69] discussed three failure modes and the corresponding calculation methods of the ultimate withdrawal resistances of cylindrical foundations in clay ground. The stability of the anti-overturn was also performed according to the shallow foundation code. Zhang et al, [70] tested numerical simulation on the characteristics of bearing capacity for the suction caisson in saturated sand ground and analysed the influence of length-radius ratios on bearing capacity under different load-displacement curves and coupled loads.
Zdravkovic et al, [71] utilized a three-dimensional Fourier series aided by the finite element method to analyse the bearing capacity of the suction caisson in soft ground taking into consideration the influence of the loading direction, length-radius ratio, cohesive strength, and anisotropy of the soil. Supachawarote et al, [72] used the swipe method and displacement method to apply load on the suction caisson foundation and gave the failure enveloping surface of bearing capacity. Wang and Miao [73] determined slippage displacement and angle of rotation as the main referring parameters of the dynamic response using the finite element method and dynamic analysis method when the caisson-type breakwater is subjected to the dynamic wave load. The variation tendency of the slippage displacement and the rational angle along the time history was also proposed. Wang and Yu [74, 75] researched the deformation and stress under the interaction of the caisson, foundation, and rear filling and analysed the stress and settlement of the caisson using ANSYS under static conditions. Al-Taee and Al-Rammahi [76] analysed the retaining structure and the deformation that occurs in the body of the retaining structure after the applied failure load is detected by using the software PLAXIS. The failure loads were obtained from a series of laboratory tests, and the cofferdam was modelled by using finite element code PLAXIS.
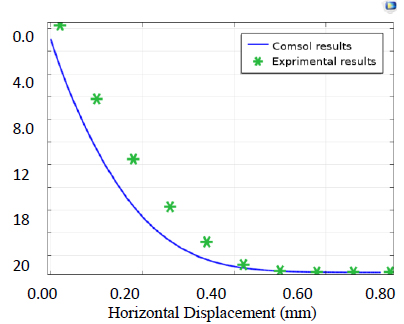
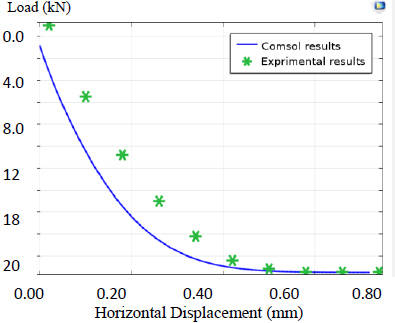
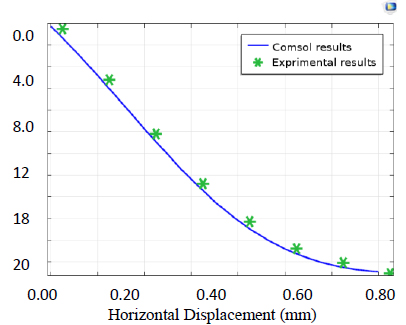
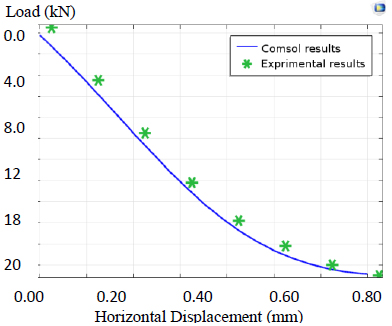
A series of laboratory tests have been carried out on circular diaphragm cells of different width to depth ratios. The tests included a study of the effects of height, width, length, embedment depth, and hydro-structural loading. Then, analysis of the cellular cofferdam by Comsol Software was performed to compute deformations, stresses, and strain in the body of the cofferdam and its foundation. A comparison of the results between the laboratory tests and the software results obtained from experimental tests by statistical analysis was created to compute the deformations.
2. MATERIALS AND METHODS
2.1. Experimental Work
In this paper, the effects of berm and embedment depth on the stability of cofferdams in saturated soils were studied. A series of laboratory tests were performed on one (single) circular and diaphragm cell with different width to height ratios. We used the trapezoidal berm of slope 1V:3H, where V: vertical and H: horizontal, with ratios of 0.2 and 0.4 from the height of the cell, and these were compared with the embedment depth case for ratios 0.2, 0.3, and 0.4 from the height of the cell for four types of soils (sub-base, sand passing on No. 4, river sand, and clay soil). This was to provide properties of soil that were free-draining and had a high angle of internal friction, غ. Table 1 explains the types and properties of the soils used in the cell fill and foundation.
In all tests, the soil bed was placed using a raining technique on a wooden box of 45 cm height. The raining technique has been used successfully in providing a uniformly dense soil bed for model studies. A height of 90 cm is kept between the sieve that is used in the raining technique and the top surface of the soil.
After that, water was added to the foundation soil by pipes supported at four sides until saturation of the soil was reached. The cells then were placed within the centre width of the soil field at 20 cm distance from the help of dial gauges.
A standard proctor test and direct shear test were executed for all soil types to find the maximum dry density and optimum water content. The field dry density was calculated by 80% of the maximum dry density. Then, the wetting unit weight was found. Next, we attempt to discover the attitude of inner friction (ø)º, and the fashions are filled with wet soil at 3 layers and compacted. The cell stage was checked through the accessible level and the loading system and dial gauges were adjusted. The burden was applied incrementally and continued until a failure in the model occurred (overturning of the cell). At the end of each load increment, the dial gauges were recorded. The horizontal displacements of the cell at each load level and increment were calculated. In all tests, the same soil type was used in the cell fill and foundation.
These tests were repeated with the other two cases. On each of these cells, the load is applied at one-third of the height (10 cm), so that the difference between sliding and overturning failure can easily be identified. The second case had a trapezoidal berm with a slope of 1V: 3H on the back side of the cells and with ratios of 0.2H, 0.3 and 0.4H from the height of the cells. In the last case, the cells were driven into the soil (embedment depth) for depth to height ratios of 0.2, 0.3, and 0.4. Fig. (1) illustrates the testing apparatus.
In all of the experimental tests, the soil filling the metallic field is compacted via vibrator to provide a uniformly dense soil bed for models used in the study [14]. Three types of soils were used inside the experimental checks. For each check, the equivalent type of soil is used as a cellular fill and base, and both dry and moist soils are used. Water content material, dry density, and direct shear measurements were calculated for all soil types and the wetting unit weight was determined. Next, we attempt to locate the attitude of internal friction (ø). The cloverleaf mobile model is filled with dry or wet soil at three layers and compacted carefully. It is located at the centre of the bases’ outbox. Three distinctive varieties of cloverleaf cells were tested. These varieties have a base width to height ratio (b/h) of 1.0, 0.9, and 0.8. All of the varieties of cells were examined by using three one of a kind vicinity heights from the bottom: 100 mm, 150 mm, and on the pinnacle factor model, 300 mm. Unique conditions for making use of masses, the primary carried out on two leaves and 50 mm top is mounted by using screws above the two sides of the container. There's one hollow in the middle of the beam to help metal screwed shaft, 1 mm diameter, and 800 mm length. The metallic shaft is used to support four dial gauges. These dial gauges, of 0.01 mm accuracy, are used to measure the displacement of the models throughout the entire testing program. Fig. (1) shows the scheme cell loading model used in this study.
| Type of Soil | Dry Density (γ) | Max. Dry Density(γmax) (kN/m3) | Optimum Water Content (%) | Angle of Friction (ø)º |
|---|---|---|---|---|
| Subbase | 17 | 21 | 10 | 38 |
| Sand passing on No.4 | 16.60 | 18.40 | 13.80 | 34 |
| River sand | 14.45 | 15.65 | 17.20 | 32 |
| clay soil | 12.25 | 13.75 | 19.25 | 29.45 |
2.2. Numerical Modelling
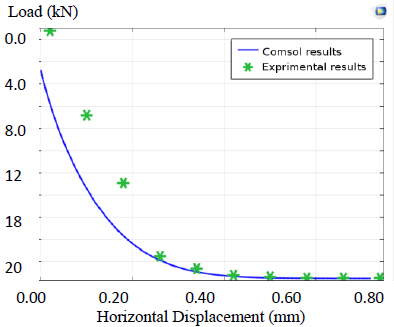
The COMSOL Analysis System computer program is a large-scale multiphysics finite element program used for solving several classes of engineering problems. The analysis capabilities of COMSOL include the ability to solve static and dynamic structural problems, steady-state and transient heat transfer problems, mode-frequency and buckling eigenvalue problems, static or time-varying magnetic analyses, and various types of field and coupled-field applications. The program contains many special features that allow nonlinearities or secondary effects to be included in the solution such as plasticity large strains, hyperelasticity, creep, swelling, large deflections, contact, stress stiffening, temperature dependency, material anisotropy, and radiation. Over time, other special capabilities such as sub-structuring, sub-modelling, random vibration, kinetostatics, kinetodynamics, free convection fluid analysis, acoustics, magnetics, piezoelectric, coupled-field analysis, and design optimization have been added to COMSOL. Nonlinear finite element evaluation has been used to predict the load deflection conduct of round cell cofferdams below lateral load via COMSOL version 5.4. There are three case studies (cofferdam with arcs and with arcs and backfilling, cofferdam with filling material different from the base of the dam, and cofferdam with soil layered filling). Three different sections of dams with diameter/depth (D/H) =1, 0.9, and 0.8 were analyzed in the first study, and the results were found to have good agreement with experimental data. The second study focused on an isolated cell cofferdam, and the last case study was a field study. Among the conclusions obtained from these studies, it was found that the stability of the dam increases with a decrease in the diameter (base) to height ratio of the dam. It was also found that there is a reduction in the displacement of the cofferdam by 82.58%, 89.24%, 5.1%, and 40.91%, respectively.
Singh [77] studied the design and production of mobile cofferdams via laboratory tests to review their balance. A series of laboratory tests were completed on diaphragm cells of different width to depth ratios (0.8, 0.9, and 1.0). The examinations focused on the impact of width, peak, properties of soil, and embedment depth to height ratios (0.2, 0.3, and 0.4). Four types of soil were used: sub-base, sand passing sieve no.4, river sand, and clay. The evaluation of cellular cofferdam via PLAXIS software program was performed to compute deformations, stresses, and strain inside the frame of cofferdam and foundation and for comparison to the laboratory results.
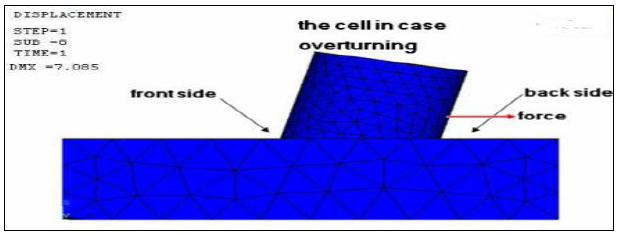
Wissmann [78] developed a PC application to examine mobile cofferdams using the finite detail method. The application uses quadrilateral axisymmetric ring detail to represent the soil and a cylindrical shell element to symbolize steel sheet piles. No slippage among piers is assumed it is measured as one body. There is an isolated circular mobile cofferdam cell with a diameter of 19.74 m and a peak of 7.55 with symmetric loading across the vertical axis case and another round cell with a diameter of 19.74 m and a height of 17.66 m with lateral load due to lower backfill cellular and tension force within the connecting region among the arch. Stresses for soil and metallic sheet piles are computed with a deflection for soil and sheet pile inside the exclusive level (Fig. 2).
The final depth of the excavation is 11 m with four levels of struts at depths of 1 m, 3.5 m, 6 m, and 4,5 m. The length of the sheet piles below the bottom of the excavation is 6 m, while the depth to the underlying hard stratum is 39 m. A constant undrained shear strength of 35 KN /m 2 is used in the analysis. To perform a finite element analysis, the geometry models created for the structure were driven into the soil with height to embedment depth ratios of 0.4H, 0.3H, and 0.2H for a cell width to height ratio of 1.00.
To establish the boundary condition, the standard fixities option was used. As a result, a full fixity at the base and free condition at the horizontal side of geometry was generated. The point loads are taken in state failure of cellular cofferdam in the laboratory tests.
Fabric residences are required for most element types. Depending on the software, fabric properties can be linear or nonlinear, isotropic, orthotropic or anisotropic, and consistent temperature or temperature based. The cloth library documents additionally make it feasible for numerous customers to proportion commonly used cloth facts.
3. RESULTS AND DISCUSSION
Sequentially coupled hydrodynamic-mechanical analyses are conducted in this study. Before describing the specifications of a structural model to investigate the behaviours of the cofferdam, the ocean environment, and the hydrodynamic model to calculate wave loads are explained.
An ocean environment is selected as a target site. The sea condition is applied based on site investigation KEPRI [79] where it is tested for offshore wind energy generation. The average water depth of the site is 10 m. According to DNV-OS-H101 [80], wave conditions should be determined based on a marine operation reference period. Because this period is expected to be about 3 months for a cofferdam, extreme sea state with a ten year return period is assumed; average current velocity, wave height, and wave period are 1.056 m/sec., 5.97 m, and 9.91 sec., respectively. To prevent wave overtopping, the air gap is assumed to be 6.28 m. The cofferdam is too large to be lifted by a general marine heavy lifting crane; although it is possible, high rent costs are expected. To solve this problem, cofferdam segments are used and assembled in a longitudinal direction. This approach requires a normal lifting crane to install each segment instead of large offshore cranes, decreasing construction costs. However, problems related to connection work between each segment and leakage at the connection interface exist. These difficulties can be overcome by special connection joint and rubber packing.
To calculate hydrodynamic pressures on the cofferdam, a numerical model for hydrodynamic analysis is created. Water waves with and without current are applied on the circular cylinder with a diameter of 20 m and a height of 16.28 m. The cofferdam cylinder is assumed to be fixed to the seabed.
The behaviour at the interface between segments is not included because the hydrodynamic model used is analysed by the panel method, which considers a structure body as a rigid body and a boundary condition. In the model, the interaction between water and connection flanges is ignored because flange thickness is small therefore the effects of the flanges are small. The vertical support columns are also not included in the model. Using the model, hydrodynamic pressure including current effects is calculated and provided as an external force in the structural model.
Experimental laboratory tests are conducted to analyze the response of the cofferdam. Cofferdam models with plane and corrugated cross-sections are simulated. All of the models are created using shell elements as shown in Fig. (3). The plane cross-section model had thicknesses of 10, 15, and 30 mm. The corrugated cross-section model had thicknesses of 9.65, 15, and 30mm. It also had a pitch of 500 mm, a depth of 237 mm, a tangent angle of 55.9 °, and a tangent length of 195.6 mm. In reality, the cofferdam consists of three segments and a suction bucket foundation.
However, in this study, the seabed is assumed to be strongly confined by the suction bucket and the cofferdam is considered to be fixed to the seabed.
External forces on the cofferdam are hydrostatic pressure and hydrodynamic pressure including the current. The hydrodynamic pressures with phase angles 0, 45, and 90˚are applied sequentially to the crest, middle, and trough of the wave, respectively. The bottom of the cofferdam is fixed to the seabed, and each segment is connected with a rigid joint. Each segment has a height of 5 m and the width of its flange is 5 mm (Fig. 3).
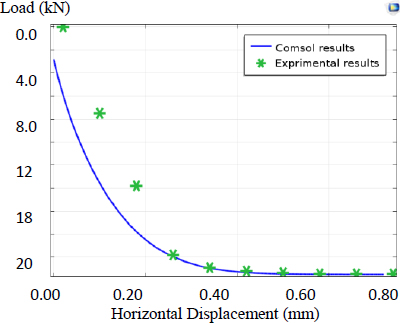
Before examining the stress distribution and deformation of the cofferdam, surge forces acting on the two cofferdams are compared. In the hydrodynamic diffraction analysis, the surge force for the plane cross-section is greater than that of the corrugated cofferdam; the latter’s surge force is 93% of the former’s. Changes in the resultant surge force over water depth are evaluated. Independently of the wave phase and cross-section type, the surge force increased as water depth increased weak-nonlinearly (Fig. 4).
The application of hydrodynamic pressures with the current, which are calculated from hydrodynamic diffraction analysis models, maximum stresses, and deformations of the two cofferdams with different thicknesses, was investigated. As indicated in Figs. (5 and 6), surge force is dominant in the two cofferdams; consequently, the cofferdam with the corrugated cross-section is largely deformed and had high stresses. Its maximum stresses and the maximum radial displacement were 637.72 MPa and 33.66 cm, respectively, when the water wave had a phase of 90°. By contrast, for the plane cross-section, the values were 164.02 MPa and 7.56 mm, respectively (Figs. 7 and 8).
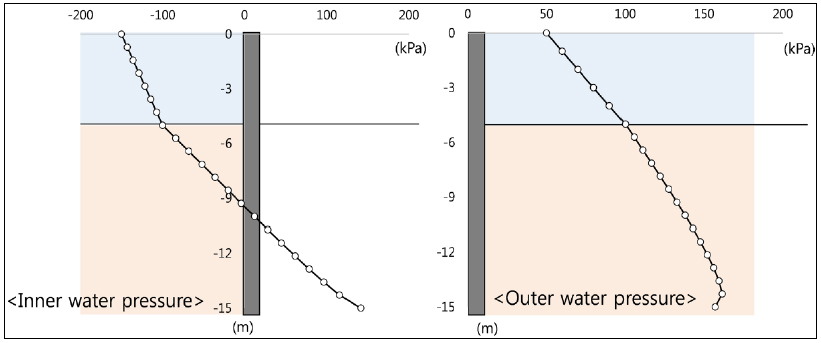
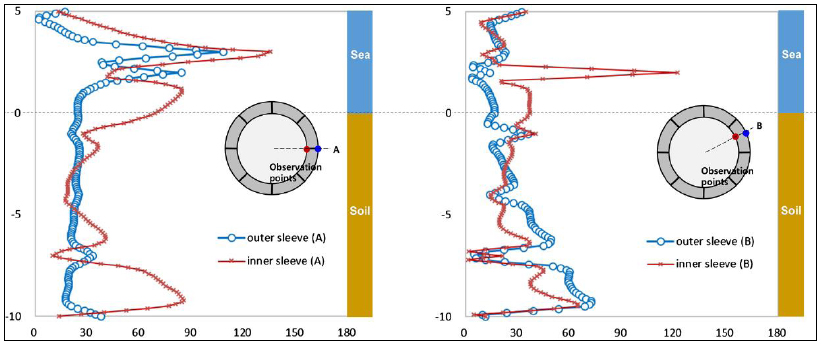
In Fig. (9), it is shown that by comparing the blue and red lines for the outer and inner sleeves near the vertical support, the bending and lateral force of the lid causes a sharp increase in stress. Also, the inner sleeve seems to be governed by the bending of the lid because smoother stress changes in the outer sleeve were observed overall. The inflection points of the stress profile curves occurred due to the circumferential stiffeners between the walls. The overall stress changes of the inner sleeve are relatively remarkable as compared to the outer sleeve. This would be caused by water pressure due to suction; if water pressure due to self-weight is a major factor, the stress profile along the height must be more proportional to vertical positions. Although the suction pressure increased from 100 kPa to 150 kPa, the pattern of stress profile was not changed; only the stress magnitude increased.
Thus, the magnitude of suction is the most important design factor of the bottom segment. Unexpectedly, the upper part of the outer sleeve had low stress irrespective of the contact condition. This means that the effects of wave pressure with the tidal current are small and could be ignored in the installation stage.
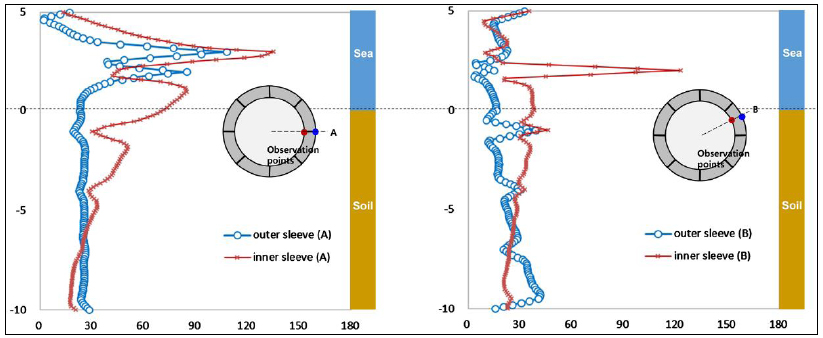
Stress profiles for model B with and without seepage pressure are shown in Figs. (10 and 11). Note that hydrostatic pressures on the sleeve walls disappear by offsetting as shown in Fig. (9). The contact condition applied to the interface was Case 1. It shows that the seepage water pressure causes a considerable difference between the stress profiles in Figs. (10 and 11) [81]. The maximum von Mises stresses of the models were similar to each other because of the contact effect between the lid and the segment wall. However, as seepage penetrated the bottom segment and increased water pressure, the stress profile patterns of the inner sleeve were significantly changed. The maximum stress increment of the inner sleeve is about 60 MPa near the bottom. Stress increases also occurred in the outer sleeve particularly for observation point B, where they became double near the bottom. The above results show that water pressure change due to seepage should be considered in the structural analysis of this type of cofferdams for the design of stiffener arrangement and plate thickness [81].
CONCLUSION
This study analysed the behaviours of cofferdams to examine the possibility of their application as an alternative to conventional cofferdams consisting of cellular retaining structures. To represent the realistic responses of cofferdams, this study conducted sequentially hydrodynamic structural analysis. The shear resistance to surge force at the interface is nearly independent of cross-section types, and changes in hydrodynamic pressures over cross-section types are about 7%. The resistance of cellular retaining structures with wet soil fill in saturated soils was greater than structures with dry soil fill in dry soils, and the increase of resistance for embedment depth ratio 0.4H was equal to 54% for circular cells and 34% for diaphragm cells. The increase of resistance for the berm ratio at 0.4H was equal to 59% for circular cells and 42% for diaphragm cells.
The cellular cofferdams in case hydrostatic pressure unable executed embedment depth, especially in rock foundations.
Through the above analyses, our results show that the stresses rapidly disappear along the different heights, direct changes in water pressure due to suction are a main design load factor of the cofferdam, and stress profile patterns are similar to models with suction pressures of 100 kPa and 150 kPa. If the bearing capacity of the seabed is small, the cofferdam behaviours can be governed by other external loading factors and water pressure change due to seepage is overall linear. Although nonlinear seepage effects appear near the skirt tip, this area is small and can be ignored. The application of water pressure due to seepage causes significant changes in stress profile patterns of the inner sleeve. Seepage effects should be considered for the basic design of the cofferdam and examination of contact effects is recommended as part of the design detail.
We recommend replacing the embedment depth by a berm in the event of embedment depth resistance or load failure. This would replace the trapezoidal berm ratio from 0.4H to 0.46H. The statistical models are created to find the relationship between horizontal displacement and width to height ratio (b/H), berm ratio, and embedment depth ratio after applied failure load. Thus, the use of a height ratio (b/H) of cofferdams for offshore bridge piers is not appropriate, and reinforcement measures are needed to support the cofferdam.
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
All data of this paper used to support the findings of this study from experimental work are available from the corresponding author [R.A.A.A.S] upon request.
FUNDING
None.
CONFLICTS OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
The authors would like to thank their colleagues from the department of civil engineering at the university of Babylon for their support during the experimental work.


