All published articles of this journal are available on ScienceDirect.
Dog-bone Samples may not Provide Direct Access to the Longitudinal Tensile Strength of Clear-wood
Abstract
Background:
Testing standards prescribe dog-bone samples for the determination of clear-wood longitudinal tensile strength. However, the literature reports a high number of invalid tests due to the unexpected failure of the sample outside the gauge length.
Motivation:
The paper aims at understanding the reason for the premature failure of dog-bone samples and suggesting possible strategies for improving testing protocols.
Methods:
The paper starts with a comparative review of standards for different orthotropic materials. Thereafter, it analyzes the stress distribution in a clear-wood dog-bone sample using a recently proposed stress-recovery procedure and Finite Elements. Finally, the sample failure is considered applying Tsai-Wu and SIA criteria.
Results:
Comparative review highlights the controversy on the choice of the sample geometry. Both analytical and numerical results confirm the presence of shear and transversal stresses in necking regions, overlapping with axial stress greater (up to 2%) than the one in the gauge region. As a consequence, clear-wood dog-bone samples fail not due to a pure axial stress state in the gauge region (as expected), but due to complex stress state in necking region, where failure index is 4 ~ 5% greater than the one in gauge region.
Conclusion:
Assuming that dog-bone samples fail in the gauge region due to pure axial stress is simplistic, as demonstrated by analytical and numerical evidence. As a consequence, interpretations of experimental results based on this belief are misleading and testing protocols should be refined. Indeed, the presence of spurious stresses interfering with expected pure axial stress seems unavoidable. Therefore, clear-wood testing standards should allow to use prismatic samples or, alternatively, to consider as valid also tests on samples breaking outside the gauge region. Both the proposed solutions apparently reduce the accuracy of the experiments, while in contrast, they provide the best achievable results, speeding up the testing procedure and reducing the testing costs.
1. INTRODUCTION
Experimental determination of mechanical properties of materials is fundamental in civil, mechanical, and aeronautical engineering. Indeed, research, industry, and engineering communities have developed standards defining testing procedures to be used for the determination of mechanical properties of different materials since the end of the Nineteenth century [1].
Nowadays, testing standards still represent a challenge. The periodical review of the existing standards and the definition of new ones allow us to get an idea of the complexity of the topic [2]. Indeed, the setting-up of an experimental procedure has to account for different -potentially conflicting- issues like sample geometry, clamping mechanism, material properties, representative volumes, imperfections, measur- ement systems [3]. In addition, the continuous technological improvements in both material processing and testing devices compel for continuous updates of systems and procedures, leading the debate on testing standards to remain far away from being closed. However, also well-established assumptions and procedures hide unresolved issues, as discussed in the following.
1.1. Dog-bone Sample Mechanics, Background Knowledge and Critical Issues
As illustrated in Fig. (1), a dog-bone sample can be divided into five regions: two anchoring regions of length la, two necking regions of length ln, and a central gauge region of length lg, usually equipped with some device for measuring strain. Well established knowledge e.g., (Section 1.3) [4], states that
(1) The gauge region is subject to a uniform distribution of pure axial stress, according to Saint-Venant solution [5],
(2) The anchoring regions and their neighborhoods are subject to transversal stresses and stress concentrations produced by the jaws of the testing machine,
(3) Necking regions connect the anchoring and gauge regions of the sample, allowing stresses to regularize and redistribute and avoid any interference of the anchoring system on the measurements performed in the gauge region.
Furthermore, the smooth reduction of the cross-section area in necking regions increases the magnitude of axial stresses. As an assumed consequence, the maximal stress -and consequently also the failure- should occur in the gauge region, under well-known and controlled stress state, providing reliable information on axial stiffness (not considered in this paper) and strength of the material. Consistently, testing standards specify that the test is valid only if a failure occurs in the gauge region.
The so-far discussed analysis of the mechanical behavior of dog-bone samples loaded with an axial force is a consolidated knowledge also in timber engineering. Indeed, the use of dog-bone samples for testing clear-wood mechanical properties along grain direction is well documented in both scientific literature [6] (Chapter 9) and standards. However, the premature failure of samples outside the gauge region is often reported in literature [7-9] and also confirmed by laboratory activity. More in detail, Eberhardsteiner (Section 3.2.2) [9] notices the failure of approximately 60% of the tested samples in the necking region.
Approaching the problem from a more general perspective, recent publications point out the non-trivial stress distribution in beams with variable cross-section. Paglietti and Carta [10] remark the fact that in tapered beams behaving in plane stress, shear stress distribution has no longer the well-known parabolic distribution with vanishing magnitude at cross-section boundaries, as in prismatic beams. Furthermore, the authors also mention the fact that maximal shear stress may occur everywhere in the cross-section, while in prismatic beam maximal shear occurs at the cross-section neutral axis. More recently, Balduzzi et al. [11] highlight that, due to variation of the beam thickness, shear stress depends not only on transversal internal force (as usual for prismatic beams) but also on bending moment and axial internal force. Mercuri et al. [12] have refined the analysis considering also the distribution of transversal stress, while Patni et al. [13] extended the analysis to more general geometries. Finally, Bertolini et al. [14], Bertolini and Taglialegne [15] provide an accurate analytical stress-recovery for thin walled beams, confirming that any variation of the cross-section geometry leads to substantial modification of the stress state within the beam.
In addition to the problem of the non-trivial distribution of stress, also the highly anisotropic strength of the material has to be considered. Specifically, both shear strength and strength perpendicular to the grain are significantly smaller than the strength parallel to the grain for wood. Therefore, the existence of complex stress states (involving components parallel and perpendicular to the grain, and shear) near the boundaries where grain is not aligned with lateral surface can be extremely dangerous, dominating the failure mechanism. Consistently, timber design standards [16, 17] provide specific rules for tapered beams, requiring more accurate stress analysis and the adoption of enhanced failure criteria.
1.2. Paper Motivation, Hypothesis, and Outcomes
This paper aims at shedding light on the reasons for the premature failure of dog-bone samples and suggesting possible improvements for clear-wood testing standards. Consistently, the analysis will be limited to a homogeneous body, behaving under the assumption of plane stress and small displacements. The material is assumed to be linear-elastic and to exhibit a brittle failure. Furthermore, we assume that the sample is not affected by any geometrical, material, or manufacturing imperfections like deviations of grain direction, cracks or micro-cracks (both in the body and on the surface of the sample), manufacturing tolerances, stresses induced by jaws eccentricity, etc. Finally, we also assume that the experimental set-up (e.g., jaws geometry and pinching force, interference of measurement devices) has been properly designed, avoiding any influence on the test process and outcome.
The analysis presented in this document is based on (i) a comparative review of standards developed for different materials, (ii) analytical and numerical analysis of the stress distribution in samples, and (iii) a discussion of possible failure modes, based on two criteria, which use is well-established in the literature. The main outcome of the paper is the demonstration that the analysis of the mechanical behavior of dog-bone samples summarized in Section 1.1 is simplistic. Indeed, a non-trivial distribution of axial, shear, and transversal stresses in necking region causes the premature failure of the sample, leading, on the one hand, to the high invalid test rate documented in the literature and, on the other hand, to a misleading interpretation of experimental results.
The paper outline is as follows. Section 2 describes materials and methods: Subsection 2.1 comparatively reviews standards developed for different material, Subsection 2.2 develops a simplified analysis of stress distribution, based on the stress-recovery procedure recently proposed by Mercuri et al. [12], Subsection 2.3 describes highly refined 2D Finite Element (FE) analysis, and Subsection 2.4 introduces different criteria for the prediction of the sample failure. Section 3 describes obtained results: Subsection 3.1 highlights diffe-rences between standards developed for different materials and discusses additional information available in the literature, Subsection 3.2 discusses results of the simplified analysis of stress distribution, revealing the presence of spurious stresses in necking region, Subsection 3.3 presents numerical results obtained using highly refined 2D FE analysis, confirming the presence of spurious stresses, and Subsection 3.4 discusses the sample failure, showing that, according to different criteria, it occurs outside the gauge region and is driven by complex stress states. Finally, Section 4 provides final remarks and a brief discussion of future work development.
2. MATERIALS AND METHODS
2.1. Comparative Review of Standards and Literature
This subsection introduces prescriptions concerning the geometry of the sample to be used for the determination of tensile strength of wood, unidirectional fiber reinforced plastic, polymer matrix composites, and fiber reinforced plastic. All the previously cited materials are highly orthotropic and have a reduced strength in directions perpendicular to the fibers.
In wood engineering and industry, standards [18-20] prescribe a dog-bone sample for testing clear-wood along the grain direction. Specifically, standard DIN 52 188-79 [18] prescribes single tapering i.e., the smooth, symmetric reduction of the sample thickness only, while others [19, 20] prescribe double tapering i.e., the smooth reduction of both thickness and depth. Conversely, in the field of artificial composites, standards [21, 22] prescribe a prismatic geometry for fiber reinforced plastic and polymer matrix composites, respectively. In detail, standard ISO 527-5 [21] prescribes the use of end tabs, to be inserted between the jaws and the sample, while standard ASTM D 3039M [22] specifies that they are not mandatory. Finally, three types of test samples are considered in standard ISO 527-4: Dog-bone, prismatic without end-tabs, and prismatic with end-tabs for fiber-reinforced plastic composites [23]. Table 1 resumes the prescriptions provided by different standards.
2.2. Analytical Recovery of Stress Distribution
The stress-recovery discussed in this subsection is the specialization of the procedure proposed by Mercuri et al. [12] for non-prismatic beams to the case of a symmetric beam under uniform axial load. Consistently, the analysis is limited to necking and gauge regions, while the proposed analytical stress-recovery cannot provide any information on the distribution of stresses in anchoring regions and in their neighborhood. The stress-recovery procedure exploits 2D equilibrium Partial Differential Equations (PDEs) and standard assumptions on the distribution of axial stresses in slender bodies.
Neglecting the weight of the material, the 2D equilibrium PDEs read
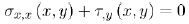 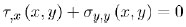
|
(1) |
Since upper hu (x) = h(x)/2 and lower hl (x) = −h(x)/2 lateral surfaces (Fig. 1) are unloaded, boundary equilibrium reads

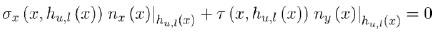 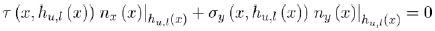
|
(2) |
where the outward unit vector is defined as:
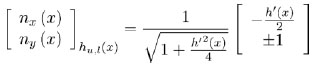 |
(3) |
We assume that the axial stress has a uniform distribution within the cross-section also in necking region, in analogy with the prismatic beams subjected to a pure axial load
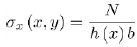 |
(4) |
Substituting Equations (3) and (4) into Equation (2) allows expressing the boundary equilibrium as
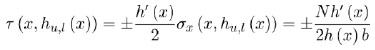 |
(5a) |
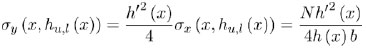 |
(5b) |
Meaning that shear and transversal stresses do not vanish on the boundaries of the necking region, but are proportional to the axial stress and the slope of the lateral surface. As a consequence, boundary equilibrium is enough to demonstrate the presence of shear and transversal stresses in the necking region. This peculiarity of beams with variable thickness is well known in literature [24-26] and considered also in design standards [17, 16] where, however, specific prescriptions are provided for bending only.
Using the horizontal equilibrium PDE (1a), the distribution of shear stress can be recovered:
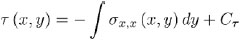 |
(6) |
where the constant of integration Cτ is determined in order to satisfy the horizontal boundary equilibrium (5a). In practice, Equation (6) means that any variation of the axial stress (including magnitude variation due to the reduction of the sample cross-section) is associated with some non-vanishing shear stress. Substituting Equation (4) into (6) and performing few elementary calculations lead the shear distribution to read
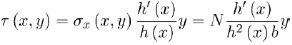 |
(7) |
Equation (7) highlights that shear stress has a linear odd distribution within the cross-section and it depends on the slope of the lateral surface.
Using the vertical equilibrium PDE (1b), the distribution of transversal stress can be recovered
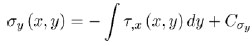 |
(8) |
where the constant of integration Cσy is determined in order to satisfy the vertical boundary equilibrium (2b). Substituting Equation (7) into (8) and performing few elementary calculations lead to the distribution of transversal stress to read
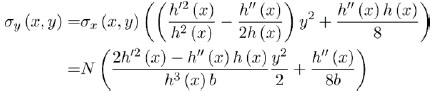 |
(9) |
Equation (9) highlights that transversal stress has a quadratic even distribution within the cross-section and it depends on both the slope and the curvature of the lateral surface.
Remark 2.2.1. As highlighted by Balduzzi et al. [11], the proposed stress-recovery is not able to handle boundary effects. As a consequence, it is expected to be unable to predict stress concentrations near the anchoring region and in the neighborhood of any sudden change of the body geometry.
Remark 2.2.2. Using stress-recovery (4), (7), and (9) in the gauge region, stress distribution reduces to σx (x, y) = N/hmb and τ (x, y) = σy (x, y) = 0, confirming the capability of the proposed approach to recover analytical solutions available in the literature.
Remark 2.2.3. The distribution of axial and transversal stresses is even with respect to the x axis according to Equations (4) and (9), while the distribution of shear is odd according to Equation (7), also leading to vanishing, resulting in transversal force.
At x = 0 i.e., at the conjunction between necking and gauge regions, the geometrical properties of the cross section read
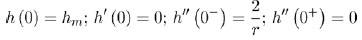 |
(10) |

Where 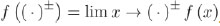 . Consistently, Equations (4), (7), and (9) read:
. Consistently, Equations (4), (7), and (9) read:
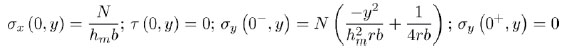 |
(11) |
The analytical stress-recovery points out that transversal stress does not vanish as x = 0 mm, despite the smooth connection between necking and gauge regions. In particular, a discontinuity in the distribution of transversal stresses occurs due to the discontinuity of the lateral surface curvature. Such a phenomenon does not have a physical meaning, but is uniquely a consequence of simplified model hypothesis (Remark 2.2.1).
2.3. FE Analysis
We consider the planar domain depicted in Fig. (2) i.e., the clear-wood dog-bone sample as defined in standard DIN 52 188-79 [18], considered in the following numerical example. The sample has been loaded with a unit force H = 1N. The choice of the testing standard is arbitrary. Indeed, conclusions can be easily generalized to all dog-bone samples, independently from the specific sample measures.
Due to the symmetry of geometry and loads, we analyzed only the left upper quart of the sample, constraining displacements perpendicular to the symmetry planes. Using the commercial software Abaqus [27], the domain has been discretized with a structured mesh of 940000 CPS3 triangular elements (4701 × 101 uniformly distributed nodes). The choice of the mesh guarantees a negligible numerical error in the computed solution.
Load has been applied imposing a unit uniform horizontal displacement to nodes on the lateral surface of the anchoring region, leading to a constraint equivalent to the one depicted in Fig. (2). Stresses have been later normalized in order to produce a resulting axial force of H = 1N. The mechanical configuration introduced so far leads to some spurious stress concentration in the anchoring region. However, stress concentrations occur sufficiently far away from the portion of the sample we are analyzing. Consequently, we decided to avoid any model refinement in the anchoring region, since the obtained numerical results are enough for the analysis we are performing.
The material has been assumed to be linear elastic and orthotropic, adopting mean values of mechanical properties of Norway spruce as specified in standard ÖNORM B 3012 [28] (E0 = 12500 N/mm2, E90 = 450 N/mm2, G = 650N/mm2, and ν0−0-90 = 0.015). The mechanical properties of clear-wood has been chosen in order to assign typical values to the parameters that have to be introduced in the FE software input and not for simulating the testing of a specific material, according to the general purpose of the present paper.
2.4. Definition of Failure Indexes
Failure Indexes (FIs) are used for the definition of the failure surface for anisotropic materials, requiring FI = 1. Supposing a brittle behavior of the material, the location of the maximal value of FI represents the point where the failure of the sample begin, instantaneously propagating to the whole sample cross-section. Specifically, we consider two possible FIs for clear-wood: (i) the Tsai-Wu FI [29] and (ii) the FI defined according to SIA 265 [30], the use of which is well established in timber engineering.
The Tsai-Wu FI [29] is defined as:
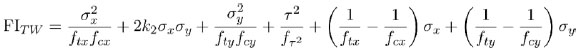 |
(12) |
Tsai-Wu FI (12) accounts for the interaction of all stress components, it can be placed in a more general and mathematically rigorous context [31], and it has also been validated against experimental results [32].
The FI defined in SIA 265 [30] is as follows:
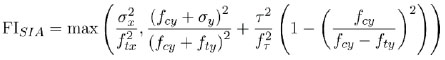 |
(13) |
On one hand, the Schweizerischer Ingeneur und Architek- tenverein (SIA) FI (13) does not consider the interaction between axial stress and the other stress components, resulting, therefore, in less rigorousness than Tsai-Wu FI (12). On the other hand, the expression accounting for the interaction between shear and transversal stresses is based on an extensive experimental campaign [33].
As characteristic strengths, the parameters for the Norway spruce, as specified in standard ÖNORM B 3012 [28], has been assumed, leading to set
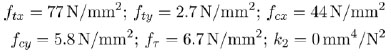 |
(14) |
As already specified in Section 2.3, the mechanical properties of clear-wood have been chosen in order to assign typical values to the parameters that have to be introduced in FI and not for simulating the testing of a specific material.
3. RESULTS AND DISCUSSION
3.1. Comparative Review of Standards and Literature
Table 1 clearly shows that the geometries of wood, unidirectional fiber reinforced plastic, polymer matrix compo- sites, and fiber reinforced plastic samples are substantially different, despite (i) a similar mechanical behavior of the material and (ii) all the testing standards aim at determining the same mechanical property. In other words, different engineering communities approach similar problems in completely different manners, maybe due to differences in the background education and the historical evolution of the various engineering branches.
Consistently with well-established knowledge [4, 18-21], specify that the test is valid only if the failure occurs in the gauge region. Conversely, other standards [21-23] do not provide any indication and/or constraint to the location of the failure in prismatic samples. Only standard ASTM D 3039M [22] recommends the set-up of a test configuration that could lead the failure to occur in the central part of the sample. As a consequence, artificial composites testing standards seem to underestimate issues related to stress concentration, ultimately leading to an apparently less rigorous interpretation of the testing results.
Indeed, Wisnom and Maheri [34] proposed to use dog-bone samples for the determination of tensile strength of carbon epoxy composites. The reason of this choice is that prismatic samples lead the failure to initiate in the tab region due to stress concentration and the estimation of the material strength to be ≈ 15% lower than the one obtained using tapered samples. However, experimental results highlight that the failure of dog-bone samples initiates with a delamination in the necking region, suggesting the presence of some transversal or shear stress. Any detailed analysis of the phenomena has been discussed and the proposed geometry, having constant tapering ratio in necking region, displays sudden changes in the geometry that are expected to exacerbate the problem of stress concentration.
In the field of timber engineering, the premature failure of the samples has often been justified by the presence of defects on the sample surface. As an example, Kohan et al. [7] compare the modulus of elasticity and the ultimate tensile strength of wood strands obtained using prismatic and dog-bone geometries. In their paper, the authors states that the “Samples damaged during cutting of bone geometry were discarded. This happened more frequently than expected as a result of unseen micro-defects from the stranding process. This resulted in a smaller sample size for the dog-bone-shaped specimens (n=24) than for the rectangle-shaped specimens (n=67)”. More recently, Karwat and Koczan [8] propose the use of cylindrical samples instead of rectangular ones for testing clear-wood. “The motivation behind this decision came from the fact that a sample with circular section minimizes the lateral area at a determined cross-section and height of a sample. A small lateral area reduces the probability of surface defects. Also, a cylindrical sample does not have any sharp edges prone to be damaged”, [8].
The problem of failure in necking regions has also been approached using numerical techniques. Gašparík et al. [35] evaluate the distribution of stresses within a wood dog-bone sample using 3D FE analysis. However, the authors used an isotropic-like material during simulation (only a Young’s modulus and a Poisson’s coefficient for every material have been defined) and simplified failure criteria (only tensile and shear strengths parallel to grain have been considered), maybe leading to a too coarse approximation of the problem and impeding an effective analysis.
Morais et al. [36] proposed a more accurate analysis, performing a detailed 3D FE analysis of different sample geometries. The obtained results “clearly indicate that failure is due to stress concentration effects and occurs under a complex stress state”. Experimental results reported in the paper confirm numerical evidence. Indeed, sample failure typically initiates at the conjunction between necking and gauge regions, and not in gauge region as expected. However, the authors considered a sample with a small radius in necking regions (r = 16 mm), associated with a rapid variation of sample geometry, more prone to stress concentration. Conversely, standard DIN 52 188-79 [18] prescribes a larger radius (r = 713 mm), leading to a smoother geometry that is expected to mitigate stress concentration effects.
Büyüksari [37], Büyüksarı et al. [38, 39] analyze micro-sized samples, considering different wood species and the influence of several parameters. However, the geometry of micro-sized samples has been defined just scaling standard size samples, using dog-bone shape. Finally, the connection between anchoring region and region or volumes subjected to mechanical investigation by means of necking elements has been generalized also to bi-axial test samples [9].
On the side of composite testing, standard ISO 527-4. [23] specifies that dog-bone samples “may be used for fibre-reinforced thermosets if they break within the gauge length”. Such a clause suggests that a failure outside the gauge region is somehow expected for dog-bone samples. To crown it all, the problem of the failure outside the gauge region is also documented in literature. Ahn et al. [40] provide documentary evidence of the failure in the necking region for dog-bone samples obtained using a Fused Deposition Modeling (FDM) process and Acrylonitrile Butadiene Styrene (ABS) plastic. More recently, Alaimo et al. [41] “observed that dog-bone samples fail prematurely at the stress concentrations or at the bi-axial stress state zones, i.e. at radius level, while the rest of the specimen remains intact” during testing of FDM ABS plastic samples. The problem of failure of dog-bone shaped FDM samples at the conjunction between necking and gauge regions has also been reported [42, 43]. However, both papers refer to standard ASTM D638-14 [44] and other standards originally developed for plastic injection parts. Also, Ferreira et al. [45] referred to standard ASTM D638-14 [44] and used dog-bone samples for the determination of tensile stiffness and strength of FDM Poly-Lactic Acid (PLA) and PLA reinforced with short carbon fibers, but any information concerning the failure mode is reported in the paper. To the best of the author’s knowledge, any detailed analysis of the stress state in FDM samples has been carried out.
A comparative review of testing standards highlights that the choice between dog-bone and prismatic sample is not trivial. Furthermore, literature reports the frequent failure of dog-bone samples outside the gauge region, independently from the material. Finally, few numerical investigations highlight the existence of additional stress components in the necking region that may negatively influence the experimental outcome.
3.2. Analytical Recovery of Stress Distribution
Fig. ( 3 ) reports stress distribution in the region −60 ≤ x ≤ 20 and y ≥ 0, since it is the portion of the sample where investigated phenomena occur. The solution for y < 0 can be easily recovered exploiting symmetry of the solution, as specified in Remark 2.2.3. According to Remark 2.2.2, the distribution of stress is a pure and uniform axial tension in the gauge region of the sample. Conversely, some transversal and shear stresses occur in the necking region, despite, they are not considered in both standard beam theories and background knowledge of testing standards [4]. Specifically, shear and transversal stresses are approximately one and two orders of magnitude smaller than axial stress, respectively. As already highlighted discussing Equation (11), the distribution of transversal stress presents a discontinuity i.e., an inconsistency between necking and gauge regions of the sample, due to the simplified hypothesis behind the beam model (Remark 2.2.1). In reality, some local effects including cross-section warping and non-linear distribution of axial stresses- are expected at the conjunction between necking and gauge regions [46].
Concluding, analytical stress recovery indicates the presence of both transversal and shear stresses in the neighborhood of x = 0, where axial stress already reached its maximum. As a consequence, the failure of the sample will always occur outside the gauge region or on its boundary, invalidating the test. Furthermore, as already highlighted by Morais et al. [36], the failure is the consequence of the interaction of axial, shear and transversal stresses, impeding the straightforward interpretation of the experimental results indicated in testing standards.
3.3. FE Numerical Results
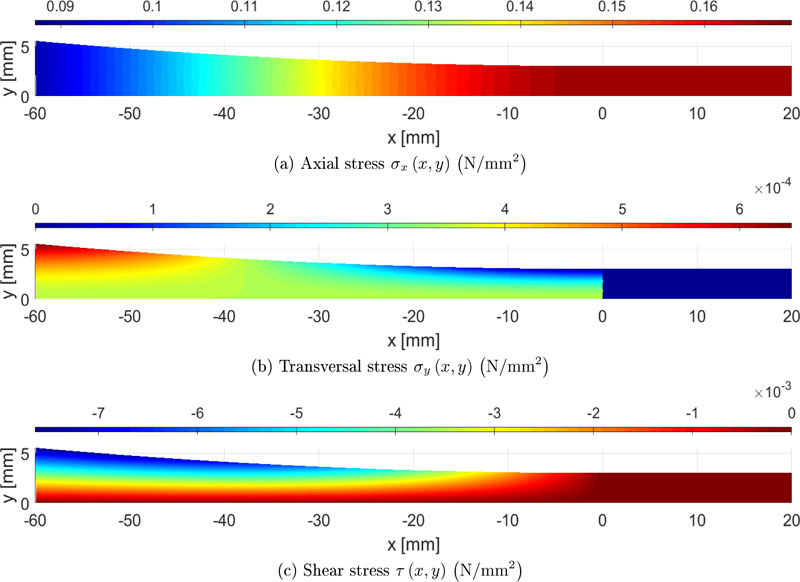
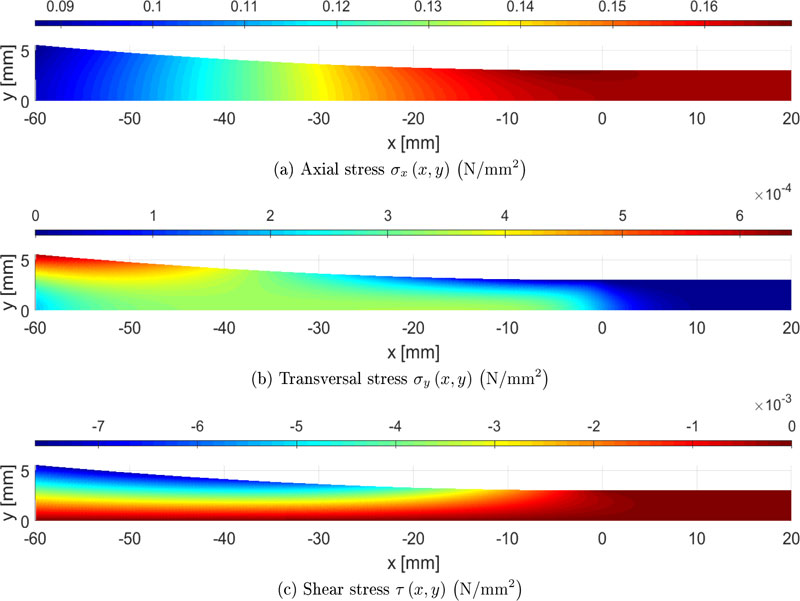
This section discusses some FE results, aiming at validating the analytical stress-recovery introduced in Section 2.2 and confirming evidence about the presence of additional stress components in necking regions.
Fig. ( 4 ) reports stress distribution coming from FE analysis in the region −60 ≤ x ≤ 20 mm and y > 0 only. Numerical results are in good agreement with the analytical results depicted in Fig. (3). The only noticeable differences are (i) a non-uniform distribution of the axial stress in the cross-section (Figs. 3a and 4a), (ii) a smooth distribution of transversal stresses in the neighborhood of x = 0 mm (Figs. 3b and 4b), and (iii) the propagation of transversal and shear stresses in the gauge region (Figs. 4b and 4c). The non-uniform distribution of axial stress is an expected consequence of the different hypotheses used in the two analysis approaches. Indeed, the analytical stress-recovery assumes that the cross-section behaves as a rigid body while such a hypothesis has not been implemented in the FE analysis. The smooth distribution of transversal stresses and the propagation of transversal and shear stress in the gauge region is a consequence of the capability of FEs to model boundary effects, differently from simplified analytical stress-recovery (Remark 2.2.1).
In addition to the presence of both transversal and shear stresses, the FEs also highlights that, at (x, y) = (−2.50,3.00) mm, axial stress magnitude (≈ 0.170 N/mm2) overcomes the magnitude of axial stress in gauge region (≈ 0.167 N/mm2), with a difference of approximately 2%. As a consequence, the theoretical failure is expected outside the gauge region, due to a non-uniform distribution of axial stress, combined with other stress components.
Differently from analytical results discussed in Section 2.2, FE results depend on material stiffness. Indeed, different ratios between Young’s moduli in axial and transversal direction modify the length of the area in which boundary effects are significant within the gauge region. Such a result well known and documented in the literature [47, 48] highlights a further critical issue that has to be considered in testing anisotropic materials: The length needed for the extinction of boundary effects.
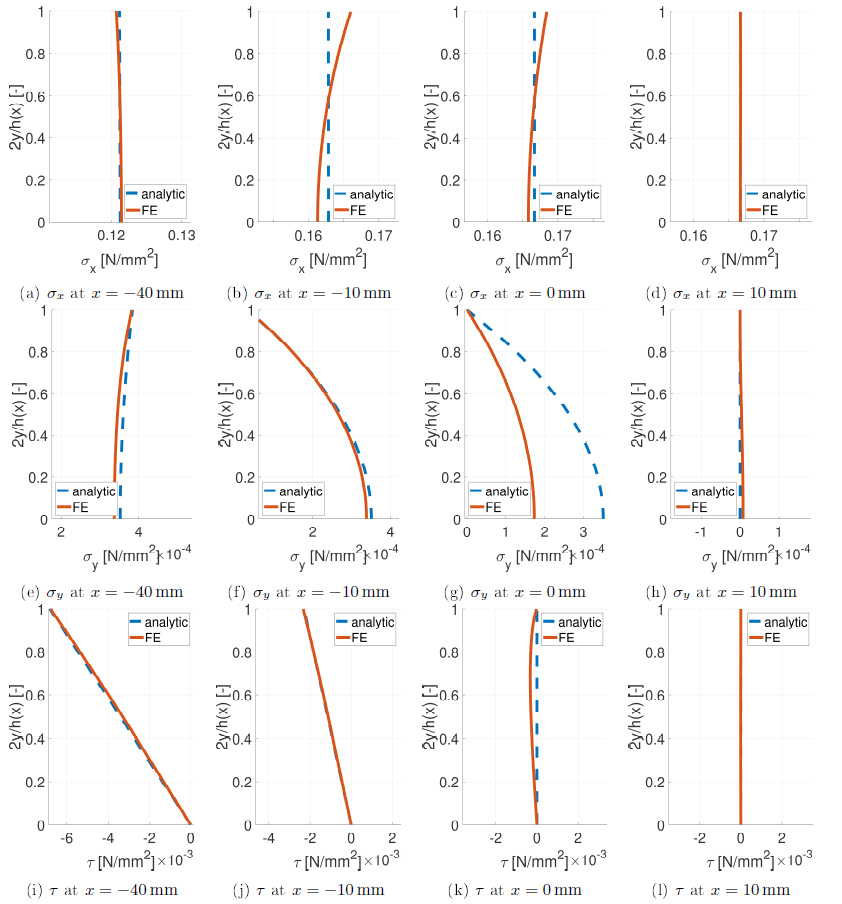
For a more rigorous comparison of the results, Fig. (5) depicts the distribution of stress components in sample cross-section at x = −40,−10,0, and 10 mm, obtained according to analytical stress-recovery and the FEs. The cross-section distribution of stress confirms the good agreement between analytical and FE results. The only substantial differences are at x = 0 mm, as already extensively discussed in this section. In correspondence with the analytical results inconsistency, some local deformation of the cross-section occurs, leading to a non-uniform distribution of axial stresses (Fig. 5c) and smearing the distribution of transversal stresses in the neighborhood of the considered cross-section (Fig. 4b) [46-48].
Concluding, also FE results confirm the statement at the end of Section 2.2: Stress distribution induced by necking of the sample should lead to the premature failure of the sample outside the gauge region, invalidating the test. Such an analysis is consistent with (i) information provided in literature [21, 36], (ii) experimental results [36, 40], and (iii) high number of invalid test documented in the literature [7-9]. Finally, the problem highlighted in this section is expected to be exacerbated considering the double taper and smallest radius of the necking zone, as recommended in standard ASTM D143-94 [19].


3.4. Location and Magnitude of FI
Fig. ( 6 ) depicts the distribution of Tsai-Wu FI, obtained by scaling the results of FE analysis in order to obtain FITW = 1 in the gauge region. Tsai-Wu FI reaches the maximal magnitude at (x, y) = (−3.50, 3.01), outside the gauge region. Furthermore, the ratio between maximal FI and FI in the gauge region is ≈ 1.05, indicating that the interaction of axial stress with both shear and transversal stresses leads to the failure of the sample to occur earlier and farther away from the location of maximal axial stress (x, y) = (−2.50,3.00) mm. Finally, such a high ratio is consistent with indications provided [23, 36], confirming that the failure outside the gauge region has to be expected, invalidating most of the tests.
Fig. ( 7) depicts the distribution of SIA FI, obtained scaling the results of FE analysis in order to obtain FISIA = 1 in the gauge region. max(FISIA) = 1.04 and it is located at (x, y) = (−2.50, 3.00) mm i.e., at the same location of maximal axial stress. As a consequence, it can be easily concluded that, according to SIA criteria, the failure occurs outside the gauge region, despite it is driven by axial stress only.
CONCLUSION
This paper analyzed the distribution of stress within clear-wood dog-bone specimen using an analytical stress-recovery and a refined 2D FE analysis. Both the methods agree indicating the presence of non-negligible transversal and shear stresses in the transition zone between necking and gauge regions. Furthermore, FEs also indicate that in the transition zone axial stress reaches magnitudes that are ≈ 2% greater than the one in the gauge region. Both Tsai-Wu and SIA failure criteria indicate that, in the necking region, the FIs reach magnitudes that are 4 ~ 5% greater than the one in the gauge region, confirming the complexity of the failure mechanism of the specimen. Such an analysis is consistent with experimental results reported in the literature. As a consequence, well-established beliefs that dog-bone samples fail in the gauge region due to pure axial stress turn out to be coarse and simplistic. Indeed, failure in the necking region i.e., an invalid test is the expected outcome and apparently valid results should be influenced by some other phenomena (imperfections, fiber deviation) not considered in the present study. Finally, the proposed refined analysis of stress distribution seems to indicate that the presence of spurious stresses interfering with a failure induced by pure axial stress cannot be avoided but just mitigated.
In light of the analytical and numerical evidences summarized above, the authors suggest the modification of the testing protocol nowadays used for the determination of ultimate tensile strength of clear-wood along the grain direction. The former solution is the use of prismatic specimens, with a proper design of anchoring system. The latter solution is to accept as valid also results of tests on specimens breaking outside the gauge region. In both cases, experimental results will be affected by spurious stresses, apparently reducing the accuracy of the testing procedure. Conversely, they are expected to provide the best achievable results. Furthermore, the testing procedure will become faster and cheaper, avoiding numerous invalid tests and reducing the manufacturing cost of the samples.
In future work, we will verify the effectiveness of the two proposed procedures (considering different geometries, anchoring system designs, measurement techniques) by means of suitable experimental campaign. At the same time, we will apply enhanced uncertainty quantification techniques, namely stochastic collocation and Galerkin methods, e.g., [49, 50] and perturbation methods [51], for modeling the randomness of grain direction and sample geometry imperfections. The comparison of both experimental and numerical results will allow defining the most convenient testing approach.
LIST OF ABBREVIATIONS
| FE | = Finite Element |
| PDE | = Partial Differential Equation |
| FDM | = Fused Deposition Modeling |
| ABS | = Acrylonitrile Butadiene Styrene |
| FI | = Failure Index |
| SIA | = Schweizerischer Ingeneur- und Architektenverein |
| PLA | = Poly-Lactic Acid |
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
The data supporting the findings of this article are available within the document.
FUNDING
None.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGMENTS
None.


