All published articles of this journal are available on ScienceDirect.
Seismic Ductility Reduction of Flexural-type Structures with Vertical Irregularities
Abstract
Seismic ductility reduction factors for flexural-type structures with vertical irregularities subjected to pulse-like and non-pulse-like ground motions are investigated in this paper. By establishing various multi-node flexural cantilever-column models, the ductility reduction factor of vertically irregular structures is studied by modifying the ductility reduction factor of irregular structures. The effects of various factors such as ductility level, irregular ratio and pulse-like earthquake excitation on modification coefficient are also explored. The analysis results reveal that: 1) the modification coefficient decreases with smaller irregularity ratio; 2) ductility reduction factors for vertically irregular structures are significantly smaller than those of regular structures; 3) ductility level exerts a certain influence on ductility reduction factor without an obvious trend; and 4) the modification coefficient under pulse-like excitation is smaller than those from non-pulse-like motions and the influence of pulse-like earthquake is coupled with irregularity ratio. This paper concludes with the statistical outcomes based on average of results and recommends modified factors for practice uses.
1. INTRODUCTION
Determining the value of Strength Reduction Factor (SRF) has always been one of the most controversial issues in the research of earthquake engineering around the world. SRF has different notations among researchers from different countries. For example, it’s referred as response modification factor (R) in International Building Code [1], force modification factor (R) in National Building Code of Canada [2], behavior factor in Eurocode (EC8) [3] and structural influence factor (C) (C=1/R) in Chinese building seismic design code [4]. Despite the difference in notation and value, SRF is universally recognized to consist of two major components: ductility reduction factor and overstrength reduction factor. In terms of the research on ductility reduction factor, it’s mainly decided by the ductility, material and type of a structure. EC8 [3] considers the effect of irregularity of the building in the vertical direction on the ductility reduction factor. It states that the ductility reduction factor for structures with irregularity in the vertical direction needs to be multiplied by a coefficient of 0.8.
Vertical irregularity in a structure is introduced by abrupt changes or discontinuities in the configuration (such as dimension, floor mass, stiffness, strength or their combination) along its vertical direction. As a consequence, large stress or plastic deformation concentration may occur in local weakness and propagate into global damage or even collapse. There is a large amount of literatures on this issue [5-10]. Soni [9] and Zhou [10] have a detailed literature review for the past three decades on the research of seismic buildings with vertical irregularities. The research can be summarized into three aspects: 1) the evaluation of the effectiveness on the parameters to limit building vertical irregularities in seismic design code; 2) analysis to characterize the seismic response of weak story; 3) developing effective measure in research and seismic design for buildings with vertical irregularity. With the fast development on high-rise buildings, the configurations for structures have become more and more complex. The analysis and evaluation on seismic performance of buildings with vertical irregularity have thus received more and more attentions from various researchers. However, the effect of pulse-like earthquake excitation on buildings with vertical irregularity is rarely investigated. In the 1970s, some researchers clearly addressed the need to consider the effect of pulse-like earthquake in the seismic design of the building [11]. A vast majority of researches within the past 30 years demonstrate that the demand on story drift and strength increase significantly under earthquake excitation with velocity pulse [9-12].
As a summary, although plenty of researches have studied either the seismic performance of vertically irregular buildings or the effect of pulse-like ground motion, few have focused on the situation when these two adverse conditions are combined together. In addition, previous research on ductility reduction factor has mainly focused on frames or MDOF systems that mainly undergo shear-type deformation [13-15], whereas there is no adequate research on shear wall structure which mainly develops flexural-type deformation. With the social and economic development, high-rise shear wall structures that mainly develop flexural-type deformation are more commonly employed in modern construction. The lateral deformation patterns of flexural-type structure and shear-type structure are distinct from each other and their story shear distributions are thus also different. It’s very necessary to have an in-depth investigation on the ductility reduction factor for shear wall structures which mainly have flexural-type behavior. Therefore, based on the previous research [15] on the ductility reduction factor for vertically irregular buildings subjected to ground motions with velocity impulse, this paper employs multi-node cantilever column to simulate the behavior of flexural-type structural systems and consider the unfavorable conditions of both vertical irregularity and velocity-impulse excitation to investigate the effect of irregularities, ductility factor, number of stories (vibration period) and velocity impulse components on the ductility reduction factor for buildings with irregularities in the vertical direction.
2. METHODOLOGIES
2.1. Input Ground Motion
The Pulse Index (PI) based on the velocity and energy [16] is used to indicate the intensity of velocity impulse in ground motion. PI has a range between 0 and 1, with 0.85≤PI≤1 as strong velocity impulse and 0≤PI≤0.15 as non-velocity impulse [16]. Ground motions in Table1 are used to represent the maximum effect of velocity impulse as the PI for each of them is 1.0. These 5 ground motions, with PGA to indicate their intensity, are selected and scaled such that the structure will reach the predefined ductility demand. Ground motions with non-velocity pulse-like are generated by filtering out the velocity impulse component from wavelet analysis [16, 18-19]. The continuous wavelet transform of the velocity time history is computed, and the coefficient with the largest absolute value is identified. The wavelet associated with this coefficient identifies the period and location of the pulse, as illustrated in Fig. (1b). This wavelet is subtracted from the ground motion, and the continuous wavelet transform is computed for the residual ground motion. An extracted pulse using ten coefficients is illustrated in Fig. (1c), and the residual ground motion after the pulse has been removed as shown in Fig. (1d). These ground motions are selected from the publication of Baker research group [17]. As the real earthquake is a random variable itself, the 5 pulse-like ground motions in Table 1 are randomly selected from the ninety-one pulse-like motions classified by Baker [16], to highlight this randomness and uncertainty. They are selected to cover different earthquake events.
2.2. Structural Model
In this paper, a multi-node cantilever column (Timoshenko-beam model) is used to simulate a shear wall structure that deforms mainly as a quadratic parabola under a reverse triangular distributed load. A structure can be reduced to a layered model by concentrating the total mass of each story on the top of the story. The whole structure is then simplified to a cantilever member. The following assumptions are made for this model: 1) The floor has infinite in-plane stiffness and all the vertical structural members of each story have the same lateral displacement under horizontal seismic load; 2) The center of stiffness of the system coincides with its center of mass so that no torsion is considered. According to the lateral displacement shape, the layered model can be classified into three types: shear-type, shear-flexural-type and flexural-type. The lateral deformation of the three groups is principally governed by bending, a combination of bending and shear, and shear, respectively. The inter-layer shear force and drift can be obtained from the layered model where the stress and deformation of each element are unable to be achieved. In practice, layered models are usually applied to examine the location of weak floors and check whether the story shear forces and story drift are beyond the permitted maximum value, respectively.
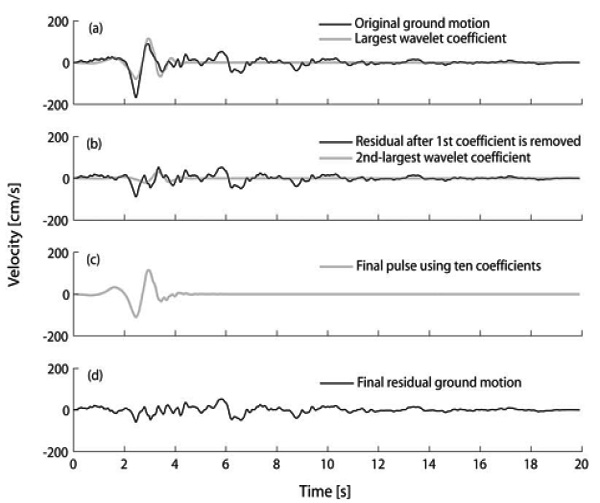
Illustration of the decomposition procedure used to extract the pulse portion of a ground motion (the fault-normal component of the 1994 Northridge recording).
List of pulse-like ground motions used in the present study.
| Event and year | Record Station | Moment Magnitude | PGA/ (cm/s2) | PGV/(cm/s) | PI |
|---|---|---|---|---|---|
| Imperial Valley, 1979 | EC Meloland Overpass FF | 6.5 | 263.32 | 115.0 | 1.00 |
| Superstition Hills, 1987 | Parachute Test Site | 6.5 | 388.87 | 106.8 | 1.00 |
| Loma Prieta, 1989 | Oakland - Outer Harbor Wharf | 6.9 | 274.12 | 49.2 | 1.00 |
| Erzican, Turkey, 1992 | Erzincan | 6.7 | 476.66 | 95.4 | 1.00 |
| Northridge, 1994 | LA Dam | 6.7 | 564.84 | 77.1 | 1.00 |
This paper focuses on the story drift and ductility of structures governed by bending and thus the continuous cantilever column layered model (i.e. Timoshenko beam/column elements) is adopted [20]. The Timoshenko model has been widely used in the global modeling of high-rise frame-shear wall structures and shear wall structures because of its efficiency in modeling as well as little discreteness in the results [19-22]. The mass of the structure is lumped in the node. Based on the characteristics of these elements, the analysis of the whole structure is conducted through the assembly of each element. In contrast to layered models, element models provide more detailed mechanical response of elements, thus tracing the yielding and examining the failure mode of structures at the expense of huge computation cost. Different from the story hysteretic model directly defined in the layered model, the elemental hysteretic model is used in the element model to determine the stiffness of each story. The results from element models are expected to be more real and accurate than those from layered models. However, the application of the element model involves high computation cost for elasto-plastic seismic analysis of structures which is not suitable for parametric studies. The investigation on the reduction coefficient of ductility of structures conducted in this paper involves a collection of 1920 analyses and each analysis needs a large amount of iterative calculations. It is found extremely difficult and impractical to carry out so many parametric studies using the structural element model. In addition, high discreteness exists in the results from the element model. Therefore, this paper adopts the continuous cantilever column layered model to facilitate the parametric studies.
The Timoshenko beam model [18] has been widely used in seismic analysis of frame-shear wall structures or shear wall structures that are mainly governed by flexural deformation [19-22]. The lateral displacement of the Timoshenko beam model depends on the flexural stiffness in terms of α. The mathematical background and parameter of the model (Fig. 2) is briefly demonstrated as follows:
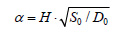 |
(1) |
Where D0 is the flexural stiffness, Do = EI, I = b3t /12 ; S0 is the shear stiffness, So = AG /1.2 ; E, G are modulus of elasticity and shear modulus, respectively; A is the sectional area, A = bt.
Mathematical background of Timoshenko-beam to simulate shear-wall structures [18].
The model structures used in this research Fig. (3b) are first configured in a typical regular vertical pattern based on current building seismic design code in China [23], and then adjusted according to different load carrying capacity for each story to obtain a vertically irregular structure. Four model buildings with 5, 10, 15 and 20 stories are used in this study to represent low-rise, mid-rise and high-rise structures, respectively, at different vibration periods. In vertically regular models, the yielding capacity of connecting elements is determined by Eq (3)~Eq(5). It’s assumed that the lateral stiffness of each connecting element is proportional to the yielding capacity of the corresponding story (Eq (6)). Based on these assumptions, it can be guaranteed that, under inverse triangular distributed load, the lateral force carrying capacity and story stiffness vary continuously and smoothly over the building height and the lateral deformed shape will be a quadratic parabola (Fig. 3a). It shows that the lateral displacement along the height of frame-shear wall structures or shear wall structures is governed by bending deformation. It can be seen that the lateral displacement is dependent on α. When α approaches zero, the deformation of structures is governed by pure bending. While for an infinite α, structures deform in pure shear. The three curves (Fig.3a) represent the deformation shape of three structures in bending, respectively, where α is generally taken smaller than 2.0. The nodes are connected by column elements with specified moment-curvature relation (Fig. 4), which uses Modified Clough hysterics model [24]. The shear deformation of the columns and the second order effect are ignored. Rayleigh damping is used to assign 5% of damping for the first two modes. The fundamental period of the structure is set equal to 0.07n (n is the number of story) by adjusting the story mass. The structure is assumed to have equal story height and mass. The story lateral stiffness is kept constant and only the yielding capacity is modified. In the Fig. (4), fy is the strength of the yield point; dy is the displacement of the yield point; dm is the ultimate displacement point. Loading sequence 1~7, and the post yield stiffness and unloading stiffness degradation parameters also show positive and negative symmetry.
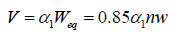 |
(2) |
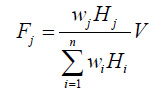 |
(3) |
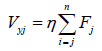 |
(4) |
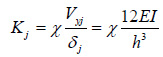 |
(5) |
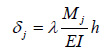 |
(6) |
Where, V is the base shear caused by earthquake;α1 is earthquake influence factor; Weq is the effective total weight of the structure; Fj is the equivalent earthquake force applied at the jth floor; n is the total number of stories; w is the weight for each floor (wi= w); I and j denote number of story; Hjis the height of node j (Hj=j·h); h is the story height; Vyj is the yielding shear capacity of floor j; Myj is the yielding moment capacity of floor j; θj is the rotation angle of floor j; η,χ and λare ratio coefficients; EI is flexural rigidity; and δj is the story drift of floor j.
Only the irregularity of the ground story strength in vertical direction is considered. The inter-story stiffness of the regular structure is kept constant and the load bearing capacity is proportionally scaled to obtain the irregular structure. The load bearing capacity of the ground story of the target irregular structure is assigned as 90%, 80%, 70% and 60% of that of the 2nd story. The capacities for the other stories remained unchanged. Based on this assumption, the capacity distribution among the stories is obtained (Fig.5). Normally, the capacity and stiffness decrease uniformly with the increasing height, as in the study of Athanassiadou [6]. In order to match the capacity distribution of buildings in reality, the capacity of each story decreases uniformly along building height. The distribution pattern in this paper is more consistent with reality compared to pattern with constant capacity distribution.
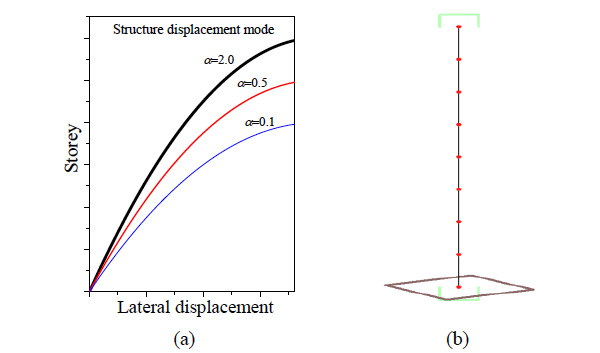
Deformation mode for systems. (a) Lateral deflected shape of flexural system. (b) Multi-mass cantilever model.
2.3. Method of Analysis
The target irregular structures have larger ductility demand than their regular structures under the same earthquake action. As the ductility demand is related to strength, we can increase the design strength (design yielding base shear or design base shear) of irregular structures in order to have the same ductility demand and ductility factor as regular structures. The base shear of the target irregular structure is determined as Eq(7). The modification coefficient of the ductility reduction factor Rir is defined as Eq(9). The modification coefficient of ductility reduction factor is the reciprocal of the magnifying factor of base shear yielding capacity. The procedure of computation is shown in Fig.(6), in which the target ductility factor is obtained in Eq(8). The average of results from 5 pulse-like and 5 non-pulse-like ground motions are obtained as the final result.
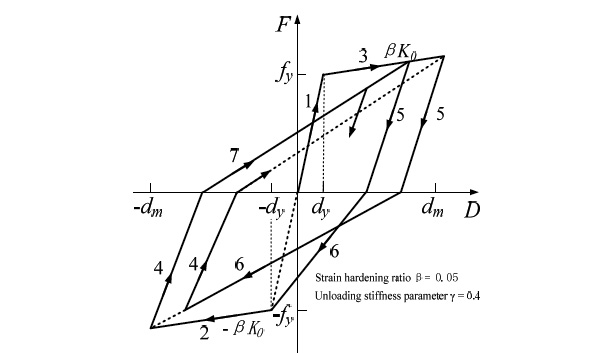
Modified clough hysteretic model.
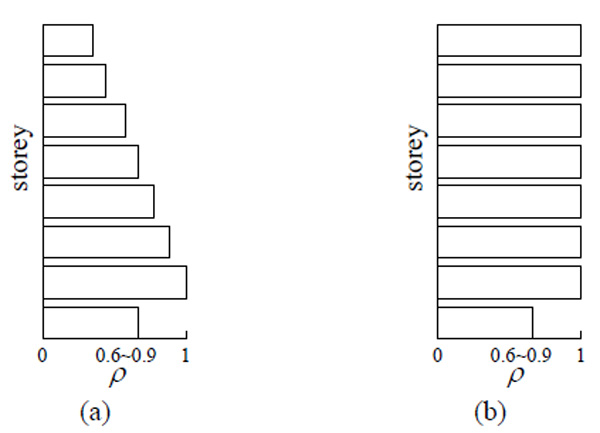
Assumed distribution of vertical irregularities: (a)in this paper, (b) as used in [6].
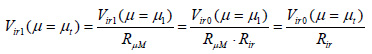 |
(7) |
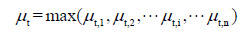 |
(8) |
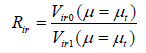 |
(9) |
Where, Vir0 and Vir1 stand for the initial and target base shear demand from irregular structures; and μ1 stands for elastic ductility demand.
Step 1, design the regular structure according to the Code for seismic design of buildings [23], and adjust the initial irregular structure by modifying the story stiffness and strength based on the analysis program.
Step 2, the dynamic time history analysis is applied to the referred regular structure using the earthquake record Qi. The target story ductility demand (μt), within a 1% tolerance error, can be obtained by adjusting the peak acceleration (PGA) of the earthquake record.
Step 3, the maximum story ductility demand of the irregular structure μMax,ir can be obtained by the dynamic time history analysis using the same earthquake record Qi and PGA.
Step 4, modify the story strength of the irregular structure to make the value of μMax,ir similar to the value of μt.
Step 5, record the ground story strength values of the regular structure and the irregular structure, and get the strength modification factor by comparison of the two values.
Step 6, Select another ground motion from Table 1 and repeat Steps 2 to 4 until all the earthquake records are used.
Time history analysis of 1920 is performed based on the following conditions: 2 types of structure models (regular ones and irregular ones), 5 pulse-like and 5 non-pulse-like earthquake records, structures with 4 different number of stories (5, 10, 15 and 20), 6 different values of target ductility demand, 4 different irregularity ratios ρ (0.9, 0.8, 0.7, 0.6). The non-linear time history analysis is performed using program Canny2010 [24].
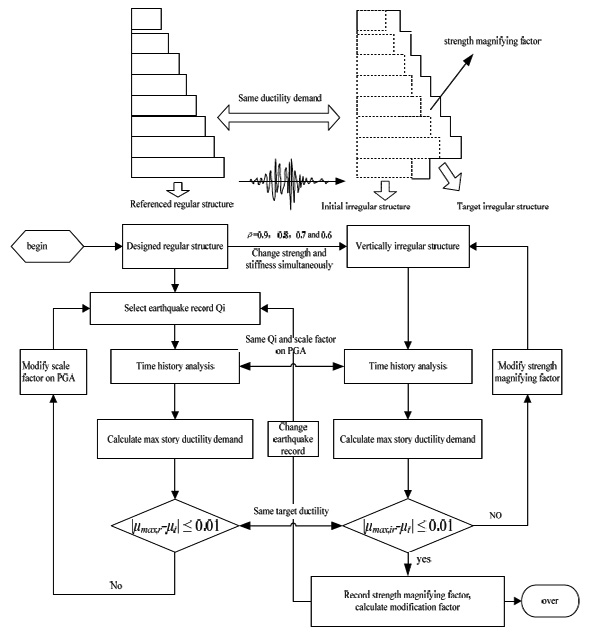
Flow chart for Rir calculation method.
3. ANALYSIS RESULTS AND DISCUSSIONS
3.1. Effect of Ductility Factor and Irregularity Ratio
Fig. (7) shows the effect of irregularity ratio of base story strength and ductility factor on the modification factor. It can be observed that the modification factor decreases as the irregular ratio becomes smaller. With smaller irregularity ratio, the structure becomes more irregular and thus more vulnerable. In order to achieve the sane target ductility demand as the reference regular structure, the yielding base strength needs to be increased. As a result, the modification factor (reciprocal of the magnifying factor of base shear yielding capacity) decreases.
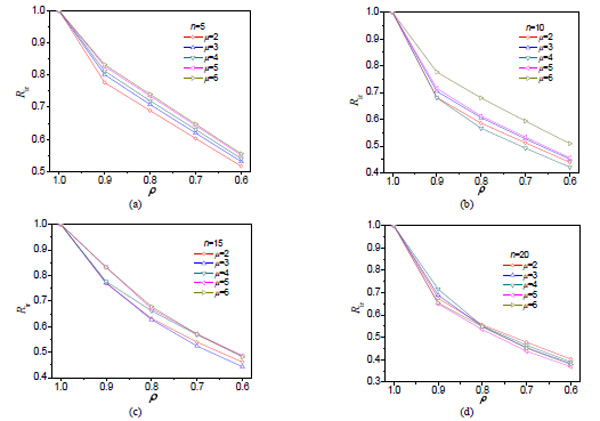
Effects of ρ and µ on Rir for pulse-like earthquake actions. (a)n=5, (b)n=10, (c)n=15, and (d)n=20.
In terms of the ductility behavior of the structure, there is no uniform trend in the variation of modification coefficient with the increasing ductility factor. For example, for the 5 story structure, the modification coefficient increases with increasing ductility demand; while for the 10, 15 and 20 stories buildings, the ductility demand can either increase or decrease. It shows that ductility demands affect the seismic behavior to some degree without an obvious trend, which deserves more study.
3.2. Effect of Pulse-like Ground Motion
In order to investigate the effect of velocity pulse in earthquake, ground motions with and without impulse contents are applied to the structures and compared their responses (Fig. 8). It can be shown that under non-pulse-like ground motions, the modification factors decreases with smaller irregularity ratio. Its variation pattern of the modification factor is similar to the situation where pulse-like ground motions are applied. However, the corresponding values are generally larger.
With the same number of story (n=15) and ductility demand (μ=3), the modification factor is smaller under pulse-like excitation than that under non-pulse-like excitation. This means that pulse-like excitations impose more demand on the structures. Under pulse-like excitation, the base shear capacity requires to achieve the same value of ductility demand becomes larger, i.e. the elastic design base shear becomes smaller.
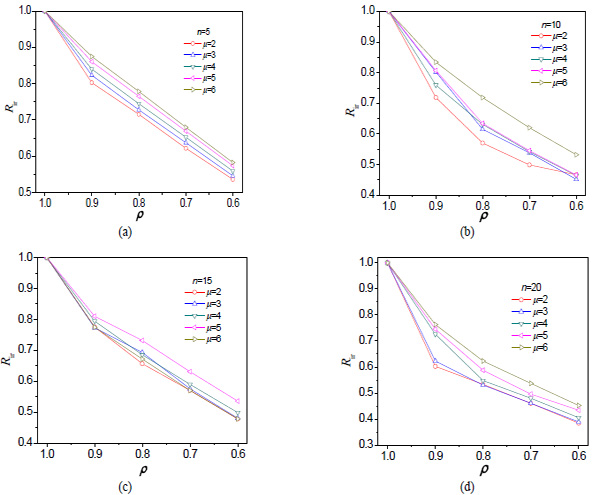
Effects of ρ and µ on Rir under non-pulse-like earthquake actions (a)n=5, (b)n=10, (c)n=15, and (d)n=20.
With smaller irregularity ratio, the modification factor coefficient is smaller, and the difference is usually larger. Fig. (9a) shows that the pulse-like excitation and irregularity ratio have a coupling effect. Under the same irregularity ratios (ρ=0.7) and target ductility demand (μ=3), the modification factor generally decreases with increasing story number (Fig. 9b), which means that the height of the building and the vibration period of the structure have some effects on the modification factor.
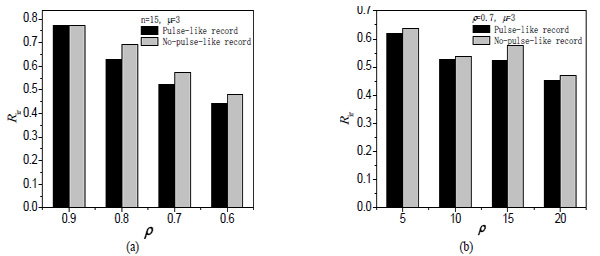
Comparison of Rir under pulse-like and non-pulse-like earthquake actions (a)n=5, µ=3 and (b)ρ=0.7, µ=3.
3.3. Comprehensive/Integrated analysis
Based on the above analysis, and neglecting the effect of ductility level, we can assess the roles of both the vertical irregularity and pulse component of earthquake in the seismic design of the buildings. Results of seismic response from 5 pulse-like and 5 non-pulse-like earthquake records are chosen to calculate the average value of modification coefficient, which are shown in Table 2 together with recommended value for engineering application. The recommended values are usually smaller than those from statistical analysis for the sake of design safety.
Statistic and suggested values and of Rir for pulse-like and non-pulse-like cases.
| Modification coefficient | Type of ground excitation | The irregularity ratios | |||
|---|---|---|---|---|---|
| ρ = 0.9 | ρ = 0.8 | ρ = 0.7 | ρ = 0.6 | ||
| Rir (statistical value) | Pulse-like | 0.75 | 0.63 | 0.54 | 0.46 |
| Non-pulse-like | 0.78 | 0.65 | 057 | 0.48 | |
| Rir (recommended value) | Pulse-like | 0.75 | 0.60 | 0.50 | 0.45 |
| Non-pulse-like | 0.75 | 0.65 | 0.55 | 0.45 | |
CONCLUSION AND SUGGESTIONS
This paper investigates the effect of irregularity of base story capacity and pulse-like ground motions on the ductility reduction factor for flexural-type system. The following conclusions are drawn: 1) Structures with vertical irregularity have larger displacement ductility demand under seismic excitation than vertically regular structure. The safety of the structure can be guaranteed by increasing the design base shear to achieve the same target ductility. 2) Structural irregularity ratio and velocity-pulse components in ground motion, having coupling effect, are the main factors to affect the modification coefficient. Modification coefficient decreases with smaller irregularity ratio; modification coefficients obtained from pulse-like earthquake excitations are smaller than those from non-pulse-like motions. To achieve the same target ductility demand, the design base shear under pulse-like earthquake is larger. Ductility levels affect the modification coefficient to some extent without following certain trend. 3) Through statistical analysis on large amount data, the statistical and recommended values for modification coefficient are given considering the effect of vertical irregularity and pulse-like earthquake. Using this modification coefficient, ductility reduction factors for vertically irregular structures can be obtained from those for vertical regular structures.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
The authors acknowledge the financial support by the Science and Technology Planning Project of Hunan in China (2014SK4062), and the National Natural Science Foundation of China (51471139 and 51071134).


