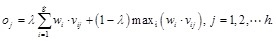All published articles of this journal are available on ScienceDirect.
Urban Planning Implementation Evaluation: A Multilevel Fuzzy Comprehensive Evaluation Approach
Abstract
Urban system is a dynamic complicated system involved with many uncertainties, thus always leading to an undesired situation that the city doesn't develop as the previously made urban plans. Urban planning implementation evaluation, which is devoted to urban planning implementation supervision and management, is an important and indispensible part of efficient, healthy and sustainable urban development. The prevailing urban planning implementation evaluation methods have been widely applied and yielded some achievement, but the existence of uncertainty definitely brings about some defects and difficulties in tradition methods. In this paper, a multilevel fuzzy comprehensive evaluation model is proposed to handle with the uncertainty and complexity in urban planning implementation evaluation. First, a multilayer comprehensive evaluation index system was established, including both conformance-based criteria and performance-based criteria. Concerning the uncertainty in the process of obtaining the dynamic criteria values, a modified analysis hierarchy process was introduced to determine the weights of criteria, fuzzy set theory was adopted to calculate the membership degrees of criteria, and different fuzzy operators were chosen to obtain the final evaluation result layer by layer. Finally, a case study was analyzed to illustrate and test the proposed approach. It is concluded that the methodology integrating analysis hierarchy process with fuzzy comprehensive evaluation is capable of dealing with the situation where criteria are complex and involved with uncertainties when evaluating urban planning implementation.
1. INTRODUCTION
Urban planning plays an important role in the process of urban development, for it concerned with comprehensive deployment of urban future development, urban rational layout, and various urban construction projects [1]. A suitable and stimulative plan has positive effects on a city in many aspects, such as efficient urban layout arrangement, well ecological and natural environment protection, rational utilization of natural resources, maintenance of social justice and fairness.
However, with rapid pace of urbanization, especially in developing countries like China, Brazil and India, the amount of cities is increasing fast, the function of city is gradually improving towards perfection, and the landscape of city is changing tremendously with each passing day. Under such circumstances, some cities may not develop in the exactly same way as the plan previously designed by the local government, leading to a waste of effort made in drawing up the urban development plans and what's worse the city may develop in an inefficient, unhealthy and unsustainable way.
Therefore, how to control the urban development to follow the guidelines formulated in urban plans is a crucial and indispensable part in urban planning. Under this situation, urban planning evaluation receives more and more attention and prosperous studies have provided insight into the theme of urban planning implementation evaluation [2-4]. However, there exists a divergence of approaches proposed in plenty studies to evaluate urban planning implementation
and they are generally categorized into two approaches : conformance-based approach and performance-based approach. Conformance-based evaluation means judging the success or failure of planning by measuring the conformance degree between the outcomes of urban development and the previously designed plan proposals. A high conformance degree indicates the implementation is well achieved and vice versa. While performance-based evaluation insists that planning is a process of decision making under conditions of uncertainty, as long as the outcomes are beneficial, departures from previous plans may be considered acceptable.
Facing the issue of urban planning implementation evaluation, no uniform approach could be adopted. Standing at different positions, scholars, planners and urban managers adopt different approaches and plenty of effort has been devoted to urban planning implementation evaluation in either conformance-based approach or performance-based approach.
As supporters of conformance-based approach, a number of researches have emerged: At the earliest, Alterman and Hill (1978) measured and examined the implementation of land use plan for Krayot area in Israel [5]; Calkins (1979) introduced a planning monitor to help the evaluation of planning as an effective means of controlling development [6]; Talen (1996) proposed methods to evaluate the implementation success of plans focusing on the distribution of public facilities [4]; Talen (1997) gave a specific example of how implementation success could be evaluated in a conformance approach [7]; Laurian (2004) presented a conformance-based plan implementation evaluation methodology to assess whether and to what degree plan policies were implemented [8]; Brody (2005) examined the spatial pattern of wetland development permits over ten years by comparing the original land use design with subsequent development activities [9]; Berke (2006) examined local plans implementation in New Zealand by both conformance and performance based-approach [10]; Chapin (2008) evaluated the implementation of local land use policies that call for limits of development in hurricane hazard zones in Okaloosa County, Florida, with the help of a parcel-based Geographic Information System [11]. On the other hand, the work of advocators of performance-based approach are briefly described as follows: Driessen (1997) addressed the performance relations between spatial planning and rural land development [12]; Lange (1997) discussed the evaluation methods of national spatial policies by their performance [13]; Faludi (2000) argued that performance-based approach is suitable for strategic spatial planning evaluation and presented the method for evaluating plan performance.
Although these studies have provided insights into the evaluation of urban planning implementation, most of them evaluate just a facet of urban development such as public facilities, land use change and wetland development, but comprehensive evaluation has not been properly addressed so far. It's generally known that an urban system is an extraordinarily complicated system, thus only one or two facets of a city are not enough to measure the implementation of urban planning. In order to evaluate the overall implementation of urban planning in a more accurate and convincing manner, the comprehensive evaluation is urgently needed.
It's a difficult task to provide a comprehensive evaluation on the overall implementation of urban planning for the reasons including tremendous amount of influence factors, multiple layers involved in even a single factor, uncertainties resulting from measurement and calculation of factors. In order to solve the above mentioned problems, we propose a multilevel fuzzy comprehensive evaluation approach, which integrates Analysis Hierarchy Process (AHP) and Fuzzy Comprehensive Evaluation (FCE), to evaluate urban planning implementation in both conformance-based and performance-based approach. The rest of the paper is organized as follows: Section 2 presents a multilayer comprehensive evaluation index system. We propose a fuzzy, multicriteria, multilayer comprehensive evaluation method in Section 3. In Section 4, we illustrate how the proposed method could be applied to evaluate urban planning implementation in Yuyao City, Zhejiang Province, eastern China. Finally, conclusion of the paper is made and future research directions are given in Section 5.
2. MULTILAYER COMPREHENSIVE EVALUATION INDEX SYSTEM
The implementation situation of urban planning can be evaluated from a single aspect such as land use change, public facility accessibility and so on. Such a single aspect evaluation is necessary in specific field to control the implementation of urban planning, however, it isn't able to reflect the overall outcomes of urban planning after years of urban development. Therefore, it is imperative to establish a systematic, comprehensive index system to make comprehensive evaluation.
To ensure the fairness, effectiveness and comprehensiveness of evaluation index system, some rules have to be followed: the index system should be found in urban development plans and be able to reflect as much aspect of the urban development as possible; the data for each indexes must be able to be collected from reliable sources and be measured and calculated by tolerable work.
According to these rules, a 4 layer comprehensive evaluation index system was designed in Fig. (1). The index system considered the overall urban planning implementation as macrolayer criterion (C) which was determined by 3 midlayer criteria: the combined index for implementation of planning objectives (C1), the combined index for spatial layout (C2), and the combined index for public satisfaction to urban planning (C3).
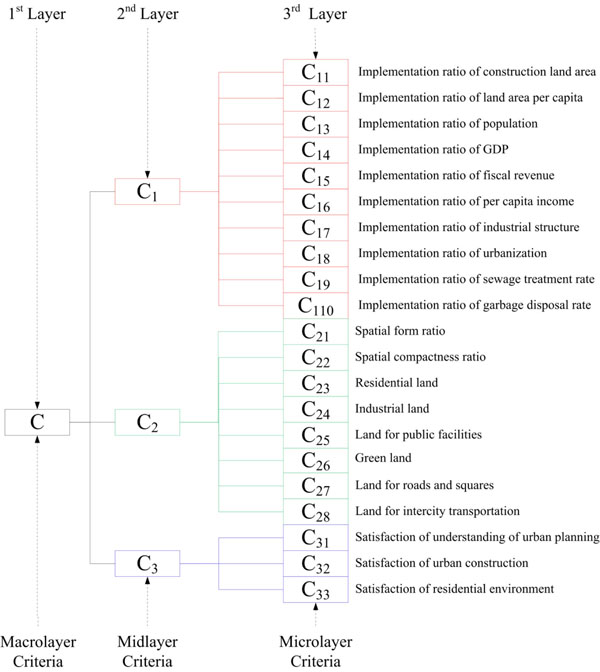
The comprehensive evaluation index system.
C1 was further measured by implementation ratio of construction land area (C11), land area per capita (C12), population (C13), gross domestic product (GDP) (C14), fiscal revenue (C15), per capita income (C16), industrial structure (C17), and urbanization (C18), sewage treatment rate (C19) and garbage disposal rate (C110), which were essential conformance-based evaluation indexes .
C2 could be decomposed into spatial form ratio (C21), spatial compactness ratio (C22), residential land (C23), industrial land (C24), land for public facilities (C25), green land (C26), land for roads and squares(C27), and land for intercity transportation (C28).
C3 was consisted of satisfaction of understanding of urban planning (C31), satisfaction of urban construction (C32), satisfaction of residential environment (C33), which were also performance-based evaluation indexes determined by public satisfaction degree.
The implementation ratios of C11, C12, … C110 and C21, C22 were computed by the criteria values of current situation divided by those of urban plans. On the other hand, since C23, C24, … C28 and C31, C32, C33 were measured in performance-based approach, the values of criteria are given by experts grading and public questionnaire surveys.
3. FUZZY MULTILAYER COMPREHENSIVE EVALUATION MODEL
Urban system is a typical complicated system, characterized by complex mechanism, ill-defined system boundaries and layers, multiple variables, and fuzziness, making evaluation of urban planning implementation a very hard task. When confronted with such problems, the core of traditional methods is to make the problem manageable by simplifying and abstracting the original problem. However, this leads to important information being overlooked, opposing viewpoints being discarded, and elements of uncertainty being ignored. In addition, information comes in different forms, both quantitative estimation and qualitative judgments [14, 15], bringing about more difficulties. Thus, a systematic methodology, which is able to handle fuzziness, multilayer, multicriteria, should be developed.
Fuzzy multilayer comprehensive evaluation model is a capable method to solve such complex problem and it has been applied in many fields such as water resources [16], network security [17], electrical system [18] and so on . AHP and FCE are integrated in the model for the weight of each criterion in the proposed multilayer comprehensive index system is determined by AHP and the comprehensive value of urban planning implementation evaluation is calculated through FCE.
3.1. Determining Weights by AHP
AHP is a systematized and hierarchical technique of qualitative and quantitative analysis used to deal with complex decisions. Based on mathematics and psychology, it was first developed by Satty [19] and has been extensively studied and refined since then [20-22]. The basic idea of AHP is to determine the relative importance through pair-wise comparison matrix after constructing a hierarchy expressed by quantification.
3.1.1. Establishment of Judgment Matrix
The judgment matrix can be described as :
 |
where aij (i = 1,2, …, n, j = 1,2, …, n) is the pair-wise relationship between criterion ai at the ith row and aj at the jth column in the same layer, which can be used to indicate the relative importance of ai and aj after their comparison. Originally, Satty proposed a 1-9 scale, in which the value of aij ranges between 1 and 9 and is limited to integer. The value aij = 1 stands for criterion i and j are equally important and aij = 9 means criterion i is extremely important than criterion j. The detailed definition and explanation of value 1 to 9 are given in Table 1 [23]. However, in many practical cases it always get into trouble for the reason that it is not easy for experts to make comparison and decide importance among as much as 9 choices in Satty's scale, so the 1-9 scale should be modified and improved to be more operable.
Definition and explanation of the value of aij in 1-9 scale.
| Value of aij | Definition | Explanation |
|---|---|---|
| 1 | Equal importance | i and j are equally important |
| 3 | Moderate importance of one over another | Judgment favors i over j |
| 5 | Essential or strong importance | Judgment strongly favors i over j |
| 7 | Very strong importance | i is strongly favored over j and its dominance demonstrated in practice |
| 9 | Extreme importance | The evidence favoring i over j is of the highest possible order of affirmation |
| 2,4,6,8 | Intermediate values between the two adjacent judgments | When comprise is needed |
| Reciprocal | Less important level | Less important level |
When the value of aij is limited to three numbers, 0, 1 and 2, it's easier to judge the relative importance between two criteria. The definition and explanation of 0-2 scale are given in Table 2 [24].By calculating the importance order index ri, where 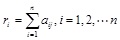 , the elements bij in the final judgment matrix Bn×n are determined by Equation (1):
, the elements bij in the final judgment matrix Bn×n are determined by Equation (1):
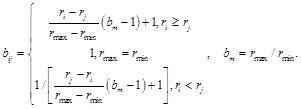 |
(1) |
Definition and explanation of the value of aij in 0-2 scale.
| Value of aij | Definition | Explanation |
|---|---|---|
| 0 | Importance of one over another | Judgment favors j over i |
| 1 | Equal importance | i and j are euqally important |
| 2 | Importance of one over another | Judgment favors i over j |
3.1.2. Establishment of Weights Set
Supposing W = (w1, w2, … wn) is the weights set of n criteria. The weights set is calculated by solving principal eigenvector of judgment matrix An×n, as shown in Equation (2):
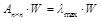 |
(2) |
where λmax is the principal eigenvalue and W is the corresponding eigenvector.
To meet the requirements that 0 ≤ wi ≤ 1, i = 1,2, …, n and 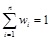 , the weight vector W have to be normalized by Equation (3):
, the weight vector W have to be normalized by Equation (3):
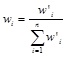 |
(3) |
where w'i is the initial element of weight vector W and is not normalized. wi is a normalized weight and could be used to calculate combined indexes directly.
3.1.3. Consistency Ratio
In order to control the result of AHP method, the consistency ratio for the hierarchy is calculated. The derivation from consistency is measured by consistency index (CI) and is calculated by Equation (4):
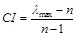 |
(4) |
where λmax is the principal eigenvalue of the judgment matrix, and n is the order of judgment matrix. The consistency ratio (CR) is used to estimate the consistency of pair-wise comparisons. The CR is computed by dividing the CI by a CI calculated from an average value over a large number of reciprocal matrices of the same order whose entries are random.
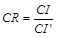 |
(5) |
The CI values of random reciprocal matrices of some frequently used orders are showed in Table 3. The closer the CR is to 0, the greater the consistency of pair-wise comparison is. When CR ≤ 0.1, the pair-wise comparison is considered to be consistent which indicating that the result is satisfactory. When CR > 0.1, the pair-wise comparison results are unreliable and the pair-wise comparison should be reconducted to improve the performance.
The CIs of random reciprocal matrices of some frequently used orders.
| Order | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| CI | 0 | 0 | 0.58 | 0.9 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 | 1.49 |
3.2. Determining Membership Degree by Fuzzy Theory
Fuzzy theory has been successfully applied in a variety of fields where uncertainties exist such as control of complex systems and expert systems. For any set X, a membership function on X is a projection from X to the interval [0, 1]. For any element x in the set X, the membership represents the membership degree of x to A, represented as A(x). When the membership A(x) is near to 1, that is to say that there is a high possibility that x belongs to A; on the other hand, when the membership A(x) is close to 0, there is a low possibility that x belongs to A. An obvious difference between fuzzy sets and crisp sets is the value of membership. In fuzzy sets, the value of membership can be any value ranging between 0 and 1, but it is limited to only 0 or 1 in crisp sets. Two curves in Fig. (2) shows the difference between crisp sets and fuzzy sets.
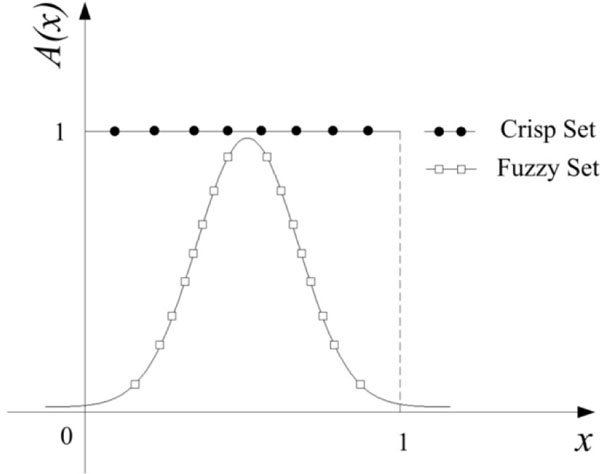
A crisp set and a fuzzy set.
Since there are many uncertainties in urban planning implementation, it's suitable to use fuzzy theory to evaluate the implementation results. Besides, membership degree can be used to describe the urban planning outcomes using the implementation levels in Table 4. In this paper, 5 implementation outcome levels, 'Very good', 'Good', 'Moderate', 'Bad', 'Very bad', are defined, so 5 membership functions are needed to calculate the membership degree corresponding to each criterion of a given value of x. The membership function A(x) is optional and could be defined according to the specific situation. For illustration, the membership functions of criterion C111, which represents the implementation ratio of construction land, are A1(x), A2(x), A3(x), A4(x), A5(x), and they are defined as Equation (6) (Fig. 3):
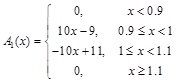 |
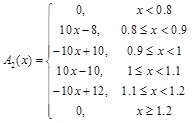 |
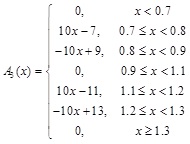 |
(6) |
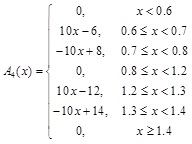 |
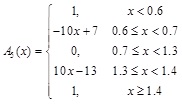 |
where x is the value of criterion C111. The membership function A1(x) is defined to calculate the membership degree of x to the implementation level Li (i = 1,2, … 5).
Assuming the implementation ratio of construction land is 0.79, the membership degrees to each level are calculated as:
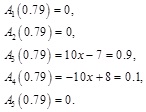 |
Relationship between linguistic variables and implementation levels.
| Implementation Level | Linguistic variable |
|---|---|
| L1 | Implementation outcome is very good |
| L2 | Implementation outcome is good |
| L3 | Implementation outcome is moderate |
| L4 | Implementation outcome is bad |
| L5 | Implementation outcome is very bad |
So, the membership vector of C111 = 0.79 to 5 implementation levels could be described as (0, 0, 0.9, 0.1, 0) as a membership vector. The obtained membership vector shows that the membership degrees of criterion value 0.79 to 'Very good', 'Good', 'Moderate', 'Bad' and 'Very bad' are 0, 0, 0.9, 0.1, 0, that is to say the evaluation result is moderate level.
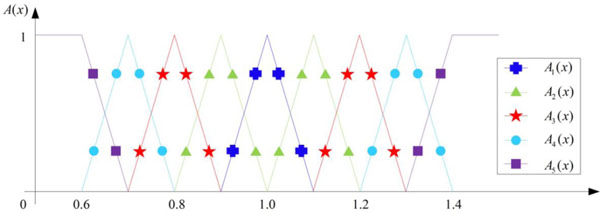
The graph of membership functions.
3.3. Fuzzy Comprehensive Evaluation
According to the fuzzy comprehensive evaluation theory, the evaluation result of urban planning evaluation can be calculated from microlayer criteria to macrolayer criteria gradually. The higher level set of fuzzy comprehensive evaluation can be obtained as follows:
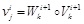 |
(7) |
where vij is the value of jth criteria in the ith layer, computed from a generalized fuzzy operation between Wki+1 and Vki+1, which are the weights set and the value set of the criteria in group k in i + 1th layer respectively. The mark ° is a generalized fuzzy operator. It's the extension of the compound operation ˅ (max) and ˄ (min) of fuzzy matrices.
Since a variety of criteria are used by decision makers to evaluate urban planning implementation, we further extend the techniques of combining fuzzy operators. The proposed fuzzy comprehensive evaluation model is able to provide an evaluation method under different rules:
For illustration , we assume that:
 |
3.3.1. Considers Every Single Factor Overall
This rule requires the inclusion of all factors that are based on the weighting coefficients. It is suitable to the evaluation in which all indexes must be accommodated. The model is
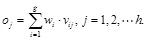 |
(8) |
3.3.2. Considers Only Those Important Factors
According to this rule, only those factors with the largest indexes determine the evaluation result. Meanwhile, the evaluation result will not be affected by the variations of the remaining factors within a certain range. It is suitable to the evaluation in which single items are emphasized. The model is
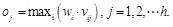 |
(9) |
4. A CASE STUDY
A multilevel fuzzy comprehensive evaluation approach to evaluate urban planning implementation with the help of GIS was presented in the previous sections. In this section, a case was chosen to illustrate and test the proposed method. The study area was Yuyao City, located in Yangtze River Delta, China. The data of urban planning objectives and current situation of study area were collected from the reference paper [25] and reorganized by authors of this paper. The pre-processed data was shown in Table 5 as the criteria values.
Criteria values and membership degrees of urban planning implementation outcomes.
| MacrolayerCriteria | Midlayer Criteria | Microlayer Criteria | Criteria Value | Membership Degree |
|---|---|---|---|---|
| C | C1 | C11 | 1.3026 | (0,0,0,0.9740,0.0260) |
| C12 | 1.1888 | (0,0.1120,0.8880,0,0) | ||
| C13 | 1.0462 | (0.5380,0.4620,0,0,0) | ||
| C14 | 1.1613 | (0,0,0,0,1) | ||
| C15 | 2.3533 | (0,0,0,0,1) | ||
| C16 | 1.4322 | (0,0,0,0,1) | ||
| C17 | 9.2:59.2:31.6 | (0,0,0,0,1) | ||
| C18 | 0.39 | (0,0,1,0,0) | ||
| C19 | 0.6 | (0,0,0,0,1) | ||
| C110 | 0.6 | (0,0,0,0,1) | ||
| C2 | C21 | 0.185 | (1,0,0,0,0) | |
| C22 | 0.215 | (1,0,0,0,0) | ||
| C23 | 70 | (0,0,0,1,0) | ||
| C24 | 50 | (0,0,0,0,1) | ||
| C25 | 50 | (0,0,0,0,1) | ||
| C26 | 70 | (0,0,0,1,0) | ||
| C27 | 70 | (0,0,0,1,0) | ||
| C28 | 50 | (0,0,0,0,1) | ||
| C3 | C31 | 3.01 | (0,0,0,0,0.0200,0.9800) | |
| C32 | 3.41 | (0,0,0,0.8200,0.1800) | ||
| C33 | 3.39 | (0,0,0,0.7800,0.2200) |
The modified AHP method was adopted to get the weight sets of different criteria. According to the 0-2 scale pair-wise importance judgment of criteria C11, C12, … C110 given by experts, the judgment matrix is obtained:
 |
Using Equation (1), the final reciprocal judgment matrix was calculated:
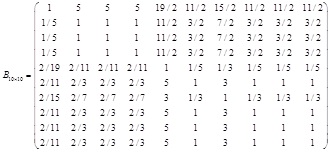 |
The principal eigenvalue λmax was 10.19, and the CI and CR were 0.0211, 0.0142 respectively. Since CR = 0.0142 < 0.1, the judgment was consistency. So the weight set of microlayer criteria C11, C12, … C110 could be calculated from the principal eigenvector using Equation (3): W13 = ( 0.3730, 0.0979, 0.0979, 0.0979, 0.0174, 0.0713, 0.0305, 0.0713, 0.0713, 0.0713 ).
The rest weight sets involved in this paper were calculated in the same way: the weight set of microlayer criteria C21, C22, … C28 was W23 = ( 0.1875, 0.1875, 0.1875, 0.1875, 0.0625, 0.0625, 0.0625, 0.0625), the weight set of microlayer criteria C31, C32, C33 was W33 = (0.2222, 0.2222, 0.5556), and the weight set for midlayer criteria C1, C2, C3 was W12 = ( 0.5242, 0.2785, 0.1973).
The membership degrees of each criterion to 5 implementation levels were computed through membership functions, which are often defined by experts according to specific situation. To illustrate the process of calculating membership degrees, the membership degrees of criterion C11 were computed through the membership functions previously given in Equation (6). The pre-processed value of criterion C11 was 1.3026, then the membership degrees to each implementation level were A1 (1.3026) = 0, A2 (1.3026) = 0, A3 (1.3026) = 0, A4 (1.3026) = 0.9740, A5 (1.3026) = 0.0260, denoted as membership vector (0, 0, 0, 0.9740, 0.0260).The membership vectors of the rest 20 criteria were calculated in the same manner, and the results were shown in Table 5.
The overall result was obtained through fuzzy comprehensive evaluation. The membership degrees of macrolayer criteria were computed through fuzzy operation between weight sets and membership vectors of midlayer criteria, which were computed through fuzzy operation between weight sets and membership vectors of microlayer criteria. The fuzzy operator adopted here was given in Equation (8) for the consideration that every single factor should be considered overall. The membership degrees of midlayer criteria C1, C2, C3 were computed as:
 |
where the maximum element in v12, v22, v32 were 0.3694 to level 5, 0.3750 to level 1 and 0.62 to level 4 respectively, indicating that C1 implementation of planning objective was very bad, C2 spatial layout was very good, and C3 public satisfaction to urban planning was bad.
The membership of macrolayer criterion C was computed as:
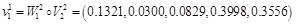 |
The final result of urban planning implementation evaluation of Yuyao City was obtained as (0.1321, 0.0300, 0.0829, 0.3998, 0.3556). The maximum membership was 0.3998 to level 4, so the urban planning implementation evaluation result obtained through the proposed method was bad, indicating that more attention should be paid to urban development to help the city to develop in a better pattern.
CONCLUSION
Urban planning implementation evaluation is one the most important tasks of urban planning. In this study, we propose a multilevel fuzzy comprehensive evaluation approach to evaluate the implementation of urban planning. The study started with setting up the multilevel comprehensive evaluation index system, which was the guarantee of a fair, effective and comprehensive evaluation. Based on the index system, a multilevel fuzzy comprehensive evaluation approach, in which the weights of criteria and overall membership degrees to different implementation levels were determined by a modified AHP and FCE, was proposed to evaluate the urban planning implementation in both conformance-based and performance-based method.
Since the evaluation index system was composed of 3 layers and each layer contains multiple subsets of criteria, the evaluation was carried out from a lower layer to a higher layer gradually and the overall result was obtained when the highest layer evaluation was finished. The modified AHP adopted 0-2 scale to describe the pair-wise judgment matrix and then transformed it to the final reciprocal judgment matrix, making it easier for experts to determine the importance of criterion and the result more reliable and convincing. The result of evaluation was calculated through fuzzy operations, which were defined in 3 types, so the selection of fuzzy operation was up to the experts according to specific situation.
The application in Yuyao City showed that the proposed framework could be applied to handle the situation where factors are involved with uncertainties and that the criteria are complex and in a large amount when evaluating urban planning implementation.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
This study is supported by the Natural Science Foundation of Hubei Province in China (2015CFA134) and the National Natural Science Foundation of China (41072199). The authors also appreciate the anonymous reviewers and academic editor for their careful comments and valuable suggestions to improve the manuscript.