All published articles of this journal are available on ScienceDirect.
Numerical Investigation of Instability of Complex Spatial Structures
Abstract
Consistent Imperfection Mode Method (CIMM) is a widely-used and effective numerical method to study the buckling capacity of spatial structure. CIMM used an “artificial” deformation instead of “artificial” load eccentricity to imitate the initial disturbance/imperfection for calculation of buckling load, and the basic mode obtained from linear buckling analysis could be used to simulate the distribution of imperfection. But in linear buckling analysis of certain complex spatial structures, the basic and first few modes usually reflect the local buckling of certain slim elements, and stability of complex structure depends on none of these local modes. Based on mode energy discrimination criterion, the improved CIMM is introduced. Improved CIMM includes following steps. 1) Normalization of all buckling modes. 2) Summarization of each mode of strain energy. 3) Discrimination of global modes with peak strain energy. 4) Based on first few global modes, CIMM could be used to calculate buckling loads respectively. 5) Choose the smallest buckling load as the buckling capacity of structure.
1. INTRODUCTION
Buckling capacity is important to soft structures such as slender pillar, slim arch and thin shell, etc. Euler first deduced a linear buckling equation of simply-supported elastic column. Perry and Robertson used imperfection to calculate the buckling load of a simply-supported elastic column. Based on Euler equation, the buckling length concept had been improved by some researchers [1]. Recent achievements about research on stability of steel frame was completed by a lot of researchers [2-5]. The buckling capacity of complex spatial structure are very difficult to identify. Imperfections in shells were studied by some researchers based on European standard [6, 7]. Chen and Shen analyzed the imperfection of Single-Layer Lattice Dome, and they developed Consistent Imperfection Mode Method (CIMM) to forecast the buckling capacity of shell structures [8, 14, 15]. Some other researchers recently studied the buckling capacity of suspendome, which is kind of a hybrid shell structure composed of spatial shell and tension cables [9, 10].
In CIMM, the basic buckling mode is defined as an “artificial” structural deformation. The “artificial” deformation is named as “imperfection of structure” to calculate the buckling load of structure. But in linear buckling analysis of certain complex spatial structures, the basic buckling mode reflects the local buckling of some slim elements. Based on local buckling mode, the buckling capacity of complex structure will be overestimated by CIMM. Only global buckling modes should be considered as imperfection distribution in CIMM. In this paper, it is explained how to determine the basic global mode and calculate the buckling loads consequently.
2. PROBLEM DESCRIPTION
2.1. Consistent Imperfection Mode Method (CIMM)
The elastic buckling load of imperfection-sensitive structure could be calculated by numerical method based onprobability theory [11-13]. But for complex structures, the linear buckling modes (distributions of imperfection) are so numerous that it is almost impossible to calculate all of them.
CIMM had been popularly used in the design and construction of spatial structures in China for decades. It is a highly effective method to forecast the buckling mode and the buckling capacity of spatial structures such as thin shells and domes, etc. The basic buckling mode was used to simulate the unfavorable initial distribution of imperfection. According to research of Chen X. and Shen S.Z [8], the maximum imperfection was defined as L/300, where L is the span of global structure. After that, nonlinear numerical analysis is performed to calculate the buckling capacity. CIMM usually consists of the following steps: FE modeling of structure, linear buckling analysis (eigenvalue analysis), identifying the shape of basic buckling mode, assuming the distribution of imperfection, imposing the imperfection on original FE model, nonlinear analysis of imperfect model. Loads applied on FE model will be increased proportionately until divergent happened in iterative calculation.
Usually, due to complexity of structures, the basic buckling mode is not the global buckling mode suitable for calculation of CIMM. The result of linear buckling analysis included a large number of local buckling modes. The perfect way could be enumeration method (complete CIMM), in which every buckling mode is regarded as structural imperfection which is used by CIMM to calculate the buckling capacity accordingly. The smallest one is the buckling capacity of this structure. It is a time-consuming work, and it is impossible to handle large-scale models in most instances.
An improved method which is based on mode energy discrimination criterion is introduced in this paper. In improved CIMM, the virtual strain energy of each normalized buckling mode should be integrated and normalized firstly. Secondly, global modes with peak strain energy are distinguished. Based on first few global modes, CIMM will be used to calculate buckling loads respectively. The smallest buckling load is the buckling capacity of structure.
2.2. Virtual Strain Energy of Buckling Mode
Based on the results of linear buckling analysis, strain energy (Δ1) of each buckling mode could be evaluated.
The virtual strain energy (Ut) of each element could be calculated by Eq. (1).
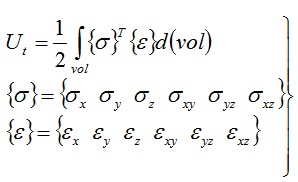 |
(1) |
Where {σ} is the stress and {ε} is the strain of the same element.
The global strain energy (Δ1) of each mode could be integrated by Eq. (2).
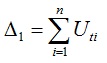 |
(2) |
Where n is the total number of elements of structure model.
2.3. Normalization of Buckling Mode and Design Criteria
In order to compare the virtual strain energy of each mode fairly, the deformation of all buckling modes should be normalized. It means that modal shape of each buckling mode should be adjusted proportionally until the maximum deformation becomes 1.0. The global mode strain energy after the normalization can be listed as Eq.(3).
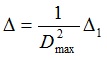 |
(3) |
Where Dmax is the maximum deformation of buckling mode before being normalized.
3. IDENTIFICATION OF GLOBAL MODE AND BUCKLING CAPACITY- EXAMPLES OF TYPICAL STRUCTURES
3.1. 2D Model 1
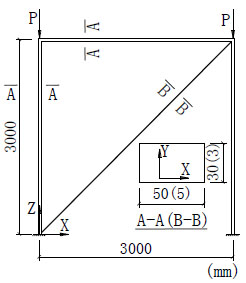
In Fig. (1), the cross-section of simply-supported Euler bar is 30mm×50mm and the weak-bracing is 3mm×5mm. The elastic modulus is 210GPa for both members. The strain energy of each calculated mode is drawn in Fig. (2) (Only the first 12 modes are shown). The shapes of these modes are shown in Fig. (3).
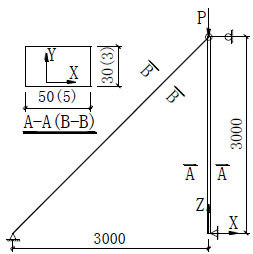
Euler bar supported by weak-bracing.
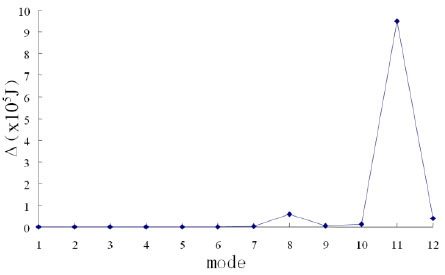
Normalized strain energy of 12 modes.
The weak-bracing is a redundant element in whole structural system. It is shown in Fig. (3) that the buckling of bracing (e.g. mode 1-7, 9, 10, 12) will not cause the collapsing of global structure. Meanwhile, the normalized strain energy of these buckling modes is much smaller than that of mode 8 and mode 11. Consequently, mode 1 to mode 7 and 9, 10, 12 could be defined as local buckling modes. Mode 8 and mode 11 should be regared as global buckling modes and their mode strain energy is significantly higher than others. Mode 8 is the basic global buckling mode. This point could be proved by the results of complete CIMM in Fig. (4).
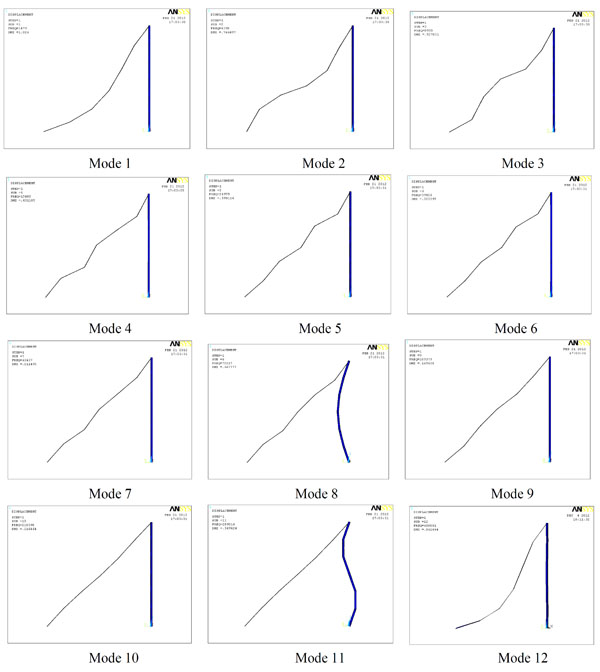
The shape of some buckling modes.
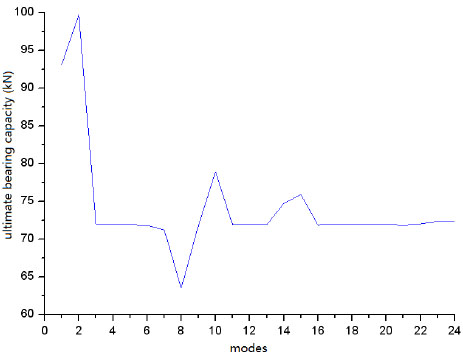
Buckling capacities of all buckling modes by complete CIMM.
3.2. 2D Model 2
Another example is a portal frame with a weak-bracing. In Fig. (5), the cross-section of main frame is 30mm×50mm and the weak-bracing is 3mm×5mm. The elastic modulus is 210GPa for both members. The strain energy of each buckling mode is drawn in Fig. (6) (Only the first 12 modes are shown). The shapes of these modes are shown in Fig. (7).
Frame supported by weak-bracing.
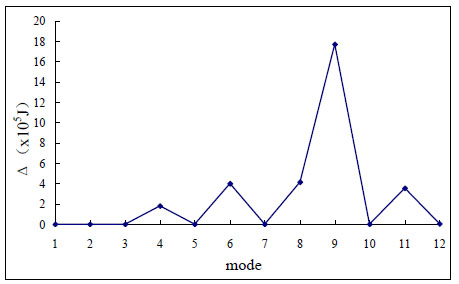
Normalized strain energy of first 12 modes.
In Fig. (7), the buckling of weak-bracing (e.g. mode 1,2,3,5,7,10 and 12) will not cause the global collapsing of portal frame. Mode 1,2,3,5,7,10 and 12 could be regarded as local buckling modes, and mode 4,6,8,9 and 11 are global buckling modes because their mode strain energy is significantly higher than others. The basic global buckling mode is mode 11, which has been proved by the calculating results of complete CIMM in Fig. (8). In particular, due to the weak-bracing’s one-way stiffness on portal frame, mode 4 is not the first global buckling mode, although its mode strain energy is the lowest in all global buckling modes (mode 4,6,8,9 and 11). That means even if all global buckling modes have been picked out, the basic global buckling mode is not necessarily the one with lowest energy.
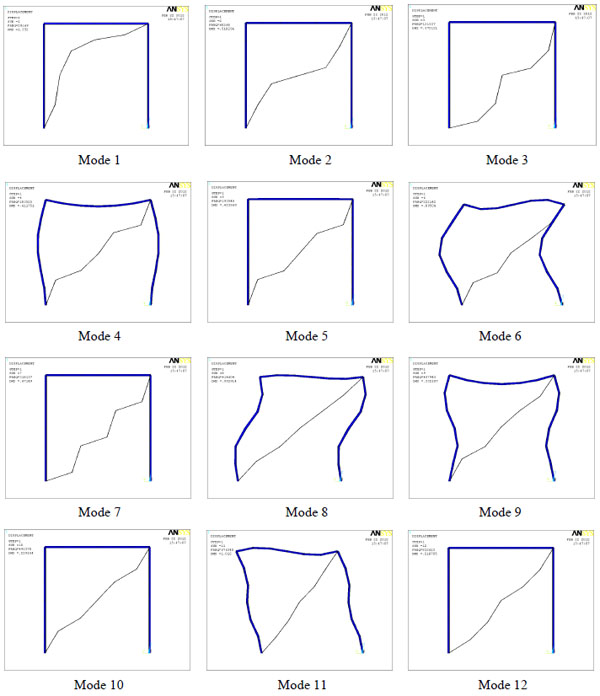
The shape of chosen buckling modes.
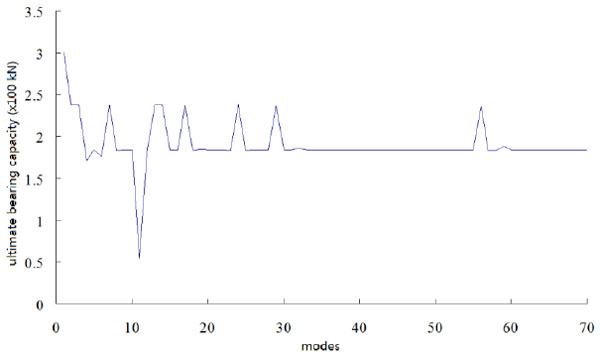
Buckling capacities of all buckling modes by CIMM.
3.3. Spatial Model 1
In Fig. (9), the meridional and zonal elements are pipes with cross-section φ 68×5.0 (which are shown as solid line) and the diagonals are φ 6.8×0.5(which are shown as dashed lines). The elastic modulus is 210GPa for all members. The initial load is uniformly distributed 1kN/m2. 1234 buckling modes are calculated, and the strain energy of first 120 of them is drawn in Fig. (10). The shapes of 4 important global modes are shown in Fig. (11).
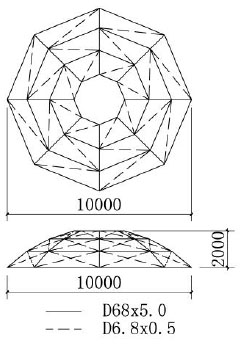
Schwedler reticulated dome.
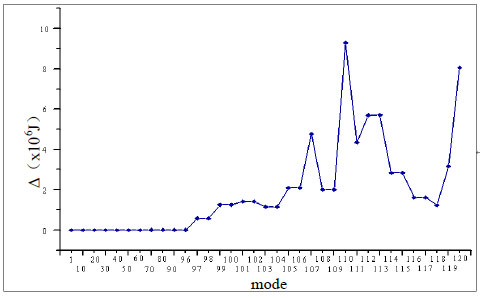
Normalized strain energy of 120 modes.
It can be found that mode 97 should be the first global buckling mode because of its sudden ascending in mode strain energy in Fig. (10). In order to verify the correctness of mode energy discrimination criterion, complete CIMM is necessary to calculate all possible buckling capacities based on all calculated buckling modes.
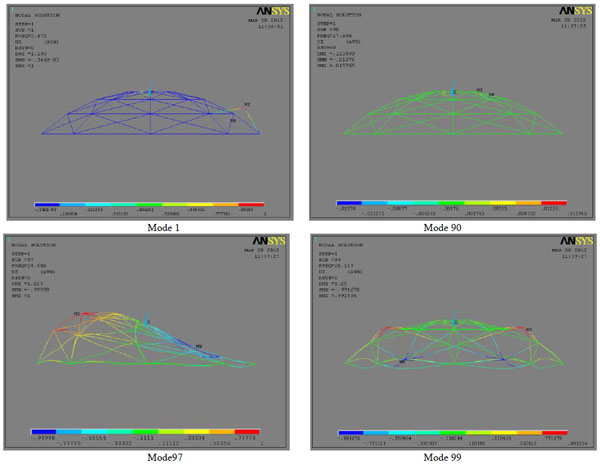
The shape of chosen buckling modes.
For spatial model 1, the buckling capacities based on all 1234 buckling modes are shown in Fig. (12), and the buckling capacities based on key buckling modes are listed in Table 1, in which UBC means the ultimate buckling capacity.
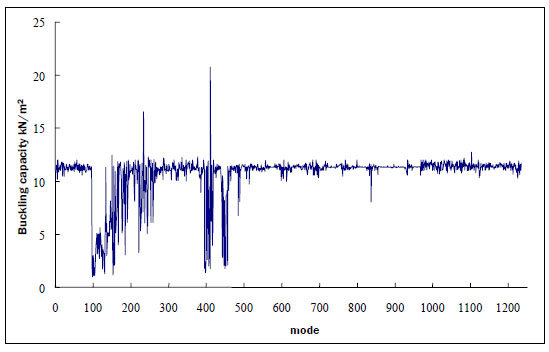
Buckling capacities based on all buckling modes.
Buckling capacities based on key buckling modes
| Mode | 1 | 30 | 60 | 90 | 96 | 97 | 98 | 99 | 100 | 101 | 103 | 117 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| UBC (kN/m2) |
10.8 | 11.4 | 11.5 | 11.4 | 11.3 | 2.05 | 1.84 | 1.00 | 3.03 | 2.63 | 1.57 | 2.72 |
Obviously, the first global buckling mode is mode 97, but mode 99 instead of mode 97 should be regarded as the basic global buckling mode of the spatial model 1 for its minimal buckling capacity. In order to find the intrinsic relation between mode strain energy and corresponding structural buckling capacity, the strain energy and buckling capacity are drawn in same diagram (Fig. 13). It could be found that there is a apparent and sudden ascending in strain energy and buckling capacity nearby the point of “real” basic global buckling mode.
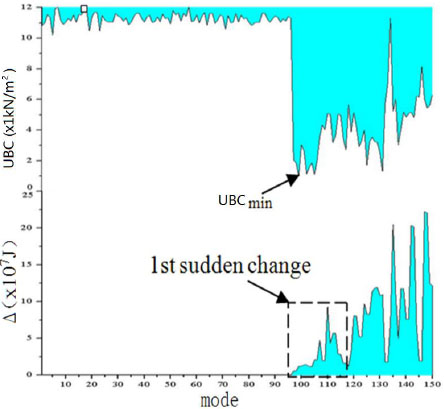
Contradistinctive diagram of buckling capacities and mode strain energy.
3.4. Spatial Model 2
In Fig. (14), the 6 members in spherical cap are pipes with cross-section φ 45×4.0 (which are shown as dashed line) and the others areφ102×4.0 (which are shown as solid lines). The elastic modulus is 210GPa for all members. The initial load is uniformly distributed 3kN/m2. The strain energy of 36 calculated modes is drawn in Fig. (15) (Only 4 of them are shown). The shapes of the chosen 4 modes are shown in Fig. (16).
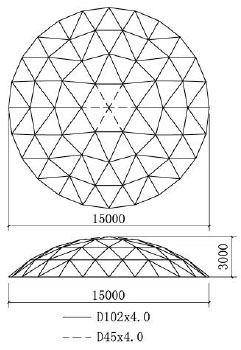
Kiewitt reticulated dome.
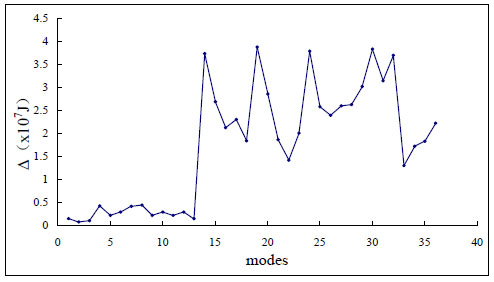
The global mode strain energy.
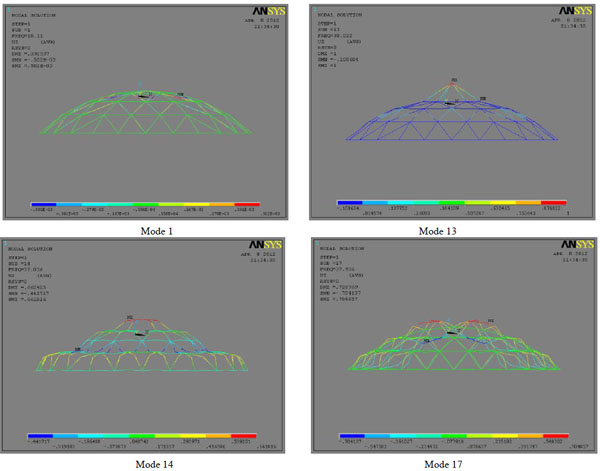
The displacement of the buckling modes.
Mode 1 to mode 13 should be regarded as local buckling modes. Mode 14 and mode 17 could probably be global buckling modes and their mode strain energy was obviously higher than others. The buckling capacities based on all 868 buckling modes are shown in Fig. (17), and the ultimate buckling capacities based on key buckling modes are listed in Table 2.
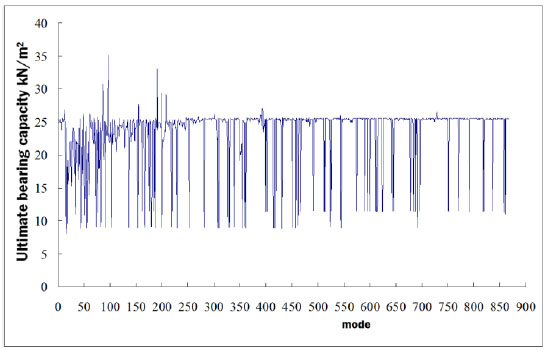
Buckling capacities based on all buckling modes.
Buckling capacities based on key buckling modes.
| Mode | 1 | 5 | 10 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| UBC (kN/m2) |
25.4 | 24.9 | 25.0 | 26.9 | 21.5 | 8.82 | 24.1 | 8.00 | 19.2 | 15.5 | 16.4 | 18.5 |
Obviously, the first global buckling mode is mode 15, but mode 17 instead of mode 15 should be defined as the basic global buckling mode of the spatial model 2 for its minimal buckling capacity.The strain energy and buckling capacity are drawn in the same diagram (Fig. 18). There is a conspicuous and sudden ascending in strain energy and buckling capacity nearby the “true” point of basic global buckling mode.
Contradistinctive diagram of buckling capacities and mode strain energy.
4. IMPROVED CIMM
Based on the above examples, improved CIMM could be developed to identify the “true” basic global buckling mode of spatial structure. There are 2 key points in improved CIMM. The first point is that the strain energy of global buckling mode is much larger than that of local buckling mode. The second point is that the basic global buckling mode is not necessarily the one with lowest strain energy, but usually is one of the lowest ones. Improved CIMM includes 2 important additional steps due to these 2 points. The first step is to calculate the strain energy of all buckling modes and draw out the diagram of energy-modes. The second step is to find out the first sudden change as (Figs. 13 and 18) in this diagram, which could distinguish global buckling modes from all calculated modes. The buckling capacity of structure is generally in association with one of the modes in the first sudden change. Hereafter, only global buckling modes in first sudden change need to be checked by original CIMM. In this way, improved CIMM becomes a well targeted and time-saving method.
5. ANALYSIS OF ENGINEERING EXAMPLE AND AUTHENTICATION
5.1. Overview on Project
A complex roof steel structure of a long-span coliseum is analyzed by improved CIMM. The model is shown in Fig. (19). The roof structure is composed of several pieces of arch-shaped trusses, which are linked to each other by diagonals. 2 main arch-shaped trusses locate in the middle of roof and span 120 meters (Fig. 20). The others are secondary trusses with smaller span (Fig. 21). The section steel of elements in main trusses is steel pipe with diameter of 351 mm and thickness of 10 mm. The section steel of elements in subordinate trusses is steel pipe with diameter of 325 mm and thickness of 9 mm. The section of diagonals is steel pipe with diameter of 168 mm and thickness of 5 mm. Elastic modulus of all elements is 210GPa with yield point of 345MPa. The dead load is 1kN/m2, which is uniformly distributed all over the roof.
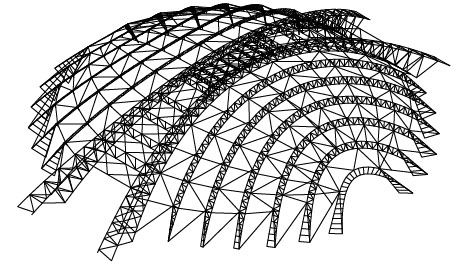
Isometric view of the global structure.
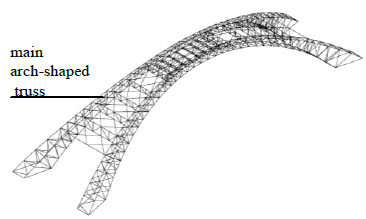
Diagram of main trusses.
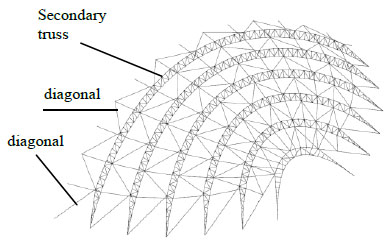
Diagram of secondary trusses and diagnals.
5.2. Identification of the Global Buckling Modes
According to improved CIMM, 1500 linear buckling modes are calculated first. The shapes of some important modes are shown in Fig. (22) and the corresponding diagram of the mode strain energy vs. modes is drawn in Fig. (23).
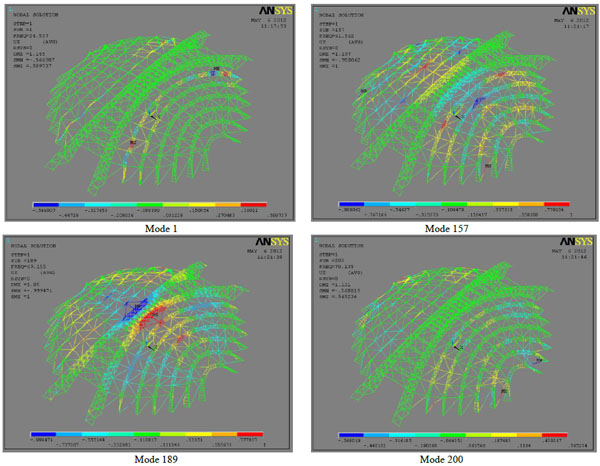
Displacement of the buckling mode.
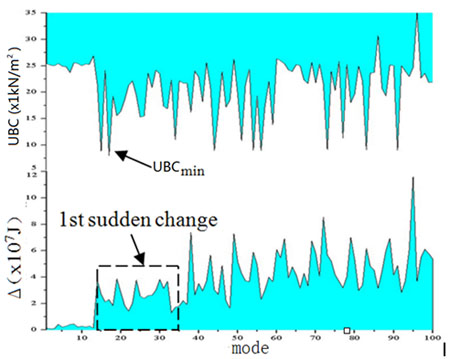
It is shown in Fig. (23) that the first sudden change is located in mode 157 to mode 200. Based on improved CIMM, only 44 modes should be calculated and checked. The basic global buckling mode could be one of these 44 modes.
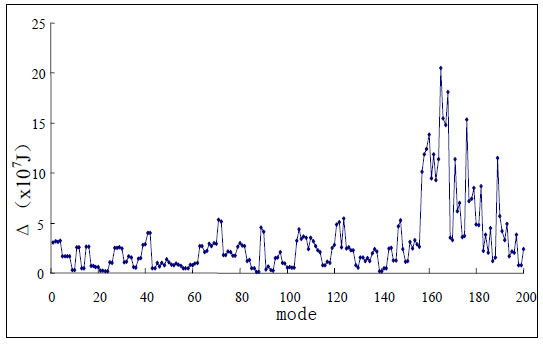
The global mode strain energy.
5.3. Verification of the Buckling Capacity and Basic Global Buckling Mode
The first 500 linear buckling modes are calculated to verify the validity of improved CIMM. The contradistinctive diagram of buckling capacities and mode strain energy is drawn in Fig. (24) The minimal buckling capacity of this structure is 8.0089, and the corresponding buckling mode is 189, which is just located within the range of mode 157 to 200. This means improved CIMM is an effective and feasible method.
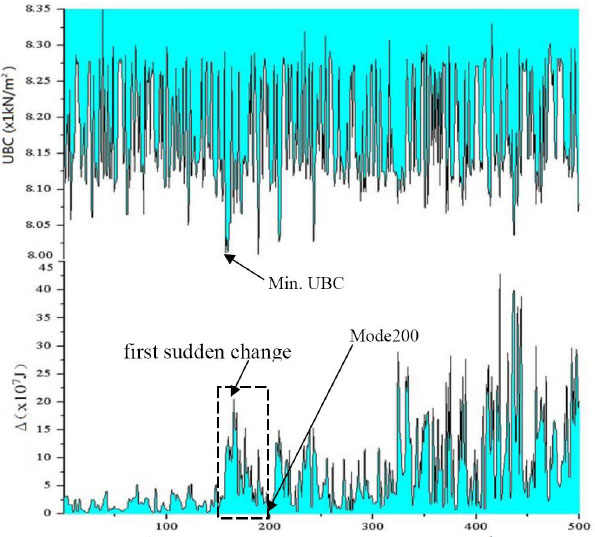
Contradistinctive diagram of buckling capacities and mode strain energy.
CONCLUSION
Consistent Imperfection Mode Method has been a widely-used and effective numerical method to study the buckling capacity of spatial structure for decades. But for certain particularly complex or uneven spatial structures, engineers have no choice but using enumeration method (complete CIMM) to obtain the correct buckling capacity. The improved Consistent Imperfection Mode Method proposed an idea to simplify the calculations. The main conclusion is listed below:
- Generally, the basic linear buckling mode has minimal normalized virtual strain energy, but it seldom becomes the global mode in complex or uneven spatial structures.
- Because local buckling modes always possess less virtual strain energy than global modes, it is convenient to distinguish global buckling modes in numerous results from linear buckling analysis.
- Even though the global buckling modes have been distinguished, the mode with lowest virtual strain energy is not necessarily the basic global buckling mode, because the buckling capacity based on this mode is not necessarily the minimal one.
- It is mandatorily required by improved CIMM to calculate the buckling capacity based on the first few global modes.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
Declared none.


