All published articles of this journal are available on ScienceDirect.
Event Tree Analysis of Xinda Oil Pipeline Leakage Based on Fuzzy Set Theory
Abstract
Event tree is a logical analysis of probability for outcome events by initiating event and probable subsequent events. However, the evaluation of every single event may contain vague information or cannot be described by a crisp number of probabilities in application. So this paper aims to develop an event tree by using fuzzy set theory with a combination of triangle membership function and trapezoidal membership function to quantify the vagueness of information and calculate the outcome probability. Through the analysis of an oil pipeline leakage accident, the method provided is fully used and the expansion of accident can be tracked through different paths of event tree.
1. INTRODUCTION
Event tree analysis is a predictive method of pipeline integration management, which is originated from the atomic field and expands to the application of chemical and engineering field in recent years [1]. It is structured from an initiating event and developed by a branch of probable subsequent events via logical language, such as Yes/No(Y/N), success/failure [2, 4]. To establish an event tree, the very first step is to choose a proper initiating event, which can be set by a comparison of several potential events and plays an important role in the following process of analysis [3]. Then each outcome event probability can be calculated through different developing paths. In the field, traditional method is to provide the crisp number of probability for each event, which demands a large amount of statistics. However, information of probability is not only affected by environmental factors but also the quality of data [5, 6]. For instance, both vagueness of information and evaluations from empirical experience could influence the data quality [7], such as multi-expert knowledge. Besides, the complexity of pipeline system, compartmentalization of structure as well as mechanism of progressive collapse from initiating event would also affect the amendment of theoretical treatment and approaches for quantifying the indices [8-10]. Therefore, there is a great call for a new qualitative analysis and fuzzy set theory is introduced to establish a bridge between qualitative analysis and probability approaches. By substituting qualitative evaluation of an event into certain fuzzy model, quantitative description can be obtained with uniform. Through de-fuzzy model, the possibility of each branch of the event tree is analyzed. This paper would focus on the development of event tree with an example of oil leakage accident based on the fuzzy model. With insufficient field data, qualitative evaluation from experts plays a significant role in analyzing the causes of event.
2. FUZZY SET THEORY
2.1. Membership Function
To deal with the uncertainties, qualitative evaluation can be transformed into membership function, which describes the variation of uncertainties. Due to the linear relation of coordinates, membership function includes many types. For the convenience of calculation, triangle membership function and trapezoidal membership function are widely used in fuzzy model analysis [11, 12]. As for triangle membership function
 , it can be shown as follows:
, it can be shown as follows:
 |
(1) |
For trapezoidal function
 , it can be shown as follows:
, it can be shown as follows:
 |
(2) |
2.2. α-cut Level
α-cut level is introduced to determine the degree of membership function. For any
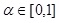 , if
, if
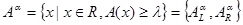 , then Aα is called the α-cut level of membership function A. In triangle membership and trapezoidal membership function, α-cut level can be demonstrated as
, then Aα is called the α-cut level of membership function A. In triangle membership and trapezoidal membership function, α-cut level can be demonstrated as
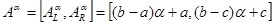 . Besides, the calculation of two α-cut level function, such as
. Besides, the calculation of two α-cut level function, such as
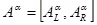 and
and
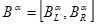 , can be shown as follows:
, can be shown as follows:
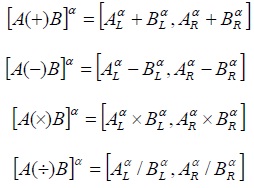 |
(3) |
2.3. De-fuzzy Membership Function
After unifying the membership function on fuzzy scale, de-fuzzification quantifies the evaluation. For traditional method, trapezoidal integration is used to de-fuzzy the membership function fL(x) and fR(x), while this paper conducts Simpson method [13] which performs high efficiency with three-order precision. The method is shown as follows:
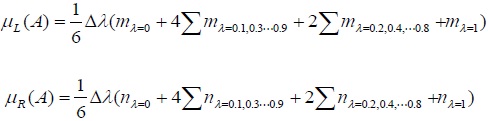 |
(4) |
Where nλ and mλ is lower and upper bound of membership function, and
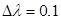 .
.
3. DEVELOPING AN EVENT TREE BASED ON FUZZY SET THEORY
Due to the absence of present data or tracking record, it is usually difficult to determine the crisp number of probability for each event, thus qualitative analysis is the only available access to describe the probability of each event, such as multi-expert knowledge based on empirical experience and present research. In order to transform the linguistic language into the fuzzy set, seven qualitative grades membership function, including triangle membership function and trapezoidal membership function, are introduced to describe the probability of each event, which is very low (VL), low (L), fairly low (FL), medium (M), fairly high (FH), high (H) and very high (VH) respectively as shown in Fig. (1).
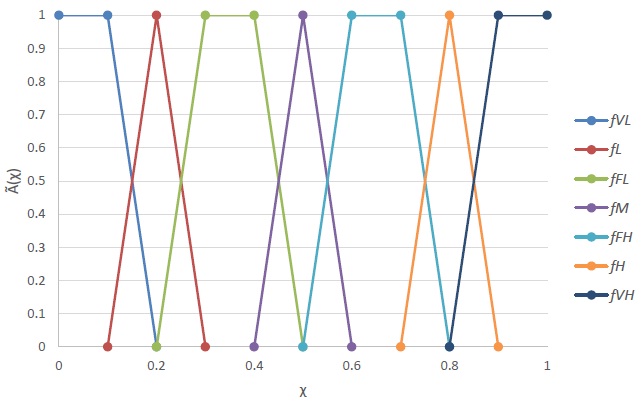
From each description for a certain event at different probability, α-cut level of membership function can be written as:
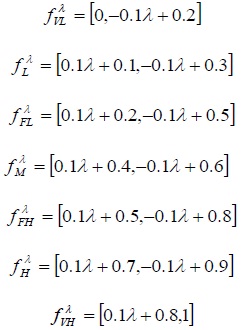 |
(5) |
For a certain event, evaluation varies depending on different expert knowledge. Therefore, based on the expertise in the field, a belief mass factor is used to weight the reliability of each expert among others. By multiplying the mass factor and probability, comprehensive evaluation for an event could be obtained, namely
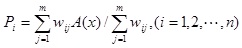 . Where Pi means the comprehensive evaluation for event i, wij means the evaluation from expert j for the event i.
. Where Pi means the comprehensive evaluation for event i, wij means the evaluation from expert j for the event i.
To determine the belief mass factor, Xie et al. [14] applies judging matrix method to analyze the fume duct fire accident, where 1 to 9 (as shown in Table 1) is used to describe the relative importance of reliability between two experts.
| Relative degree of reliability between expert i and j | aij |
|---|---|
| i and j shares the same importance | 1 |
| i is important than j | 3 |
| i is fairly important than j | 5 |
| i is rather important than j | 7 |
| i is extremely important | 9 |
| Other degrees of importance between i and j | 2,4,6,8 |
Establish the judging matrix based on Table 1, and determine the degree of reliability for each expert
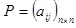 , where
, where
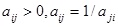 . Then calculate the average value of each row, which can be expressed as
. Then calculate the average value of each row, which can be expressed as
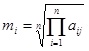 , (i = 1,2,3,.....,n), and consequently belief mass factor can be concluded as
, (i = 1,2,3,.....,n), and consequently belief mass factor can be concluded as
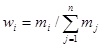 .
.
4. OIL PIPELINE LEAKAGE-AN EXAMPLE OF EVENT TREE ANALYSIS
Pipeline accidents bring huge damage not only to personnel safety but also public infrastructure and domestic economy. In 2014, the potential hazards of oil and gas pipeline in China amounts to 30,000 [15], especially the aging problem [16] of pipeline in service which aggravates the risk of accidents. Therefore, it is of great significance to motivate the pipeline integration management. For example, a typical accident happened on 30th, June 2014 along dalian Xinda pipeline of China National Petroleum Corporation (CNPC), due to the crude oil leakage. By establishing an event tree of the accident, this paper roots reasons for the accident and figures out probability of outcome event along different paths of the tree based on fuzzy set theory.
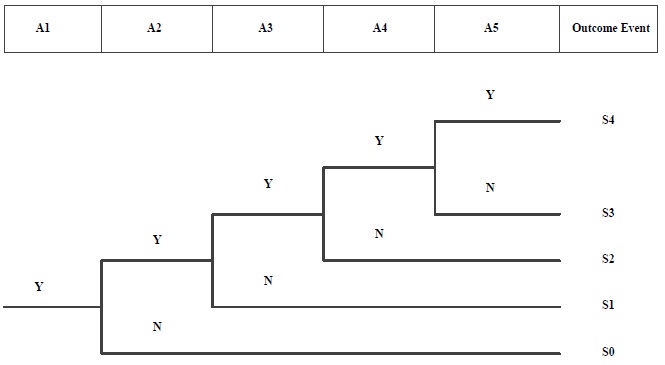
4.1. Developing an Event Tree
According to the real situation of the accident, choose the proper initiating event. Lin et al. [17] and Li et al. [18] explore potential initiating events via accident-causing theory and three basic elements of ignition, and chooses the chaos municipal construction as the proper initiating event. Based on the field investigation, the explosion was initiated between the municipal pipe and oil pipe, which could result from the chaos municipal construction and the leakage of crude oil into sewage pipe. During the explosion, the fire alert and security signals could also be a factor for efficient evacuation, or it would not cause that many deaths in record. After explosion, whether the emergence response from related departments reacted in times is doubtful. Therefore, based on the analysis, the event tree is constructed as shown in Fig. (2):
Where, A1 represents chaos municipal construction of pipeline through densely populated area, A2 represents the lack of security signals, A3 represents operation without legal permission, A4 represents crude oil invading municipal sewage pipeline, A5 represents emergency response of related department, including evacuation of the crowed.
As for the outcome events, S0 represents the potential risk of accidents due to the chaos municipal construction, S1 represents accelerating risk during construction and operation due to unidentified signals and absence of reminder, S2 represents mistaken operation on directional drilling contributing to pipeline leakage, S3 represents mutual interference between crude oil pipe and municipal pipe, which would easily form confined space and reach explosion limits, S4 represents evacuation of the crowd and elimination of potential risk which minimizes the loss of accident.
4.2. Probabilities of Outcome Events
Before determine the probability of each outcome event, we need to collect the evaluation of multi-expert knowledge about each event. Then turn the evaluation into membership function based on fuzzy set theory. In this paper, opinions are collected from five experts, who work in the multiphase flow and fluid simulation department of State Key Lab of Southwest Petroleum University with more than twenty-year field experience (expert 1 works on the leakage inspection of pipeline, expert 2 is expertise in simulation of multiphase fluid during transportation, expert 3 is the material expert for X60~X80, expert 4 focuses on integration management while expert 5 is the lab instructor for crude oil). The belief mass between each two experts is assigned with respect to their related experience. For example, expert 1 has more field experience of leakage inspection, compared with expert 2~4, so that his opinions are especially important when analyzing the municipal construction of crude oil pipeline. Therefore, compared with expert 2-4 with experience on simulation, material and management, the relative degree of reliability is assigned as 4,3,3 respectively. Then, calculate the first row as
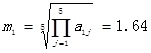 , followed by m2 = 1.25, m3 = 0.88, m4 = 0.92 and m5 = 0.60. So
, followed by m2 = 1.25, m3 = 0.88, m4 = 0.92 and m5 = 0.60. So
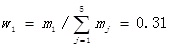 .
.
According to relative reliability of each expert, the belief mass is determined, shown in Table 2:
| Expert | 1 | 2 | 3 | 4 | 5 | Belief mass |
|---|---|---|---|---|---|---|
| 1 | 1 | 4 | 3 | 3 | 1/3 | 0.31 |
| 2 | 1/4 | 1 | 5 | 1/2 | 5 | 0.24 |
| 3 | 1/3 | 1/5 | 1 | 2 | 4 | 0.17 |
| 4 | 1/3 | 2 | 1/2 | 1 | 2 | 0.17 |
| 5 | 3 | 1/5 | 1/4 | 1/2 | 1 | 0.11 |
Based on the filed evaluation on exploded oil pipe and principle of HSE management, qualitative opinions are made. Before referring to membership function, here comes the multi-expert knowledge about each event along the event tree, shown in Table 3:
| A1 | A2 | A3 | A4 | A5 | |
|---|---|---|---|---|---|
| Expert 1 | M | L | VL | FH | FL |
| Expert 2 | M | VL | L | FH | M |
| Expert 3 | FL | L | VL | M | H |
| Expert 4 | M | FL | M | FL | FL |
| Expert 5 | FH | M | H | L | L |
For event Pλa1, the comprehensive evaluation of all the experts is demonstrated as follows:
 |
Thus,
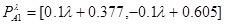
This method also goes for other events, which are shown as follows:
 |
According to Simpson calculation method, calculate the probability of each event as shown in Table 4.
| A1 | A2 | A3 | A4 | A5 | |
|---|---|---|---|---|---|
| P | 0.491 | 0.169 | 0.257 | 0.524 | 0.446 |
| PL | 0.427 | 0.166 | 0.194 | 0.438 | 0.372 |
| PR | 0.555 | 0.172 | 0.319 | 0.61 | 0.52 |
Therefore, the outcome probability can be calculated as shown in Table 5, along different paths of event tree:
| S0 | S1 | S2 | S3 | S4 | |
|---|---|---|---|---|---|
| Probability | 0.08 | 0.02 | 0.006 | 0.006 | 0.005 |
5. DISCUSSION AND ANALYSIS
Seeing from the results, probability of event A4 (crude oil invading municipal sewage pipeline) ranks the top among all the other events which accounts for 0.524, followed by the event A5 (emergency response of related department). Besides, all the outcome events belong to small probability events with each probability of less than 0.1. In accordance, the potential risk of accidents due to the chaos municipal construction ranks the top.
Tracking the failure path of Dalian “6.30” Xinda crude oil leakage of CNPC, the immediate cause of the accident is the mistaken operation of directional drilling by the construction team at the densely populated area without legal permission. However, it is because of the ignorance of potential risk as event A4, A2, A1 indicates, once the initiating event happens, the whole event soon expanded following the path A1-A2-A3-A4. Fortunately, the emergency response reacted in time and minimized the loss, the path finally follows A1-A2-A3-A4-A5.
CONCLUSION
This paper establishes an event tree analysis on fuzzy set theory and does pipeline integration management by comparing the results with the real situation of accident. In accordance with related membership function, multi-expert knowledge is quantified to calculate the outcome probability along the different paths. As the result shows, probability of event A4 (crude oil invading municipal sewage pipeline) ranks the top among all the other events, which commensurate the investigation that the explosion between oil pipe and municipal pipe in the field. Although the probability of each outcome event belongs to small probability event, the ignorance of potential risk could cause the accident, which is initiated by mistaken operation of construction team.
By analyzing the accident and emergency response of Dalian “6.30” Xinda crude oil leakage of CNPC, several conclusions can be drawn as follows:
- Prevent the accident from the source, and eliminate the factors motivating the initiating event.
- Increase the damage tolerance of the system by adding the complexity and robustness for pipeline system.
- Once initiating event happens, prevent the expansion of the subsequent events or direct the path of events to minimize the loss.
- Conduct pipeline integration management for the system in service.
- Set reasonable municipal construction plan of the network system.
- Enforce HSE (Health, Safety and Environment) management to the staffs and training before operation.
However, the event tress analysis is a predictable method to evaluate pipeline system, so that after accident happens, event tree analysis would not be predictable, while it could act as a statistical reference for setting the proper initiating event and potential subsequent events and as a comparison with the real situation.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
Declared none.


