RESEARCH ARTICLE
Low Cost Frictional Seismic Base-Isolation of Residential New Masonry Buildings in Developing Countries: A Small Masonry House Case Study
Ahmad Basshofi Habieb1, *, Gabriele Milani1, Tavio Tavio2, Federico Milani3
Article Information
Identifiers and Pagination:
Year: 2017Volume: 11
Issue: Suppl-5, M2
First Page: 1026
Last Page: 1035
Publisher ID: TOCIEJ-11-1026
DOI: 10.2174/1874149501711011026
Article History:
Received Date: 16/09/2016Revision Received Date: 02/01/2017
Acceptance Date: 03/02/2017
Electronic publication date: 29/12/2017
Collection year: 2017
open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: https://creativecommons.org/licenses/by/4.0/legalcode. This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Introduction:
An advanced Finite Element model is presented to examine the performance of a low-cost friction based-isolation system in reducing the seismic vulnerability of low-class rural housings. This study, which is mainly numerical, adopts as benchmark an experimental investigation on a single story masonry system eventually isolated at the base and tested on a shaking table in India.
Methods:
Four friction isolation interfaces, namely, marble-marble, marble-high-density polyethylene, marble-rubber sheet, and marble-geosynthetic were involved. Those interfaces differ for the friction coefficient, which was experimentally obtained through the aforementioned research. The FE model adopted here is based on a macroscopic approach for masonry, which is assumed as an isotropic material exhibiting damage and softening. The Concrete damage plasticity (CDP) model, that is available in standard package of ABAQUS finite element software, is used to determine the non-linear behavior of the house under non-linear dynamic excitation.
Results and Conclusion:
The results of FE analyses show that the utilization of friction isolation systems could much decrease the acceleration response at roof level, with a very good agreement with the experimental data. It is also found that systems with marble-marble and marble-geosynthetic interfaces reduce the roof acceleration up to 50% comparing to the system without isolation. Another interesting result is that there was little damage appearing in systems with frictional isolation during numerical simulations. Meanwhile, a severe state of damage was clearly visible for the system without isolation.
1. INTRODUCTION
Seismic isolation is an important issue for building designers in order to protect constructions from unexpected damage, particularly in regions exhibiting high risk of earthquake. Basically, earthquake is not the direct cause of loss of lives, but instead its secondary effect. Casualties appear indeed because of an inadequate seismic protection of housing or for an under-design of the structures against horizontal loads.
In developing countries, one of the common types of housing in rural areas uses masonry [1]. It consists typically of arranged clay brick bounded by mortar between. Sometimes masonry has simple columns to stabilize and stiffen the bricks walls, but it cannot be considered as making part of a resisting frame. Without a moment resisting frame, masonry houses tend to have no sufficient seismic protection to prevent severe damages and even total failure. However, to build in masonry low rise buildings is a reasonable choice for lower-class people. It is definitely cheap and easy to build. In many cases of earthquakes in Indonesia, low-class housings experienced severe damage, leading to a strong increase of casualties. Consequently, to improve the seismic resistance of low-class housings should be an issue of paramount importance for authorities, technicians involved and academics.
A practical solution to improve building resistance during earthquakes involves the installation of base isolation, which contributes in decoupling the superstructure from its foundation, to reduce the propagation of the seismic energy from the ground into the structure [1, 2]. Unfortunately, conventional isolators applied in many countries are expensive and heavy, leading to an unreasonable cost of construction. In addition, unskilled labors in rural regions would have difficulties in installing conventional isolators. Typically, conventional isolators are in the form of rubber elastomers which involve layers of rubber and steel lamina [3, 4]. That type of elastomer seems not suitable to be installed on low-class housings, due to the prohibitive cost. The other form that is cheaper is fiber reinforced elastomer (FRE), in which the fiber replaces steel lamina as vertical stiffener for the whole elastomer [5, 6]. Another attempt to reduce the cost is to focus on the elastomer and to involve recycled materials such as tyre waste [7].
Friction-based isolation is another alternative choice to reduce the cost of isolator installation. It can improve the resistance of structure by providing a sliding interface between foundation and upper structure. Thus, the energy transmission of earthquake can be fairly downgraded.
An experimental study of a small structure (prototype) based on friction isolation has been recently conducted by Nanda et al. [1]. A typical single-room residential building in India for poor persons, in masonry bricks with one door and two windows was examined (Fig. 1a). It is a common type of low-class housing in developing countries such as India and Indonesia. Before performing the structural model, properties of friction isolations were also examined through an experimental work by the authors. Four friction isolation interfaces, namely, marble-marble, marble-high-density polyethylene, marble-rubber sheet, and marble-geosynthetic were involved. Those interfaces differ in static and dynamic friction coefficient. The results of that experiment show that the frictional isolated model can reduce roof acceleration about 50% compared to the non-isolated model.
 |
Fig. (1). (a) Mounting of super structure above the plinth beam in friction isolation system during experimental work [1], (b) FE model of masonry house. |
From the researches mentioned, it can be concluded that friction isolation can significantly reduce the acceleration at roof level, leading to less damage of the masonry structure. It indicates that seismic energy propagation was certainly well isolated during earthquake. However, a disadvantage of friction isolation is that the system exhibits a permanent sliding displacement between the interfaces, requiring additional energy to restore its position. In addition, if the residual mutual displacement is large, the basic functions of the structure could be lost, with a considerable economic loss. Thus, to test the effectiveness of friction isolation it is necessary to find the optimum value of the roof acceleration and sliding displacement. According to the results [1], marble-marble interface is the most recommended interface to be applied as friction isolator and this paper is aimed at confirming or not such experimental outcomes.
2. MATERIAL AND METHOD
2.1. Friction and Materials Properties
In order to carry out a numerical investigation on low-cost base isolation, the experimental work by Nanda et al. [1] and previously discussed is adopted to carry out a study on the friction isolation through finite element (FE) simulation. As the model involves frictional interfaces, literature studies will be presented to understand suitable methods solving the frictional problems, particularly in finite element modelling. The FE model was conceived based on a macroscopic approach and the masonry material has been assumed to obey an inelastic isotropic material model. Whilst such approach can be regarded as simplistic because masonry is almost always orthotropic, several authors accept this simplification in the majority of the cases [8, 9]and, also, here attention is given more to the isolation system rather than to the superstructure. A plastic damage behavior of the masonry material by means of the Concrete Damage Plasticity model (CDP) already available in ABAQUS is adopted [10]. Parameters are determined by referring to previous investigations by one of the authors of this paper [11].
2.1.1. Friction Properties
Friction is an important phenomenon in solid mechanic, particularly in contact interfaces. Some frictional laws were developed in the past to understand the interfacial behavior of the frictional response. The most frequently used constitutive equation is the classical law of Coulomb [12, 13]. According to this law, the magnitude of the frictional force is related to the magnitude of the normal force multiplied by a wellknown coefficient called friction and its direction is always opposite to the relative tangential motion. Frictional event results into two possible situations, either (a) sliding, when Ft = μd.N or (b) sticking, when Ft ≤ μs.N, where μd is the coefficient of dynamic friction and μs is the coefficient of static friction. Those two coefficients are related to the nature of materials in contact and surface condition.
In a finite element analysis, two main methods have been developed in order to solve and simulate frictional problems, Penalty method and Lagrange multiplier method. Penalty method is the most favored method among finite element software developers due to its simplicity. In this method, the contact forces are proportional to the quantity of penetration by introducing a penalty, number which is physically equivalent to an additional fictitious linear spring between contacted bodies [14].
As mentioned above, the coefficient of friction is related to the nature of materials in contact. In the absence of direct experimental data available on such interfaces, we adopt the previous experimental work done in India [1]. Such paper provides sufficient information on the mechanical behavior of friction interfaces of all the different materials as presented in Table 1, which are implemented into the present FE model. Those materials are embedded on the two surfaces in contact between upper and bottom structure.
| Sliding Interface | Friction Coefficient |
|---|---|
| Marble-HDPE | 0.08 |
| Marble-marble | 0.09 |
| Marble-Geosynthetic | 0.11 |
| Marble-rubber | 0.16 |
2.1.2. Masonry Material Properties
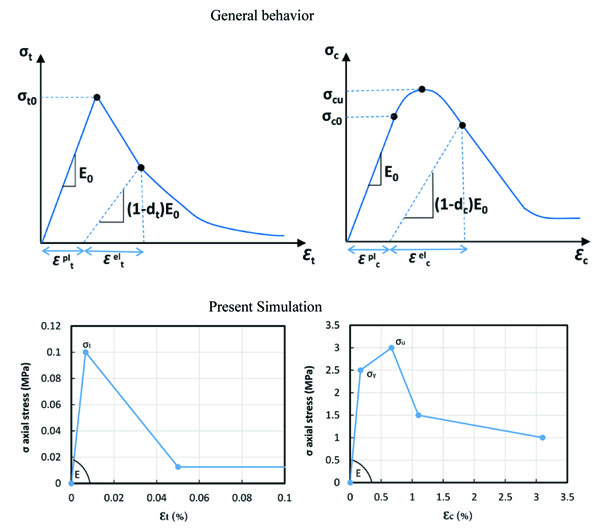
As already anticipated, in this paper we consider masonry as an inelastic isotropic material, even though in reality masonry relies into bricks and mortar joints, involving friction and low cohesion plus orthotropy. This simplified assumption leads to approximate, but still sufficiently reliable predictions of the global nonlinear behavior, as shown by many research groups in the recent past [15, 16, 8]. In this paper, a simplified concrete damage plasticity (CDP) model [17, 9] available in the commercial version of ABAQUS [18] is adopted to determine the non-linear stress-strain behavior of masonry as seen in Fig. (2). Different inelastic behaviors with softening in tension and compression can be introduced. Damage is isotropic and characterized by two independent scalars (dt and dc), which determine the deterioration of the elastic stiffness during cyclic unloading [16]. The density and Young modulus of masonry brick are 1800 kg/m3 and 900 MPa, respectively. Meanwhile, the main modeling parameters are presented and described in Table 2.
 |
Fig. (2). ABAQUS material non-linear behavior in uniaxial tension and compression. |
| Dilatation angle | Eccentricity | σb0/σc0 | Kc | Viscocity parameter |
|---|---|---|---|---|
| 10 | 0.1 | 1.16 | 0.667 | 0.0001 |
CDP model is particularly suitable for the non-linear dynamic analyses here conducted, because very accurate even under load-unload conditions [9]. It is also fully flexible in modelling the-non-linear behavior of brittle or quasi-brittle materials such as concrete and therefore for masonry bricks it adapts with great easiness.
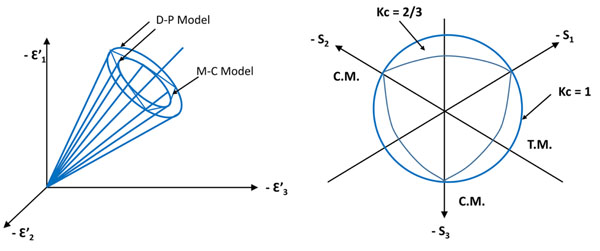
Several parameters are needed to define completely the numerical simulations that are set by referring to the aforementioned previous experimental research [17]. To determine the multi-dimensional behavior in the inelastic domain, masonry is considered to obey a Drucker-Prager strength criterion with non-associated flow rule. The strength domain is a standard Drucker-Prager surface which is modified by introducing a Kc parameter, representing the ratio between the second stress invariant on the tensile meridian and that on the compressive meridian, Fig. (3) ABAQUS modified Drucker-Prager strength domain. This parameter is determined equal to 0.667 in the FE simulations.
 |
Fig. (3). ABAQUS modified Drucker-Prager strength domain. |
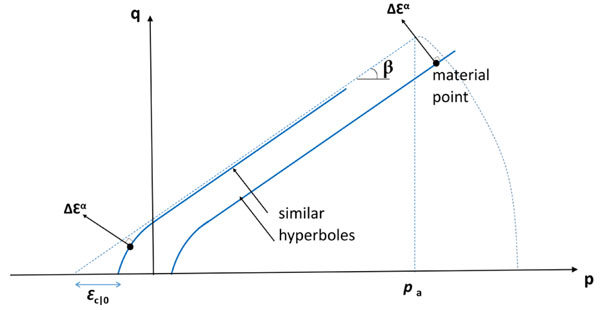
The dilatation angle is set equal to 100, which is reasonable for masonry exhibiting a moderate-to-low magnitude of compression, see Table 2. Meanwhile, a parameter called eccentricity e is introduced in order to avoid numerical instabilities. This parameter represents the gap between the points of intersection with the p-axis of the cone and the hyperbola in the p-q plane, where p is the hydrostatic pressure stress and q is the Mises equivalent stress, see Fig. (4). A value equal to 0.1 is adopted for the eccentricity parameter in the numerical simulations.
 |
Fig. (4). Smoothed Drucker-Prager failure criterion adopted in the simulation, p-q plane. |
The other parameter is a so called orthotropy ratio, which represents the ratio between the ultimate compression strength in biaxial stress states and in uniaxial conditions [14]. The parameter of orthotropy ratio is set equal to 1.16, which is a typical value from the literature.
The final stress-strain relationship in tension adopted for the dynamic analyses here presented (Fig. 2) satisfies a linear-elastic branch up to the peak stress σt0 = 0.1 MPa. Then, micro-cracks start to propagate within the material leading to a macroscopic softening. In compression (Fig. 2), the response is linear up to the yield stress σc0 = 2.5 MPa. Then, a simplified linear hardening is assumed up to the crushing stress σcu, followed by a linear softening branch. The damage variables in tension (index “t”) and compression (index “c”) are determined by means of the following standard relations:
 |
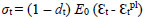(1) |
 |
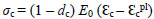(2) |
where σt, σc = uniaxial stresses; E0 = initial elastic modulus; Ɛt, Ɛc = uniaxial total strains; Ɛtpl, Ɛcpl = equivalent plastic strains; and, dt,dc = damage parameters.
It can be figured out that the compressive strength of masonry corresponds to a combination of mortar and brick strength, while in tension, the strength of masonry is more related to the mortar one, due to its very low tensile strength. Furthermore, it should be pointed out that the global damage of a structure is likely determined by tensile and shear stresses, as the compressive loads are relatively low.
3. FINITE ELEMENT MODEL
Numerical simulations are carried out by means of full 3D FE models and, as mentioned above, the masonry wall is assumed as an isotropic material with some mechanical properties fitting as close as possible after tuning the real ones. In the previous experimental work, friction isolation was introduced by plinth beam-superstructure interfaces, Fig. (1a) Meanwhile, in the present FE model, friction isolation employs the interface of two very rigid surfaces, namely the upper and bottom plate in Fig. (1b) This attempt made computation faster and easier, considering that the rigid surface will slide or stick without noticeable deformation. It seems that the frictional area in the FE model is slightly wider than that in the experimental test. This detail does not affect the final result, because the frictional force is determined only as a function of normal force and friction coefficient. The magnitude of sliding displacement will handle this issue. As long as the slip is smaller than the width of the base plinth beam in the experimental work, the model will remain on its foundation.
This study aims to examine the performance of four frictional interfaces and compare them to the model without isolation. The latter can be simplified by bonding the upper and bottom plate. Frictional properties of each interface are presented in Table 1, varying in the friction coefficient used.
The dimension of the FE model is identical to the specimen used in the experimental work, with dimension 2x2x1.5 m (length x width x height). It is a half scale one story building with door and windows opening to represent a realistic house for people with few economical possibilities. Also, the thickness of the walls corresponds to half-scale bricks (114 x 57 x 38 mm). An equivalent roof weight of about 20 kg/m2 was loaded to the top of the structure. The model was automatically meshed into around 500 eight-nodes hexahedron (C3D8R) elements (Fig. 1b) in order to speed up computations. Either the effectiveness or the suitability of the mesh method will not be discussed in this paper, but left to additional topics of the research. The emphasized issue in this study is to confirm the performance of the frictional isolator. Meanwhile, the potential future work might be how to design a technological detail of a low cost frictional isolator to be applicable on real housing.
Finally, a ground motion with 0.36 g of PGA was applied at the base plate. This magnitude corresponds to the experimental test performed in India on the shaking table. In this study, the seismic excitation applied is unidirectional and parallel to the windowed walls. During the seismic test, some indicators of an effective isolation were observed, such as for instance roof acceleration and sliding displacement, and severity of damage. The severity of damage can be monitored through the FE software by means of CDP sub-options (damage parameter) which is provided in standard ABAQUS code.
4. RESULTS AND DISCUSSION
Numerical simulations of the frictional-base isolation have been carried out. The concrete damage plasticity model and frictional interfaces (in case of isolation) seem to work well in simulating masonry under nonlinear dynamic excitation, either in isolated or non-isolated models. In the isolated model, the ground motion acceleration is dissipated by means of the frictional interface which generates a sliding displacement.
The indicators of the performance of friction-base isolation were obtained through FE simulations. Referring to the roof acceleration, Fig. (5), all of the specimens gave expected results. Roof acceleration of marble-marble interface was almost 72% smaller than specimen without isolation, Fig. (5d). A summary of all specimens is presented in Table 3. The marble-rubber interface has the worst ability to isolate seismic motion, reducing only about 27% of roof acceleration comparing to the non-isolated system. Indeed, the latter has the biggest value of friction coefficient.
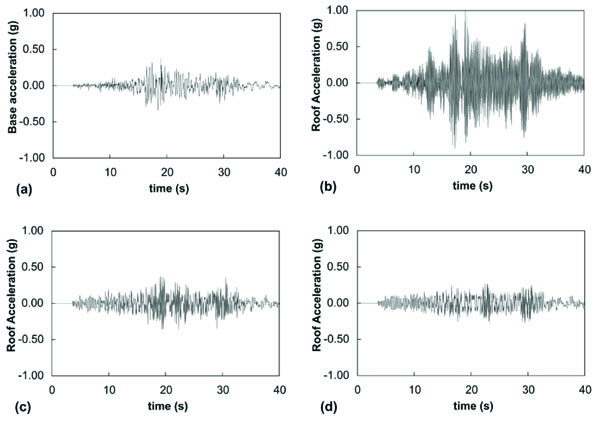
In addition, ABAQUS code is capable to present damage propagation during the seismic excitation. Damages in tension color patches at different instants are depicted in Fig. (6).
 |
Fig. (5). (a) Ground motion, roof acceleration of: (b)non-isolated model; (c) marble-HDPE model; (d) marble-marble interface. |
|
Interface |
Max Roof acceleration (g) |
Relative Sliding Displacement (mm) |
|
|---|---|---|---|
| Peak | Residual | ||
| Non-isolation | 1.03 | 0 | 0 |
| Marble-HDPE | 0.37 | 61 | 20 |
| Marble-marble | 0.28 | 80 | 30 |
| Marble-geosynthetic | 0.57 | 31 | 11 |
| Marble-rubber | 0.73 | 19 | 19 |
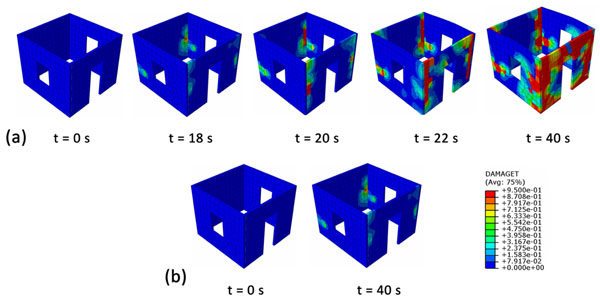
It can be seen obviously that with smaller friction coefficient, the system has better dissipative behavior. But it is not enough. To say which interface is most suitable, another parameter should be considered. That is the relative sliding displacement, which indicates whether the upper structure is falling out from its foundation. A tolerated magnitude of slip is equal to half of plinth beam width, which is 150 mm in this model. So 75 mm of slip is the maximum, exceeded that the isolator fails. In Table 3, sliding displacements of all specimens are presented. Peak sliding displacement is the maximum slip occurred during the test, while residual slip is the final sliding displacement at the end of the test. As can be seen, a system with marble-HDPE seems to perform better than all the other three specimens. That system exhibits both a 37% of reduction of roof acceleration and tolerated a sliding displacement of 61 mm, with 19 mm of residual slip. Meanwhile, even though the marble-marble system results in smaller roof acceleration, the upper-structure could not hold on the foundation, due to an out-of-range sliding displacement of 80 mm. So it can be concluded that it could not be considered a convenient device for the isolation. A comparative diagram of relative sliding displacements is presented in Fig. (7) for the sake of clearness.
In spite of evident advantages in reducing roof acceleration, the residual slip of the system becomes a drawback of this low-cost frictional base isolation. Apparently, the upper-structure has to be readjusted after every seismic motion, leading to a potential issue which is not structural but technological.
 |
Fig. (6). Tensile damage propagation during ground motion, (a) Model without isolation, (b) all models with base-friction isolation. |
 |
Fig. (7). Comparative relative base sliding displacements. |
Damage propagation on the masonry structure, which is mainly determined by the tensile damage is also depicted in Fig. (6). A severe damage can be observed at the end of the test in the specimen without isolation. Damages start from perpendicular joints of the walls and then grow mainly in vertical direction. Once the perpendicular joint is severely cracked, it could be said that the masonry structure is prone to the activation of a collapse. On the other hand, there is no noticeable (or little) damage in all specimens with friction isolation embedded. This is the most interesting outcome of the present numerical investigation.
CONCLUSION
A set of advanced finite element simulations on a small masonry prototype with frictional isolation at the base has been performed. This type of isolator is considered as a low-cost base isolator system, since it does not require any expensive attached device. Only plinth beams, attached to provide frictional interfaces between upper and lower structures, can be considered a limitation for the global deformation (especially the peak and the residual).
The results, which exhibit a good agreement with previously presented experimental data, indicate that the performance of friction-based isolation is considerably effective to isolate seismic-wave transmission into superstructure. The noticeable parameters are particularly the reduction of roof acceleration comparing to the non-isolated one and magnitude of sliding displacement. Those parameters are relatively in agreement between experimental and present numerical test.
On the other hand, residual sliding displacement can be a disadvantage for this isolation system, leading to a potential issue to be solved in next researches.
In addition, it is required to consider several other issues regarding some technological details, especially to understand if the device is easily applicable on real structures and if it can be easily removed at the end of its life.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
A.B Habieb would like to acknowledge the financial support received by the Finance Ministry of Indonesian Republic (LPDP Scholarship) for performing his PhD program at the Technical University of Milan, Italy.
