All published articles of this journal are available on ScienceDirect.
FE Modelling of Experimental Brickwork Masonry Building Under Eccentric Shear Force
Abstract
Introduction:
This paper compares theoretical results with the experimental investigation developed in the laboratory at the University of Edinburgh on a five-storey masonry building model in scale 1:3. In the case of masonry structures, unfortunately, the control of the theoretical results obtained by FE analysis is often hard although it is fundamental to verify the actual procedure of calculus both in the rehabilitation and in the project of new masonry structures.
Methods:
The aim of this work is to describe the response under lateral loading of a masonry building model prototype analysis by means of FE linear elastic modelling, assessing its performance through the comparison between the theoretical results and the experimental data. A non-linear static FE analysis has been also performed to investigate the actual ductile capacity of the structural system in relation to the different eccentricities of loadings.
Results and Conclusion:
Finally, the results of linear elastic analysis and non linear have been shown and discussed. The capacity of the ground floor’s walls of the building in shear, bending and torsional moments has been evaluated and discussed.
1. INTRODUCTION
Un-reinforced masonry (URM) buildings are quite vulnerable to earthquake damage and this has been proved by the extensive damage in the central regions of Italy in the last seismic events of 1997-98 and 2016. In particular, historical brickwork and/or stone walls have often demonstrated weakness under earthquake motions. Knowledge regarding the behaviour of masonry walls under seismic action [1-6] is however, the basis for preserving architectural heritage represented by both historic masonry monumental buildings and/or minor masonry buildings. The preservation of the architectural heritage presents different aspects due to the geometry of the structures, the variability of the materials used and the loading history of the buildings that need jet of experimental and theoretical analysis [6-9]: in particular, the shear strength of unreinforced masonry needs both of investigations, although it was analyzed over the last decades by many experimental works [1, 2, 7-9] also with different scale models [1, 10]. During the last decades, masonry wall buildings were theoretically analyzed by means of finite element method (FEM) [11-15] both linearly and non linearly. A common procedure of non linear analysis called as analysis of push-over has been adopted to study the behavior of masonry buildings subjected to horizontal static forces as representative of seismic loading. In the case of masonry structures, there is usually no need for non-linear dynamic analyses to be carried out for seismic resistance verification. Because of the regularity of a typical masonry structure, an equivalent static analysis provides reliable information regarding the safety of the building under seismic loads. In the case of non linear static analysis, the seismic resistance of the URM structures may be calculated on the basis of the assumed ultimate resistance mechanism which includes the redistribution of action to walls according to the ductility capacity. Unfortunately, the control of the theoretical results obtaining by FEM is often hard [11].
The aim of this work is to describe the response under lateral loading of a masonry building model obtained by means of FE modelling comparing the theoretical results with experimental data shown in an investigation developed at the University of Edinburgh [16] considering a static load applied with different eccentricity at the top of experimental building model. In fact, the development of computational methods of analysis, capable to describe the behavior of masonry buildings, cannot be separated from experimental studies carried out by testing the effects of shear forces, with the aim of assessing restoration techniques of historical buildings. However, detailed comparisons between results obtained by numerical modelling and experimental testing is still rather limited. It is therefore necessary to adopt an integrated approach that combines experimental and computational studies on masonry buildings, with the aim of developing more reliable procedures and methods of analysis. In this contest, experimental investigation carried out on five-storey brickwork masonry model by researchers at Edinburgh can be considered as a rare reference for validation of linear and non linear analysis by FEM.
2. MAIN EXPERIMENTAL RESULTS
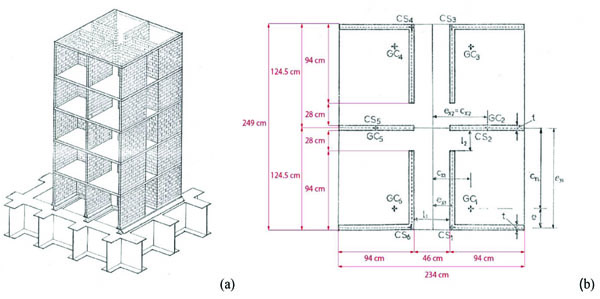
The experimental model in scale 1:3 was a five-storey masonry wall building, with a story height equal to h=965.2 mm so as the overall height was 4826 mm (Fig. 1a). Brick units measured 152.4x76.2x50.8 mm each and their mean strength fluctuated in a range from 9900 to 13016 kN/m2. A mortar mix by volume was 1:1/4:3 (cement: lime: sand) was used for mortar joints. Brick masonry Young’s modulus and Poisson’s coefficient were, respectively, equal to E=7171N/mm2 and ν=0.18 (Table 1). The model shows a double symmetric section (Fig. 1b). The thickness of the slabs at each floor was equal to 40 mm. During the tests, horizontal loading was applied by means of one hydraulic jack, placed at the upper floor in both symmetric and three antisymmetric ways (Fig. 2). Four different loading conditions where load eccentricity ei with i=0,…,3 was shifted from e0=0 to e3=1168 mm were considered during the investigation. The horizontal displacements in x and y directions were measured by a system of dial gauges, with a range of 0.01 mm, positioned near each corners of the building at all slab levels. The main experimental objective was to evaluate the structural behavior of model under horizontal load with and without eccentricity with respect to the center of the building’s symmetry. The experimental load vs. displacement diagrams were basically linear at each single floor (Figs. 6-12).
| Masonry with “Aglite” blocks | |||
|---|---|---|---|
| Young’s Modulus | E | 7.171x106 | kN/m2 |
| Shear Modulus | G | 3.039x106 | kN/m2 |
| Compressive strength | fk | 11458 | kN/m2 |
| Shear strength | fv | 150 | kN/m2 |
| Density | ρ | 1138.9 | kg/m3 |
| Poisson’s coefficient | ν | 0.18 | - |
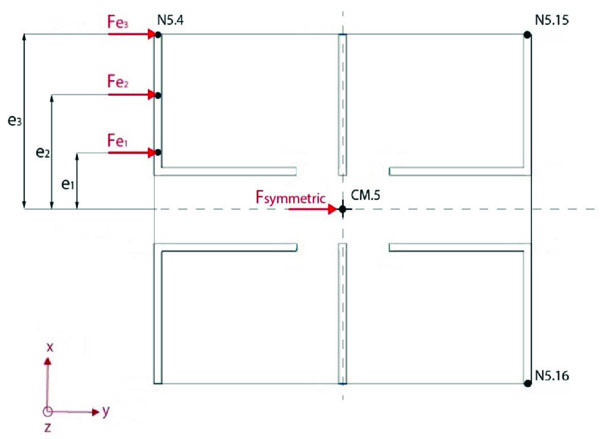
The main experimental results obtained from the experimental analysis are shown in Tables 3-9. In the Table 3 the horizontal displacement values for symmetric force F with e0=0 are contained; horizontal displacements for different eccentricities ei of load F at different points of model are listed in the Tables 4-9. All the values of horizontal displacements are given as absolute. The results are shown considering most significant vertical lines of buildings for weight point, CM.5, and borders of model, N5.4, N5.15 and N5.16 as indicated in Fig. (2).
| Step of loading | F(kN) | |||
|---|---|---|---|---|
| e=0 cm | e1=38.1 cm | e2=76.2 cm | e3=116.8 cm | |
| I | 1 | 0.75 | 0.58 | 0.38 |
| II | 2 | 1.50 | 1.08 | 0.84 |
| III | 3 | 2.27 | 1.58 | 1.40 |
| IV | 4 | 3.03 | 2.08 | 1.86 |
| V | 5 | 3.78 | 2.58 | 2.42 |
| VI | - | 4.53 | 3.08 | 2.88 |
| F (kN) | Displacements (mm x 10-2) point CM.5 | ||||
|---|---|---|---|---|---|
| floor 1 | floor 2 | floor 3 | floor 4 | floor 5 | |
| 1.00 | 1.00 | 2.75 | 4.50 | 7.25 | 10.40 |
| 2.00 | 2.25 | 5.00 | 9.25 | 13.50 | 19.50 |
| 3.00 | 3.25 | 7.75 | 13.75 | 20.50 | 29.50 |
| 4.00 | 4.25 | 10.50 | 18.50 | 27.50 | 39.25 |
| 5.00 | 5.75 | 13.25 | 22.50 | 33.90 | 49.50 |
| F (kN) | Displacements (mm x 10-2) Point N5.4 | ||||
|---|---|---|---|---|---|
| floor 1 | floor 2 | floor 3 | floor 4 | floor 5 | |
| 0.75 | 0.25 | 0.75 | 1.50 | 2.75 | 4.00 |
| 1.50 | 0.50 | 1.75 | 3.50 | 6.10 | 8.75 |
| 2.27 | 1.00 | 2.75 | 5.25 | 9.00 | 12.50 |
| 3.03 | 1.25 | 3.50 | 7.35 | 12.50 | 17.75 |
| 3.78 | 2.00 | 5.00 | 10.00 | 16.00 | 22.25 |
| 4.53 | 2.50 | 6.25 | 11.90 | 18.75 | 26.25 |
| F (kN) | Displacements (mm x 10-2) Point N5.15 | ||||
|---|---|---|---|---|---|
| floor 1 | floor 2 | floor 3 | floor 4 | floor 5 | |
| 0.75 | 0.25 | 0.60 | 0.90 | 2.25 | 3.50 |
| 1.50 | 0.65 | 1.40 | 2.45 | 4.10 | 6.75 |
| 2.27 | 0.75 | 2.00 | 3.80 | 6.50 | 10.25 |
| 3.03 | 1.05 | 2.90 | 5.25 | 8.40 | 13.75 |
| 3.78 | 1.50 | 4.00 | 7.00 | 10.85 | 17.50 |
| 4.53 | 2.00 | 5.00 | 9.00 | 13.50 | 20.75 |
| F (kN) | Displacements (mm x 10-2) Point N5.15 | ||||
|---|---|---|---|---|---|
| floor 1 | floor 2 | floor 3 | floor 4 | floor 5 | |
| 0.75 | 1.45 | 3.00 | 5.00 | 7.25 | 10.00 |
| 1.50 | 3.00 | 5.75 | 10.00 | 15.00 | 20.25 |
| 2.27 | 4.25 | 9.50 | 15.75 | 23.25 | 31.40 |
| 3.03 | 5.75 | 12.50 | 20.25 | 30.75 | 42.00 |
| 3.78 | 7.00 | 15.50 | 26.00 | 39.00 | 53.25 |
| 4.53 | 8.15 | 18.75 | 31.00 | 47.00 | 64.00 |
| F (kN) | Displacements (mm x 10-2) Point N5.16 | ||||
|---|---|---|---|---|---|
| floor 1 | floor 2 | floor 3 | floor 4 | floor 5 | |
| 0.75 | 0.40 | 0.75 | 1.25 | 2.00 | 3.25 |
| 1.50 | 1.00 | 1.85 | 3.50 | 4.50 | 6.50 |
| 2.27 | 1.50 | 2.75 | 4.50 | 6.90 | 10.00 |
| 3.03 | 2.00 | 3.60 | 6.00 | 9.10 | 14.10 |
| 3.78 | 2.40 | 4.75 | 7.50 | 11.25 | 17.75 |
| 4.53 | 2.90 | 5.90 | 9.10 | 13.50 | 21.15 |
| F (kN) | Displacements (mm x 10-2) Point N5.4 | ||||
|---|---|---|---|---|---|
| floor 1 | floor 2 | floor 3 | floor 4 | floor 5 | |
| 0.58 | 0.75 | 1.25 | 3.00 | 4.75 | 6.75 |
| 1.08 | 1.55 | 3.50 | 6.25 | 9.25 | 13.00 |
| 1.58 | 2.25 | 4.75 | 9.15 | 13.25 | 18.50 |
| 2.08 | 3.25 | 7.00 | 12.25 | 17.65 | 24.50 |
| 2.58 | 4.10 | 9.00 | 15.25 | 21.75 | 30.40 |
| 3.08 | 5.10 | 11.00 | 18.50 | 26.40 | 36.25 |
| F (kN) | Displacements (mm x 10-2) Point N5.15 | ||||
|---|---|---|---|---|---|
| floor 1 | floor 2 | floor 3 | floor 4 | floor 5 | |
| 0.58 | 0.50 | 1.50 | 2.50 | 3.75 | 6.95 |
| 1.08 | 1.25 | 3.00 | 5.10 | 7.50 | 12.75 |
| 1.58 | 2.00 | 4.25 | 7.40 | 11.15 | 17.90 |
| 2.08 | 2.25 | 5.75 | 9.60 | 14.50 | 22.50 |
| 2.58 | 2.75 | 7.00 | 11.75 | 17.75 | 28.50 |
| 3.08 | 3.00 | 8.15 | 14.25 | 21.15 | 33.50 |
| F (kN) | Displacements (mm x 10-2) Point N5.15 | ||||
|---|---|---|---|---|---|
| floor 1 | floor 2 | floor 3 | floor 4 | floor 5 | |
| 0.58 | 1.50 | 4.00 | 6.50 | 9.25 | 11.50 |
| 1.08 | 3.25 | 7.50 | 11.90 | 17.25 | 22.75 |
| 1.58 | 4.65 | 10.25 | 16.75 | 24.50 | 32.75 |
| 2.08 | 5.95 | 13.35 | 21.25 | 32.25 | 42.50 |
| 2.58 | 7.00 | 16.00 | 26.25 | 39.50 | 52.25 |
| 3.08 | 8.25 | 19.75 | 31.50 | 47.25 | 62.75 |
| F (kN) | Displacements (mm x 10-2) Point N5.4 | ||||
|---|---|---|---|---|---|
| floor 1 | floor 2 | floor 3 | floor 4 | floor 5 | |
| 0.38 | 1.00 | 1.50 | 3.10 | 4.75 | 6.75 |
| 0.84 | 2.00 | 4.00 | 7.00 | 10.35 | 15.40 |
| 1.40 | 3.00 | 7.00 | 11.75 | 17.10 | 24.25 |
| 1.86 | 4.50 | 9.65 | 15.25 | 23.00 | 32.50 |
| 2.42 | 6.00 | 12.75 | 20.25 | 30.00 | 42.25 |
| 2.88 | 7.75 | 15.75 | 25.00 | 36.25 | 51.00 |
| F (kN) | Displacements (mm x 10-2) Point N5.15 | ||||
|---|---|---|---|---|---|
| floor 1 | floor 2 | floor 3 | floor 4 | floor 5 | |
| 0.38 | 0.60 | 1.75 | 3.00 | 4.25 | 5.75 |
| 0.84 | 1.25 | 3.10 | 6.10 | 9.00 | 12.75 |
| 1.40 | 1.75 | 5.00 | 9.50 | 14.50 | 20.75 |
| 1.86 | 2.50 | 6.75 | 12.75 | 19.00 | 27.75 |
| 2.42 | 3.25 | 8.90 | 16.25 | 25.00 | 36.00 |
| 2.88 | 4.00 | 10.90 | 19.75 | 30.25 | 42.75 |
| F (kN) | Displacements (mm x 10-2) Point N5.15 | ||||
|---|---|---|---|---|---|
| floor 1 | floor 2 | floor 3 | floor 4 | floor 5 | |
| 0.38 | 1.50 | 3.25 | 5.00 | 7.50 | 8.75 |
| 0.84 | 3.00 | 7.25 | 11.25 | 16.50 | 21.25 |
| 1.40 | 4.60 | 11.00 | 18.00 | 27.25 | 34.50 |
| 1.86 | 6.25 | 15.00 | 24.00 | 35.75 | 46.00 |
| 2.42 | 8.00 | 18.75 | 30.75 | 45.75 | 59.50 |
| 2.88 | 10.00 | 23.00 | 37.50 | 56.00 | 71.40 |
| F (kN) | Displacements (mm x 10-2) Point N5.16 | ||||
|---|---|---|---|---|---|
| floor 1 | floor 2 | floor 3 | floor 4 | floor 5 | |
| 0.38 | 0.50 | 0.90 | 1.50 | 2.25 | 3.50 |
| 0.84 | 0.70 | 1.25 | 3.00 | 4.50 | 5.75 |
| 1.40 | 1.00 | 2.65 | 4.75 | 7.25 | 8.90 |
| 1.86 | 1.50 | 3.75 | 6.50 | 9.50 | 11.50 |
| 2.42 | 1.75 | 4.60 | 8.25 | 12.00 | 14.50 |
| 2.88 | 2.25 | 5.50 | 9.75 | 14.50 | 17.75 |
Experimental diagrams confirmed that torsional displacements and rotations may be neglected in case of buildings characterized by structural symmetry and symmetric load conditions. Therefore, the hypothesis that flexural bending displacements may be evaluated separately from torsional ones is reliable and experimentally assessed in many cases where masonry buildings are characterized by a regularity in the disposition of the walls in plan and elevation.
3. MATERIALS AND METHODS
3.1. FE Modelling and Method of Analysis
In this section, numerical modelling of the in scale five-storey masonry building tested under eccentric lateral loading is presented. The scope has been to create a FE model that can approximate adequately the experimental behaviour of the masonry structure and recognize the torsional effects recorded in the tested building.
Masonry is a material that exhibits distinct directional properties due to the mortar joints.
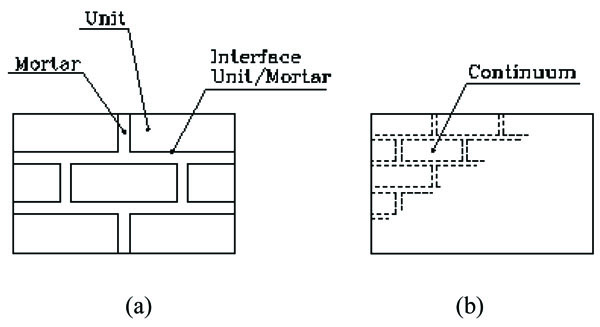
In general, the approach towards its numerical representation can focus on the micro-modelling of the individual components, unit and mortar, or on the macro-modelling of masonry as a composite (Figs. 3a and b).
In the first approach, Young’s modulus, Poisson’s ratio and, optionally, inelastic properties of both unit and mortar are taken into account. However, an accurate micro or macro-modelling of masonry requires experimental knowledge of materials (Table 1). The behaviour of said building was analysed by theoretical FE modelling with different linear and non-linear procedures, considering the macro-modelling approach and assuming finite plane elements.
Finite element code Sap2000 with non linear elements was adopted. First of all a non linear material was defined in order to reproduce the mechanical characteristics of the experimental model. The constitutive law was determined considering Young’s modulus and ductile capacity of masonry; in order to consider the non linearity of constitutive law, an elastic-perfectly plastic bilinear stress-strain relationship was employed; according to the Mohr-Coulumb criterion, the friction angle was defined as 21.8°. Bidimensional non linear layered shell elements have been chosen to model the brickwork masonry panels. The chance to define a shear bond with cohesion and friction coefficients makes the shell layered element appropriate for the numerical modelling of masonry walls, with the correct assignment of the non linear features of material. Besides, the geometry of masonry walls was modelled by a bidimensional elements mesh (Fig. 4a), characterized by a thickness of 5 cm, as indicated in the experimental study. Finally, fixed constraints were modelled at the bottom of the walls of the ground floor (Fig. 4b).
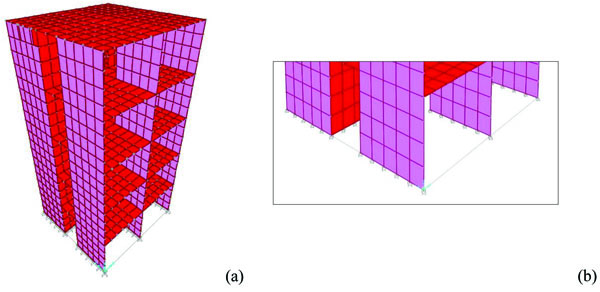
Initially, a 3D model, considering each reinforced concrete slab as a rigid floor, has been studied. Diaphragm constraints, which allow no relative displacements between joined nodes, were used to represent the infinitive stiffness of each floor. It is evident that this simple model provides an excessive stiffness in all loading conditions, so it is far from predicting the experimental displacements. The hypothesis of perfect rigid floor causes a stiffer FE model than the experimental prototype. Deformable shell-thin elements, characterized by a thickness of 40 mm, have been chosen to represent the reinforced concrete slabs.
The numerical analysis has been developed increasing horizontal force applied both axially, through the shear centre of system, and eccentrically at the top slab level of the structure.
During the test, static horizontal loading was applied at the upper floor as shown in Fig. (2) with different steps of loading applied at different eccentricities ei with i=0,…,3 (Table 2).
The FE static analysis has been performed considering both elastic and post-elastic behaviour. The results of numerical analyses were compared with the experimental data. The nonlinear analysis were performed in order to analyse the effect of load’s eccentricity on the structural behaviour of multi-storey masonry building until failure and non linear capacity diagrams were defined.
A preliminary analysis of the dynamic response of the multi-storey masonry building was performed by defining free-vibration periods (Fig. 5), frequencies and mode shapes. Modal analysis was implemented considering 15 mode shapes, 3 for each floor. Results show that mode shapes of low-order mathematical expression tend to provide the greatest contribution to structural response, in terms of natural periods and effective modal masses. The first mode has shown a torsional mode shape characterized by a period of 0.085 sec and a modal participating mass ratio of 69%; instead, the other two vibrational modes have exhibited purely translational mode shapes in X and Y directions with periods of 0.082 sec, equal to each other. These modes got respectively 71% and 68% of the modal mass participating ratio. The fourth mode was characterized by a period of 0.022 sec and a low value of the modal mass participating ratio (i.e. 18%). As orders increase, mode shape contributes less in terms of period and modal mass participation; probably, this is due to the characteristics of the structural system, which presents horizontal and vertical regularity.
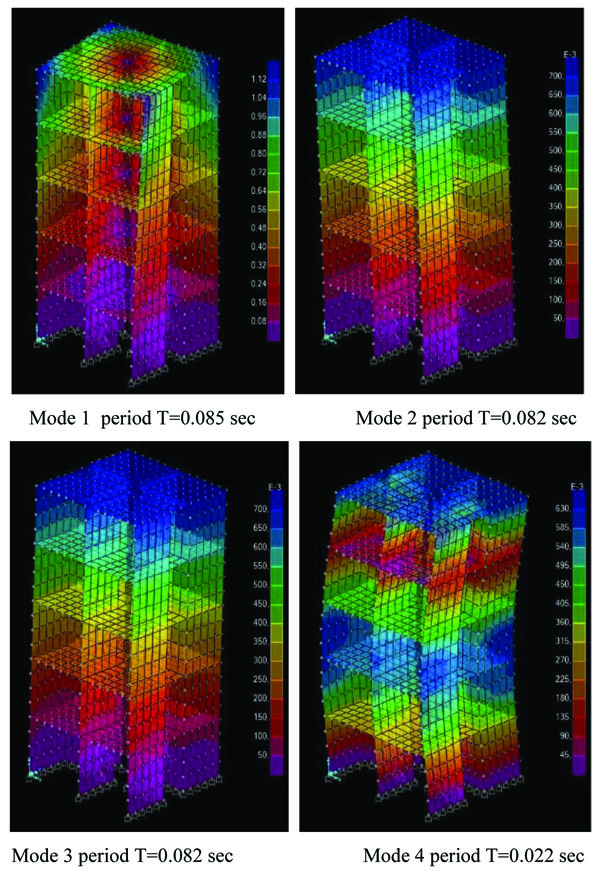
The experimental analysis and the results previously described in the structural behaviour of the model under static loads are characterized by flexural horizontal displacements at each floor; in particular, torsional displacements are not found when the load is symmetrically applied. The modal analysis evidences on the other end the torsional effect showing the eigenform as the dominant one.
Results of non linear static analysis have provided insight into the ductile capacity of the structural system, and they have indicated the mechanism, load level, and deflection at which failure occurred. The non linear analyses were carried out until a phase where the response of damaged structure was no longer proportional to the applied loading. Therefore, the five-storey masonry model was subjected to a gravity loading and a monotonic displacement-controlled lateral load pattern applied at the top floor, which continuously increased through elastic and inelastic behaviour until an ultimate condition was reached. Outputs generated static-pushover curves, which plotted strength-based parameter against both the lateral displacements and rotations of a control point at the top of the structure.
4. RESULTS AND DISCUSSION
4.1. Comparison of Results
A discussion on the comparison of experimental and numerical data obtained analysing the linear behaviour of the five-storey masonry building is developed below.
Reasonably good agreement has been found between the linear elastic analysis and experimental results. The linear FE theoretical model proves to be capable in capturing the structural behaviour of the tested brick masonry building; both horizontal displacements and rotations have been in good agreement with the experimental results in all loading conditions (Figs. 6-12).
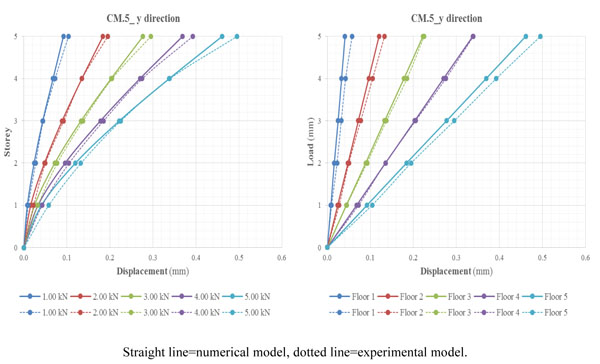
It is evident that the load case characterized by symmetric loading provides results in reasonable agreement with the experimental data. The comparison between experimental and theoretical storey/displacement and load/displacement diagrams for each floor, at various load values, shows partial overlaps. It is possible to see that the displacements calculated by the FEM are often underestimated and the numerical model seems to be stiffer than the tested building. The FE model seems not subjected to rotations and presents a maximum displacement of 0.5 mm at the top for F=5.0 kN, in agreement with the experimental case (Fig. 6).
Analogously, even for the eccentric loading conditions, the results of numerical model are confrontable in terms of displacements and rotations with experimental data. Also for these cases, the theoretical results have been still undervalued respect to the experimental data; this is probably due to the presence of a fixed constraint condition in the numerical model that was difficult to reproduce in laboratory conditions at the time of the experimental study.
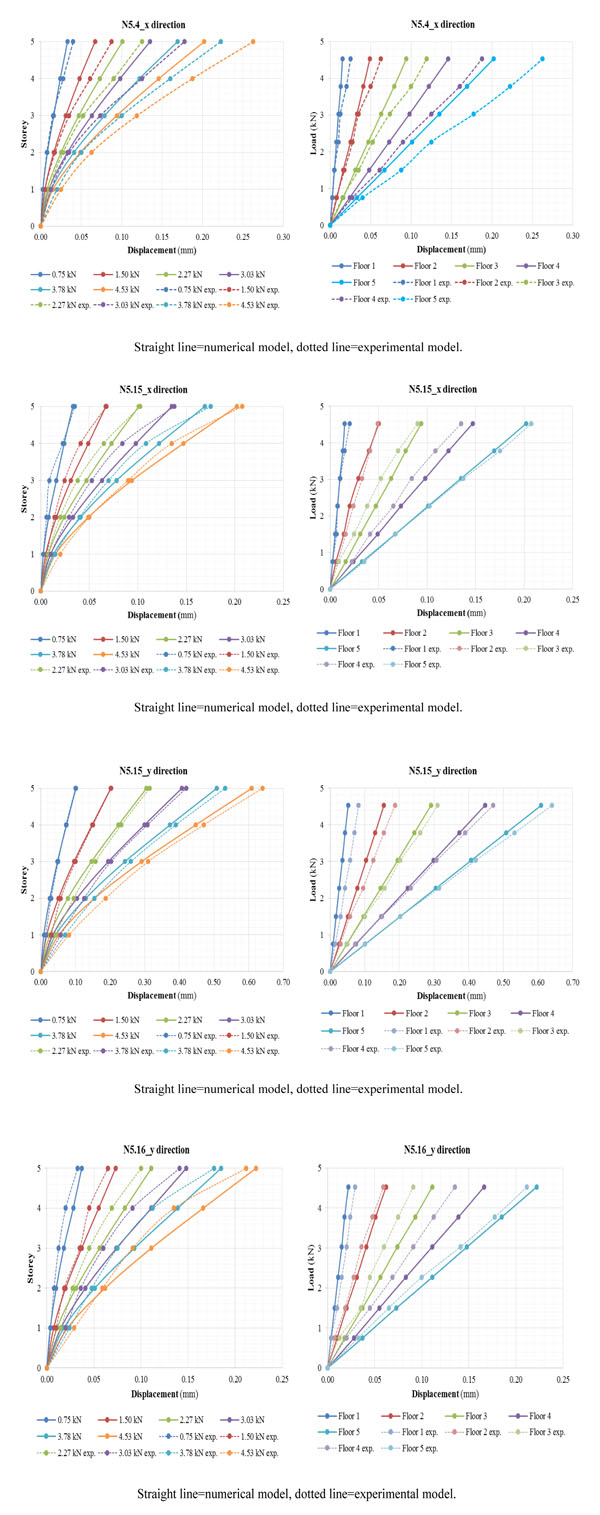
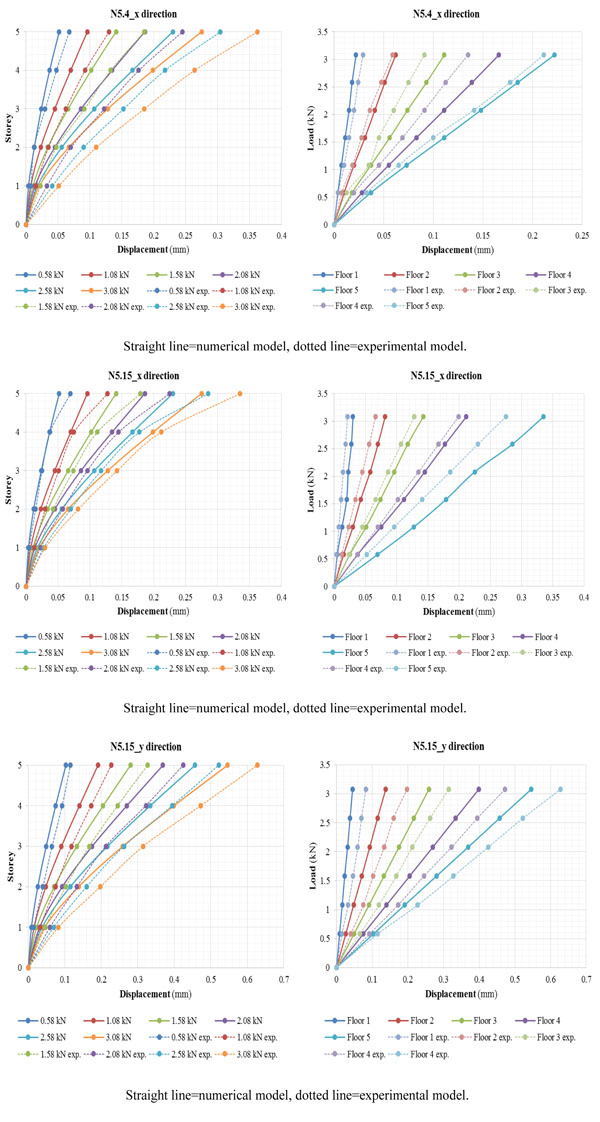
The results of the linear analysis for the eccentric loading e1 are given and compared with the experimental data in Fig. (7). It can be seen that they are in good agreement in each loading steps. Considering the control point N5.15, the maximum displacement in the X direction is equal to approximately 0.2 mm. For the Y direction, parallel to the direction of the load application, it can be noted that the numerical modelling appears to approximate the experimental results correctly with a value of displacement of about 0.609 mm. Comparing the displacement recorded at the control point N5.16 in the Y direction between the theoretical and experimental diagrams, it can be seen that there is a low torsional motion of the building although the eccentricity of loading is small. In fact, the value of displacements in this point is significantly lower, equal to about 0.222 mm, and comparable with that observed in the X direction at the control point N5.15.
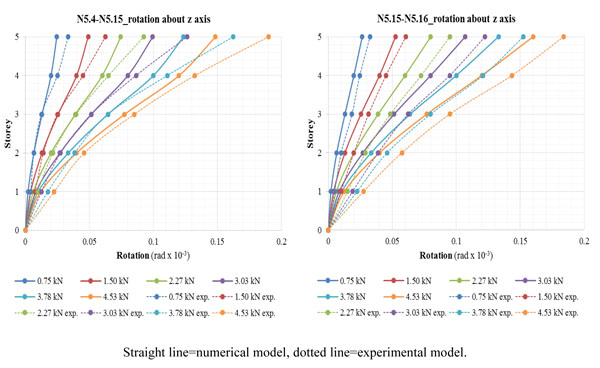
Rotations, expressed in rad*10-3, were averaged at the nodes N5.4/N5.15 and N5.15/N5.16; this procedure was done for carrying out the comparison between numerical model and experimental study. The averaged values of rotations exhibit low standard deviation values, so the extrapolated data are statistically significant and entirely comparable. A comparison is made in Fig. (8) between the numerical and experimental curves storey vs rotation for structure at various loading. Therefore, it is possible to notice that the maximum rotation, obtained by averaging the values of nodes N5.4 and N5.15, is equal to about 0.149 rad*10-3. Instead, at the nodes N5.15 and N5.16, the maximum rotation is slightly bigger than the previous, with a value of 0.160 rad*10-3.
Referring to the results of the linear analysis for the eccentric loading e2 contained in Fig. (9), it can be noted that, in the case of measurement at control point N5.4 and N5.15, the eccentric loading caused displacements in the X direction mainly higher than observed in the previous load case with eccentricity e1, although the load path had a lower value. In fact, the maximum displacement of the control points N5.4 and N5.15 in the X direction is equal to approximately 0.275 mm. Instead, for the Y direction, it can be seen that the numerical modelling provides results that are found to be lower than the values observed for the eccentric loading e1, with a maximum value of displacement at the top of about 0.546 mm.
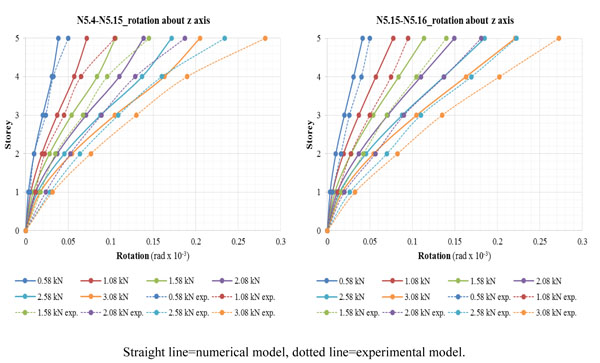
A comparison between the storey/rotation curves in the case of eccentric loading e2 Fig. (10) highlights that higher eccentricity has led to major rotations than before. Referring to the control points N5.4 and N5.15, it can be noted that the applied loading has produced a maximum value of rotation equal to about 0.205 rad*10-3. Furthermore, analogous result has been obtained by averaging the values at the control points N5.15 and N5.16, where it is possible to notice that the maximum rotation is equal to about 0.221 rad*10-3.
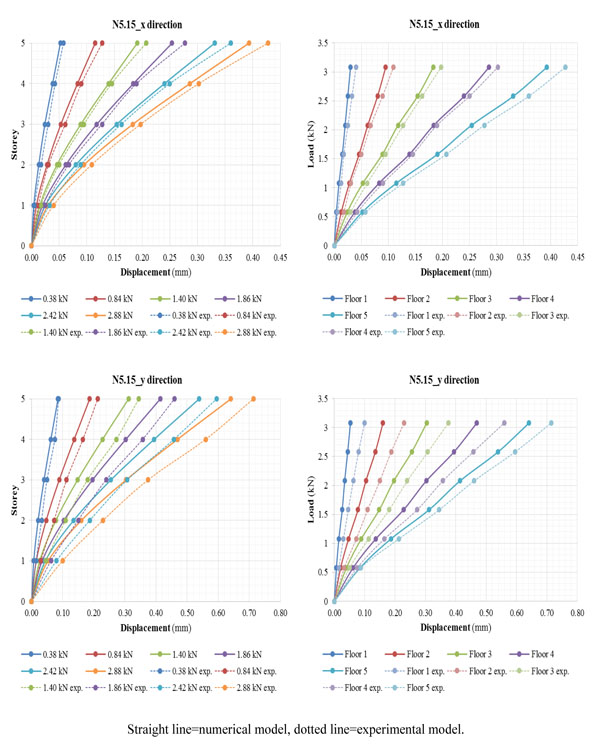
Finally, the results of the linear analysis for the eccentric loading e3 are given and compared with the experimental data in Fig. (11). It may be noted that the eccentric load causes displacements in the X direction mainly higher than those that have been observed in the previous load cases, sometimes even double. In fact, the maximum displacement of the control point N5.15 is equal to approximately 0.400 mm. Similarly, in the Y direction, the maximum displacement is equal to about 0.641 mm.
Referring to the results of the linear analysis in terms of storey/rotation diagrams for the eccentric loading e3 contained in Fig. (12), it can be seen that, also in this case, the eccentric load causes rotations mainly higher than those that have been observed in the previous load cases. Therefore, it is possible to notice that the maximum rotation, obtained by averaging the values of nodes N5.4 and N5.15, is equal to about 0.355 rad*10-3. Instead, at the nodes N5.15 and N5.16, the maximum rotation has a value of 0.321 rad*10-3.
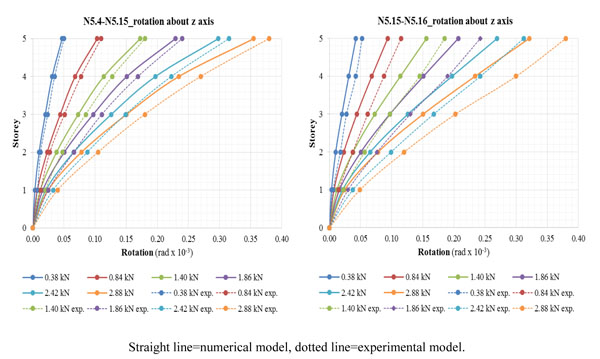
The linear analysis applied to brick masonry structure has proved its ability in predicting the elastic structural behaviour of the experimental tested building, showing numerical results in terms of displacements and rotations in good agreement with the experimental data in all loading conditions. For low values of loading, the linear static analysis can be considered a valid instrument to describe the effects of eccentric shear forces on the response of masonry building, even if it underestimates the actual elastoplastic behaviour of the system.
4.2. Non Linear FE Analysis
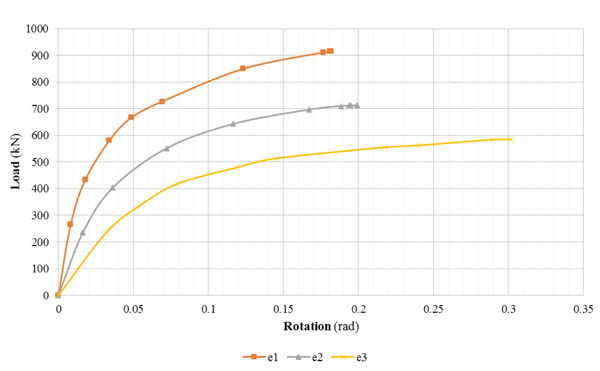
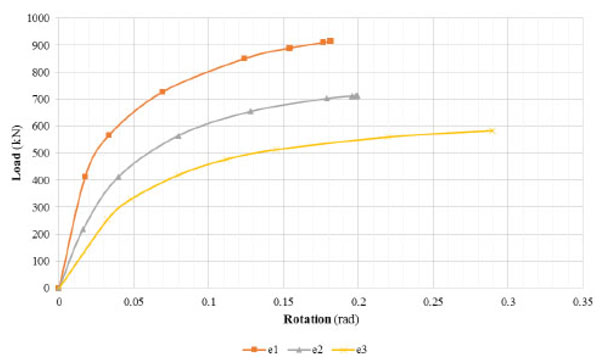
The non linear static FE analysis has been performed to study the behaviour of the 5-storey masonry building in 1/3rd scale and to investigate the ductile capacity of the structural system in relation to the different eccentricities of loading. Removing the hypothesis of a purely linear behaviour, the pushover analysis is helpful to investigate the building response in a wider load range, showing the actual elastoplastic behaviour of the system. Therefore, the building has been able to show displacements and rotations much higher than the experimental case in all control points. Referring to the pushover curves, it can be noted that the structural behaviour is described with a linear-elastic phase much more wide compared to the results of the linear analysis; besides, the plastic phase is characterized by a large ductile range until the collapse of the structure that involves simultaneous the entire building in relation to all load cases. The pushover curve obtained by monitoring the displacements of the control point CM.5 for the symmetric loading is shown in Fig. (13). Horizontal displacements provided by FE linear and non linear models for small values of loads are also compared with the data obtained by experimental tests in Table 10. Considering the standard deviation values, we may note that the theoretical results are confrontable with experimental results. Referring to the eccentric loadings, the capacity curves investigated in each direction have exhibited very similar displacements for small values of loads in agreement with experimental tests (Tables 11-16). From the results shown in Tables 10-16 it is possible to conclude that the comparison between experimental and theoretical data confirms the suitability of FE modelling both in case of linear and non linear analysis for small values of loads.
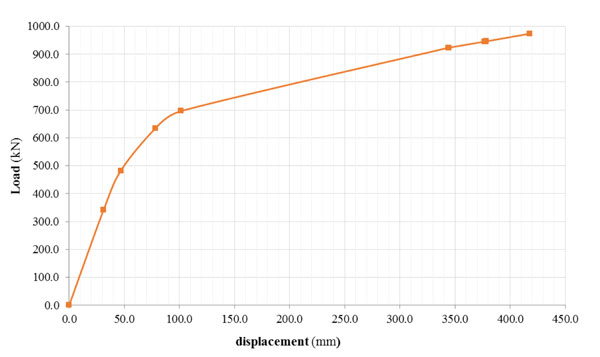
Figs. (14-18) show the pushover curves obtained from different eccentricity of loading by monitoring the displacements and the rotations of the control points N5.4, N5.15 and N5.16. It is possible to notice that the increase of the load’s eccentricity does not affect the elastic limit of the structure. Furthermore the various eccentricities ei with i=0,1,…,3 have mostly influenced the plastic phase of the building for all control points. The failure conditions have been reached for values of displacements that decrease with the increasing of the load’s eccentricity. Referring to the plastic range, as the eccentricity progresses, the steadily increased loads determine different failure displacements of the control points in the X and Y directions and, finally, angles of rotation that gradually increase.
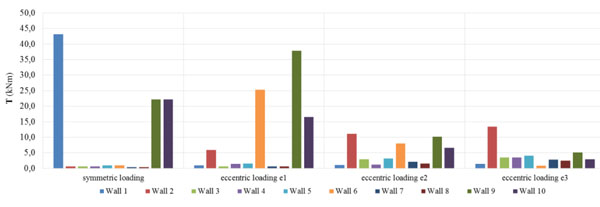
The pushover analysis, carrying the structure beyond the elastic field, is helpful to investigate the maximum values of the flexural strength and shear resistance at which failure occurres. The entity of shear force, V, the bending moment, M, and torsional moment, T, at the ground floor’s walls (Fig. 19) has been evaluated and the comparison of values has been related to different eccentric loadings.
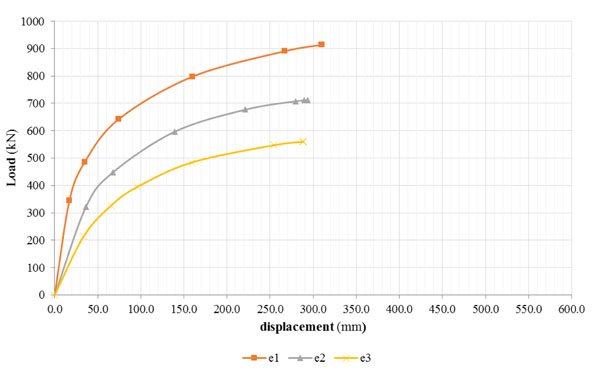
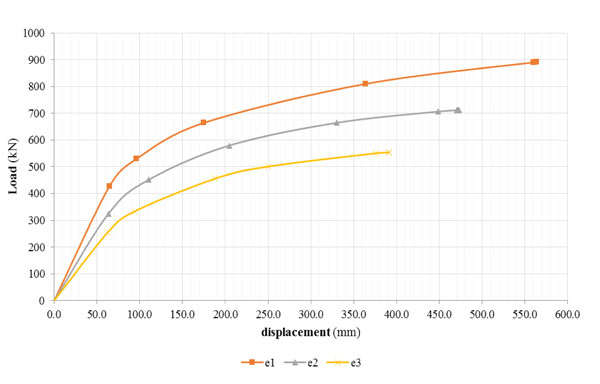
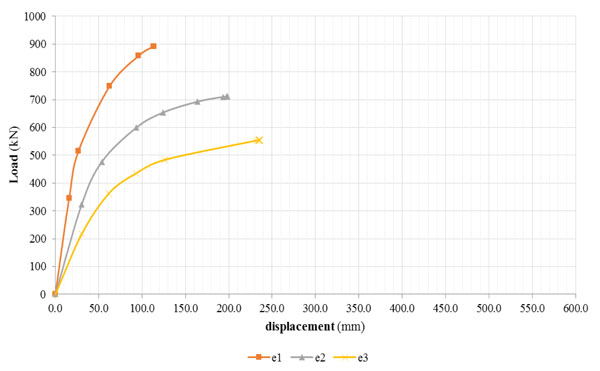
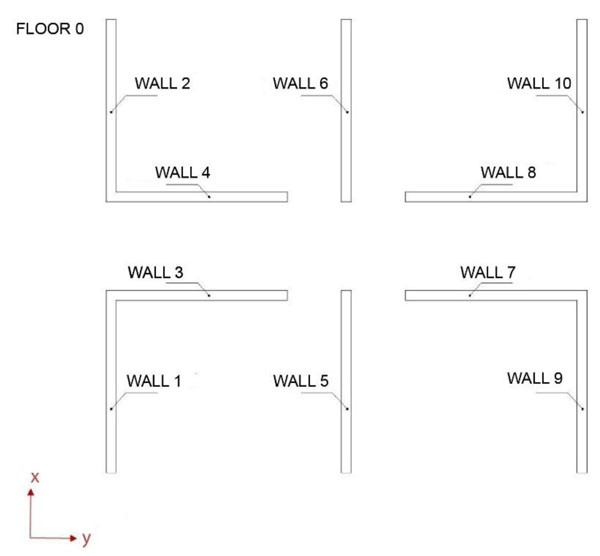
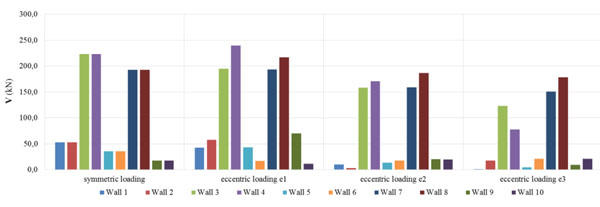
By analysing the shear forces and the bending moments that act on the base of ground floor’s walls, it can be noted that the masonry panels parallel to the direction of the imposed forces are subjected to high forces and moments, much more relevant than the other direction (Figs. 20-21).
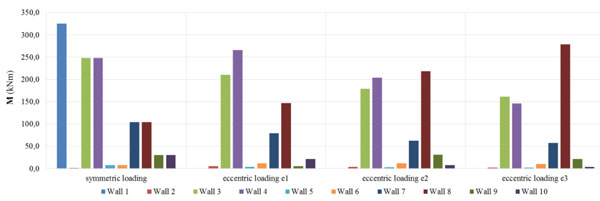
The results of non linear numerical analysis are based on a modelling of deformable elements that influences the structural response. Referring to the masonry walls parallel oriented to the direction of the applied loadings, it can be seen that, by increasing the eccentricity of loadings, shear forces and bending moments decrease, with the exception of the wall No.8 that shows increasing values of bending moment in the different load cases. Instead, the orthogonal walls are characterized by significantly lower shear and bending solicitations, with similar values between them. Moreover, considering the values of the torsional moments, it can be noticed as these have lower intensity in the walls parallel to the direction of the applied loads, while they have higher values in the orthogonal panels. In this case, the torsional moments increase with the decreasing of the shear forces and the bending moments and with the increasing of the eccentricity of loadings (Fig. 22).
| F (kN) | Displacements (mm x 10-2) Point CM5 | ||||
|---|---|---|---|---|---|
| Exp. | FE Linear Analysis |
Standard Deviation Values |
FE Non Linear Analysis |
Standard Deviation Values |
|
| 1.00 | 10.40 | 9.20 | 0.85 | 9.53 | 0.61 |
| 2.00 | 19.50 | 18.40 | 0.78 | 19.06 | 0.31 |
| 3.00 | 29.50 | 27.70 | 1.27 | 28.60 | 0.64 |
| 4.00 | 39.25 | 36.90 | 1.66 | 38.13 | 0.79 |
| 5.00 | 49.50 | 46.10 | 2.40 | 47.66 | 1.30 |
| F (kN) | Displacements (mm x 10-2) Point N5.4 | ||||
|---|---|---|---|---|---|
| Exp. | FE Linear Analysis |
Standard Deviation Values |
FE Non Linear Analysis |
Standard Deviation Values |
|
| 0.75 | 4.00 | 3.30 | 0.49 | 3.72 | 0.20 |
| 1.50 | 8.75 | 6.70 | 1.45 | 7.43 | 0.93 |
| 2.27 | 12.50 | 10.10 | 1.70 | 11.25 | 0.89 |
| 3.03 | 17.75 | 13.50 | 3.01 | 15.01 | 1.94 |
| 3.78 | 22.25 | 16.90 | 3.78 | 18.73 | 2.49 |
| 4.53 | 26.25 | 20.20 | 4.28 | 22.44 | 2.69 |
| F (kN) | Displacements (mm x 10-2) Point N5.15 | ||||
|---|---|---|---|---|---|
| Exp. | FE Linear Analysis |
Standard Deviation Values |
FE Non Linear Analysis |
Standard Deviation Values |
|
| 0.75 | 3.50 | 3.30 | 0.14 | 3.44 | 0.04 |
| 1.50 | 6.75 | 6.70 | 0.04 | 6.88 | 0.09 |
| 2.27 | 10.25 | 10.10 | 0.11 | 10.42 | 0.12 |
| 3.03 | 13.75 | 13.50 | 0.18 | 13.91 | 0.11 |
| 3.78 | 17.50 | 16.90 | 0.42 | 17.35 | 0.11 |
| 4.53 | 20.75 | 20.20 | 0.39 | 20.79 | 0.03 |
| F (kN) | Displacements (mm x 10-2) Point N5.15 | ||||
|---|---|---|---|---|---|
| Exp. | FE Linear Analysis |
Standard Deviation Values |
FE Non Linear Analysis |
Standard Deviation Values |
|
| 0.75 | 10.00 | 10.10 | 0.07 | 11.35 | 0.96 |
| 1.50 | 20.25 | 20.20 | 0.04 | 22.71 | 1.74 |
| 2.27 | 31.40 | 30.50 | 0.64 | 34.37 | 2.10 |
| 3.03 | 42.00 | 40.70 | 0.92 | 45.87 | 2.74 |
| 3.78 | 53.25 | 50.80 | 1.73 | 57.23 | 2.81 |
| 4.53 | 64.00 | 60.90 | 2.19 | 68.58 | 3.24 |
| F (kN) | Displacements (mm x 10-2) Point N5.4 | ||||
|---|---|---|---|---|---|
| Exp. | FE Linear Analysis |
Standard Deviation Values |
FE Non Linear Analysis |
Standard Deviation Values |
|
| 0.58 | 6.75 | 5.20 | 1.10 | 6.54 | 0.15 |
| 1.08 | 13.00 | 9.60 | 2.40 | 12.17 | 0.58 |
| 1.58 | 18.50 | 14.10 | 3.11 | 17.81 | 0.49 |
| 2.08 | 24.50 | 18.60 | 4.17 | 23.44 | 0.75 |
| 2.58 | 30.40 | 23.00 | 5.23 | 29.08 | 0.93 |
| 3.08 | 36.25 | 27.50 | 6.19 | 34.72 | 1.08 |
| F (kN) | Displacements (mm x 10-2) Point N5.15 | ||||
|---|---|---|---|---|---|
| Exp. | FE Linear Analysis |
Standard Deviation Values |
FE Non Linear Analysis |
Standard Deviation Values |
|
| 0.58 | 6.95 | 5.20 | 1.24 | 5.45 | 1.06 |
| 1.08 | 12.75 | 9.60 | 2.23 | 10.15 | 1.84 |
| 1.58 | 17.90 | 14.10 | 2.69 | 14.85 | 2.15 |
| 2.08 | 22.50 | 18.60 | 2.76 | 19.55 | 2.08 |
| 2.58 | 28.50 | 23.00 | 3.89 | 24.25 | 3.00 |
| 3.08 | 33.50 | 27.50 | 4.24 | 28.95 | 3.22 |
| F (kN) | Displacements (mm x 10-2) Point N5.15 | ||||
|---|---|---|---|---|---|
| Exp. | FE Linear Analysis |
Standard Deviation Values |
FE Non Linear Analysis |
Standard Deviation Values |
|
| 0.58 | 11.50 | 10.30 | 0.85 | 11.34 | 0.11 |
| 1.08 | 22.75 | 19.10 | 2.58 | 21.12 | 1.15 |
| 1.58 | 32.75 | 28.00 | 3.36 | 30.90 | 1.31 |
| 2.08 | 42.50 | 36.90 | 3.96 | 40.68 | 1.28 |
| 2.58 | 52.25 | 45.70 | 4.63 | 50.46 | 1.26 |
| 3.08 | 62.75 | 54.60 | 5.76 | 60.24 | 1.77 |
| F (kN) | Displacements (mm x 10-2) Point N5.4 | ||||
|---|---|---|---|---|---|
| Exp. | FE Linear Analysis |
Standard Deviation Values |
FE Non Linear Analysis |
Standard Deviation Values |
|
| 0.38 | 6.75 | 5.30 | 1.03 | 5.95 | 0.56 |
| 0.84 | 15.40 | 11.60 | 2.69 | 13.16 | 1.58 |
| 1.40 | 24.25 | 19.40 | 3.43 | 21.94 | 1.64 |
| 1.86 | 32.50 | 25.80 | 4.74 | 29.14 | 2.37 |
| 2.42 | 42.25 | 33.60 | 6.12 | 37.92 | 3.06 |
| 2.88 | 51.00 | 40.00 | 7.78 | 45.13 | 4.15 |
| F (kN) | Displacements (mm x 10-2) Point N5.15 | ||||
|---|---|---|---|---|---|
| Exp. | FE Linear Analysis |
Standard Deviation Values |
FE Non Linear Analysis |
Standard Deviation Values |
|
| 0.38 | 5.75 | 5.20 | 0.39 | 5.33 | 0.30 |
| 0.84 | 12.75 | 11.50 | 0.88 | 11.78 | 0.69 |
| 1.40 | 20.75 | 19.10 | 1.17 | 19.63 | 0.79 |
| 1.86 | 27.75 | 25.40 | 1.66 | 26.07 | 1.18 |
| 2.42 | 36.00 | 33.10 | 2.05 | 33.92 | 1.47 |
| 2.88 | 42.75 | 39.30 | 2.44 | 40.37 | 1.68 |
| F (kN) | Displacements (mm x 10-2) Point N5.15 | ||||
|---|---|---|---|---|---|
| Exp. | FE Linear Analysis |
Standard Deviation Values |
FE Non Linear Analysis |
Standard Deviation Values |
|
| 0.38 | 8.75 | 8.50 | 0.18 | 9.34 | 0.42 |
| 0.84 | 21.25 | 18.70 | 1.80 | 20.66 | 0.42 |
| 1.40 | 34.50 | 31.20 | 2.33 | 34.43 | 0.05 |
| 1.86 | 46.00 | 41.40 | 3.25 | 45.74 | 0.18 |
| 2.42 | 59.50 | 53.90 | 3.96 | 59.51 | 0.01 |
| 2.88 | 71.40 | 64.10 | 5.16 | 70.82 | 0.41 |
CONCLUSION
The aim of this work is to describe the response under lateral loading of a masonry building model obtained by means of FE modelling and to compare the theoretical results with experimental data.
Main results of this analysis can be generalized to masonry buildings characterized by a symmetric and regular structural disposition and are below summarized.
- The linear static analysis by FE modelling has proven to be capable in capturing the linear elastic behaviour of the tested brick masonry building, showing both lateral displacements and rotations in good agreement with the experimental results in all loading conditions with eccentricity ei with i=0,…,3 being e0=0 and e3=1168 mm.
- The non linear static analysis carried out until theoretical failure, has provided a significant increase in values of displacements and rotations, showing a higher elastic limit than the experimental value of model.
- The elastic behaviour of the structure obtained by linear and non linear analysis for small values of loads is in good agreement with the experimental results.
- The elastic stiffness determined by pushover response is entirely comparable with value from experimental results.
- Eccentric loadings influence the torsional behaviour of the structure causing gradually increasing displacements obviously in the direction orthogonal to applied loading direction. The increase of eccentricity has not affected the elastic limit of the structure, leading to growing torsional effects and different failure modes captured only in the plastic phase.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
This research was supported by research funds provided by Polytechnic University of Marche. The author would like to express their gratitude to the students who collaborated in the development of this research.


