All published articles of this journal are available on ScienceDirect.
Study on Optimization of Landslide Treatment Schemes Based on Entropy Weight Grey Incidence and D-S Evidence Theory
Abstract
Landslide disaster is a serious natural hazard next to earthquake and floodwater. It has brought about great losses to the economic and societal development worldwide. Aiming at the characteristics and requirements in the process of landslide treatment, an optimization algorithm of landslide treatment schemes selection is proposed by combining entropy weight grey incidence with D-S evidence theory. Firstly, it employs the theory to acquire the weights of different indices. Secondly, it determines uncertain degrees corresponding to different indices through the methodology of grey incidence. Finally, the mass functions of different targets in different indices can be obtained, carrying out the fusion of different mass functions on the basis of D-S theory of evidence and sorting the targets according to the belief function value. It is verified by example calculation and comparative analysis that the method is feasible and effective, providing theoretical basis for landslide treatment.
1. INTRODUCTION
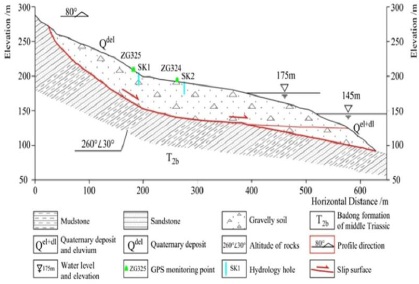
As one of the most important geological disasters, landslide has become a noticeable environment problem for the human society, which results in a large number of casualties and property losses every year. If the occurrence time of landslide can be predicted accurately, the losses it causes can be reduced considerably, as it will be possible to take suitable measures to nip the problem in the bud. For example, The Baijiabao landslide which occurred in Zigui town on the west side of the Xiangxi River was a major tributary to the Yangtze River, 2.5 km from the estuary. The materials of the landslide are quaternary deposits including silty clay and fragmented rubble with a loose and disorderly structure. The lithologies of the bedrock and strata that crop out around the landslide are mainly Jurassic arkosics, silty mudstones and muddy siltstones, with dip directions ranging from 260° to 285° and dip angles from 30° to 40° (Fig. 1). According to the observations of surface cracks in the Baijiabao landslide made from 2007 to 2012, the macroscopic deformation develops are shown in Fig. (2). In June 2007, surface cracks first appeared at the road on the right side of the landslide. After July in the same year, an arc tension-crack occurred with a total length of about 160 m. Apparently, it became the upper boundary of the landslide. Meanwhile, the tension cracks in the middle of the road grew more evident, and the road surface became seriously broken. Besides, in July 2012, some cracks were still extending backward, and the actuate cracks on the back part of landslide were inclined to link up, which showed that the Baijiabao landslide was apparently deforming in its entirety. Aiming at the complexity and the uncertainty of optimal selection of landslide treatment scheme, it is important to systematically study the way of control of the landslides to provide scientific basis for engineering practice, however, available schemes suggest that engineering measures can control the independent landslides that together constitute the huge landslide mass, in turn avoiding the need for costly relocation of thousands of people.

At present, the research of the landslide treatment project in terms of technical level has made great progress, however, the research of the scheme evaluation and optimal selection is relatively rare. With regard to the aspect of treatment scheme, some optimization methods have been put forward successively, such as comprehensive scoring method, entropy weight decision method and case analysis method [1-11]. These methods have their own advantages and disadvantages, which are also greatly influenced by subjectivity. Therefore, the methods can reduce the effect of subjectivity through the expert comprehensive scoring. In addition, the evaluation objects are considered as being passive by some evaluation methods, which have no voice in the evaluation process certainly. Therefore, the traditional evaluation methods cannot already be promising at an optimum level, seeking control of the dependability of the schemes; therefore, there is a need to explore a new kind of appraisal method.
The Dempster-Shafer theory of evidence, also called D-S theory, was presented by Dempster and developed by Shafer [12, 13]. The theory was firstly proposed by Dempster in 1967, and then developed to its present form by his student Glenn Shafer in 1976. Evidence theory can present and handle uncertainty with better performance than probability theory [12-14]. D-S evidence theory provides an efficient synthesis rule for the uncertain information, moreover, the data fusion consists in obtaining a single belief function by the combination of several belief functions resulting form distinct information sources [15, 16]. Dempster’s combination rule is the most crucial instrument of D-S theory and it possesses several interesting mathematical properties, such as commutative and associative [17]. Nowadays, the evidence theory has been widely used in the Multiple-Objective-Comprehensive-Evaluation research of uncertainty problems, such as target recognition [18], decision making [19-22], reliability analysis [23-26] and so on.
As one of the analysis methods of grey system theory, grey relational analysis is used to determine the relational degree of the factors according to the similarity degree of the geometry of the various factors changing curve. And grey relational analysis is also applicable to the irregular data. Furthermore, by using grey relational analysis, there does not appear inconsistency between the quantitative results and the qualitative analysis [27]. The application of grey relational analysis in sequence decision-making on the development and utilization of mineral resources can play all the advantages of its own. Based on this point, a new comprehensive method for evaluating the optimization of landslide treatment scheme is proposed so as to deal with the uncertainty of information and subjective preference in the decision process with a better way.
2. THE BASIC PRINCIPLE OF ENTROPY WEIGHT GREY INCIDENCE METHOD
2.1. Determine the Index Weight [28-31]
Aiming at the complexity and the uncertainty of optimal selection for landslide treatment scheme, combined with the corresponding survey data parameters, the membership grade gij of scheme i can be calculated under the index j which makes the membership matrix of scheme G = (gij)m×n.
The weights for evaluation factors in the model were obtained from the value of data reflecting information entropy. For the evaluation object of multi-attribute decision making, the weighting methods are as follows.
Meanwhile, the membership matrix of scheme G = (gij)m×n can be normalized by the formula.
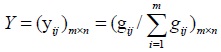 |
(1) |
The entropy value of index j can be expressed as follows.
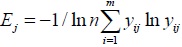 |
(2) |
Thus, the weight of index j is proposed as
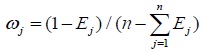 |
(3) |
Where
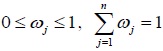 . Moreover, the weighted membership degree matrix can be determined by (yij)m×n
. Moreover, the weighted membership degree matrix can be determined by (yij)m×n
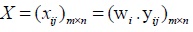 |
(4) |
2.2. Structure of the Mass Function
As an important data fusion method, Dempster-Shafer(D-S) evidence theory [12, 13] can effectively solve the uncertainty problem in Multiple-Objective-Comprehensive-Evaluation research. Mass function fusion is the basis and assurance of multi-information integration. Therefore, the key step for solving uncertainty reliability of each index becomes particularly important. In this paper, the uncertainty reliability of each index can be obtained by grey correlation analysis method.
The qth-order uncertainty reliability of index j can be set as follows.
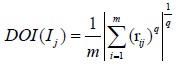 |
(5) |
In the formula, q = 2, rij is the comprehensive grey correlation coefficient of (xij)m×n. Its solution process is as follows; firstly, the optimal correlation coefficient rij+ and worst correlation coefficient rij- can be expressed as follows respectively.
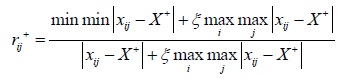 |
(6) |
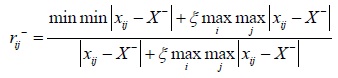 |
(7) |
Where
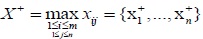 is ideal optimal sequence,
is ideal optimal sequence,
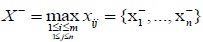 is ideal worst sequence, ξ = 0.5, thus the comprehensive grey correlation coefficient was calculated by using the following equation.
is ideal worst sequence, ξ = 0.5, thus the comprehensive grey correlation coefficient was calculated by using the following equation.
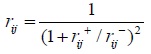 |
(8) |
Then putting rij into formula (5), the qth-order uncertainty reliability DOI(Ij) of indexcan be calculated by it; finally, the Mass function mj(i) of each index can also be determined by
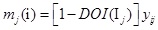 |
(9) |
Where
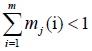 , then Mass function mj(i) of each index is given in the framework of identification Θ, that is, it can reflect the degree of support for all schemes, therefore, the overall uncertainty Mass function of index j can be obtained by the following equation.
, then Mass function mj(i) of each index is given in the framework of identification Θ, that is, it can reflect the degree of support for all schemes, therefore, the overall uncertainty Mass function of index j can be obtained by the following equation.
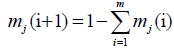 |
(10) |
3. THE SYNTHESIS OF MASS FUNCTION BY D-S EVIDENCE THEORY
The D-S evidence theory is a decision-making method used to solve uncertain and risk decision-making problems. It describes the accuracy of the proposition by introducing a confidence measure, which can also deal with the uncertainty caused by “ignorance” of propositions. Therefore, the Mass function obtained above is synthesized by using D-S theory of evidence, in order to improve the accuracy of decision-making and reduce the uncertainty.
3.1. D-S evidence Theory [32-38]
The D-S evidence theory is a kind of information fusion technology, which uses the D-S synthetic rules to fuse the reliability of different evidence bodies. It is called “recognition framework” based on the reliability of synthetic resulting from fusion sample space, and it is expressed by Θ, which is made up of some mutually exclusive proposition complete sets. Assuming that basic probability assignment m to proposition A :2Θ → [0,1] and following two conditions should be met:
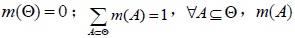 is the probability distributive function of Θ. For the proposition A, defined function Bel 2Θ → [0,1] is the belief function of Θ.
is the probability distributive function of Θ. For the proposition A, defined function Bel 2Θ → [0,1] is the belief function of Θ.
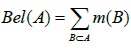 |
(11) |
Where, the belief function Bel(A) represents the minimum value of total trust that supports A. For two independent Mass functions m1 and m2 defined in the same identification framework, the synthetic formula is as follows.
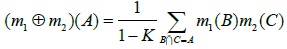 |
(12) |
In the formula,
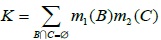 , and K ≠ 1.
, and K ≠ 1.
3.2. The Synthesis of Mass Function
The above theory foundation, D-S Evidence theory is applied to synthetic the Mass function of different schemes, therefore, the multiple function synthesis can be expressed as
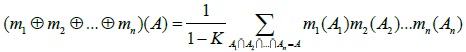 |
(13) |
Where,
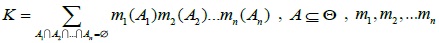 is a Mass function of the framework of identification Θ.
is a Mass function of the framework of identification Θ.
3.3. Algorithm Process
To summarize, we can find that the algorithm process of landslide treatment based on entropy weight grey incidence and D-S Evidence Theory which can be expressed as follows.
Step 1: Entropy theory is used to calculate the weight of each index ωj(j = 1,2,......,n), and the weighted membership degree matrix (xij)m×n can be obtained.
Step 2: Through calculating the comprehensive grey correlation coefficient rij of weighted membership degree matrix (xij)m×n, and the qth-order uncertainty reliability DOI(Ij) of index j can be determined by the formula (5).
Step 3: According to the formula (9) and formula (10), the Mass function mj(i) and overall uncertainty Mass function mj(i + 1) of index j also can be obtained, respectively.
Step 4: Then, the Mass function of each scheme is fused by D-S Evidence theory to form the final result.
Step 5: According to the size of the synthesized confidence function, excellent and inferior orders between schemes and feasibility of each scheme are obtained at the same time in this paper.
4. ENGINEERING PRACTICE ANALYSIS
In order to verify the effectiveness of the suggested model, this thesis researches on the stability of landslide, and takes schematic geological cross-section of Baijiabao landslide as an example on the basis of the detailed investigation of the geological disorders. The landslide occurred in Zigui town on the west side of the Xiangxi River, a major tributary of the Yangtze River, 2.5 km from the estuary. According to the landslide's geographical location, soil conditions, hydrological and meteorological conditions, and fully taking its specificity of disaster control in the scenic spot, have put forward three kinds of protection schemes for landscaping and ecological protection [5-7].
SchemeA1: Landscape type anti-slide pile + intercepting drain and drainage ditch
SchemeA2: Landscape retaining wall + fiber bundle seepage-guiding drainage hole + intercepting drain and drainage ditch
SchemeA3: Lattice slope protection + bamboo living water + intercepting drain and drainage ditch
SchemeA4: Surface-drainage + Load reducing foot + monitoring and warning
SchemeA5: Local clearing + cantilever anti slide column +surface-drainage
SchemeA6: Lattice ditch slope protection + underground-drainage + cantilever anti slide column
SchemeA7: Anchor cable anti-slide pile + cantilever anti slide column + surface-drainage
SchemeA8: Cantilever anti-slide pile + cantilever anti slide column + surface-drainage
SchemeA9: Surface-drainage + local clearing + intercepting drain and drainage ditch
SchemeA10: Fiber bundle seepage-guiding drainage hole + cantilever anti slide column + drainage
The application of this program indicated that it worked well in deciding the project of landslide control. In order to carry on the reasonable evaluation of landslide treatment in engineering, several factors have been selected as evaluation index such as the landscaping, safety reliability, reasonable economy, and technical feasibility. The optimal model of landslide treatment schemes is shown in Fig. (3), and the pretreatment data of three landslide treatment schemes are shown in Table 1.
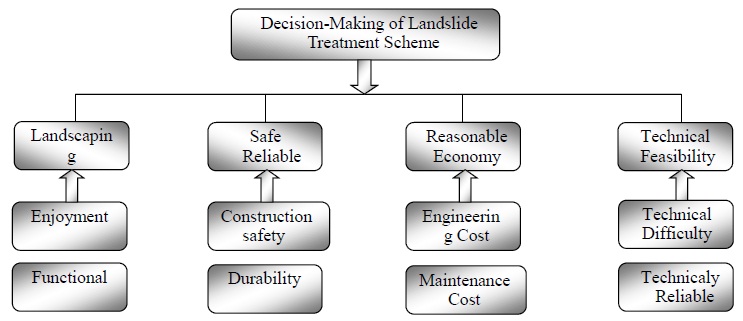
| Scheme | Landscaping | Safe Reliable | Reasonable Economy | Technical Feasibility |
|---|---|---|---|---|
| A1 | 0.798 | 0.883 | 0.883 | 0.961 |
| A2 | 0.973 | 0.594 | 1.000 | 0.368 |
| A3 | 1.000 | 0.937 | 0.726 | 1.000 |
| A4 | 0.753 | 0.270 | 0.487 | 0.852 |
| A5 | 0.876 | 0.006 | 0.135 | 0.298 |
| A6 | 0.918 | 0.390 | 0.607 | 0.698 |
| A7 | 0.593 | 0.631 | 0.198 | 0.809 |
| A8 | 0.777 | 0.278 | 0.325 | 0.527 |
| A9 | 0.950 | 0.703 | 0.110 | 1.000 |
| A10 | 0.970 | 0.835 | 1.000 | 0.056 |
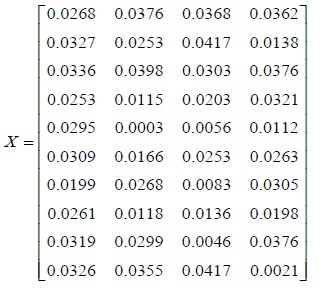
The weight of each index is ω = (0.2894, 0.2350, 0.2283, 0.2473)
And the weighted membership degree matrix (xij)m×n can be obtained as,
 |
The ideal optimal sequence and ideal worst sequence will be determined.
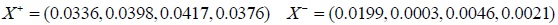 |
Next, the maximum difference and minimum difference are calculated below, respectively.
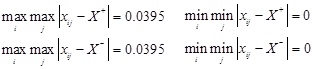 |
Thus, the comprehensive grey correlation coefficient rij of weighted membership degree matrix is,
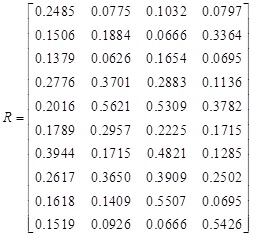 |
The qth-order uncertainty reliability DOI(Ij) of index and Mass function of each scheme can be calculated as follows, respectively.
DOI(I1) = 0.0726, DOI(I2) = 0.0881, DOI(I3) = 0.1072, DOI(I4) = 0.0830
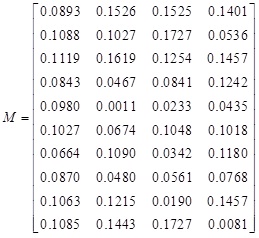 |
Therefore, the overall uncertainty Mass function of index j can be obtained by the formula (10)
m1(11) = 0.0369, m2(11) = 0.0449, m3(11) = 0.0551, m4(11) = 0.0424
Finally, setting the recognition framework as Θ = {A1,A2,.....A10}, and 2Θ = { {A1},{A2},.....{A10} }, according to the D-S Evidence theory, the credibility function of each subset can be synthesized as follows.
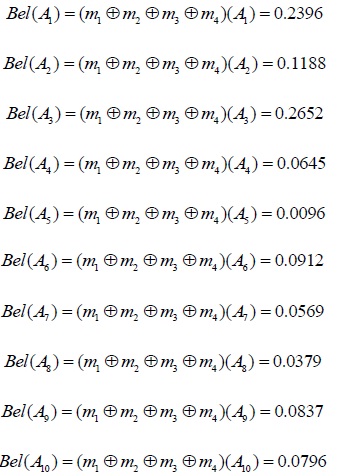 |
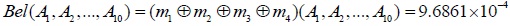 |
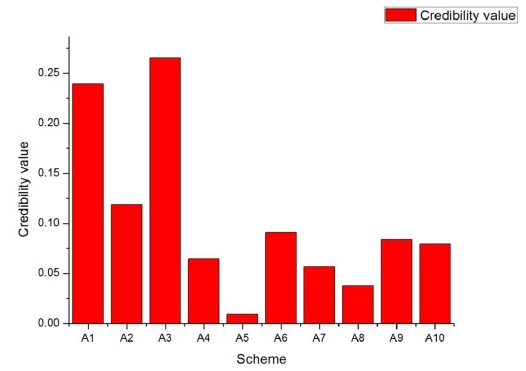
By means of analysis of the calculating result and credibility function, the optimum selection order of landslide treatment schemes is taken as follows, A3 > A1 > A2 > A6 > A9 > A10 > A4 > A7 > A8 > A5, as shown in Fig. (4). Therefore, the optimal scheme is Landscape retaining wall + fiber bundle seepage-guiding drainage hole + intercepting drain and drainage ditch, and the characteristics of four factors are fully considered. On the basis of the above decision-making model, this paper focuses on the Bel(A1,A2,.....A10) value which has gradually decreased to a preset value in the fusion process, which shows that the combination of grey correlation and evidence theory can effectively deal with multi-source uncertain information. So it can reduce the uncertainty and improve the reliability of the information. And the entropy theory is used to determine the index weight to make the decision-making process more objective simultaneously.
CONCLUSION
At present, landslide-block project and interaction of the slippery body have become one of the hot issues being relevant to scientific and technical personnel study in the field of engineering. How to design an optimum landslide treatment plan economically and safely has practical value to national economy construction and development. In this study, the paper has taken the landscaping, safety reliability, reasonable economy and technical feasibility as evaluation factors according to the complexity and the uncertainty of optimal selection of landslide treatment scheme; in addition, an optimization algorithm of landslide treatment schemes selection is proposed by combining entropy weight grey incidence with D-S evidence theory, which has a good applicability for the multiple criteria decision making problem. Furthermore, the suggested method can also reduce the uncertainty in the process of information fusion. The decision of the landslide control scheme is a very complicated system engineering problem, which has a number of issues that need to be explored in depth for this kind of study.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
This work is supported by the National Twelfth Five-year Technology Support Projects of China (Grant No.2015BAK14B01) and PICC Disaster Research Funded Project (Grant No. 2013D32). The authors thank the anonymous reviewers for their constructive comments.


