All published articles of this journal are available on ScienceDirect.
Improved Artificial Bee Algorithm for Reliability-based Optimization of Truss Structures
Abstract
Introduction:
In order to optimize the reliability of the truss structure more effectively, an improved artificial bee colony algorithm based on small interval was proposed and employed to the engineering practice.
Method:
First, the optimization model based on the reliability was set up. In the model, the bars were treated as design variables, and the total weight was the object function. Then, the comparisons with other methods in solving the truss structure discrete variable optimization demonstrate the feasibility and effectiveness of the improved algorithm.
Conclusion:
This work provides a new method for the reliability-based optimization of truss structures.
1. INTRODUCTION
The truss structure is a structure which has been used widely. Optimization design of truss structure is a method for reducing the project cost and guaranteeing the quality under the requirements of the structural safety. With the increasing complexity of the structure, the traditional optimization methods cannot optimize effectively the reliability-based optimization design of the truss structure [1]. It is urgent for us to find more effective methods to optimize the truss structure. In recent years, with the development of computer technology, more and more swarm intelligence optimization algorithms were used to truss structure optimization [2-6]. All these works have promoted the development of the structure optimization. But, we still have a long way to go, especially, how to overcome the premature of the algorithms. According to this, a novel algorithm, the improved artificial bee colony algorithm was proposed and employed to the truss structure optimization.
The artificial bee colony algorithm (ABC algorithm) was first proposed by Turkish, Karaboga in 2005 [7]. The algorithm simulates the process of food searching of honeybee populations by imitating the population exchange mechanism. The ABC algorithm has strong global search ability with less control parameters. Since proposed, the algorithm has been used for solving many combinatorial optimization problems successfully [8-15]. But the ABC algorithm also has shortcomings such as being premature. Many scholars have done a lot to overcome the disadvantage of the algorithm. Babaeizadeh S. proposed constrained artificial bee colony algorithm where three new searching strategies were introduced to the employed bee, onlooker bee and scout bee respectively. The numerical results demonstrated the efficiency of the improved algorithm [16]. Aydoğdu İ. proposed an enhanced artificial bee colony algorithm and employed it to optimize the steel space frames design [17]. Hashim H. A. proposed an enhanced deployment algorithm based on ABC algorithm [18]. Oshaba A. S. proposed a novel ABC algorithm to optimize parameters of maximum power point tracking and speed controller [19]. Alshamiri A. K. proposed an improvement method to solve the extreme learning machine projection [20]. Harfouchi F. developed cooperative learning ABC algorithm [21], and so on. These works have promoted the development of the ABC algorithm. But, the problem of the premature solving still has a long way to go.
To overcome prematurity of the algorithms, an improved strategy with the small interval was proposed and the improved algorithm was introduced to the truss structure optimization.
The rest of the paper was organized as follows. First, the basic knowledge of the ABC algorithm was introduced and the improved algorithm was proposed. Then, it was employed to the truss structure optimization after the establishment of the optimization model. Finally, the efficiency of the algorithm was shown by comparison with other algorithms.
2. IMPROVED ARTIFICIAL BEE COLONY ALGORITHM
2.1. Basic Principle of ABC Algorithm
As a kind of new algorithm derived from the foraging behavior of bee populations, the ABC algorithm solves the multidimensional and multimodal optimization problems successfully by simulating the behaviors of the real bees. In the algorithm, the bee colony was divided into tripartite: employed bees, onlookers and scouts. The employed bees visit the food source firstly, the onlookers decide which food source should be visited in dancing area, and the scouts are random search bees.
In the initialization phase, food source locations were randomly selected and their amount of nectar was a constant. Employed bees showed the information of food source. In the second phase, each employed bee recorded the food source visited previously, and then chose a new source in the neighborhood. In the third phase, each onlooker chose food source based on the information shown by the employed bees. The more nectar the route had, the easier it was selected. In artificial bee colony algorithm, the food source locations represented the possible solutions and the amount of nectar was the fitness of the solution. In the ABC algorithm, SN denoted the size of the initial population. Each solution is a D-dimensional vector. The employed bees searched for the new solution and tested its fitness. The new solution was generated as follow:
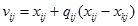 |
(1) |
Where, vij was the new solution, xij was the known solution, qij was a factor whose value is [-1, 1], xkj was a solution in the neighborhood.
If the new solution is better than the previous one, the previous solution was replaced. After completing the search process, the next onlookers were chosen by using Eq. (2).
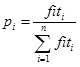 |
(2) |
Where, pi was the probability of selection, fiti was the fitness value
In artificial bee colony algorithm, the solution without improvement will be abandoned after the limited cycle times.
2.2. Improved Strategies of ABC Algorithm
The ABC algorithm received extensive attention of scholars all over the world since it was proposed. It has many advantages, such as simple calculation and higher robustness. So, it was easy to be used to deal with the combinatorial optimization problems. But the defects of algorithm were exposed gradually after several years’ research, such as lower convergence speed, lower calculation accuracy and the premature.
Here, a novel improved artificial colony based on small interval search algorithm was proposed. The parameter l was introduced into the process of initialization to make the initial solution distributed throughout the search domain as much as possible. This strategy can improve the global and local search ability of the algorithm. At the same time, the tabu search and sets parameter γ were introduced to eliminate the local optimal solution.
The main improvement of the algorithm was as follows.
First, in the basic ABC algorithm, the initial solution was generated randomly, which influenced the quality of the region search. In order to overcome the defect, the parameter l was introduced into the Eq. (1) .
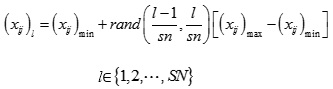 |
(3) |
This improvement ensured that the initial solution can be evenly distributed in the whole range. In the process of data processing, the original solution was replaced. The new solution was as follows.
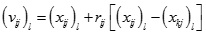 |
(4) |
Where, k ϵ {1,2,…, SN}, K ≠ i, k was in the neighborhood of.
At the same time, the tabu search was employed as a penalty parameter γ was used to compare with the new solutions. If the fitness of new solution is better than γ, it will be replaced. Otherwise, it will not be replaced. This process was repeated until the better fitness was found.
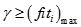 |
(5) |
Where, was the maximum fitness of every iterative.
2.3. Efficiency of Improved ABC Algorithm
In order to verity the effectiveness of the improved algorithm, three standard test functions and the TSP (Travelling Salesman Problem) problems were selected. And the results were compared with other algorithms.
The function of Sphere, Rosenbrock, and Rastrigin were defined as follows:
(1) Sphere function
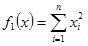 |
(6) |
The value of x was [-5.12, 5.12].
(2) Rosenbrock function
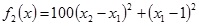 |
(7) |
The value of x was [-2.048, 2.048]
(3) Rastrigin function
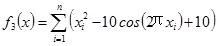 |
(8) |
The value range of x was [-5.12, 5.12]
The dimension of the above functions was 30. The basic control parameters of artificial bee colony algorithm were: SN = 100, MCN = 300, limit = 50. The results obtained after 30 times were shown in Table 1.
| Function | Results | |
|---|---|---|
| Improved ABC algorithm proposed here | Basic ABC algorithm | |
| Sphere | 3.11E-14 | 6.92E-14 |
| Rosenbrock | 4.72E-03 | 8.46E-03 |
| Rastrigin | 7.19E-13 | 4.97E-12 |
As shown in the Table 1, the optimization results of the improved ABC on the test function were better than the basic ABC.
To verify the performance of the improved algorithm, the TSP problem was used too. And the TSP-Chn 31 was selected.
TSP-Chn 31—International standard test of TSP problem with 31 cities.
The basic parameters of the algorithms were shown in the Table 2.
| Ant colony algorithm | Basic ABC algorithm | Improved ABC algorithm proposed here | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Α | β | ρ | Q | α | β | maximum iteration | limit | α | β | Maximum iteration |
limit |
| 1 | 2 | 0.1 | 1 | 1 | 5 | 200 | 10 | 1 | 5 | 200 | 10 |
The result were shown in Table 3 and Fig. (1).
| Comparative items | Best optimal solution | Improved ABC proposed here | Basic ACO | Basic ABC | Other improved ABC algorithms |
|---|---|---|---|---|---|
| Optimum solution | 15381 | 15374 | 15404 | 15736 | 15737 |
| iterations | - | 48 | 169 | 81 | 50 |
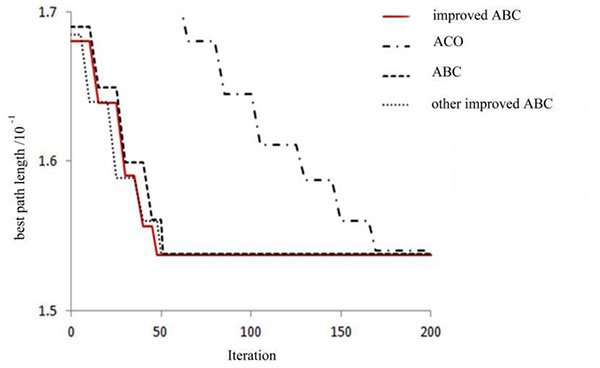
From the above result, we can observe that on the problem of TSP Chn 31, the improved artificial bee colony algorithm proposed here can achieve the optimal solution 15374 at the 48th generation, and the final result was the best among the results obtained by using ant colony algorithm, the basic artificial bee colony algorithm and the other improved methods of artificial colony algorithm. Therefore, compared with the basic ant colony algorithm, basic artificial bee colony algorithm and other improved artificial bee colony algorithm, the improved algorithm we proposed has the better searching capability.
Then, we will introduce it to the truss structure optimization as shown in Fig. (2).
3. TRUSS STRUCTURE OPTIMIZATION
3.1. Mathematical Model of Truss Structure Optimization
- Design variable: Ai was the bar sectional area.
- Object function: The total weight of bar was the object function [22]
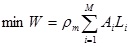 |
(9) |
Where, W was the total weight of bar; ρm was material density; Ai was the sectional area of bar i ;Li was the length of bar i.
- Constraint condition
- a) The stress constraint: σi ≤ [σi].
- b) The displacement constraint: µj ≤ [µj].
- c) The upper and lower bounds of design variables: Ai ϵ {S}.
- [σi],σi—the allowable stress and the most unfavorable stress of bar.
- [µi],µi—the allowable displacement value and displacement value of specific nodes given direction.
- {S}—the sets of bar section size variable.
- d) Reliability constraints
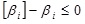 |
(10) |
βi was the reliability index, [βi] was the allowable reliability indicator value, here the [βi] was 3.4. Each bar of truss structure under the node load was axial stress. The relationship between reliability index and sectional area was as follow [23]:
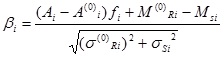 |
(11) |
Where, Ai(0) was the initial sectional area. MRi(0), σRi(0) were the mean and standard deviation of sectional area of bar i respectively. MSi, σSi were the mean and standard deviation of load effect of bar i respectively.
3.3. Examples
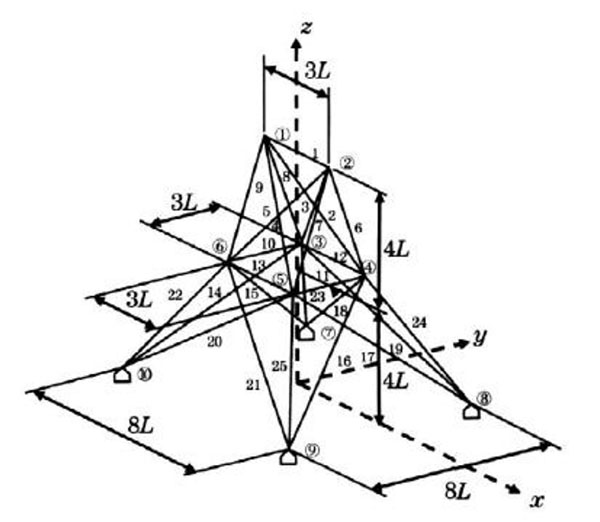
To compare the results more clearly, we employed the example of the references [24, 25]. It was a 25-barspatial truss structure model shown in Fig. (3). The basic parameters of the improved artificial bee colony algorithm were: population size was 25, the maximum number of iteration was 200, and the limit was 10. The basic parameters of truss structure were shown in Tables 4-6.
| Bar length |
Elasticity modulus |
Material density |
Stress constraint |
The maximum vertical displacement of node1and 2 |
|---|---|---|---|---|
| 0.635m | 6.895×104MPa | 2.678×103kg/m3 | [-275.8,275.8] | 8.889mm |
| Node number | Fx | Fy | Fz |
|---|---|---|---|
| 1 | 4.448 | 44.482 | -22.241 |
| 2 | 0 | 44.482 | -22.241 |
| 3 | 22.241 | 0 | 0 |
| 6 | 22.241 | 0 | 0 |
| Group number | Bar number |
|---|---|
| 1 | A1 |
| 2 | A2~A5 |
| 3 | A6~A9 |
| 4 | A10~A11 |
| 5 | A12~A13 |
| 6 | A14~A17 |
| 7 | A18~A21 |
| 8 | A22~A25 |
It has been observed that the stress constraint in compression was different from the stress constraint in tension. The stress constraint in compression should not only meet the strength conditions, but also meet the stability conditions. In the optimization process, the stable critical stress had been set, the buckling of the structure will not occur. So, the buckling of the structure will not be considered here.
The truss optimization results obtained from the improved ABC algorithm were shown in Table 7 (And the results of improved GA and PSO algorithms can be seen from [26] and [27] respectively) and the iterative curve was shown in Fig. (4).
| Group number | Bar sectional area (mm2) |
|---|---|
| Improved ABC | |
| 1 | 64.9 |
| 2 | 234.5 |
| 3 | 2230.1 |
| 4 | 63.149 |
| 5 | 1226.1 |
| 6 | 501.7 |
| 7 | 89.5 |
| 8 | 2568.3 |
| Weight (kg) | 214.702 |
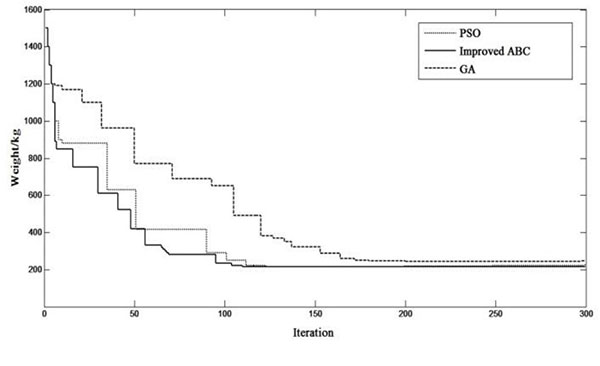
Under the same constraints, the 25-bar truss structure was optimized by three algorithms. The GA algorithm finds its optimal solution at the iteration 170 times. The PSO algorithm finds the optimal solution when the algorithm iteration was 120 times. The improved ABC algorithm we proposed finds the optimal solution in the iteration at 100 times. From Table 7 and Fig. (4), we can know that by using the improved artificial bee colony algorithm we proposed, the structure weight was 214.702kg. It is better than the results obtained from the genetic algorithm and the particle swarm optimization algorithm. Comparing with the genetic algorithm and the particle swarm optimization algorithm, the improved algorithm proposed here has higher convergence speed and convergence precision.
CONCLUSION
Truss structure optimization has significance in theory and practice. The characteristics of discrete variable optimization determine the special requirements on the optimization methods. The traditional methods have some defects. To find a more effective method for this question, an improved artificial bee colony algorithm based on small interval search was proposed. Engineering practice and comparison with other algorithms show that the improved algorithm can enhance the local search ability and it has higher convergence precision. Then, it was introduced to the truss structure optimization, the results show that it can reduce the numbers of structure analysis and solve the truss structure optimization more effectively. The study provides a novel method for the structure optimization.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
The work was supported by Program of Selection and Cultivating of Disciplinary Talents of Colleges and Universities in Hebei Province (BR2-206) and the Natural Science Foundation of Hebei Province, China (No. E2012402030) .


