Cold Rolling Effects on Material Properties in Pallet Rack Uprights

All published articles of this journal are available on ScienceDirect.

RESEARCH ARTICLE

Cold Rolling Effects on Material Properties in Pallet Rack Uprights

Andrei Crisan Adrian Ioan Dogariu, * Open Modal
Authors Info & Affiliations
The Open Civil Engineering Journal • 30 Jun 2017 • RESEARCH ARTICLE • DOI: 10.2174/1874149501711010319

Abstract

Pallet rack structures are usually made up of thin walled cold formed steel sections. The cold rolling process changes the material properties, increasing the yield strength and tensile strength across the section. According to EN1993-1-3, an equivalent yielding strength is allowed to be considered in design to account for the changes in material properties. It has to be mentioned that this approach does not take into account the residual stresses that arise following the forming process. The current paper presents the experimental evidence of residual stresses as result cold rolling process for two pallet rack upright sections. Based on experimental findings, a series of numerical models were created in order investigate the influence of residual stresses onto the load bearing capacity of pallet rack uprights. The experimental program was developed within the CEMSIG Research Centre (http://cemsig.ct.upt.ro) of “Politehnica” University of Timisoara. The increase of yield strength and tensile strength across the cross-section was also experimentally determined.

Keywords: Pallet rack upright, Cold-forming, Yield strength, Tensile strength, Residual stress.

1. INTRODUCTION

Cold-rolled sections represent the most widely used structural steel product for pallet rack upright sections. Despite their lightness, pallet rack systems are able to carry very high loads and can also raise to considerable height. Usually, upright members are made of mono-symmetrical sections, subjected to axial compression and bending about both axes. Even if in the last years numerous investigations were devoted to investigate the effects of holes and member slenderness on the ultimate capacity of pallet rack uprights, various forms of simple and/or coupled instabilities, little or no attention was paid to the effects of the cold rolling process itself.

Material properties play an important role in the performance of thin walled structural members. It is important to be familiar with the mechanical properties of the steel sheets used in cold-formed steel construction before designing this type of steel structural members. Following the cold rolling process, the material properties becomes uneven over the cross-section. The corners area is more affected by plastic deformations and consequently hardening, hence, the changes in material properties are more pronounced in corner areas than for flat areas. In practical design, this increase may be accounted by using an average yield strength across the section, fya defined in EN1993-1-3.

In past years, several studies regarding the material imperfections and their influence on steel elements were conducted. Hu [1] investigated the capacity of thick-wall cold formed steel with square and rectangular hollow cross-sections considering the strain hardening due to forming process. Experiments were carried out to determine the mechanical properties of the flat coupons, corner coupons, parent steel coupons and full section stub columns. It was shown that the strength predicted by the Australian/New Zealand standard using material properties and that forecasted by the Chinese standard based on the average design yield stress of the full section are a little conservative. Also, the two mean strengths predicted by Australian/New Zealand standard based on the mean design yield stress and forecasted by the Chinese standard using material properties determined by tests were found to be identical. Yaghi [2] used FE simulations, validated by experimental measurements, to predict the residual stresses that arise following the welding process. The FE simulations of the welding were comprised of thermal and sequentially coupled structural analyses. The thermal analyses modelled the heat evolution produced by the welding arc, determining the temperature history throughout the FE models. Following structural analyses used the computed temperature history as input data to predict the residual stress fields throughout the models. It was shown that before post-weld heat treatment (PWHT), at certain locations in the weld region and heat affected zone (HAZ) in the pipes, tensile hoop and axial residual stresses approach the tensile strength of the material, presenting a high risk of failure. It has also been found that PWHT substantially reduces the magnitude of residual stresses by varying degrees, depending on the material. Ban [3] conducted an experimental study in order to quantify the residual stresses in 420 MPa high-strength steel hot-rolled equal angle sections. To quantify the residual stresses, the experimental study was conducted by using the sectioning method. The residual stress magnitude and distribution was obtained for 15 sections, and the effect of the width-thickness ratio was also clarified. Based on the test results, it was found that the ratio between the residual stress and the steel yield strength for 420 MPa steel angles with equal legs was much smaller than that of normal strength steel angles; however, the distribution was found to be similar. The residual stress magnitudes was found to be significantly correlated with the width-thickness ratios of the legs. In addition, calculation formulas for the residual stress magnitudes were proposed in which the width-thickness ratios of the angle legs were taken into account. Furthermore, three distribution models were established to be incorporated in the buckling analysis.

Gardner [4] studied the influence of residual stresses on stainless steel structural members from the point of view of premature yielding and loss of stiffness. Existing data on residual stresses in stainless steel sections were examined and the data were used to develop models for predicting the magnitude and distribution of residual stresses in press braked, cold rolled, hot rolled, and fabricated stainless steel structural sections. The bending residual stresses are principally associated with the plastic deformation that occurs in section production, which also causes significant cold working. According to the developed models, it is proposed that membrane and bending residual stress to be taken as function of the yield strength of the material (σ0.2). For press braked stainless steel angles membrane residual stress magnitude may be taken as 0.14σ0.2 in the flat regions and 0.11σ0.2 in the corner regions, while bending residual stresses may be taken 0.15σ0.2 in the flat regions and 0.36σ0.2 in the corner regions, based on a rectangular stress block distribution. For rolled sections, residual stresses were found to be greater. Again based on characteristic values, the magnitude of membrane residual stresses can be taken as 0.37σ0.2 in the flat region and 0.24σ0.2 in the corner regions. Bending residual stresses may be taken as 0.63σ0.2 in the flat regions and 0.37σ0.2 in the corner regions, based on a characteristic rectangular stress block distribution.

Base material for cold formed steel sections is obtained by cold rolling of thick steel strips, reducing the thickness to the desired value. The cold rolled sheet material is generally coiled for easy storage and transportation. The forming process initiates with uncoiling and leveling of the sheet material, followed by cold rolling through a series of shaped rollers to produce the desired section. Using this process, the yielding and tensile strength are increased, while the material ductility decreases. The paper concludes that cold-formed sections created by press braking and cold rolling generally show low membrane residual stresses, but high bending residual stresses.

Wang et al. [5] employed neutron diffraction to investigate residual stresses in thin cold-rolled stainless steel sheet and to determine the influence of annealing the material. Measurements revealed highly directional intergranular residual stresses after the rolling process. Annealing to 500°C was found to significantly reduce this degree of alignment.

Quach et al. [6] carried out an analytical model study, validated against a finite-element study, to predict the residual stresses induced by the coiling, uncoiling and leveling of carbon steel material.

Schafer and Peköz [7] proposed a model for the prediction of bending residual stresses in cold-rolled carbon steel channel sections. Higher bending residual stresses were proposed for the web than for the flanges, supported by the experimental data of Weng and Peköz [8]. Membrane residual stresses were reported to be less than 0.08σy, with the highest values in the corner regions of the sections [7]. Based on the results of Weng and Peköz [8] and their own experimental data from two sizes of cold rolled lipped channels, Abdel-Rahman and Sivakumaran [9] proposed that the bending residual stresses in all flat regions could be modeled as 0.18σy, despite an observed variation with face width, and those of the corner regions could be approximated as 0.40σy.

The vast majority of experimental determination regarding residual stresses was carried out on simple C, U or hat cold rolled steel profiles. Experimental measurement of residual stresses on pallet rack upright cross-section presents a challenge due to the complex geometric shape. Taking a step further, two heavy duty pallet rack upright sections, RS125x3.2 and RS95x2.6, are examined hereafter.

2. EXPERIMENTAL PROGRAM

In order to determine the capacity of two pallet rack upright sections, i.e. RS125x3.2 and RS95x2.6, an extensive experimental program was developed within the CEMSIG Research Centre (http://cemsig.ct.upt.ro) of Politehnica University of Timisoara [10]. The overall geometric details of the studied sections are presented in Fig. (1).

Fig. (1). Sections under study.

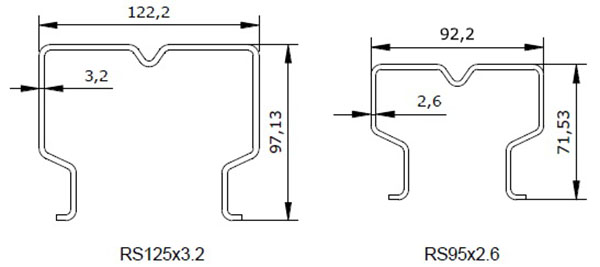
The sections were provided by the manufacturer without any protecting layer (nor galvanized, nor painted). The sectional dimensions were further measured in order to determine geometric deviations and actual base metal thickness. The geometry measurements were carried out using a sliding digital calliper with 0.01 mm resolution. The results of the geometric dimensions and imperfections, together with their interpretation are presented in detail in [10].

2.1. Yield Strength and Tensile Strength

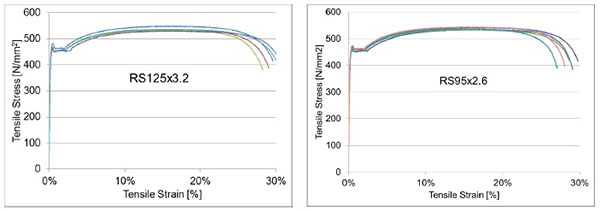
In order to determine the yield strength of base material, a total number of ten samples were tested, five for each base material thickness. A testing system, equipped with an optical extensometer, was used in order to determine the main mechanical characteristics and establish the behaviour curves (stress-strain diagram) for the base material together with relevant material properties (e.g. yield strength, tensile strength). The experimental tests were carried out in accordance to EN10002-1 provisions. In Table 1 are presented the mean values of base material properties for the two sections, RS125x3.2 and RS95x2.6.

Fig. (2). Behaviour curves of base material.
Table 1.
Mean value of base material properties.
Section Yield strength
[N/mm2] 		Young modulus
[N/mm2] 		Tensile strength
[N/mm2] 		Elongation at
maximum load [%]
RS125 465.18 202941.28 537.40 15.50
RS95 461.41 207463.67 538.90 15.77

The behaviour curves are presented in Fig. (2).

It is known that, the material in the corner areas of a section is cold-worked to a considerably higher degree than the material in the flat areas. In order to experimentally determine the yield strength and tensile strength increase over the cross-section, a new series of determinations on coupons cut from specimens without perforations were performed for the both studied sections.

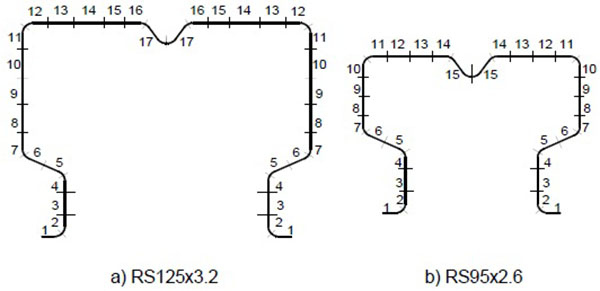
Three cold formed profiles were cut into strips, as presented in Fig. (3), for both RS125x3.2 and RS95x2.6 sections.

Fig. (3). Section partition.

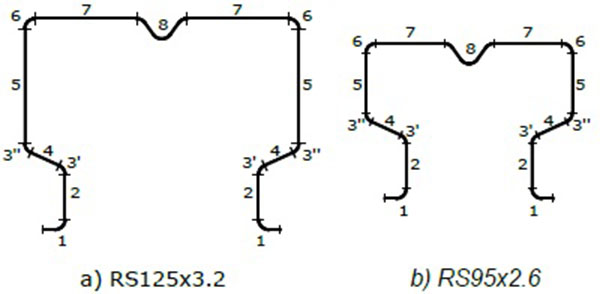
For these strips, the same testing protocol was used as for base material, in accordance to EN10002-1 provisions. The behaviour curves obtained for each strip are presented in Fig. (4), for both sections.

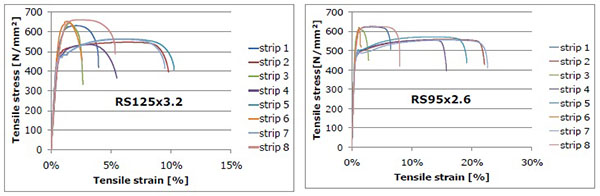
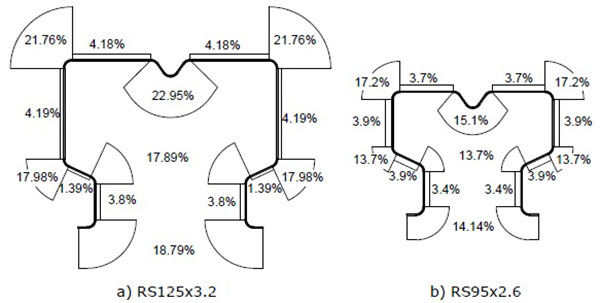
Fig. (4). Behaviour curves for cold rolled section strips.

It can be easily observed that the yield strength increase is not uniform across the section. In order to better depict this, the average yield strength increase due to cold forming process for studied upright sections is presented in Fig. (5) as percent of yielding strength of base material for each considered strip. Together with yield strength, the tensile strength is also affected by the cold forming process. In Fig. (6), the average increase in tensile strength, is presented for the two upright sections, RS125x3.2 and RS95x2.6, respectively.

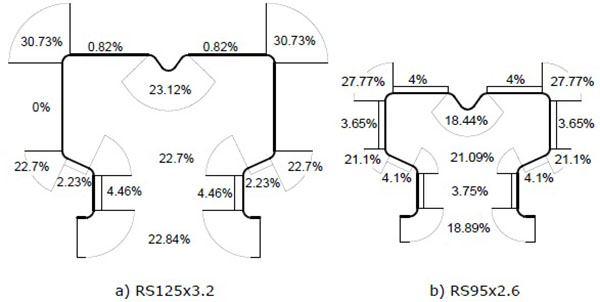
Fig. (5). Yield stress increase due to cold forming (%fy).
Fig. (6). Tensile strength increase due to cold forming (%fu).

It can be observed that even if the shape of RS125x3.2 section is in fact a scaled version of the RS95x2.6 section and the yield increase strength is similar, it is not identical. It can be concluded that the ratio of the sectional dimensions (width of flat areas) and thickness of the material plays an important role.

Comparing the results presented in Figs. (5 and 6), it can be observed that the tensile strength increased following the same pattern as the yield strength, but the increase is not the same.

2.2. Residual Stresses

As mentioned before, in case of cold formed steel sections, beside the increase of yield strength and tensile strength due to cold rolling, another important phenomenon must be considered i.e. the occurrence of residual stresses as a result of the cold forming process.

Theoretical residual stresses are composed of two types of residual stresses i.e. membrane and through the thickness (Schafer and Pekoz [7]). Membrane residual stresses were reported to be less than 0.08fy, with the highest values in the corner regions of the sections. For cold-formed steel members, residual stresses are dominated by a through thickness variation, i.e. bending residual stresses. This variation of residual stresses leads to early yielding on the faces of cold-formed steel plates. The residual stresses can be decisive in the evaluation of the ultimate load of a steel member.

In order to determine the distribution and magnitude of residual stress, a new set of coupons was prepared by cutting out of four cold formed sections (two for each section). Strips were cut, parallel with sections longitudinal axis, as presented in Fig. (7).

Fig. (7). Strips partition for residual stresses measurements.

The value of residual stresses was evaluated using the method proposed by J. Rondal [11]. The proposed method allows the determination of flexural residual stresses on both interior and exterior faces of cold formed profiles by direct geometric measurements of the curvature of a strip cut off from a profile. The method admits the hypothesis that the membrane residual stresses are zero, assuming a linear variation through the thickness. In reality, the membrane residual stresses exist, but for the case of cold formed sections, due to assumed linear variation through the thickness assumption, they are ignored.

For each cut strip, the curvature was measured using contactless optical measuring system. An example of the ISO surface results and polynomial approximation is presented in Fig. (8).

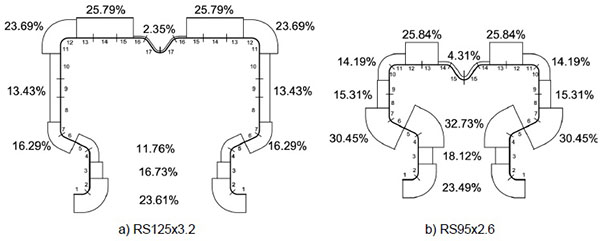
Fig. (8). Measured geometry and approximation function for residual stresses measurement.
Fig. (9). Residual stress distribution (%fy).

The average value of residual stress measurements is presented in Fig. (9), expressed as percent of fy. The diagrams are represented on the compressed side of the strip.

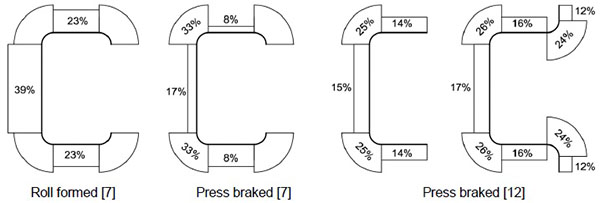
Since the experimental determination of residual stresses is a laborious and cumbersome procedure, Schafer and Pekoz [7] and Ungureanu [12] proposed an average residual stress distribution for cold formed sections, presented in Fig. (10).

Fig. (10). Average bending residual stresses (%fy).

2.3. Discussion

Considering the results presented in Figs. (2 and 4), it can be easily observed that the yield strength (Fig. 5) and tensile strength (Fig. 6) are increased across the entire cross-section. In the same time, the elongation at failure is significantly reduced. For corner areas, where the material is cold-worked to a considerably higher degree than the material in the flat areas, the ductility reduction is more significant (Fig. 4).

From the point of view of residual stresses, it can be observed (Fig. 9) that for section RS95x2.6 the bending residual stresses are higher than for RS125x3.2. This can be explained by the fact that the flat areas are smaller (distance between two subsequent corners), while the number of corners and corresponding angles are the same for both sections. Analogous, Ban [3] observed that the residual stress magnitude is significantly correlated with the width-thickness ratios of the legs for high-strength steel angle profiles.

Also, analysing Figs. (5, 6 and 9) it can be observed that the residual stresses distribution is different than the increase in the yield and tensile strength. The flat areas, develop relatively high residual stresses, while the yield and tensile strengths increase is very low.

In the case of studied pallet rack sections, the residual stress distribution proposed by Schafer and Pekoz [7] for rolled sections underestimates the residual stresses in corner areas.

2.4. Column Tests

Further, the experimental program was carried out in accordance with the specifications of the EN15512 [13] code. The complete experimental work was presented in Crisan et al. [14] and summarized hereafter.

The stub column tests were performed in order to observe the influence of perforations and the effects of local buckling on the ultimate strength of these members. They were carried out in accordance to Annex A.2.1.2 (Alternative 1) of EN15512 [13]. The length of specimens was taken to respect the code requirements i.e. (1) the length of specimen shall be three times the greatest flat width of the section (ignoring intermediate stiffeners); (2) it shall include at least five pitches of the perforations, at the midway between two sets of perforations. The base and cap plates shall be bolted or welded to each end of the stub upright. The end-devices, at both ends, consist of pressure pads 30 mm thick with an indentation of 5mm and a ball bearing of 40mm diameter.

In Table 2 are presented the ultimate loads of the tested stub columns together with associated failure mode.

Table 2.
Stub column tests: ultimate loads and failure modes.
RSBs125×3.2 RSNs125×3.2 RSBs95×2.6 RSNs95×2.6
F [kN] Failure
mode 		F [kN] Failure
mode 		F [kN] Failure
mode 		F [kN] Failure
mode
453.90
479.43
463.69
449.52
485.38
487.05		 413.28
407.81
400.85
404.03
402.27
400.19
397.46
409.05
411.02
396.51
395.91
406.05		 350.68
346.44
346.23
346.63
354.30
338.88		 279.82
276.99>
284.28
274.33
278.78
278.63
281.63
278.68
279.00
277.92
277.81
283.42

It is well known that the wavelength for distortional buckling is significantly longer than that for local buckling. This means that distortional buckling is not usually identified by a conventional stub-column test. Furthermore, if a stub-column test exhibits a distortional failure mode, it is unlikely that the length is sufficient to determine the minimum distortional buckling load. For RS125x3.2 sections, the failure can be classified as distortional deformations, while for RS95x2.6, in most cases the failure can be classified as squashing.

Further, the upright column tests were carried out in accordance with section 9.7.2 and Annex A.2.2 of EN15512:2009 [13] code. The tests were performed in order to determine the effects of the distortional buckling mode on the axial load capacity of the upright section. The same test arrangement and settings as for stub column tests described in the previous paragraph were used. According to European design code [13], the length of the specimens shall be equal to the length of the single bracing panel closest to one meter, i.e. 1200 mm in this particular case.

In Table 3 the ultimate loads for tested specimens are presented, for the two tested cross-sections, with and without perforations and the associated failure modes. For these tests, none of the tested specimens have failed in a local buckling mode. It was observed that for RS125x3.2 cross-sections the failure mode was distortional, while for members of RS95x2.6 cross-section, the observed failure modes were flexural about minor axis or flexural-torsional mode, or coupling of them.

Table 3.
Upright column tests: ultimate loads and failure modes.
RSB125×3.2 RSN125×3.2 RSB95×2.6 RSN95×2.6
F [kN] Failure
mode 		F [kN] Failure
mode 		F [kN] Failure
mode 		F [kN] Failure
mode
386.72
369.12
386.90
373.41
382.59		 347.26
363.48
350.79
339.09
326.42
337.18
354.40
350.45
340.54
345.41		 270.35
270.49
272.06
279.65
269.83		 207.18
215.72
209.87
211.29
206.45
213.24
223.33
216.30
208.90
209.91

3. NUMERICAL SIMULATIONS

3.1. Model Calibration and Validation

The numerical models applied to simulate the behaviour of studied sections, have been created using the commercial FE program, ABAQUS/CAE [15]. The numerical models were calibrated to replicate the physical tests. Rectangular 4-noded shell elements with reduced integration (S4R) were used to model the thin-walled cold-formed members. The chosen mesh size for the shell elements was around 5×5mm, in order to be able to model the corner radii. The material behaviour used for numerical modelling was defined in accordance with the experimentally recorded curves from uniaxial tensile tests from coupons cut over the cross-section and presented in previous sections.

The base plates and pressure pads were modelled using RIGID BODY with PINNED nodes constraints. The reference point for the constraints was considered to be the centre of the ball bearings (55mm outside the profile), in the gravity centre of the cross-section, as shown in Fig. (11). For numerical simulations, the specimens were considered pinned at one end and simply supported at the other one. For the pinned end, all three translations together with the rotation along the longitudinal axis of the profile were restrained, while the rotations about maximum and minimum inertia axes were allowed. For the simply supported end, the translations along section axis and the rotation about longitudinal profiles axis were restrained, while the rotations about major and minor inertia axis together with longitudinal translation were allowed.

Fig. (11). End constraints.

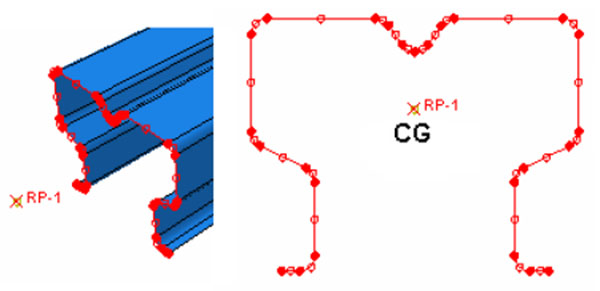
The pinned end was considered to replicate the end support of the real tested specimen, while the simply supported end was considered to reproduce the loading machine end, allowing for direct force/displacement specification.

The analysis was conducted in two steps. The first step consists of an eigen buckling analysis (LBA), performed to find a buckling mode or combination of buckling modes, affine with the relevant measured imperfections. After imposing the initial geometric imperfection, obtained as a linear combination of eigen buckling modes from the previous step, a GMNIA (Geometrically and Materially Nonlinear Analysis with Imperfections) analysis with arc-length (static, Riks) solver was used to determine the profiles ultimate capacity.

Table 4 presents the experimental and numerical compressive failure loads, while Fig. (12) presents the characteristic failure modes for experimentally tested and numerically simulated specimens.

Table 4.
Mean value of base material properties.
Test
type 		Section
type 		RS125×3.2 RSBs95×2.6
Test FEA Test FEA
Stub No perforations 487.05 486.13 338.88 335.15
With perforations 411.02 422.98 274.33 272.01
Uptight No perforations 386.72 384.40 279.65 285.96
With perforations 347.26 344.00 223.33 231.89
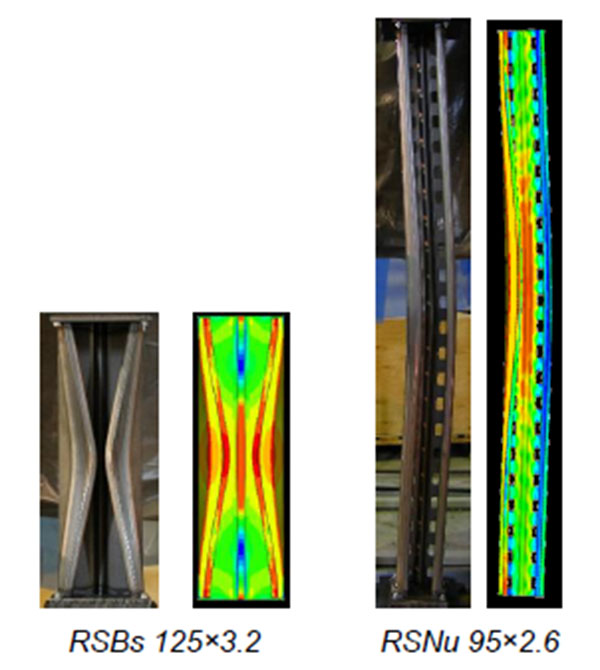
Fig. (12). Characteristic failure model.

Based on the results obtained from numerical simulations, it can be noted that from the point of view of maximum load, the numerical model is able to accurately replicate the experimental tests.

3.2. Effects of the Cold Rolling Process

The effects of geometric imperfections i.e. sectional, global and loading eccentricities, together with their combination were presented [16] and will not be considered in present study.

Using calibrated numerical models, the effects of residual stresses, measured experimentally for RS125x3.2 and RS95x2.6 were studied for a relative slenderness ranging from about 0.1 to 1.9. The stresses were modelled using *initial conditions, stress option in Abaqus.

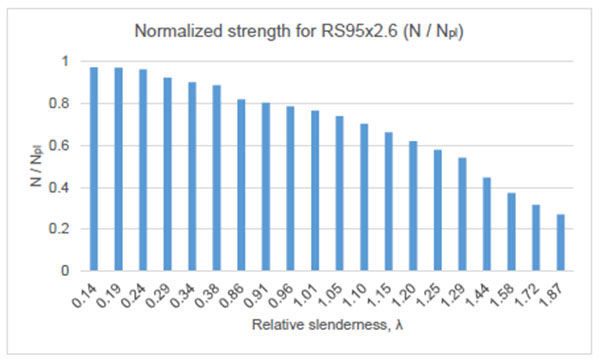
In Figs. (13 and 14) the normalized strength obtained for the RS125x3.2 and RS95x2.6 sections with residual stress are presented. The normalized strength, 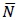, was computed using 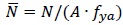where N is the ultimate load considering the residual stresses, A is the gross section area and fya is the yield strength averaged over the section.

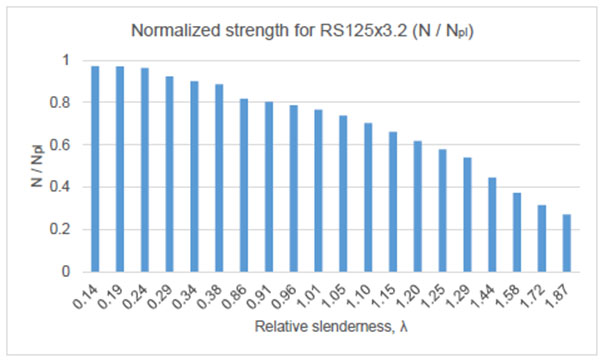
Fig. (13). Normalized Strength for RS125x3.2.

It can be argued that the values obtained following the numerical analyses are higher than the experimental ones. This increase arises due to the fact that, for these analyses, the geometric imperfections were not considered.

Fig. (14). Normalized Strength for RS95x2.6.
Fig. (15). The interactive buckling model based on the ECBL theory.

3.3. Erosion Evaluation

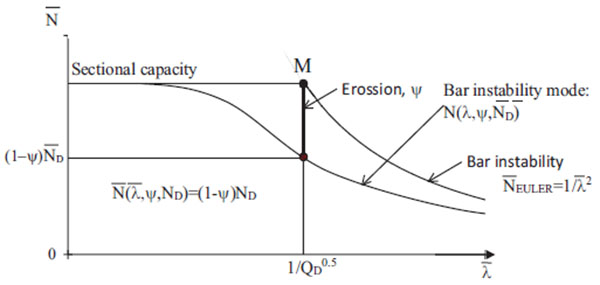
The concept of erosion is explained in detail by Dubina [17] and briefly presented in Fig. (15). Dubina et al. [18] also presented the experimental evidence of erosion of critical buckling load in interactive bucking, presenting the background and the approach for erosion evaluation.

In Fig. (15) the following notations where used: 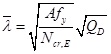, , 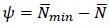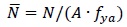where N is the ultimate load considering the residual stresses, 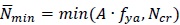, 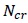is the minimum critical buckling load for distortional or flexural buckling.

Fig. (16). Erosion factors for RS125x3.2.

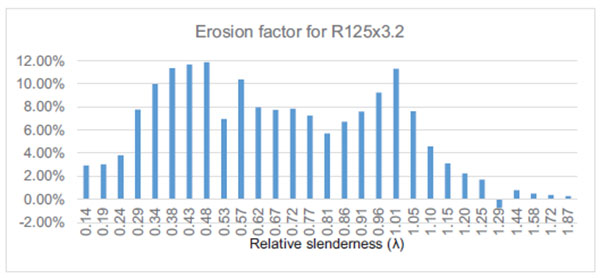
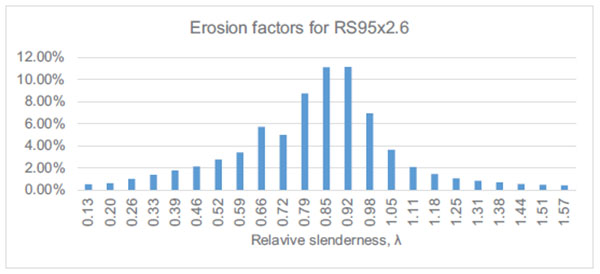
Further, the erosion, 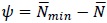, was used to evaluate the effect of residual stresses on the element strength. Using this approach, the erosion factors were computed for RS125x3.2 and RS95x2.6 respectively. The results are presented in Figs. (16 and 17).

Fig. (17). Erosion factors for RS95x2.6.

In case of relatively long columns ( 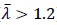) the effects of residual stresses is reduced, while the global buckling becomes the general failure criteria.

It can be observed, for both sections, that the effects of residual stresses is relatively small for short columns ( 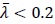) and in case of RS125x3.2 section the effects of residual stresses is larger than for RS95x2.6 section Figs. (16 vs. 17). The difference can be explained by the fact that for RS125x3.2 profile, the sectional capacity is given by distortional buckling, while for RS95x2.6 profile, the sectional capacity is given by the plastic strength, residual stresses destabilizing the section.

For both sections, in intermediate length range, the effects of residual stresses is shown to have an important effect (>10%), reducing the element’s capacity.

CONCLUDING REMARKS

The current paper presents the effects of cold rolling process on two heavy duty pallet rack uprights. Besides the increase in yielding stress and tensile strength, the distribution of residual stresses is presented. For studied sections, the measured residual stresses pattern is different than the increase in yield and tensile strength due to cold forming.

Further, using numerical models calibrated against experimental results, the effect on yield stress and tensile strength together with the effect of flexural residual stresses were investigated. Based on numerical results it can be said that for short stub columns ( 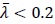), the effect of residual stresses is negligible. Also, for long elements, where the strength is governed by global buckling, the effect of residual stresses is negligible. For intermediate lengths, the residual stresses can cause an erosion of more than 10%, which can be classified as class II, moderate erosion [19].

CONFLICT OF INTEREST

The authors confirm that this article content has no conflict of interest.

ACKNOWLEDGEMENTS

This work was partially supported by the strategic grant POSDRU/159/1.5/S/137070 (2014) of the Ministry of Labour, Family and Social Protection, Romania, co-financed by the European Social Fund – Investing in People, within the Sectorial Operational Programme Human Resources Development 2007-2013.

REFERENCE

1 S.D. Hu, L.X. Li, X.Y. Wang, and Q.M. Chang, "Experimental study and design calculation for compressive strengths of cold formed thick‐wall sections", Mater Res Innovat, vol. 15, no. s1, pp. 450-453, 2011.
[CrossRef Link] 2 A. H. Yaghi, T. H. Hyde, A. A. Becker, and W. Sun, "Finite element simulation of welding residual stresses in martensitic steel pipes", J. Mater. Res. Innovations, vol. 17, no. 5, pp. 306-311, 2013.
[CrossRef Link] 3 H. Ban, G. Shi, Y. Shi, and Y. Wang, "Residual stress tests of high-strength steel equal angles", J. Struct. Eng., vol. 138, no. 12, pp. 1446-1454, 2012.
[CrossRef Link] 4 L. Gardner, and R. Cruise, "Modeling of residual stresses in structural stainless steel sections", J. Struct. Eng., vol. 135, no. 1, pp. 42-53, 2009.
[CrossRef Link] 5 Y.D. Wang, R.L. Peng, X.L. Wang, and R.L. McGreevy, "Grain-orientation-dependent residual stress and the effect of annealing in cold-rolled stainless steel", Acta Mater., vol. 50, no. 7, pp. 1717-1734, 2002.
[CrossRef Link] 6 W.M. Quach, J.G. Teng, and K.F. Chung, "Residual stresses in steel sheets due to coiling and uncoiling: A closed form analytical solution", Eng. Struct., vol. 26, no. 9, pp. 1249-1259, 2004.
[CrossRef Link] 7 B.W. Schafer, and T. Peköz, "Computational modelling of cold-formed steel characterising geometric imperfections and residual stresses", J. Constr. Steel Res., vol. 47, pp. 193-210, 1998.
[CrossRef Link] 8 C.C. Weng, and T. Peköz, "Residual stresses in cold formed sections", J. Struct. Eng., vol. 116, no. 6, pp. 1611-1625, 1990.
[CrossRef Link] 9 N. Abdel-Rahman, and K.S. Sivakumaran, "Material properties models for analysis of cold-formed members", J. Struct. Eng., vol. 1239, pp. 1135-1143, 1997.
[CrossRef Link] 10 A. Crisan, "Buckling Strength of Cold Formed Steel Sections Applied in Pallet Rack Structures", PhD. Thesis (Scientific coordinator: prof. dr. ing. Dan Dubina, Editura POLITEHNICA, Seria 5, nr. 76, 2011. 11 J. Rondal, Determination Theoretique Des Contraintes Residuelles Dans Les Elements En Acier Profiles a Froid. Ce travail a Recu Le Prix N.V. BEKAERT S.A. 1992, Octroye Par Le Fonds National De La Recherche Scientifique, 1992. 12 V. Ungureanu, Contribuţii La Studiul Flambajului Prin îNcovoiere-răSucire a Grinzilor Din Profile Cu Pereţi Subţiri, 2003. 13 EN15512, Steel Static Storage Systems - Adjustable Pallet Racking Systems - Principles for Structural Design., CEN: Brussels, 2009. 14 A. Crisan, V. Ungureanu, and D. Dubina, "Behaviour of cold-formed steel perforated sections in compression. Part 1—Experimental investigations", Thin-walled Struct., vol. 61, pp. 86-96, 2012.
[CrossRef Link] 15 ABAQUS, Theory manual., Hibbit, Karlson and Sorenson Inc., 2007. 16 A. Crisan, U. Ungureanu, and D. Dubina, "Behaviour of cold-formed steel perforated sections in compression: Part 2-numerical investigations and design considerations", Thin Wall. Struct., vol. 61, pp. 97-105, 2012. 17 D. Dubina, "The ECBL approach for interactive buckling of thin-walled steel members", Steel Compos. Struct., vol. 1, no. 1, pp. 75-96, 2001.
[CrossRef Link] 18 D. Dubina, V. Ungureanu, and A. Crisan, "Experimental evidence of erosion of critical load in interactive buckling", J. Struct. Eng, vol. 139, no. SPECIAL ISSUE: Cold-Formed Steel Structures, pp. 705-716, 2013. 19 G. Victor, "General theory of coupled instability", Thin-walled Struct., vol. 19, no. 2-4, pp. 81-128, 1994.