All published articles of this journal are available on ScienceDirect.
On the Origin of I Beams and Quick Analysis on the Structural Efficiency of Hot-rolled Steel Members
Abstract
Background:
In the current paper the origin of steel I beams has been analysed from historical-technological and structural points of view.
Method:
First, the way leading to discover the most famous structural member of the modern Steel Engineering has been reconstructed. Later on, parameters of structural efficiency, allowing for a quick numerical evaluation of the effects produced by the rolling process on the semi-finished casting products, have been defined as a function of the difference in terms of weight between the solid billet and the member final shape on the basis of the more or less raw material centrifugation. By using the above mentioned structural efficiency parameters, the design criteria used for development of the European list of sections, with particular reference to IPE and HE profiles, have been comprehended.
Result and Conclusion:
Finally, the proposed method, if applied to members having the same area, allows defining, without considering local buckling phenomena, the best profile for each performance category of steel members.
1. INTRODUCTION
Widely used as member with either wide or narrow flanges subjected to bending moment and/or axial forces, the undisputed star of the steelwork is certainly the I profile, defined according to the code EN 10079:2007 [1] as I (narrow flanges – see §3.4.7.1) or H (wide flanges – see §3.4.7.4.2) beam. This standard defines I-beams each long shape hot-rolled profile with a geometrical configuration similar to the letter I, where the flanges have a width (b) not exceeding 0.66·h (h=depth) and, in any case, less than 300 mm. On the other hand, the H-beams are profiles with flanges larger than 0.66·h (or 300 mm) or more. Sections with flanges wider than 0.80·h are sometimes called either columns or profiles with effective wide flanges.
How the concept was born and who invented this section? Unquestionably it can be regarded as one of the innovative products of the industrial revolution, but it is not easy to give an immediate answer to this question, because its origins are to be found in different areas of the emerging modern Engineering. In any case, rather than from a theoretical study on the material optimization resulted from the application of methods and models developed by eminent scholars of that time, such as Claude-Louis Navier, with the technical theory of the beam subjected to flexural bending moment published in 1826, the idea of the I profile and its evolution draws inspiration from both the experience and the technological progress. In the present paper a contribution on both the genesis of I section profiles and the structural efficiency of such members is provided, it being justified by the wide use of such sections into the most common seismic-resistant steel typologies [2-5]. Therefore, some expeditious efficiency parameters, able to both evaluate the section structural performance with respect to the starting semi-finished product and assess the effects produced by the rolling process, have been defined. These parameters will also permit to compare from the performance point of view different profiles belonging to the same list of sections (e.g. comparison among European profiles) or framed within different lists (e.g. comparison between European profiles and American ones). Finally, the same parameters will allow to directly identifying the optimal profile related to both a specific performance feature and a used category. Such a procedure can be also applied in the design phase for optimization of either complex tailor-made hot-rolled profiles or cold-formed ones [6-8].
2. HISTORICAL BACKGROUND
The I profile was born in the railway field through the realization of the train tracks, originally constructed under form of wood prismatic elements with a metal band at their extrados having the function of a rolling plane.
For durability reasons, in 1789 these types of profiles were replaced by the English engineer William Jessop with cast-iron elements characterized by an embryonic I section composed of two bulbs and a web. Technological reasons linked to the low productivity of the production process, together with the reduced tensile strength of the material, strongly decreased their use, so as to be completely displaced by the advent of the first hot-rolled steel products. Starting from the T-section, the first iron or laminated steel rails suffered a fast evolutionary process, early attaining the current configuration of the wide flange I profile, known as Vignoles rail and devised in 1831 by the American colonel Robert L. Stevens [9].
Almost simultaneously to the railway applications, the I profile was introduced in the shipbuilding and civil fields. The pioneer in both fields was the Scotsman Sir William Fairbairn who, taking profit of the scientific consultant activity given by the English engineer Eaton Hodgkinson, performed in the 30's theoretical and experimental investigations aimed at choosing the optimal profile to be used for both cast iron full beams for railway crossings and hot-rolled steel stiffening ribs for hulls of boats. The results achieved by Fairbairn and Hodgkinson were also usefully employed in the civil construction sector, in particular for the erection of long-span bridges.
From the mid-nineteenth century, with the development of the hot-rolling production process, the I profiles were used in the construction of residential and industrial buildings by replacing both the previously used wooden rectangular or circular members and the cast iron T-sections, the latter introduced in early 1800 by James Watt [10].
3. DESIGNATION AND STANDARDIZATION
The diffusion of hot-rolled sections with I profiles into different fields of engineering was such that their production was standardized from the beginning through the definition of predefined types and sizes.
Although already in the early 60's of the XIX Century there was an extensive range of profiles produced on industrial scale, the unification process leading to the first list of I cross-sections, conducted at the national level (e.g. in Germany, France and Italy), ended only in the 20’s of the subsequent century with the production of “Normal Profiles”, marked by the letters “PN” or “NP”.
A direct testimony is contained in the manuals of that time (Colombo, 1877 [11], Boubée, 1880 [12] and Breymann, 1925 [13]), where the first lists of I profiles with tapered flanges, called IPN, were mentioned. A rigorous study on materials and products used in steelworks from origins (early '800) up to 1950 was conducted by both the American Institute of Steel Constructions [14] and the British Constructional Steelwork Association [15].
Subsequently, from the establishment of the European Community on Coal and Steel (ECSC) (1951), the unification process of hot-rolled profiles was done in Europe, alongside the normal series with the “European Profiles” having not tapered flanges, marked by initials “PE” or simply “E”.
Since the ‘60s, through European standards EU 19-57 and 53-62, respectively, European double T profiles with narrow flanges (IPE) and wide flanges (HE) were born, they being discernible with a number identifying their height (h) expressed in millimetres. Since the '70s, using the same rolling mills, but making small movements on the position of the rollers, heavy (marked with M or O) and light (marked with A) series of I cross-sections were included in the European list of profiles together with the standard series profiles.
4. STRUCTURAL PREREQUISITES AND EFFICIENCY RATIOS
The structural efficiency observed experimentally by Fairbairn can be easily demonstrated and quantified through the theory of beams under bending moments developed by Navier and generalized later by Barrè de Saint Venant. The secret of the I profile is in fact linked to the high “centrifugation” of the material generated by the rolling process (Fig. 1) that, for equal material used, allows to significantly increase the second moment of area of the section with respect to one of the main directions, identified with the strong axis (y-y axis). Starting from a semi-finished product with a square section (billet or bloom), the cross-section area is in fact transferred from the central area to the periphery (Fig. 2), going to delineate the two typical horizontal lintels (known as wings or flanges, characterized by an area from 50% to 75% of the total profile one) and the vertical connection element (web).

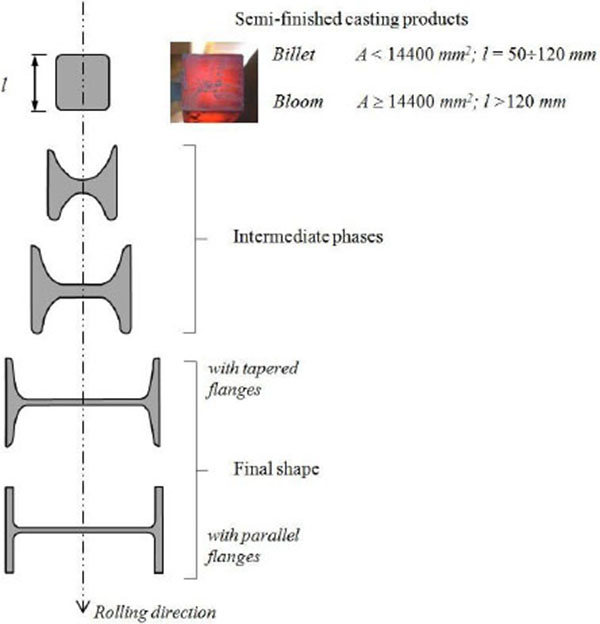
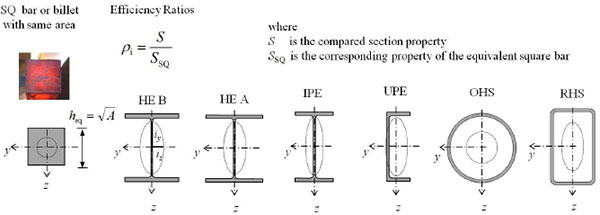
The morphological transformations, generated by the rolling process, contribute to increase the flexural performance of the structural element [16-21], modifying at the same time the structural behaviour. As it is known, in the I beams, the flanges are the member parts able to withstand the bending moment (over 80%), while the web has the task of absorbing mainly the shear stresses associated with the flexural regime. The passage from a compact section to a thin-walled open one (mono-connected section) produce, by contrast, a significant reduction in terms of stiffness and resistance to torsion stresses. A qualitative and quantitative comparative analysis about the performance of profiles can be performed through the use of appropriate “efficiency ratios” (ρS = S/SSQ), which express the effect of the working process, namely the raw material centrifugation, on both the section geometric properties (S) and the related structural performance, assessed against the starting semi-finished product (geometric properties of either the billet or the equivalent square section SSQ) having the same area (A), that is the same weight and unit cost (Fig. 3).
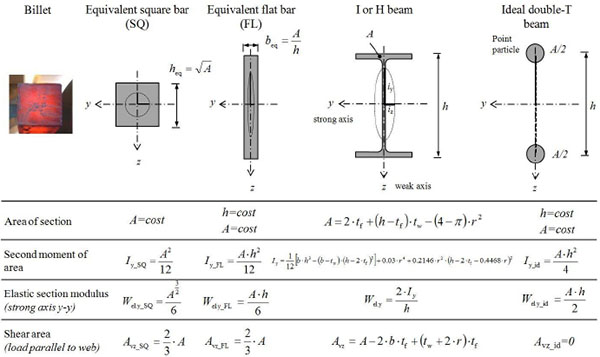
With respect to the geometric properties to be analysed, from the beam technical theory it is recalled that the section second moment of area along the strong axis (Iy) is directly correlated to the flexural performance in terms of deformability, which is associated to the so-called Serviceability Limit States (SLS) in terms of vertical (elastic deflection) and horizontal (drift) displacements. The elastic section modulus (Wy = Iy/(h/2)) is related to the bending strength, whereas the shear area (Avz), very close to the web area (Aw), is linked to the shear strength. The total strength capacity of flexural steel members against the Ultimate Limit State (ULS) is dependent from these parameters.
For steel profiles, the second moment of area along the vertical axis (z-z), the so-called weak axis, is instead indicative of their buckling performance (Ultimate Limit State for instability) in the cases when they are compressed (flexural buckling) or subjected to bending moment (flexural-torsional buckling or twisting).
Moreover, the torsional behaviour at the Ultimate and Serviceability Limit States is correlated to the torsion constant (IT) and to the warping constant (Iw), the latter in the case of non-uniform torsion.
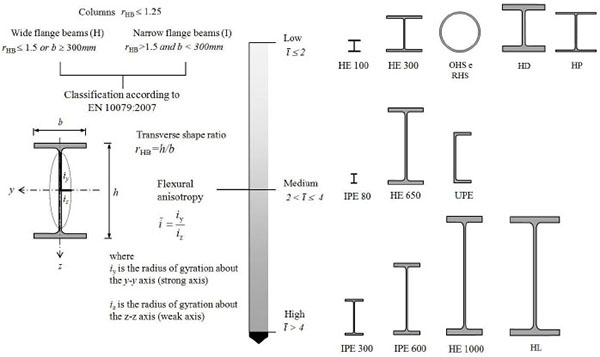
Finally, it should be remembered that the section centrifugation in the different directions is graphically represented by the central ellipse of inertia, which can be considered as a sort of polar diagram of the inertia (I = A·i2). The relationship between the two main radii of gyration (ī =iy / iz) expresses the “flexural anisotropy” of the section, namely the probable inequality in terms of the material disposal between the strong axis and the weak axis. Together with the transverse shape ratio (rHB=h/b, h and b being the depth and the width of the profile, respectively) that, as mentioned earlier, the EN 10079 code uses to differentiate the profiles with narrow flanges (rHB > 1.5 e b < 300mm) from those with wide flanges (rHB ≤ 1.5 or b ≥ 300mm), this parameter, other than being correlated to the section morphology, provides useful indications on the optimal use of profiles as compressed elements subjected to instability (flexural or flexural-torsional) phenomena.
For a given profile having the same buckling length (L0) in the two main planes (L0,y=L0,z), the flexural anisotropy (ī) coincides with the ratio between the member geometrical slenderness (λ=λ0/ι) related to the strong axis (λy) and that of the weak axis (λz). On the basis of this ratio the profiles can be divided into three categories: sections with low (ī≤2), medium (2<ī≤4) and high (4<ī) anisotropy. In the absence of intermediates supports, i.e. provided by diagonal bars or bracing systems, the use of high anisotropy sections should be avoided for compressed member that do not allow, due to onset of premature global instability phenomena, an adequate exploitation of the base material.
Under a general point of view, before carrying out the analysis of individual profiles, it is possible to observe that, if the profile grows in homothetic way, that is maintaining unaltered its proportions, its structural efficiency (ρS) does not change, it depending on the geometrical characteristics of the original profile. On the contrary, if the profile retains its outer shape (width b and depth h or diameter d), the flexural efficiencies (ρIy =Iy/Iy_SQ; ρWy = Wel.y/Wel,y_SQ, Iy,SQ and Wel,y_SQ being the second moment of area and the elastic section modulus of the equivalent square section, respectively) decrease with increasing thickness of both the web (tw) and the flanges (tf), tending to degenerate into the starting semi-finished product.
The profiles of the European list of sections (Fig. 4) are designed, as the height (and/or area) is increasing, with flexural efficiency augmenting according to the strong axis in terms of both strength and deformability. For narrow flanges I profiles (Table 1, Figs. 5 and 6) belonging to the IPE series, the efficiency in terms of flexural deformability (ρIy) varies from 16 to 45 with increasing height from 80mm (IPE80) to 600mm (IPE600), respectively. This parameter, with increasing height, instead varies from 8 to 48 for wide flanges HEB series profiles.
| Section type | Depth | Square section depth | Area of section | Flexural efficiency | Shear efficiency | |||
|---|---|---|---|---|---|---|---|---|
| Strong axis y-y | ||||||||
| SLU | SLE |
ρAv= Av,z/Avz_SQ |
||||||
| h (mm) | hSQ(mm) | A (mm2) | ρWy= Wel.y/Wel,y_SQ |
ρIy= Iy/Iy_SQ |
||||
| Open sections | HEA | HE 100 A | 96 | 46,1 | 2124 | 4,5 | 9,3 | 0,53 |
| HE 120 A | 114 | 50,3 | 2534 | 5,0 | 11,3 | 0,50 | ||
| HE 300 A | 310 | 106,1 | 11253 | 6,3 | 17,3 | 0,50 | ||
| HE 600 A | 590 | 150,5 | 22646 | 8,4 | 33,0 | 0,62 | ||
| HE 1000 A | 990 | 186,2 | 34685 | 10,4 | 55,2 | 0,80 | ||
| HEB | HE 100 B | 100 | 51 | 2604 | 4,1 | 8,0 | 0,52 | |
| HE 300 B | 320 | 122,1 | 16134 | 5,5 | 13,6 | 0,48 | ||
| HE 600 B | 600 | 164,3 | 26996 | 7,7 | 28,2 | 0,62 | ||
| HE 1000 B | 1000 | 200 | 40005 | 9,7 | 48,3 | 0,80 | ||
| IPE | IPE 80 | 80 | 27,6 | 764 | 5,7 | 16,5 | 0,70 | |
| IPE 180 | 180 | 48,9 | 2395 | 7,5 | 27,6 | 0,70 | ||
| IPE 400 | 400 | 91,9 | 8446 | 8,9 | 38,9 | 0,76 | ||
| IPE 600 | 600 | 124,9 | 15598 | 9,5 | 45,4 | 0,81 | ||
| UPE | UPE 80 | 80 | 31,8 | 1010 | 5,0 | 12,6 | 0,60 | |
| UPE 180 | 180 | 50,1 | 2510 | 7,2 | 25,8 | 0,67 | ||
| UPE 400 | 400 | 95,9 | 9190 | 7,1 | 29,8 | 0,92 | ||
| Hollow sections | OHS | OHS 21,3x2,5 | 21,3 | 12,2 | 148 | 2.1 | 3.6 | 0,96 |
| OHS 139,7x6 | 139,7 | 50,2 | 2520 | 3,9 | 10,8 | 0,96 | ||
| OHS 406x10 | 406,4 | 111,8 | 12500 | 5,2 | 18,8 | 0,96 | ||
| OHS 1219x10 | 1219 | 194,9 | 38000 | 9.2 | 57.7 | 0,96 | ||
| OHS 1219x20 | 1219 | 274,4 | 75300 | 6,5 | 28,7 | 0,96 | ||
| RHS | RHS 40x20x2,5 | 40 | 16,1 | 259 | 3,3 | 8,3 | 1,00 | |
| RHS 140x80x6 | 140 | 49 | 2400 | 4,3 | 12,4 | 0,96 | ||
| RHS 200x100x8 | 200 | 65,7 | 4320 | 4,4 | 13,4 | 1,00 | ||
| RHS 400x200x8 | 400 | 95,5 | 9120 | 6,5 | 27.3 | 1,00 | ||
| RHS 400x200x12 | 400 | 114,9 | 13200 | 5,2 | 18,0 | 1,00 | ||
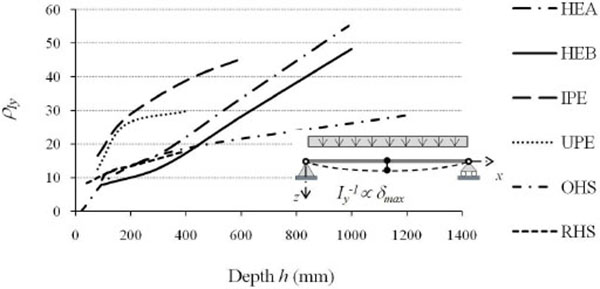
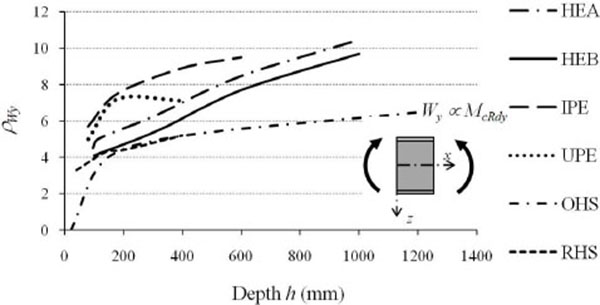
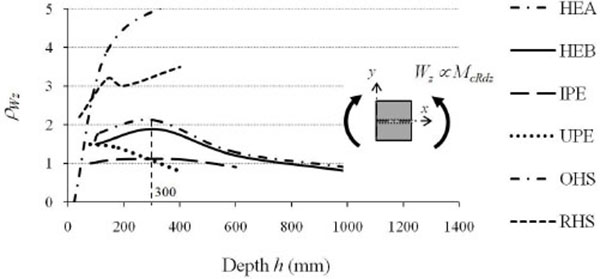
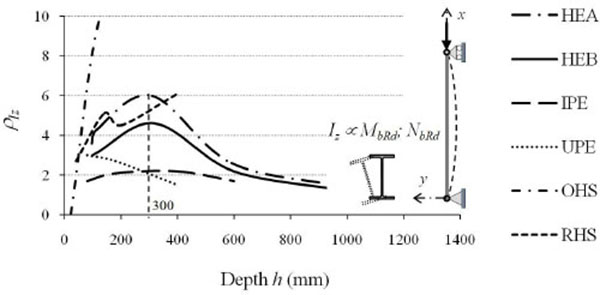
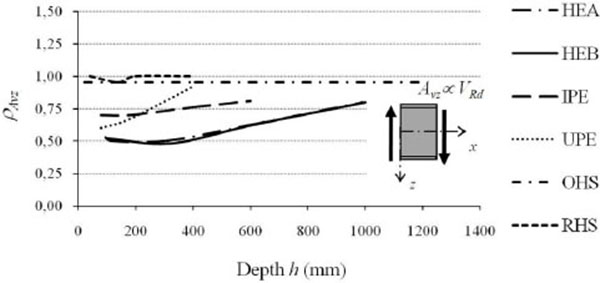
The increase of the flexural efficiency is even greater for wide flanges HEA profiles that, moving from HE100A to HE1000A, have ρIyvariable from 9 to 55. Less marked are the efficiency increments in terms of resistance (ρWy), that is the increments in terms of the elastic section modulus which, on average, increased from 4 to 10 times the performance of the equivalent square profile with increasing height. By analyzing the behaviour with respect to the weak axis (Table 2, Figs. 7 and 8), the flexural efficiency (ρIz=Iz/Iz,SQ), related to problems of global flexural and flexural-torsional instabilities, is not strictly increasing, but has a maximum for profiles with height equal to about 300mm. This is particularly true for wide flanges I profiles of the HE series. The loss of efficiency around weak axis for medium-large height profiles (h> 300 mm), although to a lesser extent, is also found for IPE series profiles. In all profiles with full web enclosed within the section list, the thinning of the section in the vicinity of the web reduces from 20% to 40% the profile shear strength in comparison to the equivalent square section, with efficiency (ρAvz=Avz/Av,SQ) increasing from 0.6 to 0.8 with the member height (Table 1, Fig. 9).
| Section type | Flexural efficiency | St. Venant Torsional efficiency | Flexural anisotropy | |||
|---|---|---|---|---|---|---|
| Weak axis z-z | ||||||
| SLU | SLE-SLUinst |
ρIt= It/It_SQ |
ī=iy/iz | |||
|
ρWz= Wel.z/Wel,z_SQ |
ρIz= Iz/Iz_SQ |
|||||
| Open sections | HEA | HE 100 A | 1,6 | 3,6 | 0,08 | 1,6 |
| HE 120 A | 1,8 | 4,3 | 0,07 | 1,6 | ||
| HE 300 A | 2,1 | 6,0 | 0,05 | 1,7 | ||
| HE 600 A | 1,3 | 2,6 | 0,06 | 3,6 | ||
| HE 1000 A | 0,9 | 1,4 | 0,05 | 6,3 | ||
| HEB | HE 100 B | 1,5 | 3,0 | 0,10 | 1,6 | |
| HE 300 B | 1,9 | 4,6 | 0,06 | 1,7 | ||
| HE 600 B | 1,2 | 2,2 | 0,07 | 3,6 | ||
| HE 1000 B | 0,8 | 1,2 | 0,06 | 6,3 | ||
| IPE | IPE 80 | 1,0 | 1,7 | 0,09 | 3,1 | |
| IPE 180 | 1,1 | 2,1 | 0,06 | 3,6 | ||
| IPE 400 | 1,1 | 2,2 | 0,05 | 4,2 | ||
| IPE 600 | 0,9 | 1,7 | 0,05 | 5,2 | ||
| UPE | UPE 80 | 1,5 | 3,0 | 0,10 | 2,0 | |
| UPE 180 | 1,4 | 2,7 | 0,08 | 3,1 | ||
| UPE 400 | 0,8 | 1,5 | 0,07 | 4,5 | ||
| Hollow sections | OHS | OHS 21,3x2,5 | 2.1 | 3.6 | 4,32 | 1,0 |
| OHS 139,7x6 | 3,9 | 10,8 | 12,64 | 1,0 | ||
| OHS 406x10 | 5,2 | 18,8 | 22,28 | 1,0 | ||
| OHS 1219x10 | 9.2 | 57.7 | 68,36 | 1,0 | ||
| OHS 1219x20 | 6.5 | 28.7 | 33,97 | 1,0 | ||
| RHS | RHS 40x20x2,5 | 2,2 | 2,7 | 4,30 | 1,8 | |
| RHS 140x80x6 | 3,2 | 5,1 | 7,21 | 1,6 | ||
| RHS 200x100x8 | 3,0 | 4,5 | 6,90 | 1,7 | ||
| RHS 400x200x8 | 4.5 | 9.4 | 13,53 | 1,7 | ||
| RHS 400x200x12 | 3,5 | 6,1 | 9,30 | 1,7 | ||
As further reversal of the medal, the lamination process strongly reduces the torsional efficiency of open shape profiles, characterized by torsion constant (IT) equal to just 5÷10% of that of starting semi-finished products (Table 2, Fig. 10).
Finally, the increase of the transverse shape ratio proportionally to the profile height is reflected directly on the flexural anisotropy parameter. As it is seen in Fig. (11), HE profiles may be considered “actually” as wide flanges cross-sections if flexural anisotropy is medium-low. In fact, members with heights greater than 600 ÷ 650 mm have ratios between radii of gyration larger than 4, which is very different slenderness values along two main axes. Regardless from their size, a low anisotropy is instead shown by both hollow profiles and new HD (wide flanges columns) and HP (wide flange bearing piles) profiles, whose use is particularly recommended for highly stressed compressed members, e.g. located in tall buildings and foundation piles.
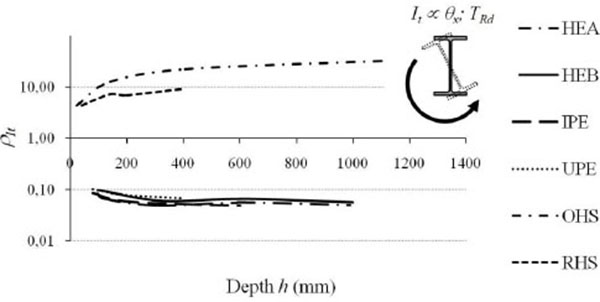
On the other hand, HE profiles with heights greater than 600mm, similarly to IPE profiles, are particularly suitable for the production of elements subjected to bending moment and located into buildings having floors with medium-large bays. In these cases, also the recent HL profiles (extra wide flanges beams) may be adopted. In comparison to HE members, these profiles, although having a high flexural anisotropy, ensure a greater lateral stability due to the greater width of the flanges, whose size for the entire series is equal to about 400 mm.
Neglecting the onset of possible local or global buckling phenomena, the increase of flexural efficiency (ρIy; ρWy) as the cross-section height augments gives rise, within the design phase, to an apparent “paradox”, that is the realization of always slenderer members with longitudinal shape ratios (rHL=h/L, h and L being the depth and the length of the profile) gradually decreasing with the member length.
As an example, for floor-decking of civil residential buildings (permanent loads gk=4kN/m2and service loads qk=2kN/m2 - Cat. A) made of steel corrugated trapezoidal sheeting and composite slabs (Fig. 12), the secondary beams, placed each to other at a distance i = 1.5÷2m, can be pre-designed (h(L) =rHL·L) (Fig. 13) with depth/span ratio rHL variable from 1/20 to 1/25 for members of small (L = 3m) and medium-large (L = 7÷10m) lengths, respectively. The shape ratios for sizing main beams posed with pitch iTP variable from 5m to 7m, decreased from 1/15 to 1/20 when beams of small (L = 5 m) or large (L = 15m÷20m) lengths are of concern, respectively (Fig. 14).
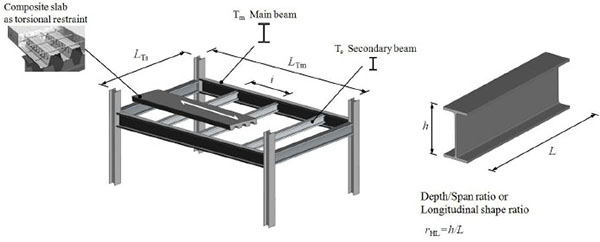
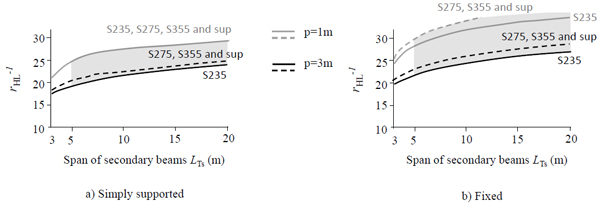

This is explained by the fact that, despite the increase of the length (L), the vertical displacements (δ) of a steel member in bending subjected to a uniformly distributed load grow with the fourth dimension of the length and bending moments (MEd) grow with the length square dimension, so that the related inertial characteristics (Iy and Wy) grow, for the above-mentioned increase of efficiency (ρs), in an even more marked way with the required height necessary to meet the design requirements.
5. SELECTION OF OPTIMAL CROSS-SECTION FOR DIFFERENT APPLICATION FIELDS
The structural efficiency parameters, other than providing useful indication about the effects produced by the rolling process on the cross-section geometrical properties, if applied to members with the same area (A), or the same weight (Gk) and cost per metre linear, enable to directly identify the optimal profile for performance feature and utilization category (beams under bending moment, beams subjected to torsion, compressed and compressed-flexural columns).
Taking as a benchmark example a billet or a semi-finished shape with square section of 50mmx50mm (cross-section A = 2500mm2), the structural performances of hot-rolled profiles HE100B, HE120A, IPE180 and UPE180 can be compared (Fig. 15). When possible buckling phenomena are prevented, for example by adopting specific measures as various kinds of torsional restraints, the IPE series profiles are arguably the best sections in terms of flexural behaviour both in terms of resistance (ULS) and deformability (SLS). Their structural efficiency under bending (ρWy) at the ULS is 7.5, that is structural performances larger than 1.5 and 2 times, respectively, those of profiles HEA and HEB.
Even more marked differences are at the SLS, with a performance referred to the strong axis (ρIy) greater than about 2 - 3 times that of homologous wide flanges double T profiles. Obviously, the activation of possible flexural-torsional buckling phenomena can significantly affect the structural efficiency of IPE profiles. In fact, in this case, it is convenient to adopt a wide flanges I profile. Among these, for equal material used, the HEA series profiles, resulting more centrifuged with respect to the two main directions, are certainly the most efficient cross-sections, they offering a structural efficiency ρIz=4.3, that is a double value compared to the corresponding IPE profile one.
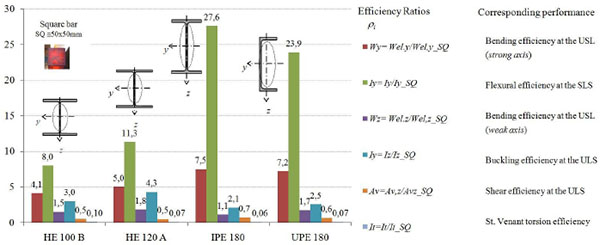
Very performing as elements under bending are also the UPE profiles, recently introduced in the European list of sections (EN 10279) [22]. These members, if compared to the homologous IPE profiles, although they have not a doubly symmetrical shape (shear-torsion coupling), show a higher centrifugation with respect to the z-z axis, which makes advisable their use in the presence of biaxial bending moment, as in the case of the purlins in inclined pitched roofs. Moreover, the presence of a straight lateral surface, without tapers essentially for technological reasons, favours their use as steel beams within staircases.
Finally, as compressed elements, the more efficient profiles are the HEB and HEM series profiles, which, together with a high centrifugation of the section with respect to the two main directions, add a significant compactness, a necessary condition to prevent insidious local instability phenomena.
CONCLUSION
In this paper, after an accurate analysis of the genesis of the hot-rolled steel I profiles, some parameters related to the profile structural efficiency, giving information about the effects that the material centrifugation generated by the lamination process induces on the structural performance of such profiles, have been provided. In particular, it has been investigated the efficiency trend of the main geometric properties related to the structural performances at the Ultimate Limit State (in terms of both resistance and instability) and at the Serviceability Limit State (in terms of deformability).
To this purpose, by analysing the narrow (IPE) and wide (HE) flanges I profiles belonging to the European list of profiles, it has been observed that the bending moment efficiencies related to the strong axis, valued in comparison to the starting semi-finished section (benchmark profile), are not constant, but they grow, as the height increases, up to 10 times in terms of resistance and 50 times in terms of deformability. Contrary, the efficiency increases over the weak axis are less pronounced, they reaching a maximum value for I profiles with height of 300mm.
The proposed methodology, applied to profiles having the same cross-sectional area (same weight and cost), has allowed to identify, under speedy way, the optimal profile for performance features and categories of use. Again with reference to the European list of sections, it has been observed under quantitative way that the IPE series profiles are, in the case of prevented flexural-torsional buckling, the most high-performance sections under bending moment. Unlike, the greater efficiency has been found in the HE profiles, with particular regard to the lightened series, when both buckling and flexural-torsional buckling phenomena are taken into account.
Finally, in addition to an internal debate, the proposed analysis approach, herein illustrated for European I sections, is quite general and, as a further development of the study, it can also be adopted to compare the different lists of sections used at the international level.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
Declared none.


