All published articles of this journal are available on ScienceDirect.
Behavior of Steel Welded Tapered Beam-column
Abstract
Steel structural elements with variable cross-section, made of welded plates, are largely used in the construction industry for both beams and columns in accordance with the stress and stiffness demand in the structure. These types of elements are mainly used for the design of single storey frames with pitched roof rafters and pinned column base. Rafters and columns can be designed as tapered members made of steel welded plates, respecting the bending moment diagrams for gravitational load combination. This paper deals with experimental tests performed on tapered beam-columns elements, subjected to both bending moment and compressive axial force together with analytical investigation.
1. INTRODUCTION
For steel industrial building, the application of elements with web-tapered I cross-section, made of welded thin plates, is a common practice. Such low rise structure elements are generally designed from gravitational load combinations. Rafters and columns shape respects the bending moment diagrams for gravitational load combination reducing the material consumption and lowering the structural self-weight. So, in case of an earthquake, low inertia forces will be provided for single span industrial buildings. This fact makes that the seismic design concept not to impose a high structural ductility class. Within the framework of an RFCS research program a simple chart based procedure to select the best seismic design concept for portal frames have been proposed [1]. Depending on the frame geometry one may propose a low-dissipative or dissipative concept. The method mentioned above indicates the fact that for most cases of portal frames with variable column and beam cross-sections, the optimal choice will be a low-dissipative concept. This concept eliminates the strict anti-seismic conditions referring to cross-section class, elements slenderness, imposed detailing conditions, etc. and conduct to a more effective cost of the building.
Due to the tapered shape of the element and from efficiency reasons, high cross-section class of web wall, i.e. 3 (elastic) and 4 (slender) may be obtained at the end with the maximum height. The buckling capacity of such a slender member will be determined by the restraining elements efficiency and position, end support conditions and initial geometrical and material imperfections.
At class 3 cross-sections members, used generally for columns elements, restrained against lateral or/and torsional buckling, the coupling between sectional capacity and overall elastic buckling of the members in compression and/or in bending may occur. In case of class 4 (slender) section members, found at the rafter highest section of the tapered web, the sectional buckling (e.g. local buckling of the walls or distortion) could appear in elastic domain.
For member which are not laterally restrained, or the restrains are not effective, the global failure mode of the members will be characterized by the lateral torsional mode, either alone or in interaction with local buckling. Nowadays, European design codes do not provide directly a practical design approach of this kind of widespread structure.
Because pitch roof portal frame rafters are subject to axial compressive loads, the problem of buckling behavior is more complex compared with the beams of multi-storey frames. Covering large volume spaces, the lateral torsional buckling capacity of the members is reduced if no restrains, or efficient restrains, are provided.
Structural stability criteria are the most important design aspect of steel buildings. The European codes series EN 1993 for design of steel structures, gives analytical and numerical procedures for buckling check. The norm provisions are generally referring at single, isolated component elements, but also gives some hints regarding the entire structures buckling capacity determination. Most code provisions cover only regular geometric shapes, simple load cases and regular boundary conditions. In case of random shapes, complicated loading cases (complex shape of internal forces diagrams) and support conditions, numerical analyses are recommended. The EN 1993 allows the use of finite element software based investigation of complex structures by using the general method. Apart from real members’ behavior (influenced by material plastic behavior, real lateral bending, torsion and warping stiffness, and second order effects, etc.), this procedure gives the possibility to take into account almost all factors concerning the buckling behavior such as geometric and material imperfections, residual stresses, actual boundary conditions.
It is obvious for all designers that the actual European norms are more detailed and complex than the previous national ones. Most of the criticism related to European norms are precisely those things. In spite of this fact, many aspects, such as elastic critical loads formulas, are left out of the current version. In the scientific literature and textbook, one may find these analytical formulas, but these are also limited to prismatic members with doubly symmetric cross-section and precise loading and boundary conditions.
Using the provisions of the general method one could attempt to design the tapered members and complex structures, but the application of this method involves advanced structural analysis (e.g. linear buckling analysis, nonlinear analysis, etc.) and skillful and well-trained engineers.
The interaction formulas for the strength and buckling check of individual elements for different type of load (e.g. tension, compression, bending, shear, torsion, and combination between them) are provided only for uniform members. Many investigations have performed on the behavior uniform elements subjected to bending moment and axial force [2-4]. Nevertheless information regarding the behavior of tapered elements is still limited.
This paper presents the results of an experimental study carried out at the Politehnica University of Timisoara, in the CEMSIG Laboratory on single tapered member subjected to bending moment and axial force. The aim of the paper is to understand the real behavior of the web tapered beam-columns member and different members and cross-sectional walls slenderness.
2. EXPERIMENTAL INVESTIGATION
The experimental specimen was isolated from a real pitched-roof portal frame designed according to the code provision and following the philosophy for single storey industrial building. Due to the testing frame geometric limitation and actuator capacity, a small-span portal frame was chosen, having 12 m span, 4 m height and roof angle of α=80 as shown in Fig. (1).
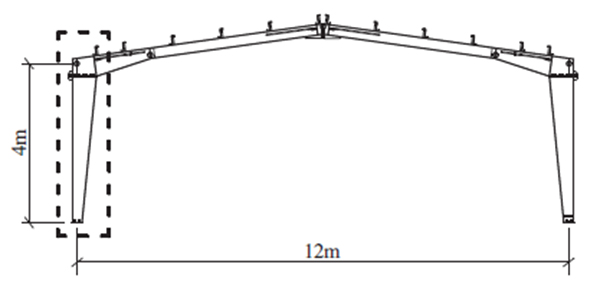
Following a low-dissipative design concept, the load hypothesis was taken according to EN1991 provisions. For the tributary area computation, a usual 6 m bay was considered. The most severe load combination for the structural design of the frame members was 1.35 P (permanent loads) + 1.5 S (snow loads), for the ultimate limit state and 1.0 P+1.0 S for the serviceability limit state, where dead load of roof cladding is P=0.35 kN/m2 and snow load is S=1.6 kN/m2. The structural elements were fabricated from S355 steel grade. The analysis method and design formulas respect the current EN 1993-1-1 provisions.
Generally, at the base the frames are pinned, if the tapered column is rationally used, using a single base plate with four bolts inside the flanges of the column. Portal frames are realized with moment resisting connections; therefore the rafter-column connection becomes rigid.
2.1. Experimental Specimens
Experimental tests were performed on steel welded columns. For different behavior cases, a number of six column cross-section geometries were used in order to model different slenderness of the column web and flanges. Their geometric dimensions and connection details are presented in Fig. (2). The overall height of the cross-sections and thickness of flanges have remained unchanged for all the experimental sets.
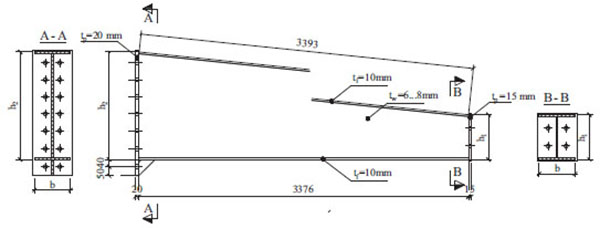
The first set of columns has a 6 mm web thickness and the second one an 8 mm web thickness, both sets are made of S355 structural steel, with flanges width of 200 mm, 180 mm and 160mm. The geometric dimensions of the specimens are presented in Table 1. Considering the building envelope disposal, the outer flange is kept vertical, whilst the inner one is inclined to give the tapered shape. At the top of the column a rigid joint was considered, thus a 20 mm thick extended end plate was provided accordingly and at the base pinned connection a 15 mm flush end plate. In order to avoid the bolt failure, 16 M20 gr. 12.9 bolts on 8 rows were used for the upper fixed connection and 4 M20 grade 8.8 on 2 rows in the case of the holding down bolts from the base connection.
| Specimen | L [mm] | h1 [mm] | h2 [mm] | b | tf | tw |
|---|---|---|---|---|---|---|
| C1_8 | 3376 | 250 | 600 | 200 | 10 | 8 |
| C2_6 | 3376 | 250 | 600 | 200 | 10 | 6 |
| C3_8 | 3376 | 250 | 600 | 160 | 10 | 8 |
| C4_6 | 3376 | 250 | 600 | 160 | 10 | 6 |
| C5_8 | 3376 | 250 | 600 | 180 | 10 | 8 |
| C6_6 | 3376 | 250 | 600 | 180 | 10 | 6 |
2.2. Material Properties
The nominal yield strength of steel plates considered for the column specimen was fy = 355 N/mm2. In order to determine the real mechanical properties of the material, tensile tests were performed on three coupons extracted from the each plate thickness used for the fabrication of the test specimens (Fig. 3).
The tensile test was carried out with UTS RSA 250kN - universal test machine. The results are presented in Table 2 only for webs and flanges material. For each specimen is indicated the resulted yield strength (fy) and ultimate yield strength (fu). The stress-strain curves prove the normal steel behavior, i.e. an elastic behavior untill yielding, followed by a small yielding plateau, a strain hardening part until necking of the specimen at the ultimate tensile strength. Although the nominal value was 355 N/mm2 (MPa), the experimental measures indicated significant differences varying the thickness of plates. The different values for the yield limit, especially for flanges may have a significant influence on the member capacity.

| Specimen | Web | Flanges | ||
|---|---|---|---|---|
| fy tw [MPa] | fu tw [MPa] | fy tf [MPa] | fu tf [MPa] | |
| C1_8 | 410 | 518 | 267 | 401 |
| C2_6 | 319 | 493 | 267 | 401 |
| C3_8 | 347 | 502 | 379 | 577 |
| C4_6 | 388 | 500 | 379 | 577 |
| C5_8 | 347 | 502 | 379 | 577 |
| C6_6 | 388 | 500 | 379 | 577 |
2.3. Test Setup and Instrumentation
The testing setup is based on a very simple static scheme. The aim of this scheme is to replicate the real loading condition on a portal frame column, i.e. members subjected to bending moment and axial force (Fig. 4). The experimental specimen, put in a horizontal position, is pinned connected at the bottom end and is rigidly connected to a very stiff and strong loading element. The additional vertical cantilever loading element has a mobile pin near the testing element and is loaded at the opposite free end with a concentrated load, introduced by a hydraulic actuator. Also, this element is lateral restrained at the top in order to avoid out-of-plane displacement due to inherent imperfections. These restrains aim at preventing the rotation of the loading element around his own axis. This fact will avoid the rotation of the specimen around his weak axis. The distance between the loading application point and the specimen centroid, i.e. the load eccentricity, represent the ratio between the value of the bending moment and axial force. Having the same length, at each new experimental test, only the column specimen was replaced.
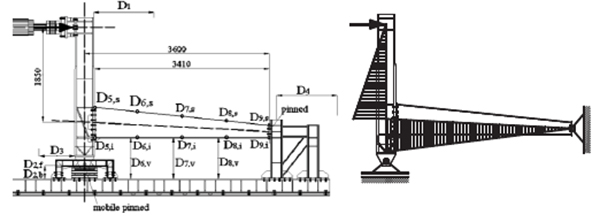
The bottom simple support was designed in such a way to allow horizontal displacement and to prevent vertical displacement both upwards and downwards. For the bending moment to be transferred directly from the vertical column to the tested specimen, it was very important for the mobile pin to work properly. For this particular reason, a roller system was provided (Fig. 5). Besides allowing free horizontal displacement, the simple support prevented the appearance of a horizontal reaction force that would lead to the change of the bending moment diagram. The tested column was considered fixed at the left end and pinned at the right end. The fixed end was made through an extended end plate bolted connection with high strength steel M20 bolts grade 12.9, while the pinned end is made through a flush end connection, with high strength steel bolts M20 grade 8.8.

The load was applied quasi-statically through a 1000 kN capacity Quiri hydraulic jack, in displacement control procedure with a displacement velocity of 3.33 mm/min. Overall view of the test setup is presented in Fig. (6). The in-plane and out-of-plane displacements were monitored during tests through a number of 18 Novotechnic displacement transducers (Fig. 4). Some of them measuring the absolute displacement of the indicated points related to points independent from the testing frame (e.g: D1,D3…D9), whilst some of the relative displacement between points located on the tested frame (e.g: D2f,b).

3. EXPERIMENTAL RESULTS
The results obtained from the experimental investigation will be summarized in the form of tables and graphs. The results recorded during the tests, in terms of load (F) and displacements (d) were converted in terms of bending moment (M) and rotation (ϕ) and finally the (M-ϕ) curve was built.
The bending moment at the top of the column (left side of the specimen) was computed using Eq. (1) whilst the rotation of the specimen at the front of the vertical element was computed using Eq. (2):
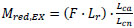 |
(1) |
Where: Mred,EX is the reduced bending moment at the column top; F is the applied horizontal force; Lr is the lever arm of the applied force, distance between point of applied force and the intersection of neutral axis of vertical column and of tapered column (Lr = 1.85m); Lcn is the nominal length of the column (3.6 m); Lca is the actual length of the column (Lca = 3.41m) (Fig. 4).
 |
(2) |
Where: ϕ is the rotation of the specimen with respect to its initial position; D1 is the measured displacement; Lr is the lever arm of the applied force (Lr = 1.85m).
The moment-rotation curves and failure modes, show the behavior of the tapered columns [6] (Figs. 1-12).
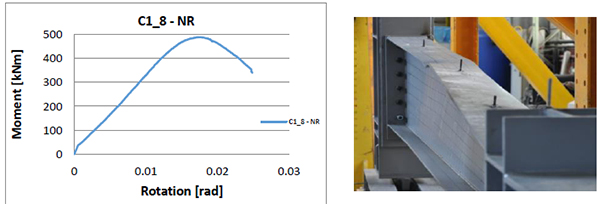
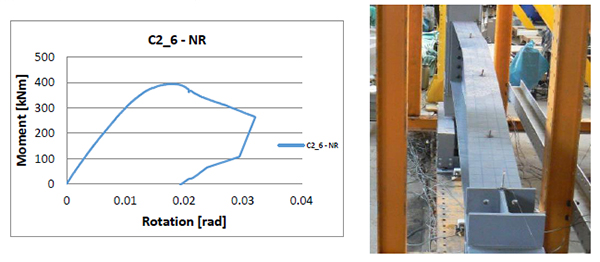
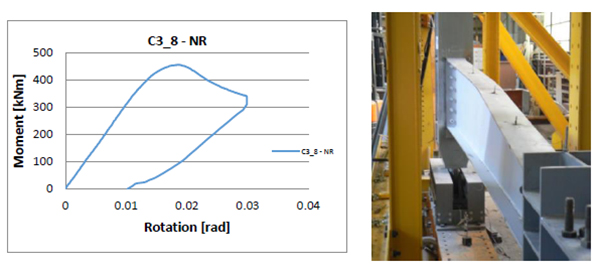
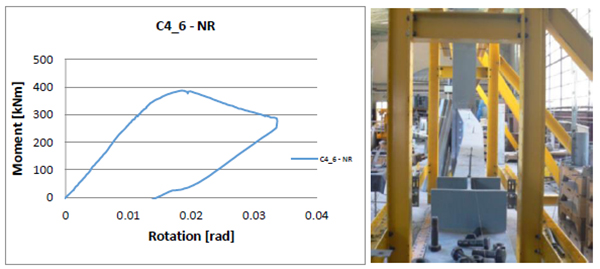
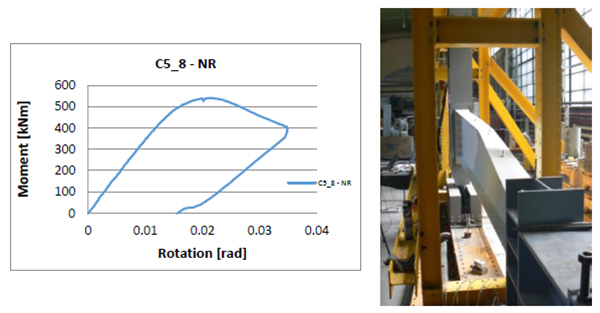
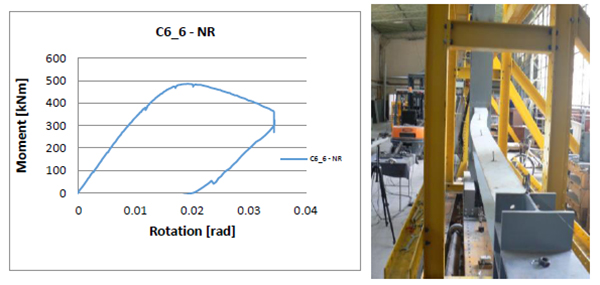
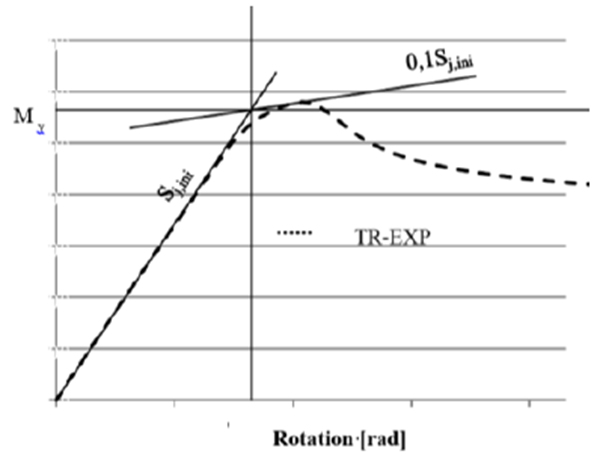
In the Table 3 are presented both the elastic (Fel) and ultimate (Fu) applied axial force, and corresponding bending moment (Mel and Mu), evaluated according to the procedure shown in Fig. (13). The elastic capacity of the experimental specimen will be considered and compared with the design capacity of the members.
| Specimen | Fel [kN] | Fu [kN] | Mel [kNm] | Mu [kNm] |
|---|---|---|---|---|
| C1_8 | 273 | 279 | 478 | 488 |
| C2_6 | 214 | 225 | 375 | 395 |
| C3_8 | 253 | 261 | 443 | 457 |
| C4_6 | 215 | 221 | 376 | 388 |
| C5_8 | 298 | 309 | 521 | 541 |
| C6_6 | 266 | 277 | 466 | 485 |
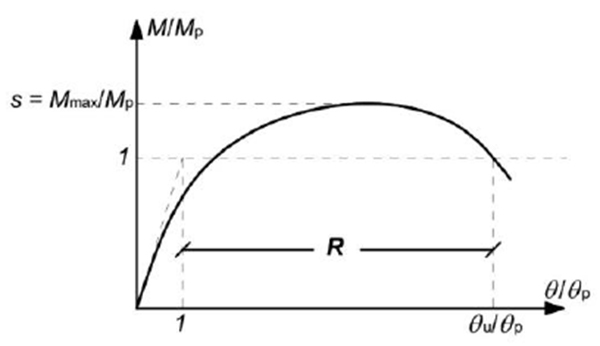
Due to the slenderness of the cross-section walls, for all specimens, the failure mode is governed by buckling phenomenon which makes the ratio between elastic and ultimate capacity (s) to vary in the range of 1.02–1.05 (Fig. 14). This fact could be also underlined by small values of the cross-section local ductility (R), expressed as a ratio between the rotation corresponding to the elastic limit and the ultimate member rotation (Fig. 14).
4. ANALYTICAL RESULTS
It is generally known that experimental tests are time, labor and money consuming. Even though, if the boundary conditions and the applied force are not provided properly, the final results of the experimental test could be significantly altered. The finite element modeling is a powerful tool as an alternative to the experimental tests for the analysis of behavior and establishing the ultimate capacity of steel structural elements, but this approach is reserved for trained and skilled engineers. Generally, methods that involve advanced numerical simulation are not preferred by design engineers.
The European norm EN 1993-1-1 describes three different procedures to verify the stability of steel elements, including beam-columns (members under combined axial load and bending). These approaches are:
An imperfection approach, by incorporating in the structural second order analysis appropriate equivalent geometric imperfections to cover the possible effects of all types of imperfections, like residual stresses and shape imperfections such as lack of verticality, lack of straightness, lack of flatness, lack of fit and the unavoidable minor eccentricities present in the joints of the unloaded structure. EN 1993-1-1 provide rules for introducing global imperfections of frames and bracing systems and local imperfections of individual members. Also, as an alternative, the shape of the relevant elastic critical buckling mode of the structure, usually the first mode, may be applied as a unique global and local imperfection.
This approach is not widely used in current design practice, but it becomes useful when advanced finite element simulations are required.
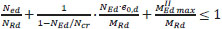 |
(3) |
The most comprehensive approach is the so-called “general method” [8]. The method no longer isolates members and separates the pure buckling modes, but considers the complex system of forces in the member and evaluates the appropriate compound buckling modes. One of the advantages of the general method is that it can examine irregular structural members such as tapered members and built-up members. Although in the current version of the Eurocode, the general method is recommended only for lateral and lateral-torsional buckling of structural components, the basic approach may be extended to other cases. Many research projects are underway across Europe intended to verify and widen its applicability.
For determining the buckling resistance of elements with non-uniform sections along the member the European norm recommends a second order analysis, accounting for imperfections or applying the general method, described in following paragraphs [9]. Overall resistance to out-of-plane buckling can be verified assuring that:
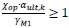 |
(4) |
Where: αult.k is the minimum load amplifier of the design loads to reach the characteristic resistance of the most critical cross-sections of the structural component, considering its in-plane behavior without taking lateral or lateral-torsional buckling into account, however, accounting for all effects due to in-plane geometrical imperfections, global and local, where relevant;
αcr,op is the minimum load amplifier for the in-plane design loads to reach the elastic critical resistance of the structural component with regard to lateral or lateral torsional buckling without accounting for in-plane flexural buckling.
χop is the reduction factor for non-dimensional slenderness 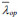 to take account of lateral and lateral-torsional buckling. The reduction factor χ may be determined from either of the following methods: the minimum (the recommended option) or an interpolated value between the values χ and χLT.
to take account of lateral and lateral-torsional buckling. The reduction factor χ may be determined from either of the following methods: the minimum (the recommended option) or an interpolated value between the values χ and χLT.
As one can notice, the general method involves advanced numerical tools and stability knowledge being very difficult to use in case of practical design application [10].
The last procedure deals with isolated members and is the conventional engineering solution for buckling problems, but its explicit code provisions are limited to uniform members with simple support and loading conditions. This method makes two simplifications considering the member isolated from the structure applying boundary conditions (supports, restraints or loads) and the buckling of the member is determinate separately for the pure buckling modes (i.e. flexural buckling for pure compression and lateral-torsional buckling for pure bending) and combined by applying interaction factors. The article will follow an analytical design procedure dealing with the stability of non-prismatic members [11]. The obtained analytic results will be compared with the experimental ones. The method is based on simple interaction formulas (see Eq. 5-7).
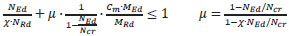 |
(5) |
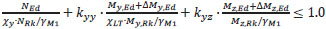 |
(6) |
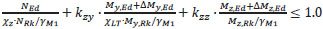 |
(7) |
In the Table 4 the main steps to assess the member buckling capacity in case of beam-columns are presented.
| Step | In the most stressed section | Isolated member |
|---|---|---|
| 1 | Calculate the design values of the compressive force and bending moment on the member | NEdMy,Rd |
| 2 | Calculate the compression and bending resistances of the cross section according with the cross section class | Nc,RkMc,Rk |
| 3 | Calculate the pure elastic critical compressive force according to minor axis flexural buckling Ncr and the pure elastic critical bending moment of the member Mcr | NcrMcr |
| 4 | Calculate the member slenderness and reduction factors separately for pure minor axis flexural buckling and pure lateral-torsional buckling (λ, χ, λLT and χLT) | 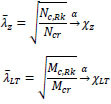 |
| 5 | Calculate the interaction factors connecting the two pure buckling cases (Annex A or Annex B) | kzy |
| 6 | Calculate the design buckling resistance of the member and check the member combination of axial load and bending | 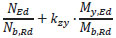 |
The elastic critical moment for lateral torsional buckling Mcr was computed, according to the method described in [11] considering an equivalent height of the element, and it was also confirmed by finite element simulations [12], i.e. buckling analysis on individual isolated members. Generally, for critical moment computation, the wrapping of the section (kw) and also the end rotation on plan (kz) are considered free. In general, this default consideration can conduct at significant underestimation of the members’ capacity. Making a more accurate estimation, according to [13] for this type of end connection (Fig. 15), both degrees of freedom can be restrained, leading to a safety factor of the element closer to the one obtained by experimental tests.
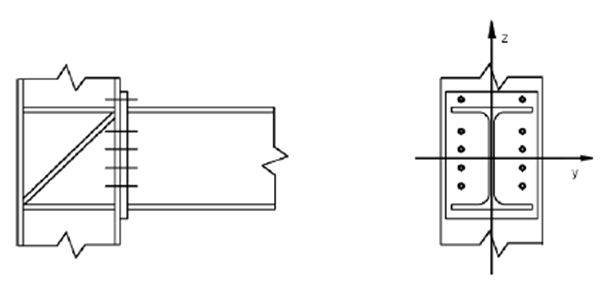
To determine the real utilization ratio of the elements, the real mechanical properties have been considered, together with the nominal value of the yielding limit. Also, a comparison between the different effective length factors kz and kw that depend on the support condition was done. The results are presented in Table 5. The design values for NEd and MEd introduced in the interaction formula verification are the capacities determined experimentally. The resulting ratio is, in fact, the underestimation ratio of the analytical calculation related to the trustful experimental results.
| End support condition | kz=kw=0.5 | kz=kw=1 | |
|---|---|---|---|
| Material properties | Determined | Nominal | |
| Specimen | Ratio* | ||
| C1_8 | 1.13 | 1.38 | 1.54 |
| C2_6 | 0.94 | 1.15 | 1.28 |
| C3_8 | 1.36 | 1.29 | 2.04 |
| C4_6 | 1.24 | 1.18 | 1.85 |
| C5_8 | 1.38 | 1.31 | 1.97 |
| C6_6 | 1.32 | 1.25 | 1.87 |
Despite using more appropriate end-condition, leading to closer values for members’ capacity, the analytical prediction gives up to 38% higher values. These differences could be explained by the members’ overstrength due to the amount of strain-hardening, defined as the non-dimensional measure of the ultimate capacity of steel members. Empirical formulation, described and discussed by means of artificial neural network formulation, predicting the rotation capacity (R) and the flexural overstrength (s) could be found in the literature [14-16].
Using a wide database of experimental results, D’Aniello et al. [14] proposed an empirical equation to predict the flexural overstrength factor (see Eq. 8). In our case, involving class 3-4 cross-sections, the overstrength factor takes values around 0.76 similar with the buckling reduction factors.
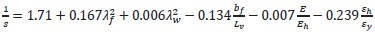 |
(8) |
Where;
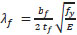 |
(9) |
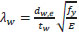 |
(10) |
Are the flange and the web slenderness parameters, respectively, with bf being the flange width, tf the flange thickness, dw,e the compressed part of the web, and tw the web thickness; Lv being the shear length, i.e., the distance between the plastic hinge and the point of zero bending moment.
CONCLUSION
Following the results showed in Table 5 one may notice an important difference between the analytical results and experimental ones in case of free end support condition, i.e. kz=kw=1. Even if these are the default values recommended being used in practical design, a careful analysis of the connection details could lead to a more rational design. The scatter in the material properties could lead to a non-conservative situation. For example, in case of C1_8 and C2_6, the flanges were manufactured using an inferior steel grade, probably S275, a situation in which a limit design process will overestimate the real element capacity.
Even if the use of restrained end condition for warping and rotation about weak axis z (kz=kw=0.5), has proven to give more accurate results, in case of inconsistencies, which often appear in practice, some situation may lead to unsafe design.
ETHICS APPROVAL AND CONSENT TO PARTICIPATE
Not applicable.
HUMAN AND ANIMAL RIGHTS
No Animals/Humans were used for studies that are base of this research.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
This work was partially supported by the strategic grant POSDRU/159/1.5/S/137070 (2014) of the Ministry of National Education, Romania, co-financed by the European Social Fund – Investing in People, within the Sectoral Operational Programme Human Resources Development 2007-2013.
The authors gratefully acknowledge the financial support of “National University Research Council – NURC-CNCSIS-Romania” through the national research grant PN-II-RU-TE-2010-1/38.


