All published articles of this journal are available on ScienceDirect.
Concentrically Braced Frames: European vs. North American Seismic Design Provisions
Abstract
A critical review of seismic design provisions for concentrically braced frames (CBFs) in both European and North American (i.e. US and Canadian) codes is presented in this paper. Indeed, even though those codes are based on capacity design philosophy, different requirements and different approaches are used to guarantee the hierarchy of resistances between dissipative and non-dissipative elements, thus leading different overall seismic performance. In detail, the main issues critically discussed are (i) the ductility classes and the correlated force-reduction factors; (ii) the structural analysis methods permitted by different codes; (iii) the modelling aspects of braces; (iv) the detailing rules for both dissipative (bracing members) and non-dissipative elements. Synoptic tables summarizing the corresponding assumptions and requirements in different codes are provided.
1. INTRODUCTION
Steel concentrically braced frames (CBFs) are widely used in high seismicity zones, owing to their structural efficiency in terms of provided lateral strength and stiffness. However, the effectiveness of seismic performance is strongly related to the adopted design provisions.
Both European and North American (US and Canadian) codes adopt capacity design principles for CBFs, which aim at guaranteeing a similar seismic performance, namely restraining the dissipative behaviour into diagonal members and preventing the damage in the remaining structural members. However, in order to achieve this purpose European and North American codes recommend some different requirements and design provisions.
Since the overall performance and energy dissipation capacity are strongly related to these detailing rules, in this paper the provisions by EN-1998 [1] (i.e. hereinafter referred as either Eurocode 8 or EC8), AISC 341 [2] and CSA S16-09 [3] are critically revised and compared for cross concentric bracings (X-CBFs) and chevron concentric bracings (Inverted V-CBFs).
It should be noted that such comparison has been done assuming the same hazard level, whose definition differs in the three examined codes. This hypothesis has been assumed in order to avoid misleading conclusions. Indeed, if one code stipulates design force larger than those given by the others, it could appear that stronger structures are designed using the former code. However, if this code allows assuming larger strength reduction factors, that conclusion cannot be valid.
In order to highlight the criticisms of the codes under consideration, hereinafter the comparative discussion has been developed focusing on the following issues:
- the ductility classes and the relevant levels of expected plastic engagement with the associated force reduction factors;
- the recommended methodologies for structural analysis and the corresponding modelling assumptions;
- the detailing rules to assure the achievement of the hierarchy of resistances for both dissipative (i.e. bracings) and non-dissipative members (i.e. beams and columns).
2. DUCTILITY CLASSES AND FORCE REDUCTION FACTORS
Seismic codes generally provide different ductility classes depending on the level of plastic engagement ensured in the dissipative zones. Therefore, a force reduction factor is assigned per each ductility class, directly related to the expected dissipative capacity. Some requirements are generally relaxed in lower ductility classes expected to provide smaller energy dissipation.
The ductility classes considered by EN-1998 [1] are the following: (i) low ductility class (DCL); (ii) medium ductility class (DCM); (iii) and high ductility class (DCH). In case of DCL poor plastic deformations are expected and the code allows performing global elastic analysis using a behaviour factor q factor within [1.5-2.0]; the strength of elements (both members and connections) is verified according to EN-1993 [4] (Eurocode 3: Design of Steel Structures) without accounting for capacity design rules (recommended just for low seismic areas). On the contrary, systems designed for DCM or DCH are expected to have moderate or large plastic engagement in dissipative parts, respectively. A specific force reduction factor is correlated at each class and the Eurocode 8 prescribes specific rules at both global and local level to assure the achievement of the expected level of ductility. In this regard, EC8 adopts the EC3 classification for cross sections relating it to the restrictions to the value of the behaviour factor q: cross-sectional class 1, 2 or 3 is required corresponding to behaviour factors in the range [1.5-2.0], while class 1 or 2 is required for q in a range [2.0-4.0]; Only class 1 is allowed for DCH (q > 4.0).
The q factor according to EN 1998-1 [1] for regular structural systems is given as follows:
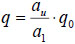 |
(1) |
Where qo is the reference value of the behaviour factor for regular structural systems, while αu/α1 is the plastic redistribution parameter accounting for the system overstrength due to redundancy. The parameter α1 is the multiplier of the horizontal seismic design action to reach the first plastic resistance in the system and αu is the multiplier of the horizontal seismic design action corresponding to the formation of a global mechanism. EC8 [1] recommends αu/α1 = 1 for CBFs.
In EN-1998 [1] a q factor equal to 4.0 in both DCM and DCH is allowed for X-CBFs, while q = 2 and q = 2.5 are used for chevron concentrically braced frames in DCM and DCH, respectively. Indeed, in Eurocode 8 the bracings in chevron configuration are expected to provide smaller energy dissipation, while it is unclear the reason why the behaviour factor for cross bracings coincides in both medium and high ductility classes. In addition, a further inconsistency can be recognized considering that EN-1998 states to assume q = 2.5 for braced frames in chevron configuration for high ductility class; indeed, according to the ductility classification given in the Section 6.1.2 of the Code, such value of the behavior factor belongs to the range [2.0, 4.0] corresponding to the DCM.
AISC 341 [2] provides two different categories based on their expected energy-dissipation capacity (i) special concentrically braced frames (SCBFs), which are expected to provide significant ductility, and (ii) ordinary concentrically braced frames (OCBFs), characterized by smaller energy dissipation capacity. OCBFs have minimal requirements compared to the other braced-frame systems; however, AISC 341 [2] significantly restricts the permitted use of OCBFs and larger seismic force must be considered to compensate for their smaller ductility. Indeed, in US codes [5, 6] the shear force reduction factor R is independent from the bracing configuration, while it depends only on the ductility class: a lower value of R factor is prescribed for OCBFs (namely equal to 3.25), while a larger value (namely equal to 6.0) is specified for SCBFs.
Also in the Canadian seismic codes (CSA S16-09 [3]), two ductility categories are accounted for as follows: (i) moderately ductile CBFs (MD), and (ii) limited-ductility CBFs (LD). In both cases, energy dissipation is obtained by means of the yielding of the brace in tension and in case of chevron bracings also of the flexural yielding at the mid-length of brace in compression after buckling. A capacity design procedure and the same design requirements apply to both classes, but some relaxations are permitted in LD Type. Similarly to US codes, the force reduction factor is independent on the brace configuration and specified as R = Rd × Ro. The factor Ro accounts for the overstrength of the structure and it is taken equal to 1.3 for CBFs, while Rd accounts for the expected ductility and it is equal to 3.0 for MD class and equal to 2.0 for LD class.
In the following sections, the design criteria and code requirements are compared especially focusing on the ductility category expected to experience the largest plastic engagement, namely: (i) EC8-compliant CBFs in DCH; (ii) AISC-compliant SCBFs; (iii) CSA-compliant CBFs in MD class.
3. STRUCTURAL ANALYSIS AND MODELLING ASPECTS
Seismic codes allow performing simplified design procedures to calculate the internal seismic forces acting on CBFs. For what concerns the design of braces, all codes allow performing a linear elastic analysis of the structure to evaluate the required strengths of the diagonal members. However, the response of concentrically braced frames is basically ruled by the behaviour of the diagonal members, which exhibit large plastic engagement after the buckling of braces; thereby the nonlinear response of the system significantly differs from the elastic behaviour. In the light of these considerations, codes provide different approaches to calculate the inner forces acting into non-dissipative members in post-buckling regime and two main methods can be recognized:
- The earthquake-induced effects in non-dissipative components (namely beams, columns and connections) are estimated magnifying by an overstrength factor Ω the internal forces calculated by means the former elastic analysis;
- A plastic mechanism analysis is used by calculating the internal forces on the basis of a free-body distribution of plastic forces transmitted by the braces yielded under tension and those under compression behaving in the post-buckling range.
In the USA, the provisions of AISC 341 [2] and the applicable building code, typically ASCE 7 [5], govern the global analysis of structures equipped with both ordinary and special concentrically braced frames. Only for SCBFs - which are expected to provide significant energy dissipation capacity- AISC 341 [2] requires, in addition to the elastic global analyses, a plastic mechanism analyses to determine the required strengths of columns, beams and connections which are thus given by considering the most unfavourable condition obtained from the following analyses:
- An elastic analysis with both braces in tension and compression resisting the design forces due to the seismic event. The obtained forces are magnified by using the system overstrength factor Ωo.
- An analysis in which all braces in tension are assumed to attain forces corresponding to their expected tensile strength, and all braces in compression are assumed to exhibit their expected post-buckling strength, representing the frame behaviour in the nonlinear range, when significant loss of compression strength and stiffness occurs.
The Canadian code also evaluates the required strength of braces by performing elastic analysis. However, differently from US codes, only plastic mechanism analysis is permitted to evaluate required strengths of beams and columns and the concept of overstrength factor to magnify the earthquake-induced forces on non-dissipative elements is absent. In order to assure the fulfilment of capacity design requirements, two different scenarios should be considered: (i) the first in which all the tension braces are assumed yielded in tension and the compression braces attain their buckling resistance (ii) the second in which all the tension braces are assumed yielded in tension and the post-buckling strength occurs in the compression ones.
Differently from the North American codes, EN-1998 [1] (except of the V-CBFs) allows performing a simplified design procedure starting from a linear analysis of the system devoted to evaluate the required strengths of bracing members and the strength hierarchy is intended guaranteed by magnifying the seismic forces given by elastic analysis acting in the non-dissipative elements by using an overstrength factor. In addition, significant difference between EC8 [1] and other codes is related to the modelling assumptions for bracing members in X-CBF configuration. Indeed, for this type of structural scheme, EC8 [1] allows performing the linear analysis on a tension-only diagonals scheme Fig. (1a), where the contribution given by the compression diagonals is neglected. This simplified assumptions needs to develop two separate models, one with the braces tilted in one direction and another with the braces tilted in the opposite direction, in order to make tension alternatively developing in all the braces at any storey. Contrarily to Eurocode 8, both US and Canadian codes mandate tension-compression bracings model (Fig. 1b) for special X-CBFs. Simplified tension-only model is allowed only for ordinary concentrically braced frames.
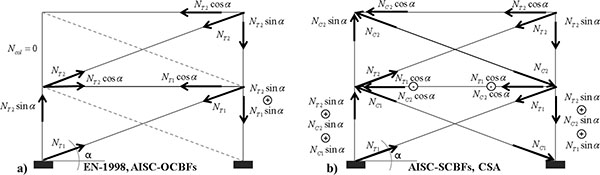
Fig. (1) depicts the force transfer mechanism obtained by using either tension only (a) or tension-compression (b) model for X-CBFs. As it can be observed, these methods lead calculating different distributions of internal forces with significant differences in terms of seismic demand on the non-dissipative members [7]. Indeed, neglecting the diagonals under compression leads to disregard force contributions in both columns and beams that could be significant (Fig. 1b).
Eurocode 8 [1] mandates plastic mechanism analyses solely to determine the design force acting on the braced-intercepted beam in chevron configuration. Indeed in this case, following the buckling of the brace in compression, an unbalanced vertical force (absent in the elastic range) resulting from the axial forces transmitted by both braces is applied on the beam, inducing a significant bending moment at the brace-intercepted section. For columns, EC8 [1] stipulates to magnify elastic forces calculated as shown in Fig. (2a). However, by comparing Fig. (2a) to (2b) it is clear that performing elastic analyses could lead to underestimate the force acting into the columns.
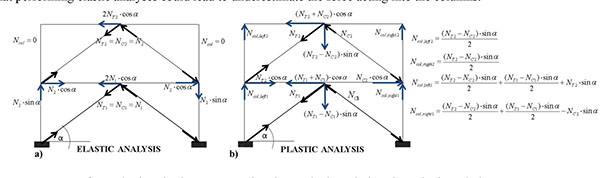
Concerning the use of overstrength factors, it is worth to note that the main philosophy is practically similar in both European and US codes; however, significant differences can be recognized in the factors definition. Indeed in US codes the overstrength factor (named Ωo) is fixed a-priori depending only on the structural typology (it is equal to 2 in SCBFs). Conversely, in EN-1998 [1] the magnification factor Ω is assumed as the minimum ratio (Npl,br,Rd,i/NEd,br,i), being Npl,br,Rd,i the plastic design strength of i-th brace and NEd,br,i its relevant required strength. As it can be easily observed the European magnification factor could be larger than 2 because it depends on the actual design overstrength of the bracing members. The main issues related to the influence of magnification factors are widely discussed in the following Sections, where the design provisions for non-dissipative members are described.
4. DESIGN OF BRACING MEMBERS
In EN-1998 [1] the diagonal members in X configuration should be designed in order to guarantee that Npl,br,Rd ≥ NEd,br, where Npl,br,Rd is the design plastic strength of brace cross-section and NEd,br is calculated as shown in Fig. (1a). On the contrary, for inverted-V CBFs, EC8 stipulates to design the braces to resist the forces calculated as shown in Fig. (2a). Thereby, compression diagonals should be designed for the compression resistance, such that χNpl,br,Rd ≥ NEd,br, where χ is the buckling reduction factor calculated according to EN 1993:1-1 6.3.1.2 (1) [4], and NEd,br is the required strength.
In addition, for both inverted V and X configurations, in order to assure an uniform distribution of damage along the building height and to avoid detrimental soft-storey mechanisms, EC8 imposes that the overstrength ratio Ωi = Npl,br,Rd,i/NEd,br,i should vary within the range Ω to 1.25Ω. It is worth to note that this requirement forces to use different cross-sections of the braces along the building height. Moreover, since the top storey is generally characterized by higher values of the overstrength ratio, the designers are forced to oversize the diagonal members at lower storeys in order to satisfy the requirement on the variation of Ω. With this regard, it may be more effective to define the i-th overstrength ratio by considering the compression axial strength of the brace at the i-th storey (rather than the plastic strength) being the buckling of the brace under compression the actual first nonlinear event occurring at each storey.
AISC 341 [2] allows tension-only bracing model just for X ordinary concentrically braced frames. Therefore, braces of special V- and X-CBFs are designed to resist both tension and compression forces evaluated by using the linear analysis (Figs. 1b and 2a). Differently from European code, in US standards, “expected” strengths are considered as design resistances for ductile elements (i.e. the capacity in tension corresponds to γovNpl,br and that in compression corresponds to γovχNpl,br), while the factored resistances are assumed in the European code.
In CSA S16-9 [3] the design of diagonal members is addressed similarly to US codes. For cross and chevron configurations both tension and compression braces are designed to withstand the earthquake-induced forces. The strength capacity of the brace in tension is calculated by using the “probable” resistance (corresponding to γovNpl,br). The compressive resistance is taken as the lesser of γovNpl,br and the brace buckling resistance (corresponding to γovχNpl,br) also evaluated using the average yield stress of the material.
It should be noted that the resistances of braces have been above defined by using the European notation also for both the US and Canadian codes, in order to allow easier comparison between the different codified rules. In particular, the European definition for the buckling capacity (namely by using the plastic strength reduced by the factor χ as defined in EN 1993:1-1 6.3.1.2 (1) [4]) has been extended to the other standards. However, slight differences in the evaluation of compression strength of braces between the examined codes can be recognized due to the different definitions of the mean buckling curve. Indeed, in the US code, the “expected” buckling strength is given as 1.14FcreAg, where Ag is the cross section area of the diagonal member and Fcre is the Eulerian critic load that is determined by using the expected yield stress RyFy (being Ry the material randomness coefficient, which corresponds to γov in Eurocode 8, and Fy is the specified minimum yield stress of the steel, which corresponds to the characteristic yield stress fy). On the other hand, in the Canadian code, the “probable” buckling resistance of bracing members is given as 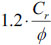 where Cr is the Eulerian critic load computed using RyFy, whose meanings are the same of the corresponding parameters given by AISC 341-10.
where Cr is the Eulerian critic load computed using RyFy, whose meanings are the same of the corresponding parameters given by AISC 341-10.
Since the braces provide poor energy dissipation in post-buckling range, the codes state further requirements devoted to limit the global and local slenderness of the bracing members.
EN-1998 [1] refers to the normalized slenderness 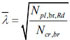 (being Ncr,br the Eulerian critical load) of bracing members, which are slightly different for X and inverted V configurations. In the former case, the brace normalized slenderness
(being Ncr,br the Eulerian critical load) of bracing members, which are slightly different for X and inverted V configurations. In the former case, the brace normalized slenderness 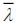 must fall in the range [1.3-2] (EN 1998-1 6.7.3(1)) [1]. This requirement is due to the simplified tension-only diagonal model assumed for structural analysis. Indeed, since the presence of the compression diagonal is neglected, the lower bound slenderness limit is imposed in order to control the maximum compression axial force transmitted to the column. On the other hand, the upper bound value is stipulated in order to avoid significant vibration and undesired buckling under service loads.
must fall in the range [1.3-2] (EN 1998-1 6.7.3(1)) [1]. This requirement is due to the simplified tension-only diagonal model assumed for structural analysis. Indeed, since the presence of the compression diagonal is neglected, the lower bound slenderness limit is imposed in order to control the maximum compression axial force transmitted to the column. On the other hand, the upper bound value is stipulated in order to avoid significant vibration and undesired buckling under service loads.
For chevron CBFs, the Eurocode 8 [1] does not impose a lower bound limit for the non-dimensional slenderness 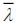 , while the upper bound limit
, while the upper bound limit 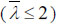 is retained. EN1998-1 [1] stipulates also local slenderness limits for cross section of braces, with reference to ductility classes.
is retained. EN1998-1 [1] stipulates also local slenderness limits for cross section of braces, with reference to ductility classes.
Differently from Eurocode 8, both US and Canadian codes refers to the geometrical slenderness KL/r (where K is the effective length factor; L is the unsupported length; r is the radius of gyration). The upper bound limit is fixed as 200 for braces in both X and inverted V configurations, thus resulting less stringent than EN-1998 [1] 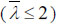 . Several studies [8-10] confirmed that frames with slender braces designed for compression strength behave well, showing also that the post-buckling cyclic fracture life increases with the slenderness. However, limiting the geometrical slenderness KL/r≤200 avoids dynamic effects in very slender braces [11]. This requirement is relaxed in AISC 341 [2] for OCBFs in V or inverted V configurations, for which
. Several studies [8-10] confirmed that frames with slender braces designed for compression strength behave well, showing also that the post-buckling cyclic fracture life increases with the slenderness. However, limiting the geometrical slenderness KL/r≤200 avoids dynamic effects in very slender braces [11]. This requirement is relaxed in AISC 341 [2] for OCBFs in V or inverted V configurations, for which
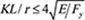 is provided, being E is Young’s modulus and Fy is the yield strength, broadly equivalent to
is provided, being E is Young’s modulus and Fy is the yield strength, broadly equivalent to 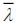 ≤1.3 for typical material properties.
≤1.3 for typical material properties.
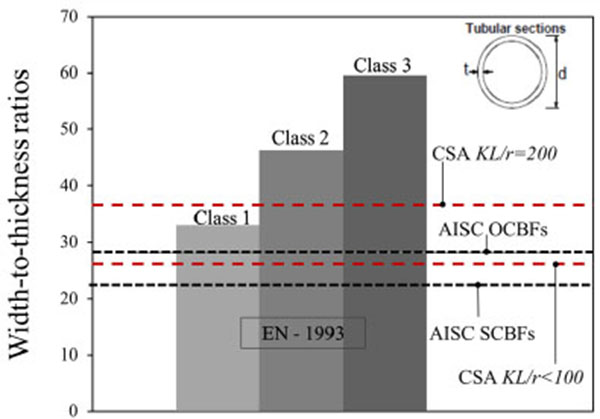
Even North American codes provide width-to-thickness ratio limitations to minimize the detrimental effects of local buckling; AISC 341 [2], for SCBFs imposes to apply specific width-to-thickness limit ratios λhd provided for members designated as highly ductile members. The requirements for OCBFs are relaxed; indeed the braces should not exceed width-to-thickness limit ratios λmd provided for moderately ductile members. With reference to local buckling phenomena, the Canadian code provides with-to-thickness ratios varying on the member slenderness: they are more strict if, while linearly increase for 100 < KL/r < 200, in the light of the above mentioned results [8-10].
In Fig. (3) the width-to-thickness ratio limitations provided by different codes are quantitatively compared for circular hollow sections (CHS) considering the same steel grade (e.g. S355); as shown in the picture, the EC8 requirements are the least severe also if compared to OCBFs, which are expected to provide very limited ductility. The most severe requirement is provided by AISC 341 [2], for SCBFs.
In Table 1 the design requirements ruling the design of diagonal members are summarized and compared for the examined seismic codes; in order to get easy the comparative reading, the nomenclature adopted by European codes was extended to all the standards under consideration.
5. DESIGN OF BEAMS
EN-1998 [1] imposes to design non-dissipative members to withstand the following force:
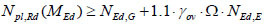 |
(2) |
where:
Npl,Rd(MEd) is the design resistance to axial force of the beam or column calculated in accordance with EN 1993:1-1 [4], taking into account the interaction with the design value of bending moment, MEd, in the seismic design situation;
NEd,G is the axial force in the beam or in the column due to the non-seismic actions included in the combination of actions for the seismic design situation;
NEd,E is the axial force in the beam or in the column due to the design seismic action;
γov is the material overstrength factor;
Ω is the minimum overstrength ratio Ωi = Npl,bRd,i/NEd,br,i;
It is interesting to observe that in most of cases the brace overstrength factors Ω for X-CBFs ranges within [1, 2], while [2, 3] for chevron CBFs, owing to the necessity to satisfy both the limits on variability of Ω and the slenderness limits for braces imposed by EC8.
In EC8, plastic mechanism analysis is required only for the braced-intercepted beams belonging to both V and inverted-V CBFs. Indeed, for those types of structural schemes, the beam behaviour significantly affects the seismic response. After brace under compression buckles, an unbalanced vertical force due to the different forces transferred by tension and compression braces is applied on the brace-intercepted beam, which is subjected to large bending moment. In such condition, the formation of a plastic hinge at mid-span of the beams should be avoided, otherwise it would result in a drop of storey lateral resistance with consequent inelastic drift concentration at the storey with yielded beam and significant deterioration of the overall response. In order to prevent this detrimental behaviour, the brace-intercepted beam should be designed to withstand: (i) all non-seismic actions without considering the intermediate support given by the diagonal members; (ii) the vertical component of the resultant force transmitted by the tension and compression braces. EN-1998 [1], calculates the vertical component acting on the brace-intercepted beam in chevron bracings assuming that the tension brace transfers a force equal to its design plastic resistance (Npl,br,Rd) and the compression brace transfers a force corresponding to reduced compression strength due to degradation under cyclic loading. The post-buckling compression strength is estimated as γpbNpl,br,Rd with a value of the factor γpb to be found in the National Annexes; the value recommended by EN 1998 [1] is equal to 0.30.
According to the AISC341 [2], the required strength for beams in SCBFs (whatever bracing configuration is selected) should be defined by considering the most detrimental condition derived from (i) performing plastic mechanism analyses or (ii) by using the system overstrength factor Ωo (fixed equal to 2) to magnify the earthquake-induced effects evaluated by mean of elastic analysis.
No overstrength factor is recommended by Canadian code [3] and only plastic mechanism analysis is permitted.
With reference to plastic mechanism analysis approach, it is interesting to note that the calculation of tension and compression post-buckling strengths of braces varies between the different codes. These differences can significantly affect the design of non-dissipative elements modifying mutual strength and stiffness ratios between the elements and thus the global performance [12-16]. According to AISC 341 [2], non-dissipative members should be designed to resist design forces derived by assuming full expected yield strength (namely γovNpl,br) for the braces in tension and the 30% of the average buckling strength for the braces in compression (namely 0.3γovχNpl,br). In CSA S16 [3], full probable yield strength (γovNpl,br) is assumed for tension brace, while the compression post-buckling strength is taken as the lesser between the 20% of the relevant probable tension strength (0.2γovNpl,br) and the buckling strength also computed using probable yield stress of the steel (γovχNpl,br).
In the light of these considerations, EC8 potentially leads to weaker beams, because it assumes the larger post-buckling strength for braces. All code requirements are compared and summarized in Table 2, where the nomenclature adopted by EN-1998 [1] is extended also to other standards.
The evaluation of post-buckling compression brace resistance (Npb) under cyclic loading represents a key aspect of seismic design of concentric bracings, because it directly affects the design of other frame members. It is worth noting that the requirement given by EN1998-1 [1] leads to assume a distribution of forces that is inconsistent when slender braces are used. Indeed, for normalized slenderness close to the Eurocode 8 upper bound limit (namely equal to 2), the brace buckling resistance tends to the 20% of the plastic strength (χ factor is about 0.2), thus resulting lower than the value (i.e. 30%) suggested by the code to evaluate the brace post-buckling strength. Moreover, several researches showed that the threshold of brace post-buckling strength is highly dependent on the brace ductility demand [16-18]. Nakashima et al. [19] showed that for braces with intermediate slenderness ratios the post-buckling resistance drops at the 20% of axial plastic strength; according to Hassan and Goel [20] the residual post-buckling strength of braces in compression has to be assumed varying from 30% to 50% of the initial compressive strength. Moreover, Lee and Buneau [21] analysed experimental data from literature in order to quantify the compression strength degradation and the actual energy dissipation experienced by bracing members under repeated cyclic loads. They recognized that the compression strength for brace with intermediate slenderness might considerably drop to approximately 20% of its original buckling strength for H-shaped bracing and 40% for square hollow section (SHS) bracing.
Thereby, from all the mentioned researches, it is clear that the post-buckling strength of braces under cyclic loading cannot univocally fixed, because it is affected by the slenderness of the member, the level of ductility demand and by the shape of the cross section.
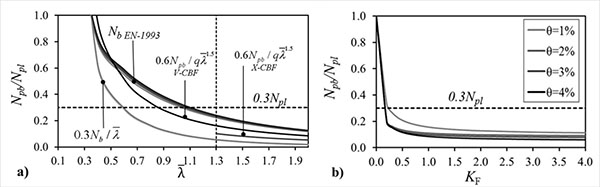
Several authors suggest alternative formulations to assess the post-buckling compressive strength: Remeninikov and Walpole [22] suggest using 0.3Nb / 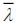 for members with
for members with 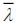 ≤0.3. Elghazouli [11] proposes to use 0.6Npb
≤0.3. Elghazouli [11] proposes to use 0.6Npb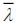 1.5 q involving as main parameters the normalized slenderness and the level of inelastic engagement given by the value of the behaviour factor q.
1.5 q involving as main parameters the normalized slenderness and the level of inelastic engagement given by the value of the behaviour factor q.
It should be noted that the braced-intercepted beams of chevron CBFs are characterized by large displacement demand at brace intersection [23, 24] and in the most of cases, it is not possible to achieve the yielding of the braces in tension, while severe ductility demand is imposed to braces under compression. With this regard, it is necessary to underline that all codified design rules and requirements focus the attention on the strength of the beam intercepting the bracing members, disregarding the role played by its flexural stiffness. Several studies [15, 25-28] already showed the influence of the beam flexural stiffness on the seismic performance of chevron bracings. Indeed, the beam displacement and the brace axial deformation are correlated phenomena, and the brace ductility demand in compression significantly increases with the beam vertical deflection. Therefore, structures with strong and deformable beams are characterized by poor seismic performance, showing severe damage concentration in the braces under compression, while those in tension behave elastically. In particular, D’Aniello et al. [15], based on an extensive parametric numerical study, provide an analytical relationship correlating the brace post-buckling compression strength to the mutual beam-to-brace vertical stiffness ratio KF. The brace post-buckling prediction curves obtained by both [22, 25] (a) and [15] (b) are shown in Fig. (4). By comparing the different formulations, it can be noted that the capacity design rule for beams given by EN 1998-1 [1] is not conservative in the most of cases, being the post buckling strength of the brace resulting from the analyses smaller than the value recommended by the code.
| Design of diagonal members | |||
|---|---|---|---|
| Requirement | EN-1998 (DCM, DCH) | AISC 341 - SCBF | CSA S16-9– MD CLASS |
| Required strength | in X-CBF: tension brace is verified for Npl,br,Rd ≥ NEd,br (tension-only bracing model is used) in V-CBF: tension brace is verified for Npl,br,Rd ≥ NEd,br; compression brace is verified χNpl,br,Rd ≥ NEd,br |
tension brace is verified for γovNpl,br≥ NEd,br compression brace is verified for min(γovNpl,br ; γovχNpl,br) ≥ NEd,br |
tension brace is verified for γovNpl,br ≥ NEd,br compression brace is verified for min(γovNpl,br ; γovχNpl,br) ≥ NEd,br |
| Check for dissipative behaviour |
Ω should vary in a range: (Ω, 1,25Ω) |
No requirement on variation of brace overstrength is imposed | |
| Limitation on slenderness | in X-CBF: in V-CBF: |
Bracing members should have: | |
| Cross-sections limitations | DCM (q>4): Class 1 or 2* DCH (2 < q ≤ 4): Class 1* |
specific width-to-thickness limit ratios λhd provided for members designated as highly ductile members are applied | with-to-thickness ratios are provided varying on the member slenderness: more strict if, while linearly increase for 100 < KL/r < 200 |
| Required strength of non-dissipative elements | |||
|---|---|---|---|
| If plastic mechanism analysis is used | |||
| Assumption | *EN-1998 (DCM, DCH) | AISC 341 (SCBF) | CSA S16-09 (MD CLASS) |
| Force in tension braces | Npl,br,Rd | γovNpl,br | γovNpl,br |
| Force in compression braces | 0.3Npl,br,Rd | 0.3χγovNpl,br | min(0.2γovNpl,br; γovχNpl,br) |
| If overstrength factor is used | |||
| Assumption | EN-1998 (DCM, DCH) | AISC 341 - SCBF | CSA S16-09 MD CLASS |
| Overstrength factor | 1.1 γovΩi i | Ω=2 | - |
Another key aspect is related to the beam-to-column connections in the braced bays. Indeed, AISC 341 [2] requires moment-resisting beam-to-column connections in the braced bays in order to improve the degree of redundancy and thus favoring redistribution of damage. In addition, this requirement also allows increasing the beams flexural stiffness, thus resulting in better performance [15, 25-28]. No similar requirement can be recognized in European and Canadian codes.
6. DESIGN OF COLUMNS
EN-1998 [1] imposes to design the columns of the braced bays, independently from bracing configuration, to withstand the force given from Eq. (2); no plastic mechanism analysis is requested to evaluate the required strength of columns [29]. According to the US approach, similarly to the requirements for beams, the required strength of columns in SCBFs is defined by considering the most severe condition among the forces obtained magnifying by the system overstrength factor Ωo = 2 or those obtained by plastic mechanism analysis (as described in Sections 3 and 5).
Similarly to the beams, CSA S16 [3] does not provide any overstrength factor and the strength hierarchy is assured only by means of plastic mechanism analysis. With this purpose, two loading conditions occurring in the compression braces should be considered in conjunction with tension braces developing their probable yielding strength: (i) the compression acting braces attaining their probable compressive strength (ii) the compression acting braces attaining their probable buckled resistance.
Moreover, the Canadian code [3] includes additional provisions to account for the flexural demand imposed on continuous columns of multi-storey structures deriving from the variation in storey drifts between adjacent storeys in seismic event. Since this bending moment is usually disregarded by performing linear elastic analysis, CSA S16 [3] states that columns of braced bays should be designed considering an additional bending moment equal to the 20% of their plastic flexural strength. No similar requirement is given by other codes (Table 2).
CONCLUSION
The current paper provided a critical overview on seismic design provisions for concentrically braced frames given by European and North American standards. On the basis of the main issues discussed in the manuscript, the following remarks can be drawn:
- The behaviour factor given by US and Canadian codes does not depend on the bracing configuration. This implies that both X-CBFs and Chevron CBFs can be designed with the same design base shear force. On the contrary, Eurocode 8 recommends different behaviour factors for different bracing configurations, namely larger for cross CBFs (e.g. q = 4) than those for chevron CBFs (e.g. q = 2.5), because the former are expected to provide the larger ductility.
- AISC 341 [2] allows using the largest behaviour factor (i.e. q = 6), thus leading to braces more slender than those obtained according to EC8 [1].
- EC8 [1] generally allows using simplified design procedures; indeed, in the most of cases is sufficient to perform only a linear elastic analyses without calculating the plastic distribution of forces occurring after the brace buckling [29]. On the contrary, both US and Canadian codes stipulate to perform further plastic mechanism analyses in order to assure the fulfilment of capacity design criteria. Even though the European approach involves a significant simplification of design process, it often leads to underestimate the earthquake-induced effects in the non-dissipative members, leading to non-conservative design in the most of cases. This aspect is more evident for the columns in X-CBF configuration and for the beams in chevron configuration.
- With reference to the design of dissipative bracings, the requirements devoted to limit both global and local slenderness mighty differ between the examined codes. The requirements on global slenderness of the members are more relaxed in North American codes respect to EN-1998, being based on the evidence that the post-buckling cyclic fracture life increases with an increase in geometrical slenderness. Moreover, by quantitatively comparing the width-to-thickness ratio (namely local slenderness) limitations, it emerged that US code provides the most severe limits. Conversely, EC8 limitations also for higher ductility classes are less severe even than US requirements for OCBFs, which are expected to provide the smallest ductility.
- With reference to the evaluation of post-buckling force acting in the diagonal members after the buckling of the compression bracings, it is not possible to recognize a unified approach between different codes. All examined codes do not relate the brace post-buckling strength either the brace slenderness or the level of plastic engagement, which instead significantly affect the degradation of brace compressive strength under repeated cyclic loading. In addition, if compared with more recent data from literature, the thresholds for post-buckling strengths suggested by the codes seem to be not conservative in the most of cases.
- Design provisions for chevron concentrically braced frames need to focus also on the stiffness of the brace-intercepted beam, being the beam deflection and the braces ductility demand correlated phenomena.
- Only US code provides further requirement relating to the beam-to-column connections in the braced bays, which should be moment-resisting type, in order to improve the redundancy of the system and thus favoring redistribution of damage. No similar requirement can be recognized in European and Canadian codes.
- Further research is needed in order to better quantify the differences in terms of provided seismic performance for CBFs designed according to either European or North American codes.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
Declared none.


