All published articles of this journal are available on ScienceDirect.
Assessment of the Design Criteria for Concentric V-Braced Steel Structures According to Italian and European Codes
Abstract
The critical review of design methodologies provided by the NTC2008, in agreement with the European seismic code (Eurocode 8) for steel Concentrically Braced Frames with chevron (or inverted V) diagonals (CBF-V), carried out by deepening the seismic behaviour of such typical steel seismic resistant structures, aims to provide more efficient design criteria able to ensure adequate safety levels under seism.
As reference case studies, common structural configurations of CBF-V are designed according to the NTC2008 provisions. Each case study is designed through both the Linear Static (LS) and Dynamic (LD) analysis. For braces either Circular Hollow Sections (CHS) or HE profiles are used. General critical issues have been evidenced in the design process. The seismic performance of investigated structures is evaluated by non-linear static analyses, in order to appraise the most relevant behavioural issues, like the behaviour factor, the failure modes and the effectiveness of the capacity design criteria. A discussion on the obtained results has allowed to point out the pros and cons of the current design approach.
1. INTRODUCTION: DESIGN CRITERIA FOR CBF-V STRUCTURES ACCORDING TO NTC2008-EC8
In principle, Concentrically Braced Frames (CBF) should resist the seismic actions thanks to the contribution of both tensile and compression braces. For dissipative systems, braces are designated as the dissipative elements. At the ultimate limit state the ideal condition is the simultaneous buckling of the braces in compression and yielding of the braces in tension, while beams and columns should remain in elastic range; therefore, they should have an adequate over-strength with respect to braces, for this purpose the capacity design criterion, through the use of the overstrength factor Ω, is applied [1] (Table 1).
At present, the Italian design rules for constructions are provided by the NTC2008 [2, 3], based on the European seismic code (Eurocode 8) [4]. A general overview of the design aspects and applications related to steel CBF-V structures, among the other typical steel seismic resistant structures, is presented in Mazzolani et al. [5, 6], where the modern approach is discussed, evidencing the conformity between the Italian and European codes. A more rigorous plastic design procedure for CBFs was proposed by Longo et al. [7, 8], more recently Marino has proposed a unified design approach for concentric bracing systems [9]. A wide research activity, aiming at the progressively upgrading and optimization of seismic design criteria for all types of construction, including steel braced structures, is ongoing within the Italian project RELUIS-DPC. In this context, recently a deep analysis of X braced structures has been already presented by Faggiano et al. [1].
In Table 1 the NTC2008-EC8 Ultimate Limit State (ULS) design rules for seismic resistant systems with inverted V (CBF-V) braces are summarized [10, 11].
In the CBF-V system, the compressed brace provides a contribution to the overall system stability, thus it cannot be neglected. For this reason, both braces are taken into account in the design model. Therefore, the design resistance is the buckling strength (Eq.1) and only the upper limit of the normalized slenderness of diagonals is imposed (Eq. 2), aiming at avoiding excessive distortions of braces in compression due to buckling, which could cause permanent damage to either connections or not structural claddings. The over-strength factor Ω, used for the design of beams and columns according to the capacity design criterion, has to be uniform in elevation, according to the well-known limitation given in Eq. 3. In addition, beams have to be designed by considering the concentrated force at the middle-span due to the unbalanced force between the plastic resistance of the tensile brace and the residual resistance of the compressed one after buckling, the latter being set equal to 30% of the brace plastic resistance (Eq. 4). The beam is therefore subjected to bending moment, shear and axial load.
The behaviour factor is equal to 2.5 and 2 for High and Low ductility classes, respectively. Of course, members should be ductile, thus belonging to Class sections 1 or 2, according to the cross section classification defined in Eurocode 3 [12, 13] and taken by NTC2008.
| Bracing | Class sections 1 or 2; for circular hollow sections: d/t ≤ 36 | ||
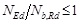 |
|||
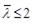 |
|||
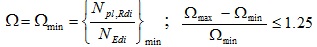 |
|||
| Beam | 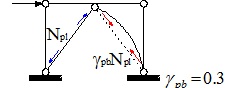 |
||
| Column | 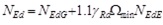 |
||
| q-factor | Ductility Class | High | 2.5 |
| Low | 2 | ||
where: d and t are diameter and thickness of the circular hollow profile, respectively; NEd is the brace design axial force; Npl,Rd is the brace plastic resistance; Nb,Rd is the brace buckling resistance;
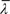 is the brace normalized slenderness; Ω is the over-strength factor; γRd is the steel over-strength factor that is the ratio between the average and the characteristic values of the yielding strength; γpb is a factor representative of the residual brace strength after buckling; NEdG is the axial force corresponding to non-seismic loads and NEdE is the axial force corresponding to seismic loads. is the brace normalized slenderness; Ω is the over-strength factor; γRd is the steel over-strength factor that is the ratio between the average and the characteristic values of the yielding strength; γpb is a factor representative of the residual brace strength after buckling; NEdG is the axial force corresponding to non-seismic loads and NEdE is the axial force corresponding to seismic loads. |
|||
2. THE CASE STUDY
The study structures have typical configuration and geometrical dimensions. They belong to a regular building, with 3, 6 and 10 floors, the interstorey height is h = 3.5m (at the ground floor hGF = 4m) and the span L = 6m. The reference geometrical scheme is shown in Fig. (1). The structures are designed for high ductility class and they are assumed to be located in a high seismicity zone (ag = 0.35g) on a category B soil. For the sake of simplicity, the elastic spectrum is obtained according to the code OPCM 3431 [14] since seismic parameters are independent from the geographic position, unlike the current NTC2008. Each case study is designed through either the Linear Static (LS) or Linear Dynamic (LD) analyses. As far as the selection of the member profiles is concerned, for columns two cross section types are used, namely welded box sections and hot-rolled wide flange (HE) profiles, for beams hot-rolled wide flange (HE) profiles are used; while for braces two cross-section types, namely Circular Hollow Sections (CHS) and wide flange (HE) profiles, are used, as indicated in Fig. (1).
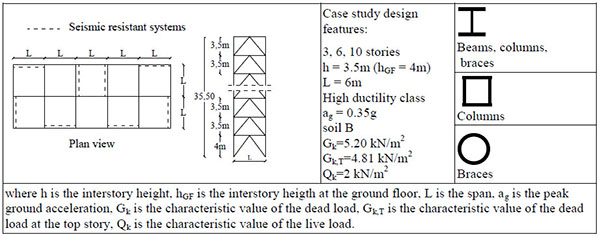
Dead and permanent loads, uniformly distributed on the floors, are assumed as Gk=5.20 kN/m2 for standard intermediate floors and Gk,T=4.81 kN/m2 for the roof floor. Live loads, corresponding to residential buildings, are assumed as Qk=2 kN/m2 for both intermediate and roof floors. The structures are designed according to the NTC2008-EC8 design approach, giving rise to a total number of 12 case studies. As far as the Damage Limit State (DLS) is concerned, the limitation of the inter-story drift equal to 1% is considered. The main design features are also reported in Fig. (1).
The results of the design phases in terms of member profiles of the different investigated structures together with the total weight of each member type are provided in Tables 2-4, for 3, 6, 10 stories frames respectively, in both cases, the diagonals are made by CHS or HE profile types.
| Diagonal CHS | ||||||
|---|---|---|---|---|---|---|
| Storey | LS | LD | ||||
| Diagonal | Column | Beam | Diagonal | Column | Beam | |
| (CHS) | (HE) | (HE) | (CHS) | (HE) | (HE) | |
| 3 | 139,7x4 | HE240B | HE280B | 139,7x5 | HE260B | HE300B |
| 2 | 168,3x5 | HE240B | HE320B | 168,3x6 | HE260B | HE360B |
| 1 | 177,8x6,3 | HE240B | HE400B | 168,3x8 | HE260B | HE450B |
| Member weight [kN] | 6 | 18 | 23 | 7 | 20 | 25 |
| Diagonal HE | ||||||
| Storey | LS | LD | ||||
| Diagonal | Column | Beam | Diagonal | Column | Beam | |
| (HE) | (HE) | (HE) | (HE) | (HE) | (HE) | |
| 3 | HE140A | HE280B | HE360B | HE160A | HE300B | HE400B |
| 2 | HE180A | HE280B | HE450B | HE200A | HE300B | HE500B |
| 1 | HE220A | HE280B | HE550B | HE240A | HE300B | HE650B |
| Member weight [kN] | 10 | 22 | 30 | 13 | 25 | 33 |
| Diagonal CHS | ||||||
|---|---|---|---|---|---|---|
| Storey | LS | LD | ||||
| Diagonal | Column | Beam | Diagonal | Column | Beam | |
| (CHS) | (HE) | (HE) | (CHS) | (HE) | (HE) | |
| 6 | 139,7x5 | HE320B | HE300B | 139,7x5 | HE260A | HE300B |
| 5 | 168,3x6,3 | HE320B | HE360B | 168,3x6 | HE260A | HE360B |
| 4 | 193,7x8 | HE360B | HE450B | 168,3x8 | HE300B | HE450B |
| 3 | 177,8x10 | HE360B | HE500B | 168,3x10 | HE300B | HE450B |
| 2 | 219,1x10 | HE400M | HE550B | 168,3x10 | HE340M | HE450B |
| 1 | 244,5x10 | HE400M | HE600B | 177,8x12 | HE340M | HE550B |
| Member weight [kN] | 21 | 77 | 61 | 18 | 64 | 57 |
| Diagonal HE | ||||||
| Storey | LS | LD | ||||
| Diagonal | Column | Beam | Diagonal | Column | Beam | |
| (HE) | (BOX) | (HE) | (HE) | (BOX) | (HE) | |
| 6 | HE160A | 400x15 | HE400B | HE160A | 400x15 | HE400B |
| 5 | HE220A | 400x15 | HE550B | HE200A | 400x15 | HE500B |
| 4 | HE260A | 400x15 | HE650B | HE240A | 400x15 | HE600B |
| 3 | HE240B | 400x15 | HE800B | HE260A | 400x15 | HE650B |
| 2 | HE260B | 400x35 | HE800B | HE260A | 400x30 | HE650B |
| 1 | HE280B | 400x35 | HE900B | HE320A | 400x30 | HE900B |
| Member weight [kN] | 40 | 113 | 82 | 34 | 105 | 76 |
| Diagonal CHS | ||||||
| Storey | LS | LD | ||||
| Diagonal | Column | Beam | Diagonal | Column | Beam | |
| (CHS) | (BOX) | (HE) | (CHS) | (BOX) | (HE) | |
| 10 | 139,7x4 | 440x15 | HE360B | 139,7x4 | 400x15 | HE320B |
| 9 | 139,7x8 | 440x15 | HE360B | 139,7x6 | 400x15 | HE320B |
| 8 | 168,3x8 | 440x20 | HE550B | 168,3x6 | 400x15 | HE400B |
| 7 | 168,3x12,5 | 440x20 | HE550B | 168,3x8 | 400x15 | HE400B |
| 6 | 168,3x12,5 | 440x25 | HE600B | 168,3x8 | 400x20 | HE500B |
| 5 | 193,7x12,5 | 440x25 | HE600B | 168,3x10 | 400x20 | HE500B |
| 4 | 219,1x12,5 | 440x30 | HE650B | 168,3x10 | 400x25 | HE500B |
| 3 | 219,1x12,5 | 440x30 | HE650B | 219,1x8 | 400x25 | HE500B |
| 2 | 273x10 | 440x40 | HE800B | 193,7x10 | 400x30 | HE550B |
| 1 | 273x12 | 440x40 | HE800B | 219,1x10 | 400x30 | HE550B |
| Member weight [kN] | 45 | 240 | 122 | 31 | 178 | 101 |
| Diagonal HE | ||||||
| Storey | LS | LD | ||||
| Diagonal | Column | Beam | Diagonal | Column | Beam | |
| (HE) | (BOX) | (HE) | (HE) | (BOX) | (HE) | |
| 10 | HE140A | 700x20 | HE320M | HE160A | 650x20 | HE500B |
| 9 | HE200A | 700x20 | HE320M | HE200A | 650x20 | HE500B |
| 8 | HE240A | 700x20 | HE550M | HE240A | 650x20 | HE650B |
| 7 | HE220B | 700x20 | HE550M | HE260A | 650x20 | HE650B |
| 6 | HE260B | 800x25 | HE700M | HE240B | 650x25 | HE800B |
| 5 | HE320A | 800x25 | HE700M | HE260B | 650x25 | HE800B |
| 4 | HE340A | 800x30 | HE900M | HE260B | 650x30 | HE900B |
| 3 | HE300B | 800x30 | HE900M | HE280B | 650x30 | HE900B |
| 2 | HE360A | 800x40 | 950x300 x60x20* | HE280B | 650x40 | HE900M |
| 1 | HE400B | 800x40 | 950x400 x60x20* |
HE400A | 650x40 | HE900M |
| Member weight [kN] | 81 | 450 | 191 | 73 | 376 | 153 |
3. DESIGN ASSESSMENT OF CBF-V
Commonly, the design of columns is conditioned by the gradual cross-section reduction criterion. In fact, strong variation of the cross-section sizes along the building height should be avoided, they being generally a source of localised damage. Moreover, the structure story stiffness variation at consecutive floors should be limited, in order to fulfill regularity requirements devoted to assure the achievement of the most uniform state of stress and deformation and in particular plastic hinges distribution along the structure height at the ultimate limit states. Another influencing design aspect is that HE profiles larger than HEB300 are barely able to withstand high axial loads, because, as far as the depth increases, the base is almost constant; thereby, being the increment of second moment of area extremely limited, for profiles larger than HEB300, the axial buckling check is hard to be satisfied. For these reasons, for 10 stories structures and 6 stories HE braces structures, the columns are realized with square box sections built-up by welding, having cross-section opportunely reduced along the building height, in order to absorb the high axial loads deriving from the capacity design criterion. The choice of box sections is dictated by the criterion of maximum structural exploitation with minimum weight, compared to other solutions, such as Austrian cross and welded I sections. Columns are HE profiles for 6-storey frames in case of CHS braces, as the same for 3-story frames, where, due to the limited number of floors, the hierarchy design criterion is not penalising.
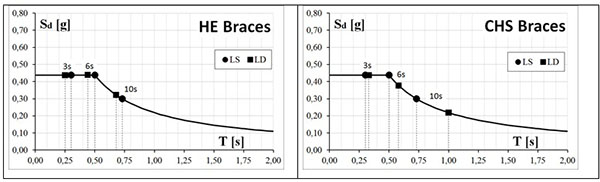
In Table 5 the main design information on the study structures, such as first vibration period T1, base shear Fh, weight W and design over-strength factor Ωmin, are reported. In Fig. (2) the response spectra with the evidence of T1 for 3, 6 and 10 storeys structures (3s, 6s, 10s) in case of HE braces and CHS braces are shown.
| Design Method | N. storeys | W [kN] | T [s] | Fh [kN] | Ωmin | ||||
|---|---|---|---|---|---|---|---|---|---|
| CHS | HE | CHS | HE | CHS | HE | CHS | HE | ||
| LS | 3 | 46 | 63 | 0.3* | 0.3* | 549 | 549 | 2.15 | 3.90 |
| 6 | 159 | 234 | 0.5* | 0.5* | 1085 | 1085 | 2.11 | 4.04 | |
| 10 | 408 | 722 | 0.73* | 0.73* | 1254 | 1254 | 2.46 | 4.43 | |
| LD | 3 | 52 | 71 | 0.33 | 0.25 | 580 | 588 | 2.32 | 4.21 |
| 6 | 140 | 215 | 0.58 | 0.44 | 1062 | 1064 | 1.86 | 3.41 | |
| 10 | 309 | 602 | 1 | 0.68 | 988 | 1428 | 2.34 | 3.70 | |
| *T=C1H3/4 with C1 = 0.05, H= total height of the structure | |||||||||
In general, some observations can be done by comparing on one hand, CHS and HE braces structures, on the other hand, LS and LD design.
CHS braces structures are lighter than HE braces structures. This is particularly evident for LS 10s buildings, where the adoption of HE braces induces the use of welded double T beam profiles at the lower storeys, due to the high forces transferred by the braces, oversized for the limited availability of standard HE hot-rolled profiles. This limitation does not exist for CHS profiles, which are produced with a large range of cross-sections.
The vibration periods T1 determined by LD analysis are higher for HE braces structures than for CHS braces structures, in conformity to the previous observation. In the LS design, the first vibration period does not depend on the bracing details, it being calculated by means of the simplified formula. Moreover, the LD T1, with respect to the LS T1 is lower for HE braces structures, is higher for CHS braces structures.
In case of 10s and 6s structures the LD design gives rise to lower base shears and weights as respect to the LS design, contrary in case of 3s frames. This trend does not reflect the variation of the first periods of vibration T1, due to the influence of the superior modes of vibration, which could not provide negligible additional actions that are ignored by the LS analysis.
Concerning the over-strength factor these are the following observations:
- High values of Ωmin, ranging from 1.86 to 2.46 and 3.41 to 4.43 for CHS and HE braces structures, respectively, are achieved. These imply a significant increment of design axial forces in the columns according to the capacity design.
- The Ω variation ratio (Eq. 3) is always governed by the top storey braces, whose Ω values are generally larger than those at lower storeys. This is due to the use of brace cross-sections, which are subjected to low seismic actions but should contemporary respect the standard slenderness limit. As a consequence, elastic members are oversized, it producing a weight increase.
- In case of HE braces, Ωmin is generally larger than the design behaviour factor q (2.5), what is not acceptable.
Based on the previous observations possible improvements of the design criteria for CBF-V can be related to the following items:
- The use of HE profiles for structural members can become more convenient if a wider spectra of cross sections are produced, in order that profiles could best fit all the design requirements in terms of strength and stiffness, reducing the overstrength that alters the effect of the design provisions as respect to the expectations. This could also either avoid the scatter in the geometrical variability of members composed by different parts, as it occurs for columns belonging to high rise buildings, or enhance the efficiency of the capacity design, or simplify the connection among members.
- The simplified formula for the determination of the first period of vibration, necessary in case of LS design, should be better fitted according to the number of floors, taking also into account the structural system type, being differentiated in case of bracing systems and for type of bracings.
- The top story needs specific design criteria, which balance capacity design and slenderness requirements. To this concern, some authors proposed the reduction of the bracing members section at the ends to obtain Ω=1 [15, 16].
- With regards to capacity design, it should be explicitly stated that the overstrength factor Ω should be in any case lower than the design behaviour factor q.
It is worth noticing that items 1 and 4 could be valuable for any type of structural system, not only for CBF-V.
4. NUMERICAL MODELING
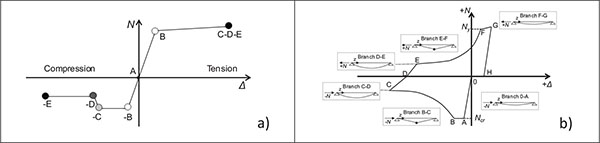
Structural analyses are performed by means of the FEM software SAP2000 v. 14.0.0 [17]. Members are modeled as beam elements with lumped plasticity, columns are continuous along the total height and both beam-to-column and brace-to-beam connections are hinged. Plastic hinges of beams and columns are modelled by considering the classic elastic-perfectly plastic constitutive law [18]. For bracing members, the force-displacement model shown in Fig. (3a) is assumed. It is a simplification of the mathematical model proposed by Georgescu [19], which is depicted in Fig. (3b). The brace ductility is limited according to the simplified approach proposed by Tremblay [20]. In this way, it is possible to take into account, although with approximation, the actual behaviour of braces in compression [21-23], consisting in the buckling and then post-buckling phases, where a loss of strength and stiffness results in a reduction of the brace dissipative capacity.
Details about the modeling assumptions are given in Faggiano et al. [1].
5. BEHAVIOUR FACTOR EVALUATION
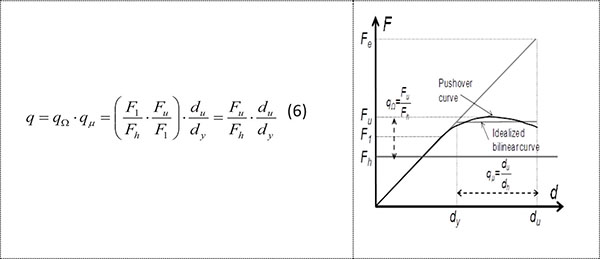
The behaviour factor q is defined through Eq. (6) given in Fig. (4) [24], where qΩ and qμ are the behaviour factor contributions related to over-strength and ductility, respectively; F1 is the base shear at the first non-linear event, Fh is the design base shear, Fu is the maximum base shear value on the pushover curve, dy is the displacement corresponding to the conventional elastic limit and du is the ultimate displacement. Details about the q-factor definition are given by Faggiano et al. [1].
In this work, the behaviour factor q is calculated according to the following assumed ultimate displacement du: the lowest displacement among the ones due to the development of a collapse mechanism, to the achievement of the diagonal maximum local ductility of the brace or to the 15% strength loss with respect to the peak force on the pushover curve. It is worth noticing that the du at the achievement of the inter-storey drift equal to 2% is provided by FEMA 356 for braced steel structures at Collapse Prevention limit state [25].
6. SEISMIC PERFORMANCE EVALUATION
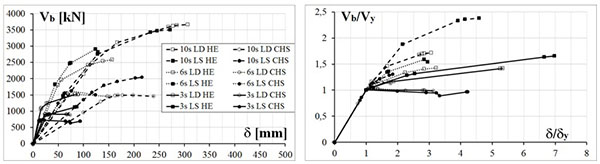
The seismic performance of the study structures is evaluated in terms of failure modes and behaviour factors by means of non-linear static (pushover) analyses. In Fig. (5), pushover curves are represented both in the base shear (Vb) vs top displacement (δ) plane (Fig. 5a) and in the Vb/Vy vs δ/δy normalised plane, Vy and δy being respectively the shear related to the first plastic hinge and the corresponding displacement (Fig. 5b), where the Vb/Vy can be intended as an over-strength coefficient.
It can be noticed that generally the LS structures have Vb/Vy ratios greater than the LD structures.
CBF with HE braces have always increasing curves; if compared to CBFs with CHS braces, they exhibit greater stiffness and larger ultimate displacements (Fig. 5a). Moreover, the CHS structures strength reserve after the first non-linear event is smaller, since they attain suddenly the ultimate resistance (Fig. 5b).
In Fig. (6) the failure modes for the investigated CBF-V are depicted. In all cases, the collapse of structures occurs because of a beam mechanism located at the top storeys with the formation of plastic hinges in the beams. Generally, this condition leads towards a limited number of buckled braces for taller structures while the tension braces behave elastically leading to poor energy dissipation.
The generalized exhibited beam failure mechanisms are indicative of the low dissipative capacity of NTC08 CBF-V. This behaviour can be ascribed to the design criterion, which assumes γpb=0.3 for the calculation of the unbalanced vertical force applied to the beam Table 1. In fact, according to the buckling curves b and c typical of the used bracing profiles (Fig. 7), the reduction factor χ for bracings with normalized slenderness close to the upper limit given in Eq. 4 results to be equal to about 0.2.

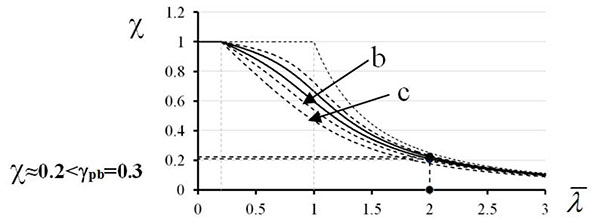
This value is smaller than the post-buckling residual strength (γpb=0.3) proposed by the code. In addition, for the investigated cases, the Georgescu model [19] provides, at the maximum local ductility predicted by Tremblay [20], a strength reduction of Npl up to 6-7%. Therefore, the assumption γpb=0.3 is not conservative.
Another key aspect responsible for the poor overall response of chevron CBFs has been recently evidenced in literature, being related to the beam flexural stiffness [26, 27].
For 3s frames, the behaviour factor for the CHS brace structures is greater than 2.5, for 6s and 10s frames, the behaviour factor is about 2.5. Nevertheless, in all investigated cases, structures with HE braces always have behaviour factor largely greater than 2.5 (Table 6 and Fig. 8). This result can be ascribed to the lower over-strength of structures with CHS braces.
| CHS LD | CHS LS | HE LD | HE LS | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N. storeys | qμ | qΩ | q | qμ | qΩ | q | qμ | qΩ | q | qμ | qΩ | q |
| 3 | 1.53 | 2.16 | 3.31 | 1.31 | 2.24 | 2.94 | 1.82 | 3.85 | 7.01 | 1.25 | 4.90 | 6.13 |
| 6 | 1.39 | 1.89 | 2.62 | 1.42 | 1.80 | 2.55 | 1.70 | 3.13 | 5.32 | 1.69 | 2.80 | 4.73 |
| 10 | 1.56 | 1.51 | 2.35 | 1.52 | 1.64 | 2.49 | 1.95 | 2.57 | 5.00 | 1.76 | 2.76 | 4.86 |
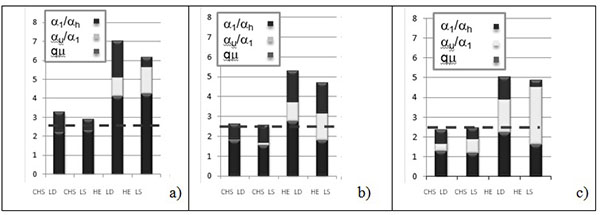
Moreover, in almost all cases, the collapse condition corresponds to the attainment of the local ductility limit of braces, whereas only in few cases, the value of the inter-storey drift reaches 2%.
Based on the previous observations, it is apparent that the current design criteria lead to structures that behave all in all as expected and even better than previsions, in terms of ductility and dissipative capability, as testified by the comparison between the design and calculated behaviour factors, although the ideal collapse condition is not attained, being characterized by a local beam mechanism at the top story, in absence of brace plastic behaviour in tension. This issue underlines that the capability of the CB-V structural systems is not exploited, requiring a large improvements of the design criteria for enhancing the seismic structural behaviour. In particular, a more appropriate reduction factor γpb for the determination of the residual strength of buckling braces should be assumed.
CONCLUSION
The current technical rules for the design of V braced seismic resistant structures according to the Italian technical code for constructions (NTC 2008), which is aligned to the EC8, appear to be poorly efficient in catching the actual structural capability of the CB-V systems. The case of V braces is peculiar for the beam design, due to the convergence of the diagonals at the beam, and in particular the relevant design rules should be better calibrated. In general, results briefly presented in the current paper, in line with the literature references, delineate some important issues and suggestions for improvements, related to the design procedure and structural models. However, they require more wide elaborations through further extensive campaign of both experimental and numerical investigations aiming at both optimizing the calculation models and providing simplification to the design methods.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
The authors gratefully acknowledge the Department of Civil Protection for the research funding within the RELUIS-DPC project and Eng. Luca Canicattì for the contribution to the development of numerical analysis carried out during his bachelor’s thesis.