REVIEW ARTICLE
Optimal Sections of Tunnels’ Cross Sections with Different Overburdens
Jia Chen1, 2, Xuansheng Cheng1, 2, *, Shangrong Qi1, 2, Huan Feng1, 2, Liang Ma1, 2, Lijun Gong1, 2
Article Information
Identifiers and Pagination:
Year: 2017Volume: 11
First Page: 714
Last Page: 725
Publisher ID: TOCIEJ-11-714
DOI: 10.2174/1874149501711010714
Article History:
Received Date: 02/06/2017Revision Received Date: 22/06/2017
Acceptance Date: 23/06/2017
Electronic publication date: 21/09/2017
Collection year: 2017

open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: https://creativecommons.org/licenses/by/4.0/legalcode. This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Introduction:
In order to obtain the optimal section for super-large cross-section loess tunnels with different overburdens, the ANSYS software is applied in this paper.
Methods:
Based on the calculation nonconvergence criteria and Mohr-Coulomb criteria, the static stability of loess tunnel section is analyzed by the finite element static strength reduction method. According to the safety factors of rock mass surrounding tunnel in the case of critical failure, the safety factors of super-large cross-section loess tunnel is discussed with different section forms (rectangular cross-section, circular cross-section, horseshoe cross-section and curve wall cross-section) and different overburdens under gravity.
Results and Conclusion:
The results show that the safety factors of circular section and curve wall cross-section are bigger than the safety factors of the horseshoe cross-section and rectangular cross-section. The curve wall cross-section is considered to be the optimal section because of the fact that the force around the vault and the arch bottom is uniform and symmetrical, and the maximum vertical displacement of the lining is small. The horseshoe cross-section should be avoided in the loess tunnel, because the safety factor of horseshoe cross-section is so small, and stress concentration phenomenon is obvious in the case of deep buried tunnel.
1. INTRODUCTION
According to the existing literature, many experts and scholars have put forward many kinds of optimization design methods for the forms of tunnel section, and verified a variety of optimization design methods for the theoretical and practical aspects. Bahmanikashkooli et al. [1] calculated the critical depth of horseshoe cross-section tunnel by using particle swarm optimization. Xu Zemin et al. [2] further divided the tunnel into shallow buried tunnel, deep buried tunnel and super deep buried tunnel according to the bearing capacity of soil mass surrounding tunnel, the deformation and failure position and the deformation mode, and considered the ratio of the vertical principal stress and the minimum horizontal principal stress. Wang et al. [3] preliminarily determined the boundary value for the shallow and deep overburden of the large section loess tunnel, and obtained that the shallow buried was less than 11m, and that the boundary value of shallow and deep buried was 40m - 60m, and that the deep overburden was more than 60m. Mobaraki and Vaghefi [4] studied the dynamic response of the tunnel when the overburden of the tunnel was 3m, 5m, 7m, 10.5m and 14m, and the tunnel with different cross-section forms was analyzed by using LS-DYNA. Lu et al. [5] studied the optimal shape of the support section for deep buried tunnel, and obtained the optimal shape of the support section suggesting that the minimum value of the objective function based on the mixed compensation function method could satisfy a given constraint condition by using the conformal mapping method of plane elastic complex variable function to optimize the support section. Lv [6] obtained optimal cross-section by comparing the damage degree of soil mass surrounding tunnel with the elastic assumption, and sought optimal support cross-section shape with the assumption of the lining and rock mass contact smoothly,in other words, the stress vector and normal displacement on the contact surface satisfy the continuous condition, but the sliding between surrounding rock and lining may occur [7]. Theoretical study about stability of tunnel cross-section is carried out by Peila [8], and the corresponding force, plastic zone and displacement were respectively analyzed. Cheng et al. [9-11] proposed two new methods of seismic safety factor and fracture surface to evaluate the seismic stability of tunnel. Zheng et al. [12, 13] obtained the critical tensile failure state of tunnel by reduction parameters of soils shear strength. Cheng et al. [14] analyzed static and dynamic stability of long-span egg shaped loess tunnel without lining by strength reduction method, and obtained the influence on loess tunnel span, the thickness of covering soil and seismic intensity on safety factor and stability. Li et al. [15] investigated distribution regular of displacement and stress concentration for different cross-section forms excavated by using FLAC3D. Dong et al. [16] analyzed and calculated different cross-sections of tunnel excavated by using ANSYS. All things considered, they believe egg shaped section is the most reasonable form.
In order to get a safe, economical and reasonable section form, based on the above research, this paper will analyze the stability of different section forms and different overburdens super-large cross-section loess tunnel by using the static strength reduction method and finite element analysis software ANSYS. This provides a theoretical reference for the practical engineering application of the optimal design for the loess tunnel section.
2. CALCULATION METHOD
2.1. Shear Strength Reduction Method
Zienkiewicz et al. [17] proposed the concept of shear strength reduction coefficient for the first time in the finite element analysis of elasto-plastic soil mass. The finite element strength reduction method constantly reduced the shear strength index of the loess during the finite element model analysis until it reaches the critical failure state, and so corresponding safety factor is obtained. The traditional stability limit equilibrium method is based on the Coulomb criterion, and the safety factor is calculated by the force balance. The safety coefficient is defined as the ratio of the shear strength of slip surface τc and actual shearτ. It can be expressed as
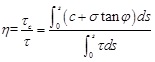 |
(1) |
where η is the safety coefficient, c and φ is respectively cohesion force and internal friction angle. Eq. (1) with both sides divided by the safety coefficient η, that is
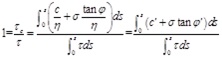 |
(2) |
where,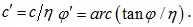
From Eq. (2), the concept of finite element static strength reduction method can be developed. The method can reflect the distribution situation of plastic zone vividly.
2.2. Failure Criterion
The ideal elastic-plastic model is used in the constitutive model of rock and soil mass in the finite element strength reduction method. It is important to select a reasonable yield criterion. At present, Coulomb criterion is widely adopted to reduce the shear strength parameters (Cohesion force c and internal friction angle φ) of rock/soil mass surrounding tunnel until the calculation does not converge by using the static analysis model. So, the safety factor of the tunnel without lining under earthquake is obtained [18-21]. That is:
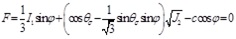 |
(3) |
where I1,J2, and θσ are the first invariant of the stress tensor, the second invariant of the stress partial tensor and the Lode angle, respectively.
Due to the yield surface of Mohr Coulomb, yield criterion is an irregular hexagonal in the π plane, the spires, edges and corners bring inconvenience to numerical calculation. So the simplified method is adopted by finite element method by using generalized Mises yield criterion. This is D-P yield criterion, and the yield surface is a circle. It can be expressed as
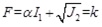 |
(4) |
where α and k areconstant which is related to the rock and soil material cohesion force c and internal friction angle φ. It can be expressed as
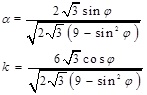 |
(5) |
3. MATERIAL PARAMETERS AND CALCULATION MODEL
3.1. Material Parameters
It was assumed that the soil mass surrounding tunnel of the whole super-large section loess tunnel structure is isotropic and ideal elastic-plastic, and the whole stress and deformation of the tunnel structure is plane strain problem and only affected by gravity. The soil mass yield criterion is based on the Mohr-Coulomb criterion. The lining concrete surrounding the tunnel is considered an elastic material. The index of physical and mechanical property for the super-large cross-section loess tunnel is shown in Table 1.
| Material | Elastic modulus E (GPa) |
Poisson’s ratio μ |
Unit weight γ (kN/m3) |
Cohesion c (MPa) |
Internal friction angle φ (°) |
|---|---|---|---|---|---|
| Soil mass | 2.0 | 0.4 | 18 | 0.14 | 25 |
| Initial lining | 31.5 | 0.2 | 25 | -- | -- |
| Secondary lining | 31.5 | 0.2 | 25 | -- | -- |
Optimal cross-section form is obtained by analyzing different overburdens because the pressure of the soil mass is affected by tunnel overburden. As an example, the depth of super shallow buried tunnel is 10m, shallow buried is 30m, deep buried is 80m. Optimal cross-section form of super-large cross-section with different tunnel overburdens is obtained by comparing the safety factor, the critical strain nephogram, the first principal stress nephogram and maximum vertical displacement nephogram of lining for super-large cross-section loess tunnel with super shallow buried, shallow buried and deep buried by using ANSYS.
3.2. Calculation Model
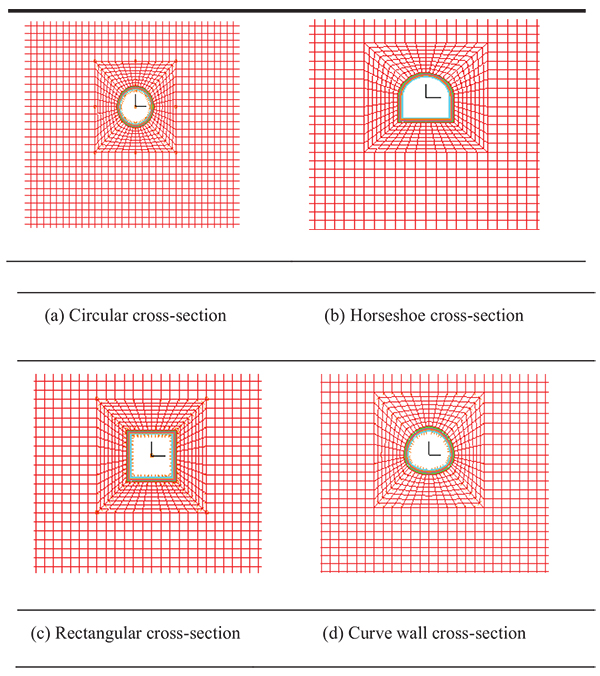
The stability analysis of the super-large cross-section loess tunnel is studied with different tunnel overburdens. The cross-section form for the super-large cross-section loess tunnel is divided into the rectangular cross-section, the circular cross-section, the horseshoe cross-section and the curve wall cross-section. The model size of each cross-section of the tunnel is 15m×15m (width×height). The calculation range is 5 times of the tunnel diameter on both sides (left side and right side) downward side on super-large cross-section loess tunnel. The tunnel overburden is 30m. The boundary conditions are: the left and right boundaries are constrained by the horizontal direction, and the bottom boundary is constrained by the vertical direction, and the top is free surface, which is free from any restriction. The calculation model of different section forms of super large section loess tunnel is shown in Table 2.
4. SECTION OPTIMIZE ANALYSIS
4.1. Static Stability Analysis in Case of Super Shallow Buried Tunnel
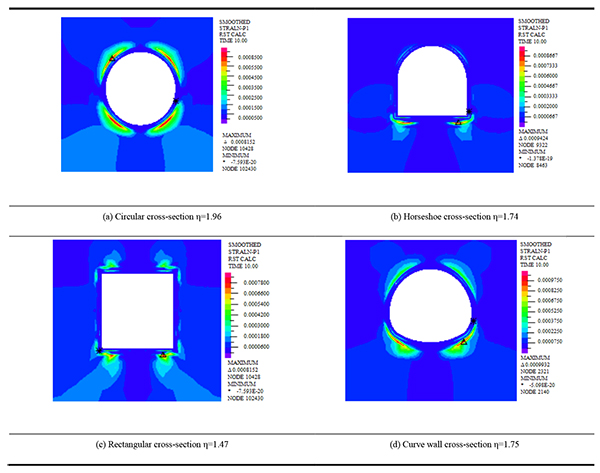
The safety factor for loess tunnel under the action of gravity can be obtained by using static finite element strength reduction method. The soil mass thickness with 800mm outside initial lining is taken as the shear strength reduction zone and the same material parameters is used by the reduction zone and soil mass. The stability of different cross-section forms with the same conditions is analyzed by comparing the safety factor, and the first principal stress and the maximum vertical displacement of the tunnel lining in the case of super shallow buried tunnel. According to the boundary value of deep and shallow buried large cross-section loess tunnel, the overburden thickness of super shallow buried tunnel is 10m. The safety factor and critical strain nephogram in the case of super shallow buried loess tunnel with different cross-section is shown in Table 3.
 |
From Table 3, the safety factor of super-large cross-section loess tunnel with different cross-sections forms can be obtained by strength reduction method. The safety factor of circular super-large cross-section is 1.96. The safety factor of horseshoe super-large cross-section is 1.74. The safety factor of rectangular super-large cross-section is 1.47. The safety factor of curve wall super-large cross-section is 1.75. This shows that the safety factors are ordered from large to small, namely, circular, curved wall, horseshoe and rectangle cross-section. The safety factors of the horseshoe and curve wall cross-section is almost the same, but they differ greatly from the safety factor of rectangular cross-section.
 |
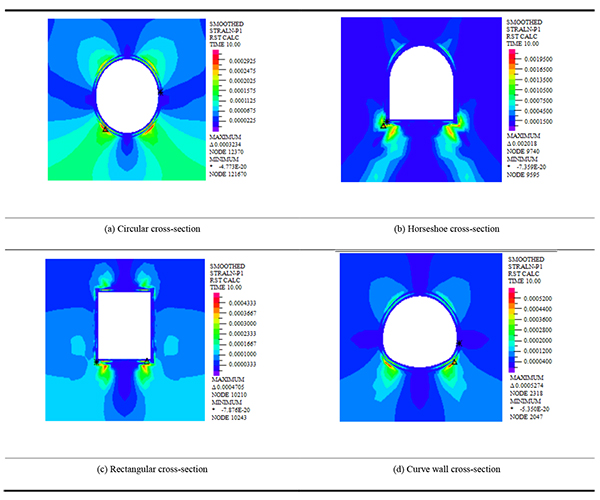 |
From critical strain nephogram, in the case of super shallow buried tunnel, strain in the arch feet and the vault are more concentrated, and the maximum critical strain occurs at the bottom of the arch, and the range of cross-section strain increases with the increase in the safety factor. The critical first principal stress nephogram in the case of super shallow buried loess tunnel with different cross-sections is shown in Table 4.
From Table 4, tensile stress appears in the vault and arch bottom, the maximum tensile stress occurs at the arch feet, and the range of stress nephogram increases with the increase in the safety factor. This shows that the force cross-section bore increases with the increase in the safety factor. The stress distribution of circular cross-section is more uniform, and the stress of rectangle and horseshoe is more concentrated. The maximum vertical displacement nephogram of lining in the case of super shallow buried loess tunnel with different cross-sections is shown in Table 4.
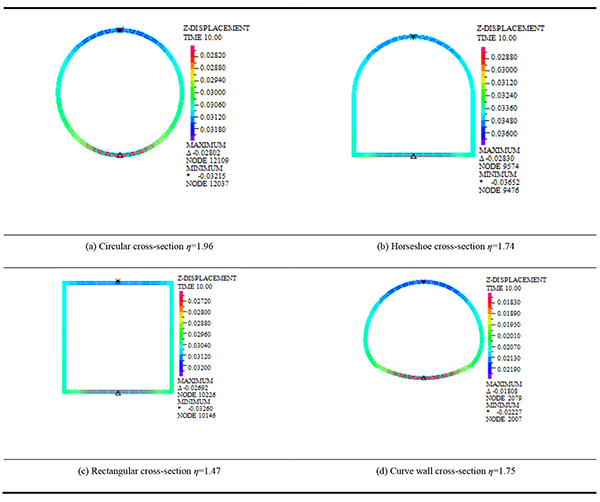 |
Table 5 shows that the maximum vertical displacement occurs in the vault. The maximum vertical displacement of lining for circular cross-section is 32.15mm. The maximum vertical displacement of lining for horseshoe cross-section is 36.52mm. The maximum vertical displacement of lining for rectangular cross-section is 32.6mm. The maximum vertical displacement of lining for curve wall cross-section is 22.27mm. The maximum vertical displacement of lining for super-large cross-sections loess tunnel with different cross-sections ranges from small to large, namely, curve wall, circular, rectangular, horseshoe cross-section. This shows that the optimal cross-section of the super-large cross-section loess tunnel is the circular and the curve wall cross-section in the case of super shallow buried tunnel.
4.2. Static Stability Analysis in Case of Shallow Buried Tunnel
According to the boundary value of deep and shallow buried large cross-section loess tunnel, the overburden thickness of shallow buried tunnel is 30m. The process of analysis is similar to the static stability analysis for super shallow buried tunnel. The safety factor and critical strain nephogram in the case of shallow buried tunnel are shown in Table 6.
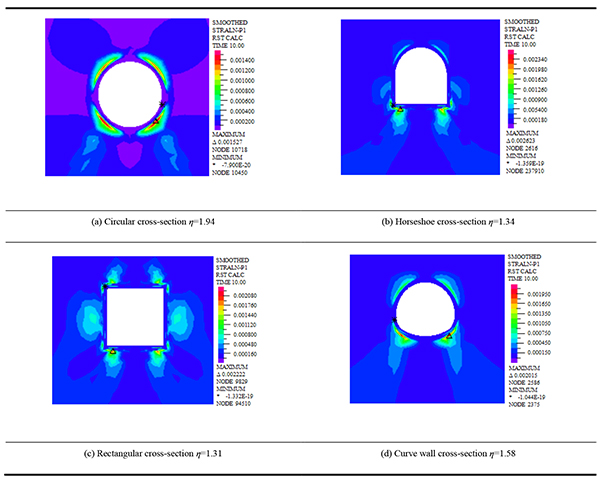 |
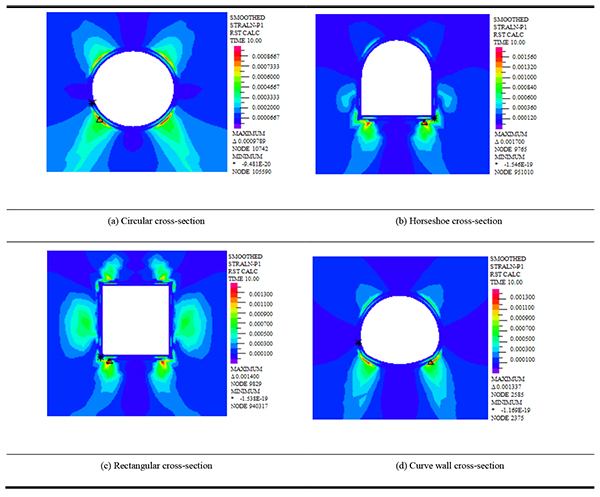 |
Table 6 shows that the safety factor of super-large cross-section loess tunnel with different cross-section forms can be obtained by strength reduction method. The safety factor of circular super-large cross-section is 1.94. The safety factor of horseshoe super-large cross-section is 1.34. The safety factor of rectangular super-large cross-section is 1.31. The safety factor of curve wall super-large cross-section is 1.58. This shows that the safety factors are ordered from large to small, namely, circular, curved wall, horseshoe and rectangle cross-section. From critical strain nephogram, the strain in the arch feet and the vault is more concentrated, and the range of cross-section strain increases with the increase of the safety factor. The critical first principal stress nephogram in the case of shallow buried loess tunnel with different cross-sections is shown in Table 7.
Table 7 shows that the maximum stress appears in the vault and arch feet, and the range of stress nephogram increases with the increase of the safety factor. This shows that the bearing capacity of cross-section increases with the increase in the safety factor. The stress distribution of circular and curve wall cross-section is more uniform, and the stresses of rectangle and horseshoe cross-section are more concentrated. Compared with the critical first principal stress of the super shallow buried loess tunnel with the overburden of 10m, the critical first principal stress of the shallow buried loess tunnel is increased. The maximum vertical displacement nephogram of lining in the case of shallow buried loess tunnel with different cross-sections is shown in Table 8.
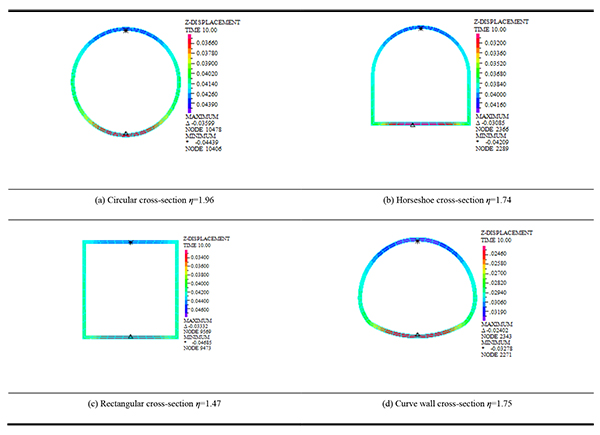 |
Table 8 shows that the maximum vertical displacement occurs in the vault. The maximum vertical displacement of lining for circular cross-section is 44.39mm. The maximum vertical displacement of lining for horseshoe cross-section is 42.09mm. The maximum vertical displacement of lining for rectangular cross-section is 46.85mm. The maximum vertical displacement of lining for curve wall cross-section is 32.78mm. The maximum vertical displacement of lining for super-large cross-sections loess tunnel with different cross-sections starting from large to small, namely, curve wall, horseshoe, circular, and rectangular cross-section. Compared with the super shallow buried tunnel, the maximum vertical displacement of the lining for the shallow buried tunnel is increased. This shows that the optimal cross-section of the super-large cross-section loess tunnel is the circular and the curve wall cross-section in the case of shallow buried tunnel. Meanwhile, it shows that the stress of the super-large cross-section loess tunnel in the case of shallow buried is greater than the stress in the case of super shallow buried.
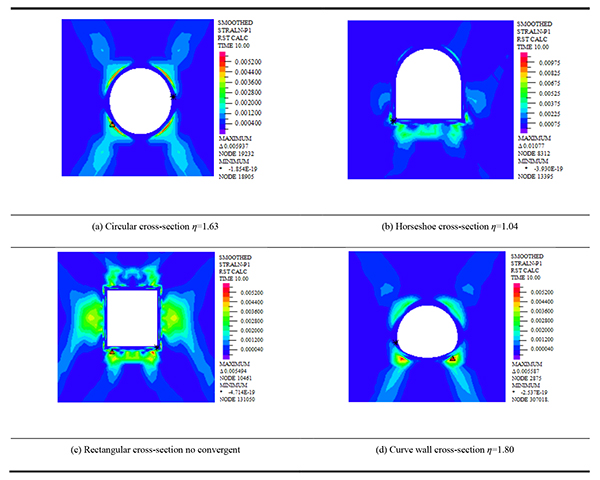 |
4.3. Static Stability Analysis in Case of Deep Buried Tunnel
According to the boundary value of deep and shallow buried large cross-section loess tunnel, the overburden thickness of deep-buried tunnel is 80m. The process of analysis is similar to the static stability analysis for super shallow buried tunnel. The safety factor and critical strain nephogram in the case of deep-buried tunnel are shown in Table 9.
From Table 9, the safety factor of super-large cross-section loess tunnel can be obtained by strength reduction method in the case of deep buried tunnel with different cross-sections forms. The safety factor of circular super-large cross-section is 1.63. The safety factor of horseshoe super-large cross-section is 1.04. The rectangular super-large cross-section does not converge. The safety factor of curve wall super-large cross-section is 1.80. This shows that the safety factors are ordered from large to small, namely curved wall, circular, horseshoe cross-section. From critical strain nephogram, strain occurs in the arch feet and the vault, and the range of cross-section strain increases with the increase of the safety factor. This shows that the safety factor of the super-large cross-section loess tunnel with different cross-sections in the case of super shallow buried, shallow-buried and deep-buried are ordered from large to small, namely circular, curve wall, horseshoe, and rectangular cross-section. The critical first principal stress nephogram in the case of deep-buried loess tunnel with different cross-sections is shown in Table 10.
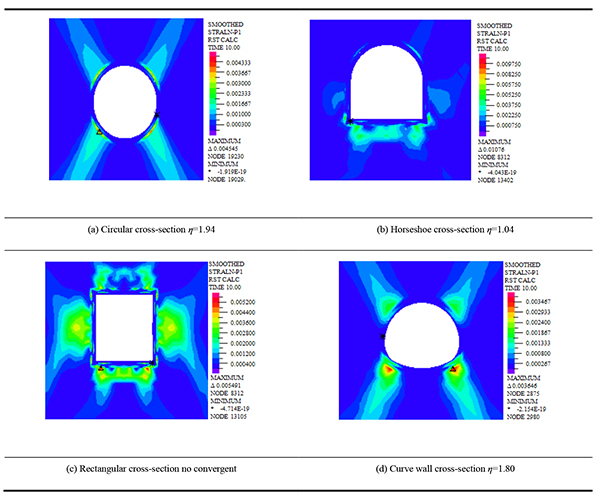 |
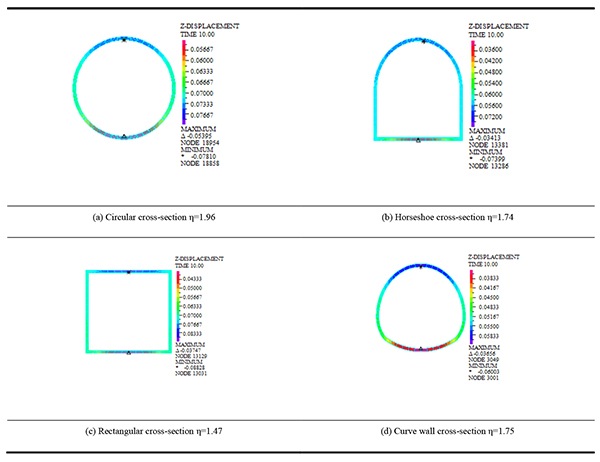 |
Table 11. Shows that the maximum vertical displacement occurs in vault in the case of deep-buried tunnel. The maximum vertical displacement of lining for circular cross-section is 78.10mm. The maximum vertical displacement of lining for horseshoe cross-section is 73.99mm. The maximum vertical displacement of lining for rectangular cross-section is 88.28mm. The maximum vertical displacement of lining for curve wall cross-section is 60.03mm. The maximum vertical displacement of lining for super-large cross-section loess tunnel with different cross-sections occurs from small to large, namely, curve wall, horseshoe, circular, rectangular cross-section. The maximum first principal stress of tunnel appears at the bottom of arch, and the stress distribution of the circular and the curve wall cross-section is more uniform and symmetrical, but the stress distribution of the rectangular and the horseshoe cross-section is not uniform. Compared with the super shallow buried and shallow-buried loess tunnel, the maximum vertical displacement of the lining for the deep buried tunnel occurs in vault and increases with the increase of overburden. This shows that the pressure and the maximum vertical displacement of the lining for loess tunnel increase with the increase of the depth of loess tunnel.
Table 10 shows that the maximum first principal stress of the super-large cross-section loess tunnel occurs at the arch feet. The stress distribution of circular and curve wall cross-section is more uniform in vault and arch feet, and the stress of horseshoe cross-section is more concentrated in arch bottom. The stress distribution of the rectangular cross-section is around the tunnel, and the maximum stress occurs at the arch feet. Compared with the critical first principal stress of the super shallow buried and shallow buried loess tunnel, the critical first principal stress of the deep buried loess tunnel is gradually increased. This shows that the force cross-section bore increases with the increase of the thickness of cover layer. The maximum vertical displacement nephogram of lining in the case of deep-buried loess tunnel with different cross-sections is shown in Table 11.
CONCLUSION
- In the case of super shallow buried tunnel, the range of cross-section strain and stress for super-large cross-section loess tunnel increases with the increase of the safety factor and the maximum critical strain occured at the bottom of arch. The cross-section for maximum vertical displacement of the lining is the horseshoe cross-section.
- In the case of shallow buried tunnel, the maximum stress of the super-large cross-section loess tunnel occurs at the arch feet and the vault. The safety factor of rectangular cross-section is the smallest in the four different cross-sections, and the rectangular cross-section bears the greatest stress. The cross-section for the maximum vertical displacement of the lining is rectangular cross-section.
- The horseshoe cross-section should be avoided in the loess tunnel, because the safety factor of horseshoe cross-section is so small, and stress concentration phenomenon is obvious in the case of deep-buried tunnel.
- The curve wall cross-section is considered to be the optimal cross-section due to the fact that the force around the vault and the arch bottom is uniform and symmetrical, and the maximum vertical displacement of the lining is small. In addition, the safety factor of curve wall cross-section is large.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
This paper is a part of the national natural science foundation of China (Grant number: 51478212), and a part of the education ministry doctoral tutor foundation of China (Grant number: 20136201110003), and a part of science & technology development project of China railway 21 group Co., LTD (Grant number: 14B-3).







