Design Reliability Analysis of Cold-Formed Thin-Walled Steel Members with Lipped Channel Sections Considering Distortional Buckling

All published articles of this journal are available on ScienceDirect.

RESEARCH ARTICLE

Design Reliability Analysis of Cold-Formed Thin-Walled Steel Members with Lipped Channel Sections Considering Distortional Buckling

Yao Xingyou1 , 2 , * Open Modal
Authors Info & Affiliations
The Open Civil Engineering Journal • 21 Nov 2017 • RESEARCH ARTICLE • DOI: 10.2174/1874149501711010906

Abstract

Introduction:

Based on the experimental results of cold-formed thin-walled steel lipped channel sections, the uncertainty of calculating mode of load-carrying capacity using effective width method considering distortional buckling for different material types cold-formed steel compressed members was researched, and the uncertainties of material strength and geometric characteristics of the typical sections were statistically analyzed.

Methods:

According to the recommended resistance of partial coefficient in the draft of Technical code of cold-formed steel structures (GB50018-), the reliability indexes of cold-formed thin-walled steel lipped channel sections under compression were investigated using the improved first-order second-moment method considering different possible external loading combinations.

Results:

The analyzed results show that, using the recommended resistance partial coefficient in the code draft, the reliability indexes of the compressed members with width-thickness ratio within the limitation of code draft can well met the target reliability index. The suitability of the corresponding calculating modes of load-carrying capacity considering distortional buckling was established.

Keywords: Cold-formed thin-walled steel, Lipped channel sections, Distortional buckling, Effective width method, Reliability, Width-thickness.

1. INTRODUCTION

Cold-formed lipped channel sections have been widely used in residential and commercial construction recently. Distortional buckling occurs for cold-formed thin-walled lipped channel sections under compressed load because of large width-to-thickness ratio of the flanges and weak torsional restraint of lip to flange. The direct strength method has been put forward to estimate the distortional buckling strength of lipped channel sections based on the test and theoretical analysis [1-5]. The distortional buckling mechanical behavior and design method were studied for lipped channel sections fabricated with LG550, S350, S280 steel plates [6-10]. Then recommend design method for distortional buckling strength was given [11]. The reliability analysis of the recommend method show that the design method in Chinese code considering distortional buckling is suitable for lipped channel sections fabricated with LG550 [12], S350 [13], S280 [14] steel plates if the suitable resistance partial coefficient is used.

To simplify the calculated method of distortional buckling load-carrying capacities for lipped channel sections, a study [15, 16] has given the improved width method considering the distortional buckling using energy method based on the test results. The design reliability of the cold-formed thin-walled steel members with lipped channel sections considering distortional buckling for different material type cold-formed steel compressed members was researched using the improved first-order second-moment method based on the experimental results in this paper.

2. LITERATURE REVIEW ON DISTORTIONAL BUCKLING EXPERIMENTS

The detailed distortional buckling experiments for lipped channel sections fabricated with LG550, S350, S280 steel plates can be found in reference [6-10]. These experiments include axially compressed members and eccentrically compressed members for lipped channel sections fabricated with LG550, S350, S280 steel plates. The eccentrical experiments include bending about strong axial, bending about weak axial (eccentric to web), and bending about weak axial (eccentric to web).The overall view of compressed columns tests arrangements is shown in Fig. (1). The columns were fixed supported for axially compressed stud columns. The other column specimens were used to simulate the hinged-hinged support using two knife hinges at every end.

Fig. (1). Overall view of compressed columns tests setup.

The typical buckling mode for LG550 axially compressed members is shown in Fig. (2). Distortional buckling and local buckling occurred for stud columns, medium columns, and columns bending about strong axial. Distortional buckling and overall flexural buckling occurred for long members. The buckling mode for S350 and S280 axially compressed members was observed to be same to the LG550 members.

Fig. (2). Typical buckling mode for axially compressed columns.

The typical buckling mode for LG550 eccentrically compressed members is shown in Fig. (3). Distortional buckling took place for the specimens bending about weak axial and load was eccentric to lip (Fig. 3a) and bending about strong axial (Fig. 3b). With the increase of the slenderness ratio, the interaction among distortional buckling and overall buckling occurred for the specimens bending about weak axial and load was eccentric to the lip (Fig. 3c) and bending about strong axial (Fig. 3d).The interaction among local buckling and overall buckling occurred for the specimens bending about weak axial and load was eccentric to web (Fig. 3e). The buckling mode for S350 and S280 eccentrically compressed members were observed to be same to the LG550 members.

Fig. (3). Typical buckling mode for eccentrically compressed columns.

The tested ultimate tested compressive load strength and buckling mode for all specimens can be found in reference [6-10].

3. MATERIALS AND METHOD

3.1. Effective Width Method Considering Distortional Buckling

Distortional buckling occurs for cold-formed thin-walled lipped channel sections under compressed load because of large width-to-thickness ratio of the flanges and weak torsional restraint of lip to flange. A study [17] showed the improved calculation method for cold-formed thin-walled lipped channel sections considering the distortional buckling using the effect width method based on Chinese code GB50018-2002 [18], and the buckling stability coefficient of the partially stiffened plates is calculated as follows:

If maximum stress acts on the stiffened edge:

(1)
(2)

and the calculated value should be less than the calculated value using formula (1).

If maximum stress acts on the partially stiffened edge:

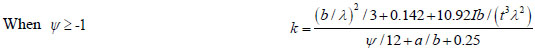(3)

and the calculated value should be less than the calculated value using formula (1).

Where ψ is the factor of non-uniform stress distribution for the partially stiffened element, b is the width of the partially stiffened element, a is the width of lip,t is the thickness of member,I is the lip moment of inertia about the central axis of the lip and the partially stiffened plate, which can be calculated as:

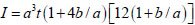(4)

λ is the minimum of distortional buckling half-wavelength and length of member. Distortional buckling half-wave length can be obtained as follows:

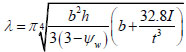(5)

Where h is the height of adjacent stiffened elements, ψw is the uneven coefficient of the compression stress distribution of the adjacent stiffened element.

4. STATISTICAL ANALYSIS OF RESISTANCE UNCERTAINTY

4.1. Variation in the Material Strength

There are two factors which affect the material strength, the material strength fy tested using the standard coupons and the disparity coefficient, K0 , considering the difference of the strength value between a standard specimen and the practical engineering material. K0 is equal to 0.94 [19] for cold-formed thin-walled steel structures. So the material strength is equal to fyK0 . Based on the analyzed results of the current steel productions for LQ550 [12] less than 1.6mm and S350 [13] and S280 [14] less than 2mm, the statistical analysis results of the different grade steel plates are listed in Table 1. The material strengths are normal distributions when the significance level is less than 5%.

Table 1.
Statistical analysis of the yield strength of steel sheets.
Grade Thickness Number
n 		μfy/MPa σfy/MPa μKfy μKM VKM
LG550 A t < 0.6mm 528 724.8786 20.2302 1.3180 1.2389 0.0279
B 0.6mm≤ t ≤ 0.9mm 3396 664.3919 20.9933 1.2080 1.1355 0.0316
C 0.9mm< t ≤ 1.2mm 1552 595.5714 22.3948 1.0829 1.0179 0.0376
D t > 1.2mm 2579 538.3253 16.2784 0.9788 0.9200 0.0302
S350 0.6mm≤ t ≤ 2.0mm 73 407.1762 34.6437 1.1634 1.0936 0.0851
S280 0.6mm≤ t ≤ 2.0mm 41 322.7982 23.0693 1.1529 1.0837 0.0715

4.2. Variation of the Geometric Characteristics

Variation in the geometric characteristics of the structural members includes the dimensional error during fabrication and erection. The fabricated geometric section characteristics of a section should mainly be considered for cold-formed thin-walled steel members. The geometric section characteristics of a section are determined by the geometric shapes, dimension of the cross section, and the situation of external load. The geometric section characteristics are assumed as:

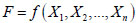(6)

Where X1,X2,Xn are random variables affecting the geometric section characteristics.

The standard deviation σF and variation coefficient VF of F can be obtained using the error transfer theory [20].

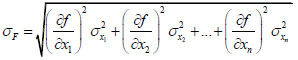(7)
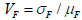(8)

It is assumed that the uncertainty of geometric section characteristics KF is equal to the ratio of the measured results to the normal values. The mean value μKF and variation coefficient VKF are calculated using formula (6)-(8).

The statistical results of the geometric characteristics are shown in Table 2 based on the analysis of cold-formed steel lipped channel sections. The uncertainty of geometric characteristics is normal distribution when the significance level is less than 5%.

Table 2.
Uncertainty of geometric characteristics of cold-formed thin-walled steel members.
Grade Member type Uncertainty of geometric characteristics KF
Mean Variation coefficient
LG550 A axially-compressed members 0.9992 0.0169
B 0.9948 0.0154
C 0.9968 0.0135
D 0.9977 0.0097
A eccentrically-compressed members 1.0303 0.0333
B 1.0320 0.0205
C 1.0405 0.0137
D 1.0493 0.0082
S350 axially-compressed members 1.0254 0.0108
eccentrically-compressed members 1.0359 0.0120
S280 axially-compressed members 1.0391 0.0466
eccentrically-compressed members 1.0466 0.0331

4.3. Variation of Uncertainty of the Calculation Model

The uncertainty of the calculation method is because of the error between the theoretical values and the calculated results, which can be determined according to the ratio of the test results to the calculated results using recommend method. The load-carrying capacities of the cold-formed steel lipped channel members shown in references [6-10, 21], were calculated using the recommend method in this paper as shown in reference [18]. The uncertainty of the calculation method is defined as KP = Pt/P0 , where Pt and P0 are the test result and the calculated values using the recommend method, respectively. The statistical results of the calculation method are shown in Table 3. The uncertainty of the calculation method was observed in normal distributions when the significance level was less than 5% using Kolmogorov-Smirnov test method.

Table 3.
Uncertainty of calculation method of cold-formed thin-walled steel members.
Grade Member type Number Uncertainty of calculation method KP
Mean Variation coefficient
LG550 B axially-compressed members 15 1.1073 0.1675
C 48 1.1440 0.1662
B eccentrically-compressed members 13 0.9615 0.2928
C 35 1.0977 0.1973
S350 axially-compressed members 26 1.0769 0.1084
eccentrically-compressed members 33 1.1307 0.1533
S280 axially-compressed members 19 1.0555 0.0565
eccentrically-compressed members 56 1.2363 0.1252

4.4. Variation of the Resistance of Structural Members

The resistance of cold-formed thin-walled steel members [20] is given as:

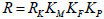(9)

Where RK, KM, KF, and KP are the characteristics value of the resistance of cold-formed steel members, uncertainty of the material strength of cold-formed steel members, uncertainty of the geometric characteristics of cold-formed steel members, and uncertainty of the calculation method of cold-formed steel members, respectively.

KM, KF, and KP are assumed to be independent of each other. The mean and the standard deviation of the variation coefficient of the resistant of cold-formed thin-walled steel members can be given as formula (10) and (11) using the linearization rule.

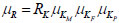(10)
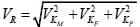(11)

If KR is defined as the ratio value of mean resistant to the characteristics value of the resistant of cold-formed thin-walled steel members, KR= R / RK, the mean value of KR can be obtained as:

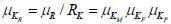(12)

The resistant R is the product of several variables with normal probability distribution, as shown in formula (10). Because uncertainty of the material strength, of the geometric characteristics and of the calculation method of cold-formed steel members had normal probability distribution, the resistant will have a logarithm normal distribution. The statistical parameters of the resistance model uncertainty of the cold-formed thin-walled steel lipped channel compression members fabricated with LQ550, S350, and S280 cold-formed thin-walled steel plates are listed in Table 4.

Table 4.
Statistical analysis of resistance uncertainty of cold-formed thin-walled steel members.
Grade Member type KM KF KP R
Mean Variation coefficient Mean Variation coefficient Mean Variation coefficient Mean Variation coefficient
LG550 A axially-compressed members 1.2389 0.0279 0.9992 0.0169 1.1073 0.1675 1.3707 0.1706
B 1.1355 0.0316 0.9948 0.0154 1.1073 0.1675 1.2508 0.1711
C 1.0179 0.0376 0.9968 0.0135 1.144 0.1662 1.1608 0.1709
D 0.9200 0.0302 0.9977 0.0097 1.144 0.1662 1.0501 0.1692
A eccentrically-compressed members 1.2389 0.0279 1.0303 0.0333 1.0469 0.1979 1.3363 0.2026
B 1.1355 0.0316 1.0320 0.0205 1.0469 0.1979 1.2268 0.2015
C 1.0179 0.0376 1.0405 0.0137 1.0977 0.1973 1.1626 0.2013
D 0.9200 0.0302 1.0493 0.0082 1.0977 0.1973 1.0597 0.1998
S350 axially-compressed members 1.0936 0.0851 1.0254 0.0108 1.0769 0.1084 1.2076 0.1382
eccentrically-compressed members 1.0936 0.0851 1.0359 0.0120 1.1318 0.1038 1.2821 0.1348
S280 axially-compressed members 1.0837 0.0715 1.0391 0.0466 1.0555 0.0565 1.1886 0.1024
eccentrically-compressed members 1.0837 0.0715 1.0466 0.0331 1.2363 0.1252 1.4022 0.1479

5. STATISTICAL PARAMETERS OF THE UNCERTAINTIES OF EXTERNAL LOADS AND LOAD COMBINATION

5.1. Statistical Parameters of the Uncertainties of Different External Loads

Statistical parameters of the uncertainties of different external loads in China can be obtained according to the existing research results [22], as shown in Table 5.

Table 5.
Statistical parameters of different external loads.
Load type Statistical parameters Distribution
Mean Variation coefficient
Dead load G 1.060 0.070 Normal
Live load(office)L 0.524 0.288 Extreme I
Live load(residence)L 0.644 0.230 Extreme I
Wind load W 0.908 0.193 Extreme I

5.2. Load Combination

Two kinds of load combination cases are considered for cold-formed thin-walled steel members based on the Load code for the design of building structures GB50009-2001.

1)The design formula for the combination of dead load, live load, and wind load is given as:

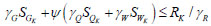(13)

2)The design formula for the combination of dead load, live load is given as:

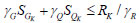(14)

Where γG, γQ, and γW are the partial coefficient of the characteristic value of dead load, live load, and wind load, respectively. ψ is the load combination coefficient. SGk, SLk, and SWk are the characteristic value of dead load, live load, and wind load, respectively. RK is the characteristic value of the resistance; γR is the resistance partial coefficient.

The 24 external load combination cases considered are listed in Table 6. Where ρ1 is the ratio values of the sum of the characteristic value of live load and the characteristic value of wind load to the characteristic value of dead load, while ρ2 is the ratio values of the characteristic value of wind load to the characteristic value of dead load.

Table 6.
External loads combination case.
Load combination case Load ratio
ρ1 = (SLk + SWk)/SGk ρ2 = SWk / SLk
G+ L 0.5,1.0,2.0,3.0
G+ L+W 0.5,1.0,2.0,3.0 0.5,1.0,2.0,3.0,4.0

6. DESIGN RELIABILITY ANALYSIS

6.1. Reliability Index of Structural Members

The determination of a suitable target reliability index for cold-formed steel structures can be obtained by the draft of Technical code of cold-formed steel structure [23] based on Unified standard of reliability design for building structures as shown in Table 7 [24]. Considering the ductility characteristics of cold-formed steel, the target reliability index of Grade A, Grade B, Grade C, and Grade D for LG550 high-strength steel are 3.5, 3.4, 3.3, and 3.2,respectively. The target reliability index of S350 and S280 steel are 3.2.

Table 7.
Reliability index for structural members based on ultimate limited state design.
Facture type Safety grades
I I I I I I
Ductile 3.7 3.2 2.7
Brittle 4.2 3.7 3.2

6.2. Design Reliability Analysis of Members

The resistance partial coefficient is equal to 1.165 for S350, S280, and LG550 compressed members according to the Technical code of cold-formed steel structure (Draft) [23] and Technical specification for low-rise cold-formed thin-walled steel buildings [11]. The standard strength and the recommended design strength for S350, S280, and LG550 steel are shown in Table 8.

Table 8.
Standard strength and recommended design strength.
Steel grade Thickness Yeild strength/MPa Design strength/MPa
LG550 A t < 0.6mm 530 455
B 0.6mm≤t≤0.9mm 500 430
C 0.9mm<t≤1.2mm 460 400
D t>1.2mm 420 360
S350 0.6mm≤t≤2.0mm 350 300
S280 0.6mm≤t≤2.0mm 280 240

Based on the resistance uncertainty of cold-formed thin-walled steel members and uncertainties of external loads, the reliability index for S350, S280, and LG550 axially and eccentrically compressed members can be calculated as shown in Tables 9-20 using the improved first-order second-moment method under 24 kinds of external loads combinations.

Table 9.
Reliability index for LG550 cold-formed thin-walled steel axially-compressed members (Residence).
Grade ρ2 = SWk / SLk ρ1 = (SLk + SWk)/SGk Mean
0.5 1.0 2.0 3.0
A 0 4.374 4.470 4.398 4.347 4.397
0.5 4.136 4.378 4.433 4.417 4.341
1.0 4.062 4.291 4.372 4.369 4.274
2.0 3.959 4.080 4.046 4.000 4.021
3.0 3.897 3.955 3.872 3.810 3.884
4.0 3.858 3.878 3.770 3.702 3.802
B 0 4.182 4.311 4.261 4.219 4.243
0.5 3.932 4.188 4.267 4.260 4.162
1.0 3.858 4.096 4.196 4.203 4.088
2.0 3.756 3.895 3.884 3.847 3.846
3.0 3.697 3.776 3.715 3.663 3.713
4.0 3.660 3.703 3.617 3.557 3.634
C 0 4.174 4.303 4.255 4.213 4.236
0.5 3.924 4.180 4.259 4.253 4.154
1.0 3.849 4.088 4.189 4.195 4.080
2.0 3.748 3.887 3.876 3.840 3.838
3.0 3.689 3.768 3.708 3.656 3.705
4.0 3.651 3.695 3.610 3.550 3.626
D 0 4.236 4.351 4.293 4.248 4.282
0.5 3.989 4.241 4.310 4.300 4.210
1.0 3.914 4.151 4.243 4.245 4.138
2.0 3.811 3.944 3.923 3.883 3.890
3.0 3.751 3.821 3.752 3.696 3.755
4.0 3.712 3.746 3.652 3.588 3.675
Table 10.
Reliability index for LG550 cold-formed thin-walled steel axially-compressed members (Office).
Grade ρ2 = SWk / SLk ρ1 = (SLk + SWk)/SGk Mean
0.5 1.0 2.0 3.0
A 0 4.554 4.653 4.581 4.532 4.580
0.5 4.276 4.559 4.618 4.602 4.514
1.0 4.167 4.438 4.535 4.536 4.419
2.0 4.027 4.169 4.141 4.097 4.108
3.0 3.947 4.018 3.939 3.879 3.946
4.0 3.898 3.927 3.822 3.755 3.850
B 0 4.366 4.501 4.451 4.410 4.432
0.5 4.073 4.374 4.459 4.453 4.339
1.0 3.963 4.245 4.364 4.374 4.236
2.0 3.825 3.986 3.982 3.947 3.935
3.0 3.748 3.840 3.784 3.734 3.776
4.0 3.699 3.752 3.670 3.612 3.683
C 0 4.358 4.494 4.445 4.404 4.425
0.5 4.065 4.366 4.452 4.446 4.332
1.0 3.955 4.237 4.356 4.367 4.229
2.0 3.816 3.978 3.974 3.940 3.927
3.0 3.739 3.832 3.777 3.727 3.769
4.0 3.691 3.744 3.663 3.605 3.676
D 0 4.419 4.539 4.481 4.437 4.469
0.5 4.131 4.426 4.500 4.490 4.387
1.0 4.021 4.299 4.410 4.416 4.287
2.0 3.880 4.034 4.020 3.982 3.979
3.0 3.801 3.885 3.820 3.766 3.818
4.0 3.752 3.796 3.705 3.643 3.724
Table 11.
Reliability index for LG550 cold-formed thin-walled steel eccentrically-compressed members (Residence).
Grade ρ2 = SWk / SLk ρ1 = (SLk + SWk)/SGk Mean
0.5 1.0 2.0 3.0
A 0 3.667 3.913 3.967 3.960 3.877
0.5 3.411 3.680 3.843 3.882 3.704
1.0 3.344 3.585 3.744 3.789 3.616
2.0 3.263 3.438 3.513 3.518 3.433
3.0 3.218 3.352 3.382 3.369 3.330
4.0 3.190 3.299 3.304 3.281 3.268
B 0 3.551 3.810 3.876 3.874 3.778
0.5 3.291 3.564 3.736 3.780 3.593
1.0 3.223 3.468 3.634 3.683 3.502
2.0 3.142 3.322 3.406 3.415 3.322
3.0 3.098 3.238 3.278 3.269 3.221
4.0 3.070 3.185 3.200 3.182 3.159
C 0 3.640 3.888 3.943 3.938 3.852
0.5 3.382 3.652 3.817 3.857 3.677
1.0 3.345 3.557 3.718 3.763 3.588
2.0 3.333 3.410 3.486 3.491 3.405
3.0 3.330 3.370 3.376 3.354 3.340
4.0 3.308 3.323 3.355 3.342 3.302
D 0 3.724 3.962 4.005 3.995 3.921
0.5 3.468 3.737 3.894 3.929 3.757
1.0 3.401 3.642 3.797 3.839 3.670
2.0 3.318 3.491 3.559 3.560 3.482
3.0 3.272 3.403 3.425 3.408 3.377
4.0 3.243 3.347 3.345 3.318 3.313
Table 12.
Reliability index for LG550 cold-formed thin-walled steel eccentrically-compressed members (Office).
Grade ρ2 = SWk / SLk ρ1 = (SLk + SWk)/SGk Mean
0.5 1.0 2.0 3.0
A 0 3.845 4.119 4.173 4.166 4.076
0.5 3.537 3.861 4.048 4.090 3.884
1.0 3.438 3.724 3.911 3.964 3.759
2.0 3.324 3.525 3.613 3.621 3.521
3.0 3.263 3.415 3.453 3.442 3.393
4.0 3.225 3.347 3.359 3.337 3.317
B 0 3.731 4.020 4.086 4.084 3.980
0.5 3.417 3.748 3.945 3.992 3.776
1.0 3.318 3.608 3.803 3.861 3.648
2.0 3.204 3.411 3.509 3.521 3.411
3.0 3.143 3.302 3.350 3.343 3.284
4.0 3.106 3.235 3.256 3.240 3.209
C 0 3.819 4.095 4.150 4.144 4.052
0.5 3.508 3.835 4.024 4.066 3.858
1.0 3.409 3.696 3.886 3.939 3.733
2.0 3.395 3.497 3.587 3.595 3.494
3.0 3.333 3.387 3.426 3.416 3.365
4.0 3.315 3.369 3.382 3.361 3.332
D 0 3.903 4.166 4.209 4.198 4.119
0.5 3.595 3.919 4.098 4.135 3.936
1.0 3.495 3.781 3.964 4.013 3.813
2.0 3.380 3.579 3.659 3.663 3.570
3.0 3.318 3.466 3.496 3.480 3.440
4.0 3.279 3.396 3.399 3.374 3.362
Table 13.
Reliability index for S350 cold-formed thin-walled steel axially-compressed members (Residence).
ρ2 = SWk / SLk ρ1 = (SLk + SWk)/SGk Mean
0.5 1.0 2.0 3.0
0 4.133 4.185 4.095 4.042 4.113
0.5 3.889 4.132 4.152 4.123 4.074
1.0 3.804 4.045 4.098 4.081 4.007
2.0 3.674 3.780 3.718 3.664 3.709
3.0 3.597 3.630 3.524 3.457 3.552
4.0 3.548 3.540 3.412 3.340 3.460
Table 14.
Reliability index for S350 cold-formed thin-walled steel axially-compressed members (Office).
ρ2 = SWk / SLk ρ1 = (SLk + SWk)/SGk Mean
0.5 1.0 2.0 3.0
0 4.328 4.379 4.291 4.240 4.310
0.5 4.052 4.328 4.349 4.321 4.263
1.0 3.928 4.209 4.275 4.261 4.168
2.0 3.754 3.878 3.822 3.770 3.806
3.0 3.655 3.699 3.597 3.533 3.621
4.0 3.593 3.593 3.469 3.398 3.513
Table 15.
Reliability index for S350 cold-formed thin-walled steel eccentrically-compressed members (Residence).
ρ2 = SWk / SLk ρ1 = (SLk + SWk)/SGk Mean
0.5 1.0 2.0 3.0
0 4.558 4.513 4.368 4.296 4.434
0.5 4.371 4.549 4.499 4.445 4.466
1.0 4.288 4.485 4.473 4.430 4.419
2.0 4.144 4.178 4.051 3.974 4.087
3.0 4.055 4.009 3.841 3.753 3.915
4.0 3.998 3.909 3.722 3.628 3.814
Table 16.
Reliability index for S350 cold-formed thin-walled steel eccentrically-compressed members (Office).
ρ2 = SWk / SLk ρ1 = (SLk + SWk)/SGk Mean
0.5 1.0 2.0 3.0
0 4.738 4.692 4.550 4.480 4.615
0.5 4.531 4.730 4.680 4.626 4.642
1.0 4.411 4.642 4.640 4.599 4.573
2.0 4.223 4.271 4.148 4.073 4.179
3.0
4.0		 4.112 4.073 3.910 3.823 3.980
4.042 3.959 3.775 3.683 3.865
Table 17.
Reliability index for S280 cold-formed thin-walled steel axially-compressed members (Residence).
ρ2 = SWk / SLk ρ1 = (SLk + SWk)/SGk Mean
0.5 1.0 2.0 3.0
0 4.780 4.570 4.353 4.260 4.491
0.5 4.758 4.755 4.580 4.486 4.645
1.0 4.681 4.743 4.597 4.508 4.632
2.0 4.449 4.305 4.074 3.965 4.198
3.0 4.305 4.086 3.830 3.715 3.984
4.0 4.217 3.961 3.693 3.576 3.862
Table 18.
Reliability index for S280 cold-formed thin-walled steel axially-compressed members (Office).
ρ2 = SWk / SLk ρ1 = (SLk + SWk)/SGk Mean
0.5 1.0 2.0 3.0
0 4.950 4.742 4.533 4.444 4.667
0.5 4.928 4.925 4.753 4.663 4.817
1.0 4.822 4.902 4.763 4.677 4.791
2.0 4.534 4.397 4.172 4.066 4.292
3.0 4.365 4.151 3.899 3.787 4.051
4.0 4.263 4.012 3.748 3.632 3.914
Table 19.
Reliability index for S280 cold-formed thin-walled steel eccentrically-compressed members (Residence).
ρ2 = SWk / SLk ρ1 = (SLk + SWk)/SGk Mean
0.5 1.0 2.0 3.0
0 4.782 4.739 4.588 4.511 4.655
0.5 4.598 4.774 4.727 4.672 4.693
1.0 4.520 4.711 4.704 4.661 4.649
2.0 4.389 4.424 4.296 4.216 4.331
3.0 4.307 4.262 4.091 3.999 4.165
4.0 4.254 4.165 3.974 3.876 4.067
Table 20.
Reliability index for S280 cold-formed thin-walled steel eccentrically-compressed members (Office).
ρ2 = SWk / SLk ρ1 = (SLk + SWk)/SGk Mean
0.5 1.0 2.0 3.0
0 4.954 4.909 4.761 4.686 4.827
0.5 4.748 4.947 4.899 4.845 4.860
1.0 4.635 4.860 4.862 4.822 4.795
2.0 4.462 4.511 4.388 4.310 4.418
3.0 4.360 4.323 4.156 4.065 4.226
4.0 4.295 4.213 4.024 3.928 4.115

7. RESULTS AND DISCUSSION

The reliability index of cold-formed thin-walled steel members as shown in Tables 9-20 shows that the reliability index under office live load is higher than reliability index under residence live load. The S280, S350, LG550 axially- compressed and eccentrically-compressed members can meet the requirements of the target reliability index except grade A, B of LG550 eccentrically-compressed members under a small amount of external load combinations. Considering that the width-to-thickness ratio for grade A, B of LG550 eccentrically-compressed members is beyond the limit of Chinese code, the width-to-thickness ratio of flange was suggested to be less than 60 in cold-formed thin-walled steel structure.

CONCLUSION

The reliability index of cold-formed thin-walled steel compressive members for LG550, S350, S280 was calculated using the improved first-order second-moment method. The calculated results show that the S280, S350, LG550 axially-compressed and eccentrically-compressed lipped channel members can meet the requirements of the target reliability index when the load-carrying capacities of members are estimated using the effective width method considering distortional buckling, and keeping the resistance partial coefficient equal to 1.165. The width-to-thickness ratio of flange met the requirement of Chinese cold-formed steel code. The distortional buckling strength of lipped channel steel members in engineering structures can be calculated using the proposed method in this paper when the width-to-thickness ratio of flange meets the requirement of Chinese cold-formed steel code.

CONSENT FOR PUBLICATION

Not applicable.

CONFLICT OF INTEREST

The author declare no conflict of interest, financial or otherwise.

ACKNOWLEDGEMENTS

The author gratefully acknowledges the financial support provided by the Department of Science and Technology Natural Science Foundation Projects of Jiangxi Province in China (No: 20151BAB206055), National Natural Science Foundation Projects of China (No: 51308277), China Postdoctoral Science Foundation funded project (No: 2016M590382), and Science and Technology Innovation Team Foundation Projects of Jiangxi Province in China (No: 20171BCB19001).

REFERENCES

1 B.W. Schafer, "Local, distortional, and Euler buckling of thin-walled columns", J. Struc. Eng., vol. 128, no. 3, pp. 289-299.
[CrossRef Link] 2 AISI S100-2007, North American Standard for Seismic Design of Cold-formed Steel Structural Systems, Washington, D.C, . 3 G.J. Hancock, "Design for distortional buckling of flexural members", Thin-walled Struc., vol. 27, no. 1, pp. 3-12.
[CrossRef Link] 4 B.W.T.Pekoz Schafer, and T. Pekoz, "Laterally braced cold-formed steel flexural members with edge stiffened flanges", J. Struct. Eng., vol. 125, no. 2, pp. 118-127.
[CrossRef Link] 5 Y.B. Kwon, B.S. Kim, and G.J. Hancock, "Compression tests of high strength cold-formed steel channels with buckling interaction", J. Construct. Steel Res., vol. 65, no. 2, pp. 278-289.
[CrossRef Link] 6 L. Yuanqi, W. Shukun, S. Zuyan, and Y. Xingyou, "Experimental study and load-carrying capacity analysis of high-strength cold-formed thin-walled steel channel column under axial compression", J. Build. Struc., vol. 31, no. 11, pp. 17-25. 7 L. Yuanqi, L. Xiang, S. Zuyan, and Y. Xingyou, "Experimental study and load-carrying capacity analysis of eccentrically-compressed high-strength cold-formed thin-walled steel channel column", J. Build. Struc., vol. 31, no. 11, pp. 26-35. 8 S. Zuyan, L. Yuanqi, and W. Shudong, Experimental research on load-carrying capacities of cold-formed super thin-walled axiallycompressed members with channel section, Report, Tongji University, Shanghai Beststeel Structure Building Co., Ltd.: Shanghai, China 2010 9 S. Zuyan, L. Yuanqi, and W. Shudong, Experimental research on load-carrying capacities of cold-formed super thin-walled eccentrically-compressed members with channel section, Report, Tongji University, Shanghai Beststeel Structure Building Co., Ltd.: Shanghai, China, 2010. 10 S. Yanyong, Experimental investigation on load-carrying capacities of eccentrically-compressed members and self-drilling screw shear connections of cold-formed thin-walled steel structures, M.S. Thesis, Tongji University: Shanghai, China, 2008 11 JGJ227-2011, Technical specification for low-rise cold-formed thin-walled steel buildings, China Architecture and Building Press: Beijing, . 12 L. Yuanqi, S. Zuyan, and W. Lei, "Design reliability analysis of high-strength cold-formed thin-walled steel members with lipped channel sections", J. Build. Struc., vol. 31, no. 11, pp. 36-44. 13 L. Yuanqi, X. Hu, and S. Zuyan, "Design reliability analysis of cold-formed thin-walled steel members with S350 hard-rolled steel sheets", Prog. Steel Build. Struc., vol. 149, no. 6, pp. 21-29. 14 L. Yuanqi, X. Hu, and S. Zuyan, "Design reliability analysis of cold-formed thin-walled steel members with S280 hard-rolled steel sheets", J. Tongji Uni. (Natural Sci.), vol. 40, no. 8, pp. 1154-1162. 15 Y. Xingyou, L. Yuanqi, and S. Zuyan, "Nonlinear distortional-buckling strength estimation of cold-formed thin-walled steel members with lipped channel section", J. Cent. South Uni. (Sci. and Tech.), vol. 46, no. 8, pp. 3067-3074. 16 Y. Xingyou, and L. Yuanqi, "Distortional buckling strength of cold-formed thin-walled steel members with lipped channel section", Eng. Mech., vol. 319, no. 9, pp. 174-181. 17 Y. Xingyou, Distortional buckling behavior and design method of cold-formed thin-walled steel members with opening section, Report, Tongji University: Shanghai, China, 2012. 18 GB50018-2002, Technical code of cold-formed thin-walled steel structure[S], China Architecture and Building Press: Beijing, . 19 M. Zaiming, C. Xueting, and Y. Deyu, Design reliability analysis of thin-walled structures. Report, Taiyuan University of Technology: Taiyuan, China, 1987. 20 M. Zaiming, "Preliminary analysis of resistance variation of thin-walled steel structures", Indust. Const., vol. 7, pp. 30-35. 21 Z. Yitao, Experimental and design method study on cold-formed channel steel columns with section thickness less than 2 mm under axial compression. M.D. Thesis, Xi’an University of Architecture and Technology: Xi’an, China 2008. 22 L. Mingde, H. Dexin, and S. Zhihua, Revision assessment of reliability index of building structures., China Academy of Building Research: Beijing, . 23 GB50018, Technical code of cold-formed steel structure (Draft), China Planning Press: Beijing, . 24 GB50068-2001, Unified standard of reliability design for building structures[S], China Architecture and Building Press: Beijing, .