RESEARCH ARTICLE
Dynamic Reliability Analysis of Mega-Sub Isolation System Under Random Ground Motion
Xiangxiu Li*, Xiaojun Li, Aiwen Liu, Qiumei He
Article Information
Identifiers and Pagination:
Year: 2017Volume: 11
First Page: 822
Last Page: 829
Publisher ID: TOCIEJ-11-822
DOI: 10.2174/1874149501711010822
Article History:
Received Date: 06/07/2017Revision Received Date: 06/09/2017
Acceptance Date: 29/9/2017
Electronic publication date: 31/10/2017
Collection year: 2017

open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: https://creativecommons.org/licenses/by/4.0/legalcode. This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Introduction:
The equation of motion of the mega-sub isolation system is derived in the present study. Then, the parameter optimization of the mega-sub isolation system is studied to illustrate the effects of the damping and stiffness of the isolation devices on the reliability of the system.
Methods:
Moreover, based on the first passage mechanism, the calculation procedure of the dynamic reliability of the system is presented. In this procedure, the story drift of the structure is used as the evaluation.
Results and Conclusion:
Numerical example shows that when the damping ratio of the isolation device is given, the overall reliability of the structure increases at first then decreases with increased frequency ratio, when the frequency ratio is constant, the overall reliability of the structure increases with increased damping ratio. In addition, compared to the aseismic system, the overall reliability of the mega-sub isolation system is significantly improved.
1. INTRODUCTION
For modest-height buildings, the implementation of passive control devices can offer a potential improvement in the structural safety and human comfort. But the structural characteristics in most tall and super tall buildings, such as high shear rigidity, tend to prevent the application of the traditional damping devices. A new method for controlling the response of tall buildings or super tall buildings under severe external loads was first introduced by Feng and Mita [1], i.e. the connections between the mega-building and the substructures were released in a mega-sub structure, but the dampers were not installed between the mega-building and the substructures. Using a simple analytical model, a preliminary investigation of the interaction between the mega-frame and the substructures in suppressing the vibrations of the entire mega-sub structure system was carried out. The results show that the substructures in this structural configuration have a strong TMD (tuned mass damper) function. Subsequently, Chai and Feng [2] improved this configuration and proposed a mega-sub isolation system based on the conventional mega-sub frame, and undertook a study of its dynamic response to random wind load excitations. Recently, some studies about the optimal parameters between the substructure and megastructure have been conducted in order to achieve the best performance. Lan et al. [3] proposed a multifunction mega-sub isolation structure, which has the function of the mass dampers and base isolation as well as damping energy dissipation. Qin et al. [4, 5] and Zhang et al. [6, 7] investigated the control performances of the mega-sub controlled structure with different control strategies. Seismic responses of the mega-sub controlled frame with friction damper were analyzed by Lian et al. [8, 9]. Limazie et al. [10] investigated the dynamical characteristics and controlling performances of the mega-sub controlled structure subjected to strong earthquake motion by designing a reasonable and realistic scaled model.
In this paper, the equation of motion of the mega-sub isolation system is established when the substructures are simplified as multi-degree of freedom system. The parameter optimization of the mega-sub isolation system is studied where the reliability of the system is used as the optimization goal, and the influence of the damping and stiffness of the isolation devices to the reliability of the system has also been studied. Comparative analysis of the dynamic reliability between the mega-sub isolation system and the mega-sub aseismic structure was done based on the first passage mechanism. In this analysis, the story drift of the structure is used as the evaluation. Conclusions obtained in this paper can give some useful suggestions for the design of the mega-sub isolation system. Analysis was conducted using a MATLAB based program in this paper.
2. MEGA-SUB ISOLATION SYSTEM
Fig. (1) shows the form of the mega-sub isolation system. In the mega-sub isolation system, the substructures are connected with the megastructure by isolation devices. Theoretical analysis shows that this system can achieve good performance under seismic excitations. Isolation devices can reduce the earthquake responses of both the substructure and megastructure effectively.
3. ANALYTICAL MODEL AND EQUATIONS OF MOTION OF THE MEGA-SUB ISOLATION SYSTEM
3.1. Analytical Model of the Mega-sub Isolation System
For the analysis purposes, the damping devices are simulated with Kelvin model, which is parallel composed of a spring element to simulate the elastic characteristic and a damping element to simulate the damping characteristic of the isolator. The megastructure and substructures are simplified as a series of lumped-mass model. Fig. (2) shows the simplified analysis model of the mega-sub isolation system.
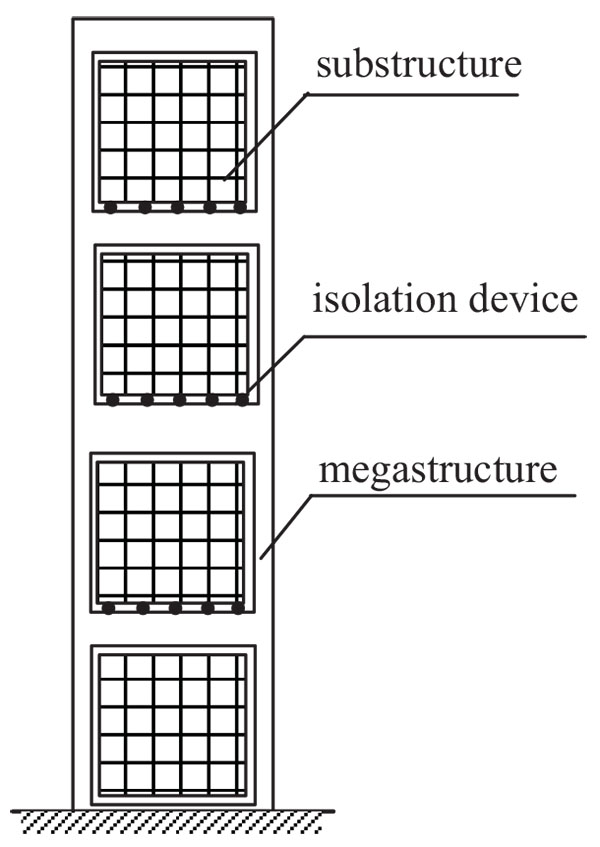 |
Fig. (1). Mega-sub isolation system. |
3.2. Equation of Motion for the Mega-sub Isolation System
According to D'Alembert principle, the equation of motion for the analysis model above can be established as follows:
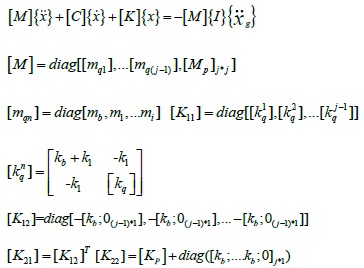 |
(1) |
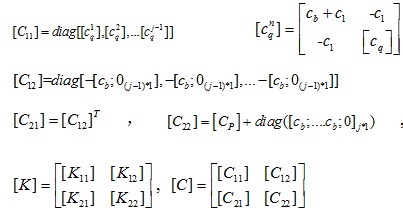 |
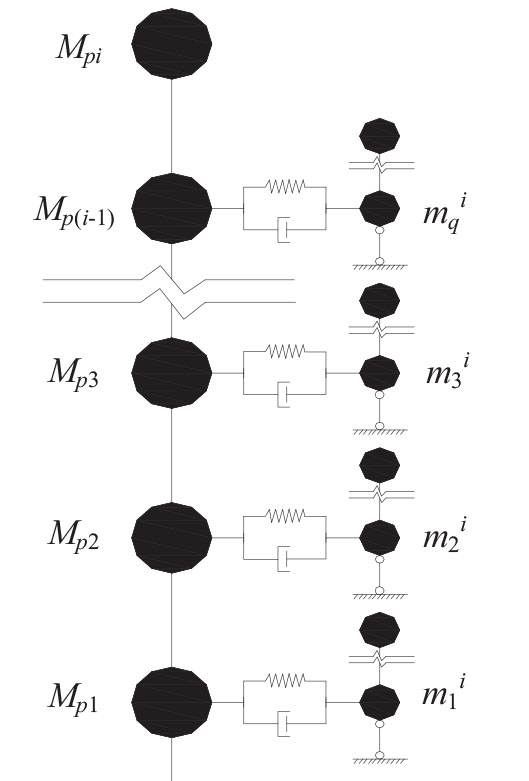 |
Fig. (2). Analysis model of the mega-sub isolation system. |
Where [mqn], is the mass matrix of each group of substructure that is fixed with the megastructure; mi is the equivalent mass of each substructure; mb is the mass of the damping device; [Kq], [Cq] are the stiffness matrix and damping matrix of each group of substructure respectively when the substructures are fixedly connected with the megastructures,
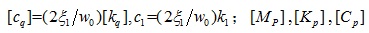 are the lumped mass, Rayleigh viscous damping and shear stiffness of each storey of megastructure respectively; Kb, Cb are the horizontal stiffness and damping of the isolation device,
are the lumped mass, Rayleigh viscous damping and shear stiffness of each storey of megastructure respectively; Kb, Cb are the horizontal stiffness and damping of the isolation device,
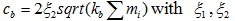 and denoting the damping ratios of the structure and isolation device respectively, and w 0 is the natural frequency of the substructure that is fixed with the megastructure;
and denoting the damping ratios of the structure and isolation device respectively, and w 0 is the natural frequency of the substructure that is fixed with the megastructure;
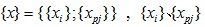 are the relative displacements of the substructure and megastructure respectively with respect to the ground, in which the sub-indexes i and pi represent the storey of substructure and megastructure;
are the relative displacements of the substructure and megastructure respectively with respect to the ground, in which the sub-indexes i and pi represent the storey of substructure and megastructure;
 is the ground motion acceleration.
is the ground motion acceleration.
In order to further analyze the dynamic responses of the system, complex modal theory is used. In this theory, the state variable is introduced, i.e.
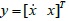 so that Eq. (1) can be transformed in the form of state equations; then the complex eigenvalues and the corresponding mode vectors with respect to the state equations were calculated and using these mode vectors, the station equations can be decoupled. Based on the random vibration theory, the power spectrum density functions of the displacement and velocity responses can be obtained, namely Sx (W) and Sx (W). Their mean squares, then, are expressed as follows:
so that Eq. (1) can be transformed in the form of state equations; then the complex eigenvalues and the corresponding mode vectors with respect to the state equations were calculated and using these mode vectors, the station equations can be decoupled. Based on the random vibration theory, the power spectrum density functions of the displacement and velocity responses can be obtained, namely Sx (W) and Sx (W). Their mean squares, then, are expressed as follows:
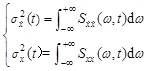 |
(2) |
4. SIMPLIFIED CALCULATION OF STRUCTURAL RELIABILITY
According to the code for seismic design of buildings (GB50011-2010) [11], the deformation failure criteria is used to calculate the anti-collapse reliability, and the ultimate story drift of the structure is taken as the control target, i.e. when the maximum deformation of any layer in the structure reaches the maximum allowable value, the layer is defined as the limit state. In this code, the limit story drift is 1/550rad, and for the isolation layer, the smaller value between the 0.55d (d represents the effective diameter of the isolator) and 3Tr (Tr represents the total thickness of the rubber in the isolator) is taken as the horizontal displacement limit. In the present study, the deformation limit of the isolation layer is selected as 0.55d, and for ease of analysis, the following conversion formula is adopted:
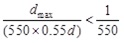 |
(3) |
where d = 800mm, dmax is the maximum deformation of the isolation layer.
Based on the first passage mechanism, the structural reliability can be expressed as:
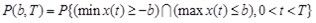 |
(4) |
where P(b,T) is the reliability; x(t) is the structural response; b is the crossing boundary; T is the duration of the ground motion.
For the stationary Gaussian process, the expected rate of the response crossing the boundary b is given by:
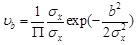 |
(5) |
Where
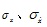 are the variance of the story drift and its derivatives of the i layer respectively, which can be obtained by the method mentioned in 2.2 section.
are the variance of the story drift and its derivatives of the i layer respectively, which can be obtained by the method mentioned in 2.2 section.
When the crossing boundary b is very large, the cross opportunity between the structural response and the boundary becomes very small, which belongs to the rare events. Each cross, then, can be considered as an independent event, and the number cross b in the time interval [0 T ] obeys Poisson distribution. Based on the assumption, the probability of the structural response crossing the boundary b can be represented by:
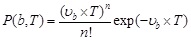 |
(6) |
where n is the total number of the structural response crossing the boundary b in the time interval. Therefore, the dynamic reliability of the structure in the time interval can be defined as the probability of the structural response crossing the boundary b with zero time. Substituting Eq. (5) into Eq. (6) and letting the cross number n being zero, the reliability of the ith layer in the mega-sub isolation system can be derived as follows:
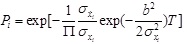 |
(7) |
It is assumed that the whole structure is damaged once the megastructure, substructure or isolation layer is damaged, and the damage between the layers is unrelated with each other. Then the reliability of the mega-sub isolation system can be obtained as:
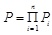 |
(8) |
5. PARAMETER OPTIMIZATION OF MEGA-SUB ISOLATION SYSTEM
The optimization goal in this study is to maximize the reliability of the mega-sub isolation system, i.e.
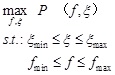 |
(9) |
where fmin, fmax represent the lower and upper limit of the frequency ratio; ξmin, ξmax represent the lower and upper limit of the damping ratio.
Now a typical project was selected as an example [12], which comprises five mega-stories and six-story substructures attached to megastructure from the second floor to the fifth floor. The damping ratio of the megastructure was 0.05. The mass and shear stiffness of each megastructure were 9×105 kg and 9×107 N/m respectively, and the mass of the top megastructure was 4.5×105 kg. The mass of each substructure was determined by the mass ratio u, and each substructure had the same parameter values. When the megastructure was simplified as a series of particle-based model, its first period was 2 sec, and the fundamental period of the whole structure was 2.8 sec when the substructures were rigidly connected with the megastructures. The modified Kanai-Tajimi model suggested by Hu Yuxian [13] was employed as the stochastic ground motion model, and the parameters S 0, wg, ξg and wc were taken as 70.9 cm2/(rad·s3), 17.95rad/s, 0.72 and 3.11rad/s, respectively. In the optimization process, we set fmin = 0.01, fmax =1.5, ξmin =0.01, ξmin =0.25.
The three-dimensional plot and contour plot among the overall reliability of the structure, the frequency ratio and the damping ratio of the isolation layer The three-dimensional plot and contour plot among the structural reliability, the frequency ratio and the damping ratio of the isolation device are shown in Fig. (3) (the mass ratio u is taken as 1.5).
Fig. (4) shows the relationship between the structural reliability and the frequency ratio of the isolation device. It can be seen that for each curve, which represents different damping ratio of the isolation device ranging from 0.01 to 0.25, the structural reliability firstly increased and reached a peak around the frequency ratio 0.51, then decreased with increasing the frequency ratio. Obviously, the frequency ratio corresponding to the peak of the structural reliability was found to be optimal for the isolation device. Fig. (5) shows the relationship between the structural reliability and the damping ratio of the isolation device. It can be seen that for each curve, which represents different frequency ratio of the isolation device ranging from 0.01 to 1.5, the structural reliability increased with increasing the damping ratio. Obviously, the damping ratio corresponding to the peak of the structural reliability was optimal for the isolation device. So the optimal frequency ratio and the optimal damping ratio of the isolation device were observed to be 0.51 and 0.25 when the mass ratio u was taken as 1.5, respectively.
 |
Fig. (3). The three-dimensional plot and contour plot among the overall reliability of the structure, the frequency ratio and the damping ratio of the isolation layer. |
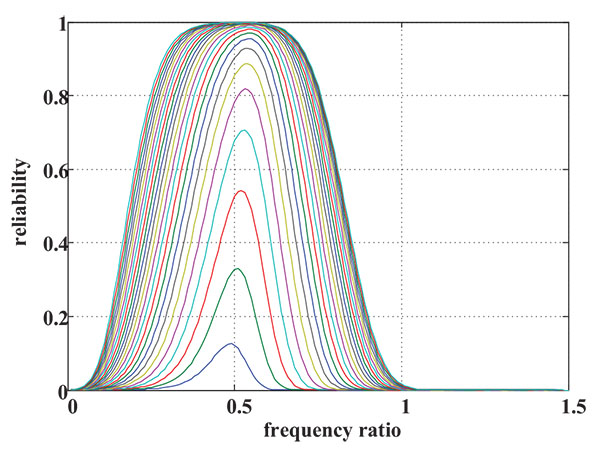 |
Fig. (4). The relationship between the structural reliability and the frequency ratio of the isolation device |
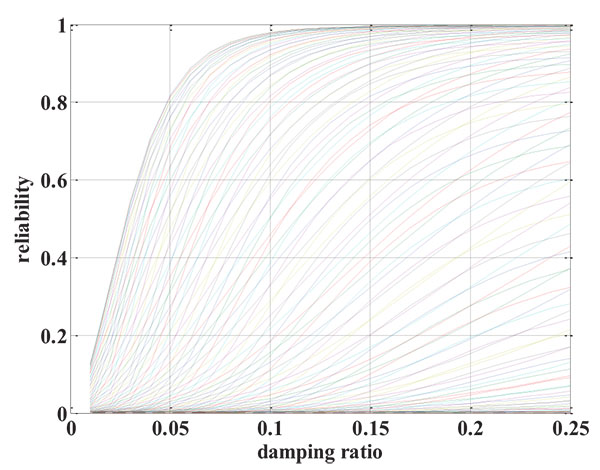 |
Fig. (5). The relationship between the structural reliability and the damping ratio of the isolation device |
6. CALCULATION OF RELIABILITY
Based on the optimal results aforementioned, the frequency ratio and the damping ratio of the isolation device were taken as 0.51 and 0.25 respectively. The obtained reliability of the megastructure and the substructure are illustrated in Tables 1 and 2, respectively. The numbers 1 to 5 in Table 1 represent the floors of the megastructure, the numbers 1 to 6 in Table 2 represent the floors of each substructure, and the first, second, third and fourth in Table 2 represent each six-story substructures that are attached to megastructure from the second floor to the fifth floor.
| Floor | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| Megastructure | Aseismic structure | 0.31 | 0.77 | 0.77 | 0.95 | 1 |
| Isolation structure | 0.99 | 0.99 | 1 | 1 | 1 | |
| Floor | 1 | 2 | 3 | 4 | 5 | 6 | Isolation device | |
|---|---|---|---|---|---|---|---|---|
| First | Aseismic structure | 0.54 | 0.79 | 0.96 | 0.99 | 1 | 1 | — |
| Isolation structure | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| Second | Aseismic structure | 0.94 | 0.98 | 0.99 | 1 | 1 | 1 | — |
| Isolation structure | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| Third | Aseismic structure | 1 | 1 | 1 | 1 | 1 | 1 | — |
| Isolation structure | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| Fourth | Aseismic structure | 0.98 | 0.99 | 1 | 1 | 1 | 1 | — |
| Isolation structure | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
It can be seen that the reliability of the aseismic structure is smaller than that of the isolation structure in the megastructure or the substructure, due to the existence of the isolation devices that provide not only stiffness but also additional damping. It also can be seen that the lower the megastructure or substructure, the larger the failure probability, and this phenomenon exists in both the aseismic structure and the isolation structure.
CONCLUSION
In this paper, the equation of motion for the meg-sub isolation system is established. The calculation method for the dynamic reliability of the system is presented based on the first passage mechanism. In addition, the parameter optimization of the mega-sub isolation system is studied. Several conclusions can be drawn as follows.
When the damping ratio of the isolation device is determined, the overall reliability of the structure increases at first then decreases with increasing the frequency ratio. When the frequency ratio is constant, the overall reliability of the structure increases with increasing the damping ratio.
The reliability of the megastructure and substructure in the aseismic structure is smaller than that in the isolation structure. That is because some isolation devices are placed on the isolation structure, and these damping devices can not only provide stiffness but also offer additional damping to the structure.
The lower the megastructure or substructure, the larger the failure probability, and both the aseismic and isolation structure illustrates this phenomenon.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
This work was supported by the National Science Foundation under Grant No. 51608491, and by Beijing Natural Science Foundation under Grant No. 8174081.







