All published articles of this journal are available on ScienceDirect.
Effect of Prestress Force on Natural Bending Frequency of External Prestressed Steel Beams
Abstract
Introduction:
Natural bending frequencies of externally prestressed steel beam have certain sensitivity to prestress force, so they can be used to find the magnitude of prestress force.
Methods:
To answer the question if the existence of externally prestressed tendons increases or decreases the natural bending frequencies of a simply supported steel beam, the calculating formula for natural frequencies is deduced by using the energy method from the view point of prestress mechanism and further verified by the finite element method. Using this formula of universal property, the influence of prestress force, eccentricity and cross-sectional area of tendons on natural bending frequencies of prestressed steel beam is clearly revealed.
Results and Conclusion:
For external prestressed steel beams with straight tendons, their natural frequencies increase with the eccentricity and cross-sectional area of the prestressed tendon, and the eccentricity has a much larger effect on natural frequencies than the cross-sectional area does. The prestress force has no influence on the oven-order frequencies but decreases the odd-order frequencies. With the increasing order number, the prestress effect is much weaker than the effects caused by the eccentricity and cross-sectional area of the tendon.
1. INTRODUCTION
External prestressing technology cannot only reduce the section size of components, thus reduce steel consumption, but also can improve structural bearing capacity. Therefore, compared with ordinary steel beams, prestressed steel beams have been widely applied for a better economic benefit. However, some dynamic problems need to be investigated further. Prediction of the change in natural vibration frequencies with varying magnitude of prestress force for externally prestressed steel beams (EPSBs) is the one of particular importance, especially when prestressed steel beams are subjected to dynamic excitation, such as earthquake and wind [1]. Moreover, for an existed EPSB, it is hard to gauge its prestress force and therefore to acquire its stress and deformation. However, it is an alternative way to gauge its natural frequency only if the relationship between the natural frequency and the prestress force has already been known [2, 3]. The natural frequency of an in-service EPSB will change when the prestress force changes over
time. It is of great importance in this change over time for structural engineers to ensure safety and serviceability of EPSBs.
The effect of prestress force on the dynamic response of pre- and post- tensioned beams is a widely debated topic. Some argue that the natural bending frequencies (NBFs) of prestressed steel beams tend to be decreased as the magnitude of the prestressing force is increased. This is called the “compression-softening” effect which can be explained by the traditional Euler-Bernouli beam theory [4-7]. Others [8, 9] suggest that NBFs of prestressed steel beams would not be affected by the prestress force. This argument has been pushed forward by Hamed and Frostig [10], who developed a nonlinear kinematic model and concluded that the final equation of motion for the vibration beam system was independent of the prestress force. Fang [11] investigated the second order effect of the external prestress force on the NBFs of a simply supported beam based on the energy method and concluded that external tendons almost did not influence the other frequencies except the first-order frequency. For externally prestressed beams, it is found to be the case in numerous experimental studies conducted that their NBFs tend to be increased as the magnitude of the prestress force [12, 13]. Nevertheless, no mathematical model in predicting this experimental phenomenon is formulated despite some attempts [14-16].
In this study, the calculating formula for natural frequencies of simply supported EPSBs with straight tendons is deduced by using the energy method from the view point of prestress mechanism and verified by the finite element method. The influence of the prestress force, eccentricity and cross-sectional area of tendons on NBFs of prestressed steel beam is revealed.
2. TRADITIONAL THEORETICAL ANALYSIS MODEL AND ITS CORRECTION
The traditional vibration theory takes the prestressed tendons as a pair of constant axial compressive force F at each beam end, as shown in Fig. (1).
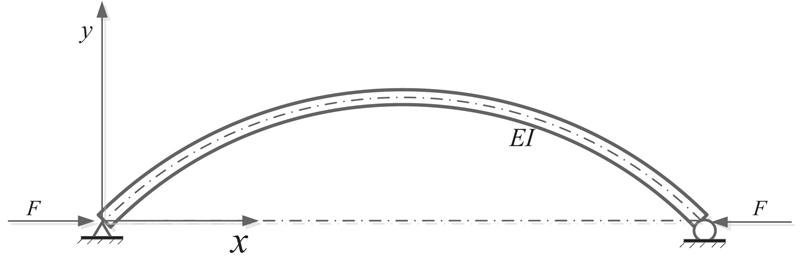
According to the plane-section assumption and neglecting the effects of shear deformation and rotary inertia, the governing partial differential equation of simply supported beam under axial compressive forces for free bending vibration is
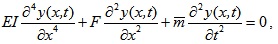 |
(1) |
where E, I, y(x, t) and 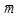 are the elastic modulus, the moment of inertia, deflection of vibration and mass per unit length of the beam, respectively.
are the elastic modulus, the moment of inertia, deflection of vibration and mass per unit length of the beam, respectively.
The NBFs of the beam are
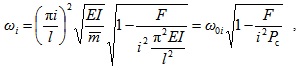 |
(2) |
where the mode number i = 1, 2, 3, …, and l is the length of the beam; the i-th order bending frequency of the beam without axial compression is denoted as ω 0i and the critical Euler force 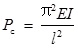 .
.
Equation (2) reveals that the existence of prestress force decreases NBFs of the simply supported beam. However, the experimental phenomenon is contrary to it because the tendon is ignored. Some scholars revised the value of EI in Equation (1) by using experimental data [12]. Although the revised formulas are not exactly the same, they all can be expressed as follows:
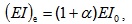 |
(3) |
where (EI)e, α and EI 0 are the revised stiffness of the beam, the modified stiffness factor and stiffness of the beam before revised, respectively. The modified stiffness factor α can be obtained by fitting experimental data, and is still empirical without complete theoretical support, and therefore of no universal applicability.
3. NATURAL FREQUENCY FORMULA OF AN EPSB BASED ON PRESTRESS MECHANISM
3.1. Prestress Mechanism
The mechanism of external prestress systems can be summarized as follows: (1) the prestress causes stress and deformation in the structure and affects its stiffness. (2) The prestressed members, such as tendons, cables and bars, provide additional stiffness for the whole structure as a part of it. There are two ways for them to do so: (a) the axial stiffness of the prestressed member exists itself and is independent of the prestress force; (b) the second-order effect of the axial force imposed by the prestressed members provides stiffness for the structure when the prestressed members generate deformation perpendicular to its axis, which is common in the point-supported curtain walls and the chord-supported structures.
3.2. Natural Frequency Formula for EPSBs with Straight Tendons
Based on three sorts of prestress mechanisms above, the formula for NBFs of an EPSB with straight tendons is deduced by using the energy method. The hypotheses adopted here are consistent with the traditional Euler-Bernoulli bending beam theory. Further, the following three hypotheses are added: (1) the i-th order vibration mode can be expressed as yi = Aisin(iπx / l)sin(ωi t + φi), i = 1,2,3,....., where Ai, ωi and φi are the amplitude, circle frequency and phase angle of the i-th order vibration, respectively; (2) the change of axial force in the tendons is neglected; (3) the axial deformation of the beam imposed by the tendons is also neglected.
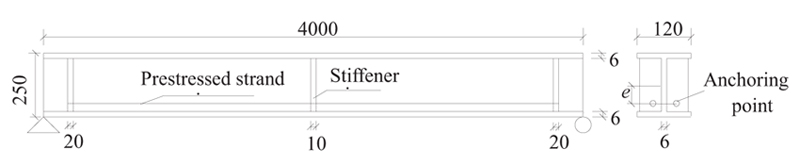
In the straight tendon layout, which is one of the simplest tendon layouts, the prestressed tendon is anchored at both ends of the beam, and the rest of the tendon has no contact with the beam, as shown in Fig. (2), where e is the eccentricity of the prestress force F.
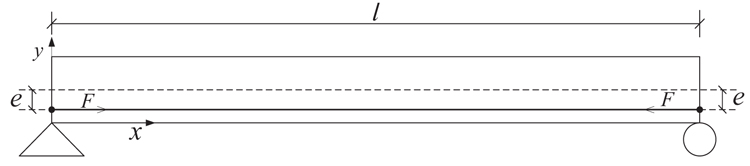
Considering no damping in the process of free vibration of the beam, there is no energy loss. Therefore, the kinetic energy of the beam is always equal to its potential energy. By using modal decomposition, it can be found that for the i-th order vibration,
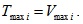 |
(4) |
The potential energy is assumed zero when the beam body is horizontal, and at this position, the kinetic energy of the beam, only considering the beam body, reaches its maximum value Tmaxi. The kinetic energy of the tendons is very small and can be neglected for slight vibration.
The maximum kinetic energy of the prestressed beam of the i-th order vibration is
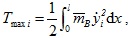 |
(5) |
where 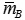 is the unit beam length mass and
is the unit beam length mass and 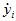 is the vibration speed.
is the vibration speed.
When 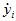 reaches its maximum value, Tmaxi is
reaches its maximum value, Tmaxi is
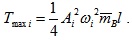 |
(6) |
When the deflection of the beam body is equal to its amplitude, its potential energy reach its maximum value. At this time, the maximum potential energy can be divided into two parts by the prestress mechanism mentioned.
First, according to mechanism 2(a), the stiffness of the tendons, independent of the magnitude of prestress force, is part of the stiffness of the whole structure. For convenience, in small range of deformation, we can substitute the equivalent moment of inertia I' of the beam into its actual moment of inertia considering the contribution of tendons.
From Fig. (3), the equivalent moment is
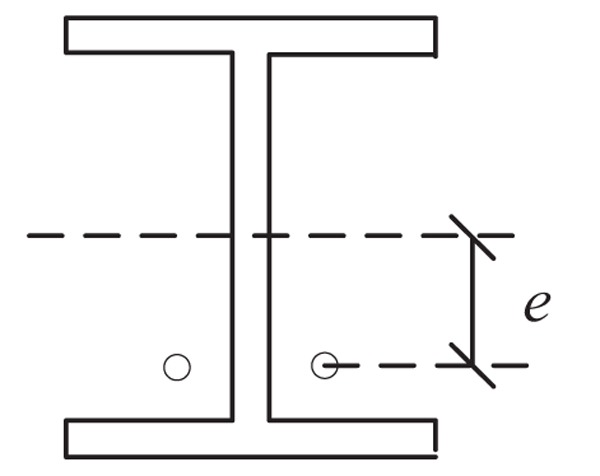
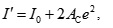 |
(7) |
where I 0 is the actual moment of inertia of the beam and AC is the cross-sectional area of the tendons.
Then the strain energy due to beam bending is
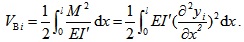 |
(8) |
When the beam deflection reaches its maximum, that is, ymaxi = Ai,
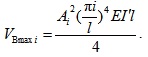 |
(9) |
Secondly, considering mechanism 1, because of beam bending, the tendons are released and its strain energy decreases. The strain energy variation in the tendons is
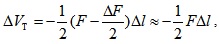 |
(10) |
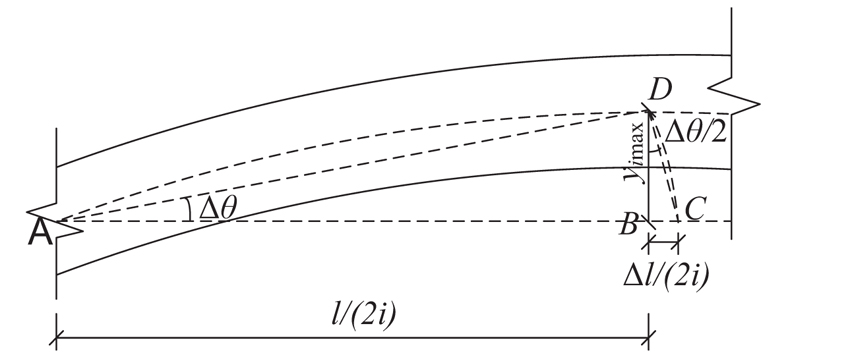
where Δl is the reduced length of the tendons. The reduced length Δl can be found by using Fig. (4), in which arc CD is the trajectory of the middle point of the beam and AD≈AC due to slight free vibration. According to geometric relations,
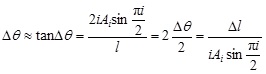 |
Thus,
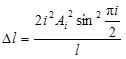 |
(11) |
Substituting Equation (11) into (10) gives
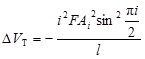 |
(12) |
Substituting Equations (6), (9) and (12) into (4) can find
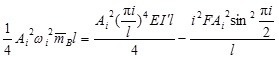 |
(13) |
By solving Equation (13), the i-th order frequency can be expressed as
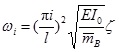 |
(14) |
where the coefficient 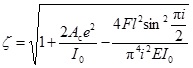 .
.
In the expression of the coefficient ζ, under the square root, the first term “1” represents the NBF of the simply supported beam without tendons. The second term 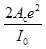 , independent of prestress, denotes the NBF increase due to the tendons. It belongs to mechanism 2(a). For straight tendon layout, the eccentricity has a much larger effect on NBFs than the cross-sectional area does. The third term
, independent of prestress, denotes the NBF increase due to the tendons. It belongs to mechanism 2(a). For straight tendon layout, the eccentricity has a much larger effect on NBFs than the cross-sectional area does. The third term 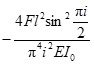 denotes the influence of the prestress on NBFs. It belongs to mechanism 1. For odd-order vibrations, the value of the third term is
denotes the influence of the prestress on NBFs. It belongs to mechanism 1. For odd-order vibrations, the value of the third term is 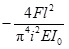 , which means the pretension F decreases the odd-order frequencies. With the increase of i, the prestress effect is much weaker than the effects caused by the eccentricity and the cross-sectional area of the tendons. The absolute value of the third term is less than that of the second one, then ζ > 1, which indicate the effect of tendons. However, for even-order vibrations, the value of the third term is equal to zero, which means the pretension F has no effect on the even-order frequencies for the reason that the length of the tendons remains unchanged during the even-order vibration.
, which means the pretension F decreases the odd-order frequencies. With the increase of i, the prestress effect is much weaker than the effects caused by the eccentricity and the cross-sectional area of the tendons. The absolute value of the third term is less than that of the second one, then ζ > 1, which indicate the effect of tendons. However, for even-order vibrations, the value of the third term is equal to zero, which means the pretension F has no effect on the even-order frequencies for the reason that the length of the tendons remains unchanged during the even-order vibration.
3.3. Influence Factors of NBFs of an EPSB with Straight Tendons
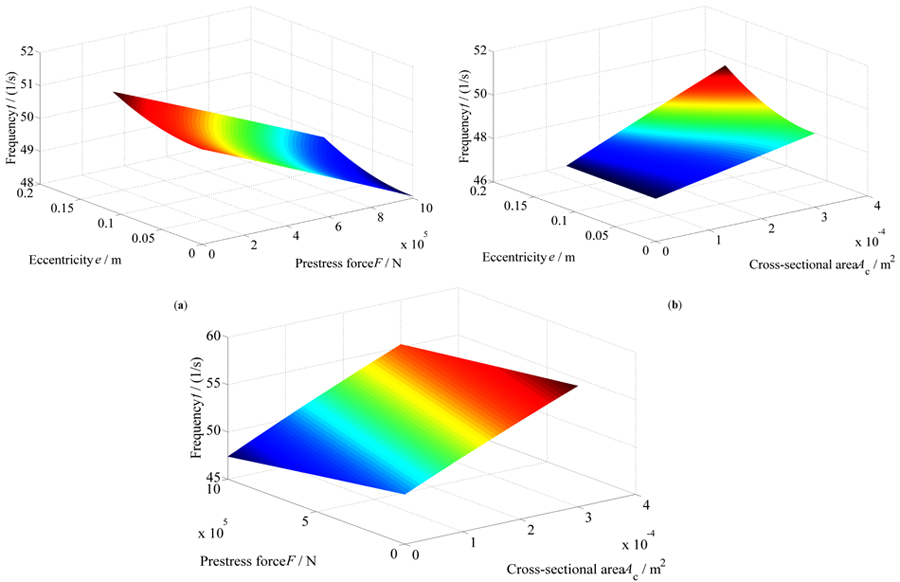
There are three tendon parameters, the prestress F, the eccentricity e and the cross-sectional area of the tendons Ac, which affect the natural frequency f of an EPSB with straight tendons. Because the first-order vibration is usually the most important in practical engineering, only the first-order natural frequency is considered here. Fig. (5) directly reflects their influence on the first-order natural frequency of the EPSB.
4. VERIFICATION BY USING FINITE ELEMENT METHOD
4.1. Finite Element Model for EPSB with Straight Tendons
Finite element simulation is carried out based on the software ANSYS to verify the theoretical formula obtained and find the effect of prestressing on NBFs of EPSBs. Fig. (6) shows the dimensions of an EPSB with straight tendons used for finite element analysis. The stiffeners, placed at the ends and the midspan of the beam body, are added for the convenience of anchoring tendons. The beam body is 4 m in length with the I-section cross section and Chinese Q345 steel. The ϕ15.2 steel strand is used as prestressed tendons. Their material parameters are shown in Table 1.
| Elastic Modulus | Yield Strength | Poisson Ratio | Thermal Expansion Coefficient | |
|---|---|---|---|---|
| Beam | 210 GPa | 345 MPa | 0.3 | 1.2×10-5 /ºC |
| Strand | 190 GPa | 1860 MPa | 0.3 | 1.9×10-5 /ºC |
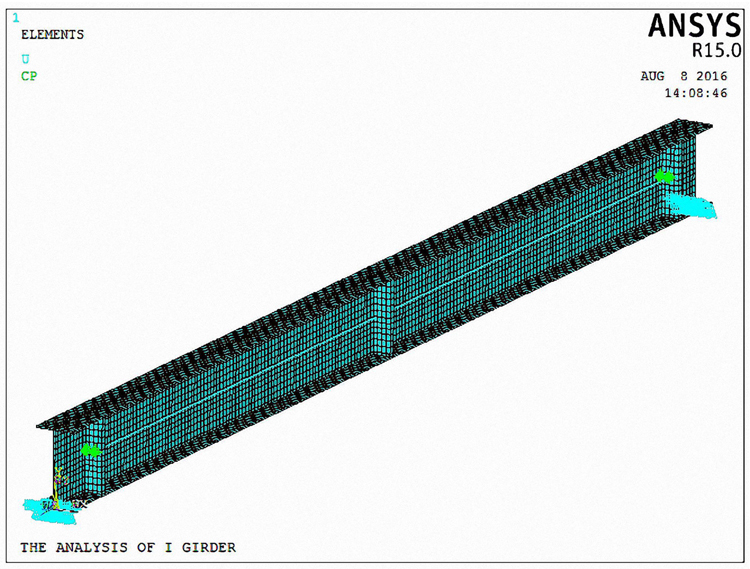
Fig. (7) shows the established finite element model for the EPSB, in which element SOLID 95 is used for the steel beam including the stiffeners. The prestressed tendons are simulated by element LINK 10. The steel beam body and tendons are both meshed based on mapping method. The size of solid elements is about 20 mm × 20 mm × 20 mm.
The anchor of the prestressed tendon and the stiffener of the beam body are regarded as coupling. The tendon can slide through the middle stiffener along the axial direction. Therefore, they can only be coupled with only X and Y degrees of freedom constrained. The prestress is applied by the cooling method.
4.2. Comparison of Theoretical Results with Those by Using Finite Element Method
4.2.1. Influence of Prestress
When the eccentricity of the tendons is 90 mm, the first-order frequencies of the EPSB under different pretension values are listed in Table 2. The first-order frequency of the ESPB obtained by ANSYS decreases gradually with the pretension. When the prestress force increases from 0 to 1000 kN, the simulated and theoretical values of the first-order frequency reduce by 3.44% and 5.29%, respectively. The maximum error of the theoretical values is 1.51% compared with the simulated values.
| Pretension Value (kN) |
Theoretical Value (Hz) |
Change Rate (%) |
Simulated Value (Hz) |
Change Rate (%) |
Relative Error (%) |
|---|---|---|---|---|---|
| 0 | 52.24 | — | 52.02 | — | 0.42 |
| 200 | 51.70 | -1.04 | 51.72 | -0.58 | -0.04 |
| 400 | 51.15 | -2.08 | 51.38 | -1.22 | -0.46 |
| 600 | 50.60 | -3.14 | 51.02 | -1.91 | -0.84 |
| 800 | 50.04 | -4.21 | 50.64 | -2.65 | -1.19 |
| 1000 | 49.47 | -5.29 | 50.23 | -3.44 | -1.51 |
4.2.2. Influence of Eccentricity of Tendon
Different EPSB models with different eccentric arrangements are established under the pretension of 800 kN. The results are listed in Table 3. The first-order frequency of the EPSB increases with the eccentricity. When the eccentricity is equal to 110 mm, the theoretical value increases by 5.99%, and the simulated value increases by 8.23%. When the eccentricity is equal to 70 mm, the maximum error of the theoretical values is 1.74%.
| Eccentricity (mm) |
Theoretical Value (Hz) |
Change Rate (%) |
Simulated Value (Hz) |
Change Rate (%) |
Error (%) |
|---|---|---|---|---|---|
| 0 | 47.97 | — | 47.92 | — | 0.10 |
| 30 | 48.21 | 0.49 | 48.48 | 1.17 | -0.57 |
| 50 | 48.62 | 1.34 | 49.30 | 2.87 | -1.38 |
| 70 | 49.23 | 2.61 | 50.10 | 4.55 | -1.74 |
| 90 | 50.04 | 4.29 | 50.64 | 5.67 | -1.19 |
| 110 | 51.03 | 5.99 | 51.87 | 8.23 | -1.62 |
4.2.3. Influence of Cross-sectional Area of Tendon
The cross-sectional area of the tendon can also affect NBF of the EPSB. The first-order frequencies of the EPSB under different pretension values are listed in Table 4. They increase with the cross-sectional area of the tendon. When the cross-sectional area increases from 54.8 mm2 to 285 mm2, which depends on the specifications of prestressed steel strands, the theoretical value increases by 4.23%, and the simulated value increases by 3.92%. Comparing with the simulated values, the maximum error of the theoretical values is 1.74%.
| Cross-sectional Area (mm2) |
Theoretical Value (Hz) |
Change Rate (%) |
Simulated Value (Hz) |
Change Rate (%) |
Error (%) |
|---|---|---|---|---|---|
| 54.8 | 48.47 | — | 49.29 | — | -1.65 |
| 98.7 | 48.87 | 0.82 | 49.73 | 0.89 | -1.72 |
| 139 | 49.23 | 1.57 | 50.10 | 1.66 | -1.74 |
| 191 | 49.69 | 2.52 | 50.55 | 2.57 | -1.70 |
| 285 | 50.52 | 4.23 | 51.22 | 3.92 | -1.36 |
CONCLUSION
The formula for NBFs of a simply supported EPSB with straight tendons has been developed based on the mechanism of the prestressed system and can accurately reflect the variation of frequency with prestress parameters. It conforms well to the numerical results through the finite element method, and provides a reliable reference for engineering applications.
From this formula, the NBFs of the ESPB with straight tendons increases with the eccentricity and cross-sectional area of the prestressed tendons, and the eccentricity has a much larger effect on NBF than the cross-sectional area does. However, the odd-order frequencies decrease with the prestress force and the prestress force has no influence on the oven-order frequencies. With the increase of the order number, the prestress effect is much weaker than the effects caused by the eccentricity and cross-sectional area of the tendon.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
The research described in this paper was financially supported by the Science Research Program for Key Laboratory of Structure Engineering, Jiangsu Province, China (No. ZD1302), the Jiangsu Qinglan Project, and the MOHURD Project of China (2016-K5-049).


