All published articles of this journal are available on ScienceDirect.
Reliability Analysis Based on Artificial Bee Colony (ABC) and Its Application in Geotechnical Engineering
Abstract
Introduction:
Reliability analysis is a good tool to deal with the uncertainty and has been widely used in the engineering system. The first order reliability method (FORM) is generally used to calculate the reliability index but FORM is time-consuming and requires derivative computing.
Methods:
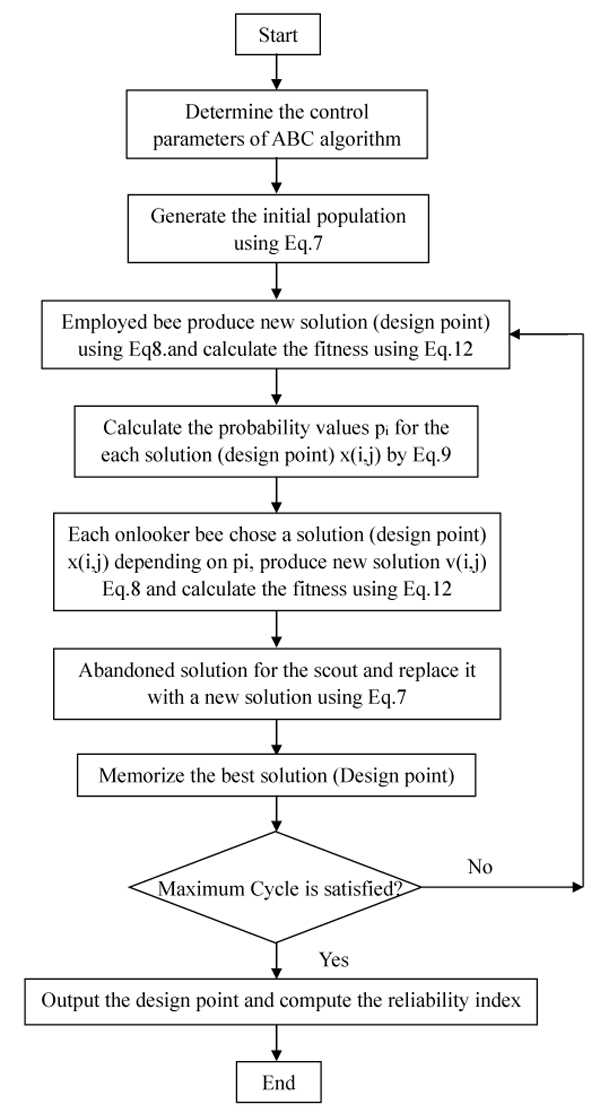
Artificial Bee Colony (ABC) algorithm is a very simple, robust and population-based stochastic optimization algorithm. In this study, an ABC-based reliability analysis was proposed to calculate the reliability index of engineering system through combining Artificial Bee Colony (ABC) algorithm with FORM. FORM was adopted to calculate the reliability index and design point. ABC is used to solve the constrained optimization about FORM. The procedure of ABC-based reliability analysis was presented in detail.
Results and Conclusion:
The proposed method was verified by two classic examples and then applied to geotechnical engineering. The results show that the ABC algorithm can effectively solve the global optimization problem in FORM. Results demonstrate that ABC-based reliability analysis is a good approach to obtain the reliability index and design point with a good accuracy so that it can be applied to analyze the reliability of a complex engineering system.
1. INTRODUCTION
Reliability analysis is a very important method to consider the uncertainty in the engineering system. With the development of reliability theory, reliability analysis has been widely used in engineering system [1-9]. FORM and SORM are generally used to calculate the reliability index and design point [10-14]. However, it requires additional effort for the practical engineering problem due to the implicit form of limit state function. Although Monte Carlo simulation (MCS) can be used to estimate reliability index and the failure probability of engineering system, it is not able to be used to determine the design point and is also a time-consuming approach.
Hasofer and Lind presented a notion of reliability index that can be used to determine the reliability index and design point [14]. To obtain the reliability index and design point, one needs to solve a constrained optimization problem. Abdo and Rackwitz used the Gradient-based method to compute the reliability index [15]. However, it is difficult to compute the derivative of implicit limit state function by this method. The reliability analysis of structures has been described through combining with the generic algorithm and Particle Swarm Optimization (PSO) [2-6]. Artificial Bee Colony (ABC) algorithm simulates the intelligent foraging behavior of honey bee swarms [16]. It is a very simple, robust and population algorithm based stochastic optimization. Sonmez and Kang applied it to structural engineering [17, 18].
The objective of this study is to investigate ABC for reliability analysis. It is organized as follows: FORM and ABC algorithms are presented in Section.2. ABC-based reliability analysis method and the procedure of implementation proposed are presented in detail in Section.3. Two classic examples are used to verify the ABC- based reliability analysis in section 4. In Section 5, the proposed method was used in geotechnical engineering including a finite beam on elastic foundation and a tunnel with rock bolt. Finally, some conclusions are presented. Results show that ABC-based reliability analysis method is effective for the complex engineering system.
2. FORM AND ABC ALGORITHMS
2.1. Form Method
The reliability index is a measurement of the uncertainty of engineering system that takes into account the inherent uncertainty of input variables. The hasofer-lind index is widely used in reliability analysis [14]. The Hasofer-Lind index can be defined as the minimum distance in units of directional standard deviations from the mean-value point of the random variables to the boundary of the limit state surface. The compact form of the Hasofer-Lind index for correlated normal can be expressed as Eq 1:
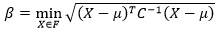 |
(1) |
Where X is a vector representing the set of random variables xi (i=1,2,…,n), μ the vector of mean values; C the covariance matrix; and F is the failure domain.
Low and Tang presented an alternative interpretation of the Hasofer-Lind index based on the perspective of an expanding ellipsoid in the original space of the basic random variables [19], and it was given as Eq 2:
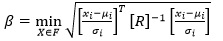 |
(2) |
where R is the correlation matrix; and σi is the standard deviation of random variable xi.
For correlated non-normals, the ellipsoidal perspective remains valid if Eq 3 is expressed as:
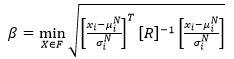 |
(3) |
where μiN and σiN are the equivalent normal mean and equivalent normal standard deviation of random variable xi, respectively.
Based on the reliability index, the probability of failure can be calculated by Eq 4:
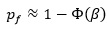 |
(4) |
where Ф() is the cumulative distribution function of the standard normal variable.
To obviate the computations of equivalent normal means and equivalent normal standard deviations, Low and Tang proposed a new efficient algorithm for the FORM by varying dimensionless number ni [19], Eq 5 can be expressed as:
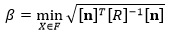 |
(5) |
where n is a column vector of ni (i=1,2,…,m).
When the value of ni is varied during strained optimization, the corresponding value of xi is automatically calculated by Eq 6:
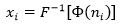 |
(6) |
2.2. Artificial Bee Colony (ABC) Algorithms
The Artificial Bee Colony (ABC) algorithm was originally developed by Karabogain 2005 [16]. In the ABC algorithm, the colony of artificial bees consists of three groups of bees: employed bees, onlooker bees and scouts bees. ABC algorithm requires a cycle of four phases: initialization phase, employed bee phase, onlooker bee phase and scout bee phase.
2.2.1. Initialization Phase
At the first step, the ABC generates a randomly distributed initial population of SN/2 solutions (bees) and calculates the fitness of each solution.
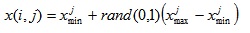 |
(7) |
where x(i,j) is the candidate solution of problem; i = 1, 2,...,SN/2 and SN/2 denotes the size of population; j=1,2, …,D and D is the dimension number of each solution; rand(0,1) is a random number between [0, 1]; ximin and ximax are the upper and lower bound of each solution.
2.2.2. Employed Bee Phase
Once initialization is completed, employed bees search for a solution and calculate the fitness value. A candidate solution can be produced by the memory of bees, which is defined as:
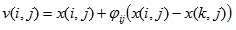 |
(8) |
where k used to be different from, i is the randomly chosen indexes from {1, 2,..., SN/2}, j is also randomly chosen indexes from {1, 2,..., D}, φij is a random number in [-1,1] and controls the generation of neighbor food sources around x(i,j) and represents the comparison of two food positions seen by a bee.
2.2.3. Onlooker Bee Phase
Onlooker bees choose a solution based on the fitness value, determine the solution to be abandoned and allocate its employed bee as scout bees. The probability of being selected for each fitness value, pi can be expressed as:
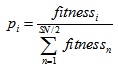 |
(9) |
where fitnessi is the fitness value of the solution.
2.2.4. Scout Bee Phase
In ABC algorithm, scout bees randomly search for a new solution in the determined ranges. The solution that cannot be improved further through a predetermined number of cycles is assumed to be abandoned by onlookers. The abandoned solution x(i,j) is replaced by a new solution x'(i,j) which is the scout bees determined by Equation 11. Each candidate solution v(i,j) produced by x(i,j) can be evaluated using the comparison between x(i,j) and its old solution. The old solution will be replaced by the new solution when it is equal or better than the old solution. Otherwise, the old solution is retained in the memory.
ABC is mainly dependent on three controlling parameters: the number of food sources which is equal to the number of employed or onlooker bees (SN/2), the value of limit (range) and the Maximum Cycle Number (MCN). The procedure of Artificial Bee Colony (ABC) algorithm can be described as follows:
Step 1: Determine the value of control parameters SN/2, MCN and the value of limit for ABC algorithm.
Step 2: Generate the initial population x(i,j) by Eq 7 and evaluate the fitness of each solution.
Step 3: For each employed bee, generate new solution v(i,j) by using Eq 8 and evaluate the fitness.
Step 4: Calculate the probability values pi for the solution x(i,j) by Eq 9.
Step 5: For each onlooker bee, select a solution x(i,j) according to pi, produce new solution v(i,j) and calculate the fitness.
Step 6: If there is an abandoned solution for the scout then replace it with a new solution which will be randomly produced by Eq 8.
Step 7: Trace the best solution.
Step 8: Repeat Step 3 to Step 7 until the maximum cycle number reaches.
3. ABC BASED RELIABILITY ANALYSIS
3.1. ABC-Based Reliability Analysis
Low and Tang proposed a new efficient algorithm for the FORM via varying dimensionless number (Equation 5). According to the FORM algorithm, one has to solve a constrained optimization Eq 10 that is:
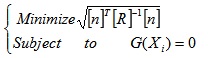 |
(10) |
where G(Xi) is the limit state function. In order to implement ABC to reliability analysis, the above-constrained optimization problem can be changed into the following non-constrained optimization form by penalty method.
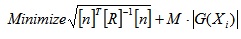 |
(11) |
where M is the penalty coefficient. The choice of the penalty coefficient M is crucial for the convergence and accuracy of Eq 11. In the algorithm of ABC, the fitness function is defined as:
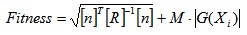 |
(12) |
3.2. The Procedure of Proposed Method
The flowchart of the proposed method is showed in Fig. (1). The algorithm of Low and Tang is used to compute reliability index in this study. Then, ABC algorithm is used to search the design point and determine the reliability index based on fitness function Eq 12.
4. NUMERICAL EXAMPLES
4.1. Example 1
In this section, the serviceability reliability of a cantilever beam with a rectangular cross-section, distributed uniform load and linear elastic behavior is used to verify ABC- reliability analysis. Serviceability failure is considered as an occurrence when the maximum vertical displacement at the free end of the beam exceeds an allowable deflection limit. The allowable maximum deflection of the cantilever beam is defined as L/325, where L is the length of the beam. In this study, suppose the length L and the Young modulus E of the beam have been measured, they are 600 mm and E = 2.6 × 104 MPa, respectively. The limit state function [20] is expressed as Eq 13:
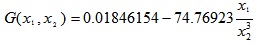 |
(13) |
where x1 and x2 are two independent normal random variables, are the intensity of the distributed uniform load and the height of the beam, respectively. The two variables are subject to independent normal distributions. Their statistical properties are listed in Table 1.
| Variables | Distribution | Mean | Standard Deviation |
|---|---|---|---|
| x1 | Normal | 1000 | 200 |
| x2 | Normal | 250 | 37.5 |
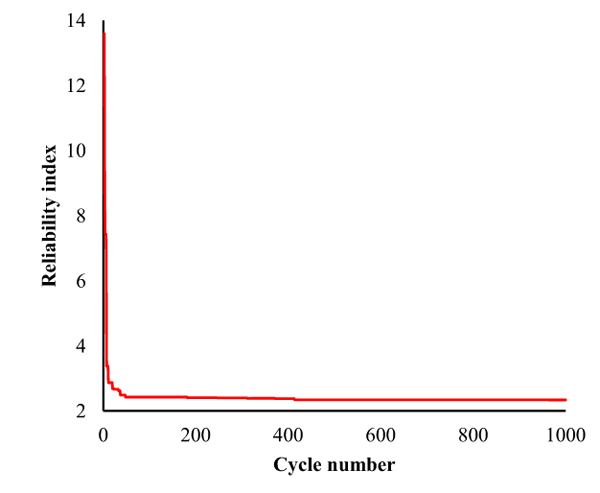
The control parameters SN/2 and the maximum cycle of ABC are 50 and 1000, respectively. The results obtained by the proposed method are shown in Table 2. The failure probability is 0.9607 × 10−2 by using Monte Carlo Simulation [20]. The failure probability obtained by ABC-reliability analysis is 0.9879 × 10−2. The relative error is less than 3%. The reliability index and design points are listed in Table 2 using Excel Solver. The results of the proposed method are in well agreement with the results obtained by Excel Solver. The relationship between reliability index and cycle number is shown in Fig. (2). Fig. (2) shows that the convergence of the proposed method is fast.
| Method | Design Point | Reliability Index | Probability of Failure (10-2) | |
|---|---|---|---|---|
| x1 | x2 | |||
| ABC | 1118.6867 | 165.4704 | 2.3309 | 0.9879 |
| Excel Solver | 1118.5578 | 165.4640 | 2.3309 | 0.9879 |
| Monte Carlo | - | - | - | 0.9607 |
4.2. Example 2
In this section, a nonlinear example [20-22] around design point is used to verify the ABC-reliability analysis. The limit state function is given as:
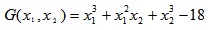 |
(14) |
where x1 and x2 are two independent normal random variables, the parameters of random variables are given in Table 3.
| Variables | Distribution | Mean | Standard Deviation |
|---|---|---|---|
| x1 | Normal | 10 | 5 |
| x2 | Normal | 9.9 | 5 |
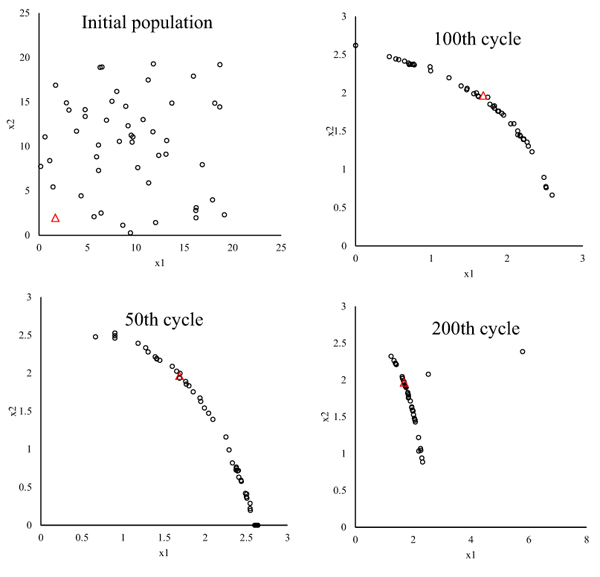
The control parameters of ABC are the same as Example1. The ABC-reliability analysis is used to calculate reliability index and design point, results are listed in Table 4. Fig. (3) shows the variation of design points. The ABC algorithm converges at the 200th cycle. the results are similar to Example1. Results show that ABC-reliability analysis can be used to compute the reliability index and design point.
| Method | Design Point | Reliability Index | |
|---|---|---|---|
| x1 | x2 | ||
| ABC | 1.6944 | 1.9585 | 2.2983 |
| Excel Solver | 1.6856 | 1.9678 | 2.2983 |
5. APPLICATIONS
5.1. Reliability Analysis of Finite Beam on Winkler Medium
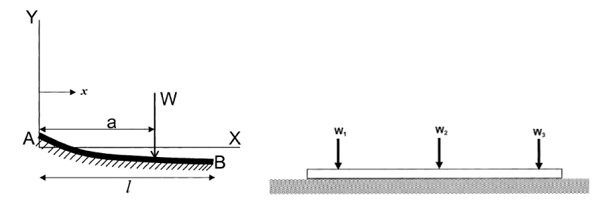
To verify the robustness and accuracy of ABC-based reliability analysis, it was applied to finite beam on elastic foundations with non-normal correlated distribution variables and complex nonlinear limit state function Fig. (4). Beams on elastic foundations can be analyzed using various analytical, numerical simulation [23, 24] and reliability methods. The length and width of the beam are l and b, respectively. The concentrated loads W act at a from the left end of the beam. The bending moment of the beam can be calculated by Eq. 15-25 [24].
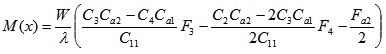 |
(15) |
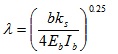 |
(16) |
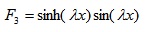 |
(17) |
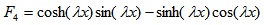 |
(18) |
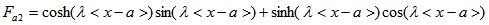 |
(19) |
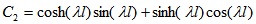 |
(20) |
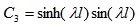 |
(21) |
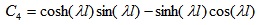 |
(22) |
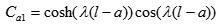 |
(23) |
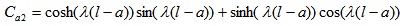 |
(24) |
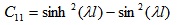 |
(25) |
where Ib is the moment of inertia (in m4) of beam, Eb is Young’s modulus (MN/m2) of the beam, ks is the subgrade modulus (MN/m3), l is the length of beam (in m), x is the distance from the left end of beam, a is the position which load acts from the left end, W is the load.
In this study, the beam is a length of 15 m, a width of 1 m. Three concentrated loads W1, W2, and W3, act at 1.5, 7.5, and 13.5 m from the left end of the beam, respectively. Six random variables are considered: Ib, Eb, ks, W1, W2, and W3. The statistical parameters of random variables are listed in Table 5. Failure is considered to occur if the bending moment reaches 1 MNm anywhere along the beam. For multiple loads W1, W2, and W3, the moment M can be obtained by the superposition method. So, the limit state function is g(x) =1-M.
| Random Variables | Distributions | Para1 | Para 2 | Para 3 | Para 4 | Correlation Matrix | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| W1 | Normal | 0.92 | 0.138 | 1 | 0.8 | 0.8 | 0 | 0 | 0 | ||
| W2 | Lognormal | 1.45 | 0.218 | 0.8 | 1 | 0.6 | 0 | 0 | 0 | ||
| W3 | Extvalue | 0.75 | 0.113 | 0.8 | 0.6 | 1 | 0 | 0 | 0 | ||
| ks | BetaDist | 3 | 3 | 39 | 69 | 0 | 0 | 0 | 1 | 0 | 0 |
| Eb | BetaDist | 3 | 3 | 8000 | 14000 | 0 | 0 | 0 | 0 | 1 | 0 |
| Ib | BetaDist | 3 | 3 | 0.016 | 0.028 | 0 | 0 | 0 | 0 | 0 | 1 |
For BetaDist: Para1,Para2,Para3 and Para4 are α, λ, minimum value and maximum value.
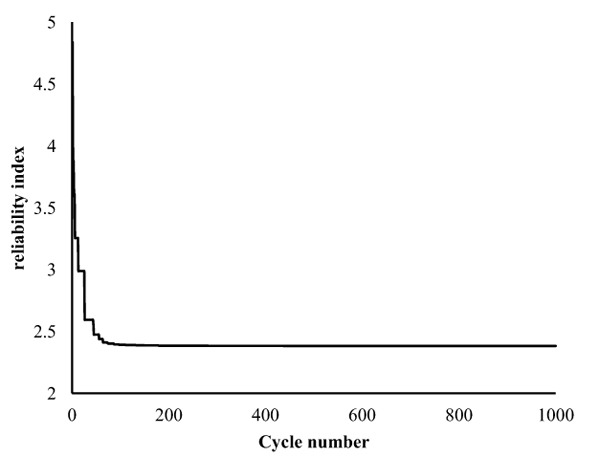
ABC based reliability analysis method was adopted to analyze the finite beam on elastic foundation. The control parameters SN/2 and the maximum cycle of ABC are 50 and 1000, respectively. The proposed method in this study is used to calculate the reliability index and design point (Table 6), the reliability index is 2.3834, which is basically equal to 2.3833 obtained by Excel Solver. The relationship between reliability index and the cycle is shown in Fig. (5). Fig. (6) shows the relationship between fitness value and cycle number. Figs. (5 and 6) show the convergence is quick and ABC-reliability analysis can effectively compute reliability index for the complex, nonlinear limit state function and non-normal and correlated random variables.
| Method | Design Point | Reliability Index | |||||
|---|---|---|---|---|---|---|---|
| W1 | W2 | W3 | ks | Eb | Ib | ||
| ABC | 1.1697 | 2.0297 | 0.9026 | 52.0815 | 11354.5967 | 0.0227 | 2.3834 |
| Excel Solver | 1.1704 | 2.0305 | 0.9038 | 52.1349 | 11343.9948 | 0.0227 | 2.3833 |
5.2. Circular Tunnel with Rock Bolt
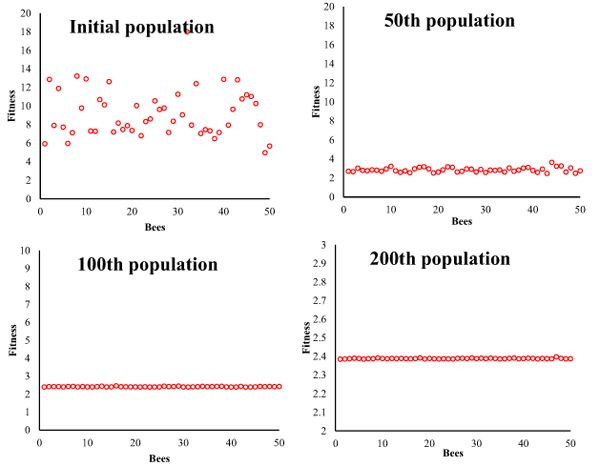
The reliability was evaluated by the proposed method for a radius circular tunnel reinforced by grouted rock bolts. The stability analysis, mechanism of rock bolt and analytical solution are presented in detail by Carranza-Torres [25]. The parameters of tunnel, rock mass and rock bolt are shown in Fig. (7). The elastic modulus (E) of the rock mass the support parameters of rock bolt (rock bolt length (Lb), a distance of rockbolts out of plane(D) and the number of rock bolts) were the random variables (Table 7). The internal pressure pf represents the support provided by the tunnel face at the time the rock bolts are installed. Poisson’s ratio is 0.25. The diameter of all rock bolts is 25 mm; elastic modulus is 210 GPa. The displacement criterion of the tunnel wall was investigated. In this study, the value of εL is taken to be 0.005. So, the limit state function is g(x)=0.005-d (d is the displacement of tunnel wall). The reliability index is 3.1869 based on ABC algorithm (Fig. 7). This is very good agreement with the FORM solution (3.1869). The searching process is shown in Fig. (8).

| Random Variables | Distribution Type | Mean | Standard Deviation |
|---|---|---|---|
| E(Mpa) | Normal | 3200 | 320 |
| Lb(m) | Normal | 5 | 0.5 |
| D(m) | Normal | 2 | 0.2 |
| nb | Normal | 36 | 3.6 |
CONCLUSION
In this study, an ABC-based reliability analysis was proposed and presented in detail based on the characteristic of the simple robust global optimization of ABC algorithm which doesn’t need derivative information of limit state function. Two classic examples were used to verify the proposed method. Results from example 1 and 2 demonstrate that the proposed method can estimate the reliability index and design point with a high accuracy. The proposed approach was then applied two geotechnical engineering problem. Results show that ABC-based reliability analysis can be applied to the complex engineering system with various distribution. Therefore, ABC-based reliability analysis provides a practical approach to reliability analysis of engineering system.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
We gratefully acknowledge financial support from the Program for Innovative Research Team (in Science and Technology) of the University of Henan Province (No.15IRTSTHN029).


