All published articles of this journal are available on ScienceDirect.
Development of Ductile Truss System Using Double Small Buckling-Restrained Braces: Analytical Study
Abstract
Introdution:
This paper proposed a Small Buckling-Restrained Brace (SBRB) for the ductile truss moment frames and is called here as the Double Braced Truss Moment Frames (DB-TMF). The braces are located at the edge of the truss girder and are only placed around the building perimeter. The braces work in pair as a weak element (structural fuses) and is expected to effectively absorb the seismic energy. The proposed DB-TMF system is an extended development of the Knee Braced Truss Moment Frames (KB-TMF). The DB-TMF system is expected to carry the whole seismic loads, while the rest of the frame is designed to carry only the gravity loads.
Methods:
To study the performance of the proposed DB-TMF system, non-linear finite element analysis was carried out using the DRAIN-2DX package. From the analysis with various time history records, it was found that the drift ratio of the DB-TMF system is lower than the allowed story drift. The roof-top displacement shows an asymptotic behavior. The shape of the hysteresis curve tends to have a pinching shape. However, the cumulative ductility of the proposed system satisfies the requirements as a hysteretic structure. In the event of an earthquake, only the SBRB and the chords adjacent to the column element are damaged while the rest of the structural elements remain elastic which is expected.
Results and Conclusion:
Based on the performance evaluation of the DB-TMF system, the DB-TMF system is suitable for moderate seismic region and has smaller dimension steel sections compared to the KB-TMF system.
1. INTRODUCTION
Implementation of the Buckling-Restrained Brace (BRB) as a seismic absorption element or fuse in the high-rise steel structures had shown a significant development. The cross-section of the system consists of a core that has equal capacity for both compression and tension, and a sleeve that works to prevent the core from buckling. Watanabe et al. [1] proposed a rectangular core embedded inside the unbonded materials which was found to be the first work in BRB system. As the BRB system further develops, steel with Low Yield strength (LY) is more preferred as the BRB core material. The strain of the LY steel material can extend up to three times of the A36 steel material. Furthermore, with lower yield strength than the A36 steel material, the BRB elements will yield at a lower seismic load, resulting in a marginal reduction of the overall structural stiffness. Hence, it is expected that the ductility of the structures increases [2-4].
Jia et al. [5] conducted an experimental test to study the behavior of BRB in a structural frame with composite steel-concrete column. It was found that the resulted energy dissipation and ductility of the structural frame with BRB system were higher than a conventional frame without BRB system [5]. However, it was noted that the connection between the beam, column and bracing should be designed to avoid the connection failures. Fahnestock et al. [6] performed some large-scale experimental tests of a frame with BRB system. From the test, the maximum drift ratio of the structures reached 5%. However, it should be noted that when the storey drift reached 2~2.5%, the structural performance was degraded due to the use of rigid beam-column-bracing connection. Qu et al. [7] also conducted an experimental study and proposed a replaceable BRB system which was made of L-shape steel section. From the test, it was observed that the proposed BRB system had a stable hysteretic behavior at a fairly high strain. Other researchers also noted that the use of unbounded BRB system was found to be practical to increase the seismic resistance of the existing and new structures [8]. Furthermore, with a proper placement of BRB element [9], the use of BRB system can reduce the shear force in the shear wall reinforced concrete building. AISC code is usually used to design the BRB element. However, from the experimental test carried out by Chou et al. [10], the AISC prediction of the buckling load of the BRB element [11] was higher than the test result.
Sugihardjo [12, 13] carried out both experimental and numerical investigations of the SBRB system on the Buckling-Restrained Braced Truss Moment Frame (BRB-TMF). In some studies [12, 13], the behavior of the BRB element was modelled using the bilinear stress-strain curve. From the analysis, it was found that the hysteresis curve of the BRB-TMF system showed a fairly stable behavior. However, the rigidity of the hysteresis curve degraded at a higher cycle mode. Nevertheless, the computed total hysteresis energy agrees well with the test result. Wongpakdee et al. [14] proposed a Knee Braced Truss Moment Frame (KB-TMF) using SBRB system which was investigated analytically using the Performed-Based Plastic Design (PBPD). From the analysis, at the collapsed load, it was found that the KB-TMF system was able to be strained up to seven percent. Longo et al. [15] proposed a design procedure for the truss moment frames which ensures that the intended element (BRB) is yielded before the main structural elements.
Sugihardjo and Tavio [16] conducted an experimental test for the SBRB element with a rectangular core. In a study [16], the non-linear finite element analysis was performed using two constitutive laws for the steel material, the elasto-plastic bilinear and the Menegotto-Pinto stress-strain models. From the analysis, it was found that the experimental hysteresis curve is similar to that of the FE model with the steel material modelled using the Menegotto-Pinto stress-strain model. On the other hand, the use of elasto-plastic bilinear stress-strain model showed a compatible cumulative hysteresis energy compared to the test result. From the test result, the hysteresis curve shown a stable behavior up to two percent strain and the cumulative ductility of the SBRB element satisfied the requirements as the hysteresis element.
In this paper, a double SBRB system has been proposed as the ductile elements at both ends of the truss structures and is called as the Double Braced-Truss Moment Frames (DB-TMF). The proposed system is an extended development of the KB-TMF system. KB-TMF system only uses a single bracing [14]. Since the SBRB position on the DB-TMF system may not conform architecturally, the DB-TMF system is only placed around the building perimeter. During the design process, the SBRB element is designed to yield first by increasing the strength of other truss elements with the over strength factor. This way, the other truss elements will remain elastic during the load excitation except for the connection between the chords and the columns [14]. With the design procedure mentioned above, it is expected that the damage in the structural elements occurred in the SBRB elements and the chords adjacent to the columns which are acceptable.
2. MATERIALS AND METHODS
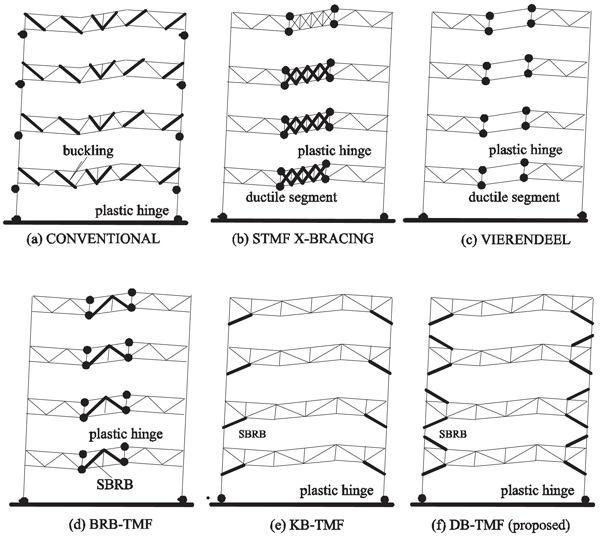
2.1. Conventional and Ductile Truss
Fig. (1) shows the development of conventional Truss Moment Frames (TMF) which has a non-ductile behavior Fig. (1) to a more advanced TMF system which focuses on the ductility and energy absorption of the structures. In the conventional truss system, the failure occurred at the compression diagonal strut, mainly due to buckling. Plastic hinge may also occur at the column. This type of TMF system does not satisfy the Strong Column Weak Beam design philosophy. Previous research also shows that the hysteresis curve is small and is not stable [17]. In Fig. (1), the structural system is called as the Special Truss Moment Frames (STMF). In the STMF system, the seismic energy absorption is carried out by the failure in X-bracing (yielding and buckling) and the plastic hinges that occur at the end of the ductile elements. The STMF structural system can be designed with a seismic reduction factor of seven [11] and the span can extend up to 12 m [18]. In Fig. (1), the truss system is the Vierendeel types. The Vierendeel structural system dissipates the seismic energy via the plastic hinges at both ends of the ductile elements. The advantage of this structural system is the availability of the unused room inside the structures that can be used for plumbing and utilities cables [19]. Fig. (1) shows the BRB-TMF. This system changes the X-bracings with SBRBs [12, 13]. Fig. (1) is the KB-TMF system where the energy dissipation is achieved via single SBRB and plastic hinges at the connection between the chords and columns [14]. Fig. (1) shows the proposed DB-TMF, which uses two SBRB elements that are placed at both ends of the girder. The vertical and diagonal truss elements are connected to the chords using pin connection. The chords itself are designed as beam-column elements.
2.2. Analytical Model for Design and Non-Linear Investigation
To fulfill the main objective of this research, a DB-TMF system of four stories building with seven longitudinal spans is simulated. Fig. (2) shows the plan view and the longitudinal cross section of the buildings. The DB-TMF system is placed only at the perimeter of the building. It is expected that the DB-TMF system carries all seismic load, while the rest of the structures only designed for gravity loads. For design purpose, SAP 2000 [20] is used to analyze and design the required steel section. A response spectrum analysis is used to simulate the applied seismic load to the structure during the design process. On the other hand, to study the inelastic behavior of the designed system, Non-Linear Time History Analysis (NL-THA) according to SNI 1726 [21] is used. From the NL-THA, the performance of the proposed system can be examined and appropriate seismic load reduction factor (R) can be proposed. To maintain equality in the comparisons, the magnitude of the seismic load is adjusted [18].
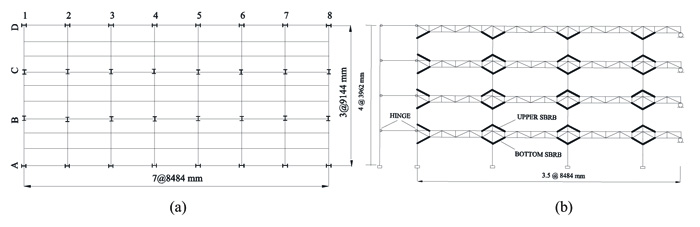
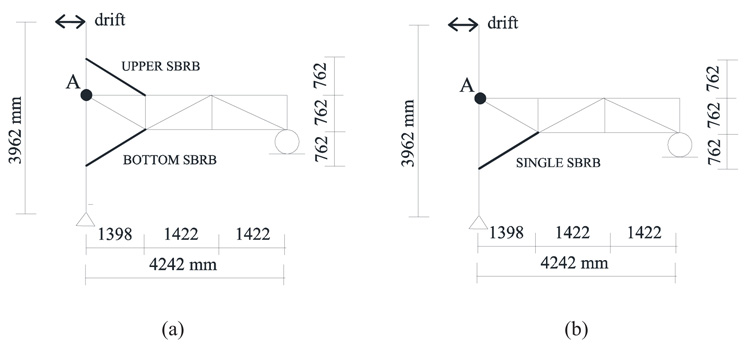
In Fig. (2), the outer left column is a cantilever column with equivalent stiffness of the interior columns in grid B plus C. This column is connected to the DB-TMF system using a rigid link to transfer the given seismic load to the DB-TMF system. SBRBs are placed at both ends of the beam. The inelastic capacity of the SBRBs element is set equal for both compressive and tensile forces. The columns and chords are modelled as a beam-column element while the vertical and diagonal elements are modelled as the plane truss. Once the designed steel section for each element is set as the final, NL-THA of the DB-TMF and nonlinear cyclic load analysis of the simplified TMF systems, as shown in Figs. (2 and 3), are carried out.
By examining the non-linear behavior of the TMF systems, it is possible to compute the cumulative ductility (η) of the structures. This cumulative ductility can be defined as the ratio of the total energy to the elastic energy. A structural system can be said to have the property of hysteresis structure if the value of η is greater than 20 [22]. However, for the SBRB element, the value η must be greater than 100. From the test results [16, 23], the value of η for the SBRB element is usually greater than 100.
Fig. (3) shows the simplified analytical models of the DB-TMF and KB-TMF systems which will be analyzed using the DRAIN-2DX finite element package [24]. The non-linear behavior of the selected TMF system is carried out under cyclic load condition. It should be noted that due to symmetry, only a half span of the structure is modelled as shown in Fig. (3). In the analysis, both the SBRBs element and node A are allowed to yield [14] while the rest of the elements will remain elastic.
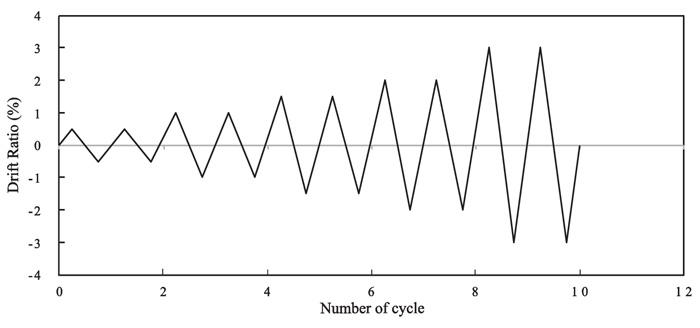
In DRAIN-2DX, the inelastic plane truss element uses the TYPE01 elements while the inelastic beam-column element uses the TYPE02 elements. The TYPE01 element in DRAIN-2DX can undergo yielding in both compression and tension, as well as buckling in compression. The load in Fig. (3) is applied as displacement, based on which, it is computed as the drift ratio from 0.5 up to 3%. The load pattern of the cyclic load is shown in Fig. (4).
3. RESULTS AND DISCUSSION
3.1. Design of Section
The total ultimate dead plus live loads of the structure for each floor is 38.3 kN/m2 which was similar to the value reported in another study [18]. The values for the seismic reduction factor (R) and the importance factor (I) are set to 4.5 and 1.0, respectively. The assumption of using the value for R equal to 4.5 is to study whether the proposed system can at least satisfy the minimum requirements of ordinary truss moment frame system. The parameter of the designed spectral acceleration for short period SDS is set to 0.585 which is similar to the Surabaya city response spectrum with medium soil category. The base shear of the structures is computed as [21]:
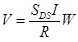 |
(1) |
where W is the total weight of the structure.
By inserting the value of SDS, I and R into Eqn.(1), the total seismic base shear computed was 0.13W which was similar to [18]. All of the structural elements are designed using Bj41 steel material [25] where the yield strength is equal to the A36 steel material. The ratio of inelastic to elastic modulus is assumed to be around 3% [26]. By using the elastic analysis in SAP 2000 [14] and the design code based on SNI 1729 [25], the steel section was designed, and the design results are shown in Table 1.
In Table 1, Columns (1) and (2) show the results of the designed steel section for the DB-TMF and KB-TMF system, respectively. It is worth mentioning that the effective length factor of the KB-TMF columns is larger than the DB-TMF columns. Hence, the designed section of the KB-TMF columns is also larger than the DB-TMF columns. The selection of the core SBRB section must satisfy the requirements of a compact section (b/t < 7.5, [23]). It is shown in Table 1 that the total weight of the KB-TMF system is 8.58 kN which has 19.8% higher weight compared to the proposed DB-TMF system. A rigid assumption between the chords and the column (point A in Fig. (3) was used in the above analysis.
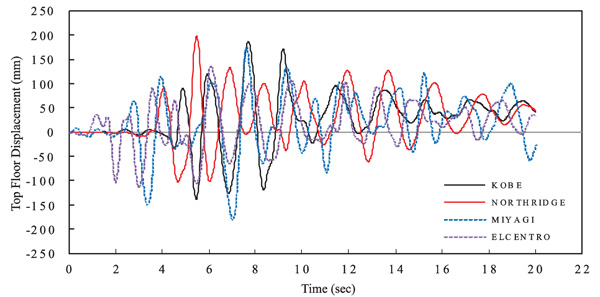
To get the roof-top displacement, the model shown in Fig. (1) was further investigated using the NL-THA which was scaled based on the Surabaya city response spectrum. Fig. (5) shows the results of the scaled Time History response using the available software [27]. The investigated time histories data were Miyagi (1978), Elcentro (1932), Northridge (1984) and Kobe (1985). Using the software [27], the scale factors for each time histories obtained were 0.303, 0.727, 0.280 and 0.244 for Miyagi (1978), Elcentro (1932), Northridge (1984) and Kobe (1985) records, respectively.
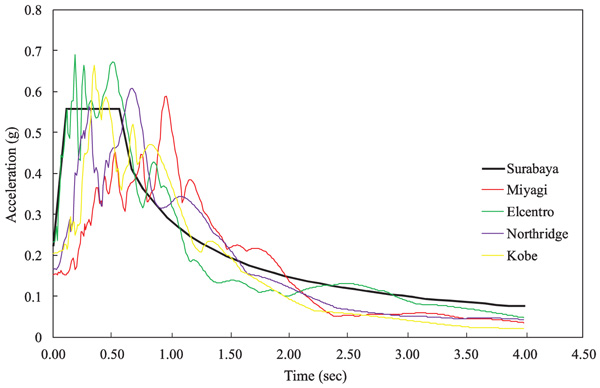
Fig. (6) shows the drift ratios of the DB-TMF system with the selected time history data. In Fig. (6), Miyagi (1978) time history analysis gives the largest structural floor-to-floor displacement. This can be explained because the period of the structure is 1.03 second which is close to the peak acceleration response of the Miyagi time history data (Fig. 5). In Fig. (6), it can be seen that all the drift ratios of the proposed DB-TMF system are still lower than the code maximum threshold which is 2.0%.
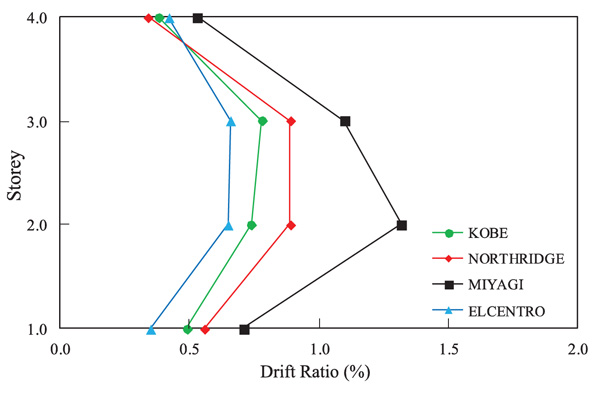
Fig. (7) shows the roof-top displacement for each the carried-out NL-THA. The response of the DB-TMF system is asymptotic which differs from the conventional truss system. In the conventional truss system, the roof-top displacement moves away from the horizontal axis due to excessive unequal yielding in the elements [17].
3.2. Analysis of the Proposed DB-TMF System as a STMF
This section investigates the performance of the proposed model when designed as a STMF with R = 7. Response spectrum analysis with the design spectral response acceleration (SDS) equal to 0.9 (Aceh city) is applied to the structure. The steel sections were designed accordingly which resulted in the DB-TMF-1 system configuration as shown in Table 1 (column 3). As shown in Table 1, all the structural elements of the DB-TMF-1 system had all the section size increased (except the vertical and diagonal trusses) to fulfill the requirement of the STMF system. Using a similar analysis and software [27] in the previous section, the data of time histories were scaled again with respect to Aceh city response spectrum (SDS = 0.9) which gave the scaling parameters for Miyagi, Elcentro, Northridge and Kobe time histories data equal to 0.520, 1.225, 0.478 and 0.415, respectively.
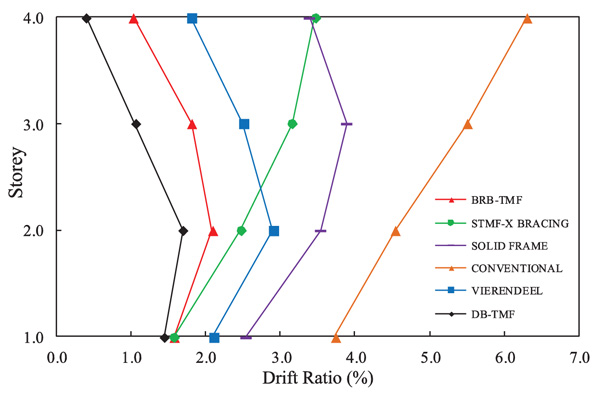
Fig. (8) shows the drift ratios of the proposed DB-TMF-1 system and the other TMF systems with Miyagi time history data. The drift ratio of the proposed DB-TMF-1 system showed a significant reduction compared to the other system such as BRB-TMF [12], conventional truss, solid frames, Vierendeel and STMF [18]. The rooftop displacement behavior of the DB-TMF-1 using the NL-THA with the selected time histories data is shown in Fig. (9). In Fig. (9), there are two earthquakes which restricted the proposed system to achieve the asymptotic behavior and move away from the abscissa. This indicates that the proposed system is not suitable to be used in high-seismic zone despite the smaller drift ratio compared to other STMF system.
3.3. Hysteresis Curve of the DB-TMF
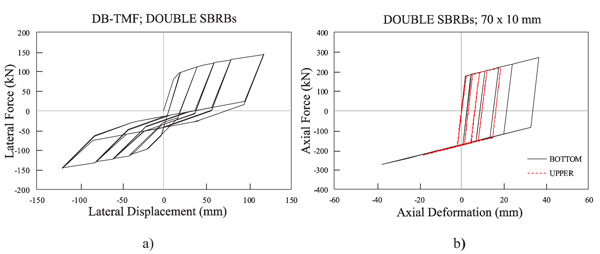
To find out how much energy that can be absorbed by the structural system, in Fig. (3), a displacement cyclic loading pattern is given at the top of the column. The cyclic loading pattern is a function of the drift ratio as shown in Fig. (4) [12, 13, 18]. Fig. (10) shows the hysteresis curve for the DB-TMF system. In Fig. (10), the behavior of the hysteresis curve is pinching, and the stiffness of the system is degraded during reverse loading phase.
The hysteresis curve for the bottom and upper-bracing can be seen in Fig. (10). This figure shows that the maximum axial deformation for the bottom and upper-SBRB reaches 36.88 mm (at axial strain about 2.32%) and 18.55 mm (at axial strain about 1.17%), respectively. The top bracing absorbed lower cyclic load energy which was the primary cause of the stiffness degradation of the DB-TMF system during the reverse loading phase (Fig. 10). Both bracings were not fully functional as the buckling restrained braces because there were no shortening strains in the cyclic responses.
| Component | DB-TMF (1) |
KB-TMF (2) |
DB-TMF-1 (3) |
|---|---|---|---|
| Column (stories 1 and 2) | WF 300×300×10×15 | WF 350×350×16×16 | WF 400×400×15×15 |
| Column (stories 3 and 4) | WF 300×300×12×12 | WF 350×350×10×16 | WF 350×350×10×16 |
| Chords | 2CNP120 | 2CNP120 | 2CNP140 |
| Diagonal | 2CNP80 | 2CNP80 | 2CNP100 |
| Vertical | 2CNP80 | 2CNP80 | 2CNP100 |
| Bottom SBRB | 70×10mm | 70x15 mm | 70x15 mm |
| Upper SBRB | 70×10 mm | - | 70x15 mm |
| Steel weight of a half frame |
7.16 kN | 8.58 kN | - |
3.4. Evaluation of the Hysteresis Curve of the KB-TMF
In a study [14], the performance of the KB-TMF under cyclic load was not determined and it is one of the authors’ interests to evaluate the hysteresis behavior of the KB-TMF [14] under cyclic loads.
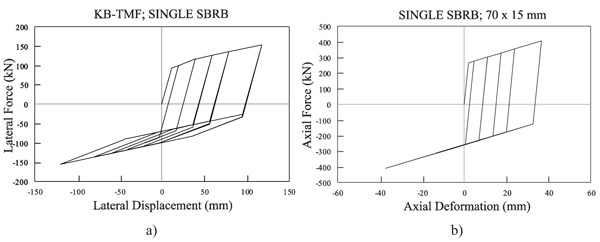
Therefore, in this section, the KB-TMF system is also investigated the same way as DB-TMF system. Fig. (11) and Fig. (11) shows the hysteresis curves for the KB-TMF and single SBRB systems, respectively. Fig. (11) shows that the performance of the KB-TMF system with single bracing is not optimal in carrying cyclic loading. There exists pinching when the load changes from push to pull direction. During the cyclic load excitation, plastic hinge in node A occurred. This finding also agrees well with another research carried out [14]. On the other hand, in the analysis shown in Fig. (11), the performance of single SBRB system is similar with the double SBRB elements (bracing 70 × 10 mm) in DB-TMF systems.
3.5. Hysteresis Energy and Cumulative Ductility
Table 2 shows the hysteresis energy and the cumulative ductility factor η. From Figs. (10 and 11), the cumulative ductility can be calculated. The DB-TMF system has the cumulative ductility of 31.5 greater than the KB-TMF system (η = 27.1, see column (4) in Table 2). This indicates that the DB-TMF system has better hysteresis behavior compared to the KB-TMF system. Both the DB-TMF and KB-TMF systems have a value of η greater than 20 which, in all the systems, satisfies the requirements as a hysteresis structure.
In column (5), for the DB-TMF system, a residual energy of about 12,790 kN-mm (44% of the total energy) is shown which was absorbed by the plastic hinge as a consequence of using the fixed assumption in node A. In the KB-TMF system, the energy absorbed in the plastic hinge was around 11,678 kN-mm (40% of the total energy). This further indicates that node A for both the DB-TMF and KB-TMF systems had relatively large plastic rotation. The bracings for both systems absorbed about 60% of the total energy. From column (4) in Table 2, it can be seen that the value for the cumulative ductility for all type of bracings is still lower than 100. This value of η was observed to be much smaller than the test results which ranged from 199~450 [16].
| Component | Hysteresis Energy ΣWi (kN-mm) (1) |
First Yield Load Py (kN) (2) |
First Yield Displacement dy (mm) (3) |
Cumulative Ductility η (4) |
Energy Absorbed by a Plastic Hinge (kN-mm) (5) |
|---|---|---|---|---|---|
| DB-TMF with a plastic hinge at node A |
29,073 | 81.31 | 11.36 | 31.5 | 12,790 (44%) |
| BOTTOM BRACING 70×10 mm |
11,754 | 178.15 | 1.98 | 33.3 | |
| UPPER BRACING 70×10 mm |
4,529 | 178.15 | 1.98 | 12.8 | |
| KB-TMF with a plastic hinge at node A |
29,216 | 93.12 | 11.56 | 27.1 | 11,678 (40%) |
| SINGLE BRACING 70×15 mm |
17,538 | 266.41 | 1.98 | 33.2 |
CONCLUSION
This paper proposed a Small Buckling-Restrained Brace (SBRB) for the Double Braced-Truss-Moment Resisting Frames (DB-TMF). SAP 2000 finite element package was used to analyze and design the steel section of four stories building. The seismic load used in design was based on the response spectrum analysis. NL-THA was used to study the behavior of the roof-top displacement and the drift ratio of the structure. On the other hand, DRAIN-2DX finite element computer package was used to study the DB-TMF and KB-TMF system under cyclic load. Using the DB-TMF system as the ordinary truss moment frames, the drift ratio with varying time history data shows the drift ratios to be lower than 2% thereby satisfying the code requirements. Compared to the KB-TMF system, the proposed DB-TMF system requires less steel material but has better hysteretic performance. The roof-top displacement of the DB-TMF system which was analyzed in DRAIN-2DX package with several earthquake time histories had shown an asymptotic behavior. The hysteresis curve was shown to be stable with excellent energy absorption which indicates that the proposed structural system (DB-TMF) can absorb moderate seismic load without a significant reduction in its stiffness. It is also worth mentioning that after the seismic excitation, the structural deformation is almost as in the original undeformed state. The elements that yields were the braces and the chords adjacent to the columns while other elements remained elastic. The performance of the DB-TMF system is still lower than other TMF systems such as STMF, Vierendeel and BRB-TMF. Therefore, the proposed DB-TMF system can be categorized as the Ordinary Truss Moment Frames with the value of R equal to 4.5 and can be used as an alternative structural system.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.


