Response Control of Structures with Friction Dampers under Blast Loading

All published articles of this journal are available on ScienceDirect.

RESEARCH ARTICLE

Response Control of Structures with Friction Dampers under Blast Loading

Kupphalli Krishne Gowda Kiran1 Ehsan Noroozinejad Farsangi2 , * Open Modal
Authors Info & Affiliations
The Open Civil Engineering Journal • 27 Aug 2021 • RESEARCH ARTICLE • DOI: 10.2174/1874149502115010244

Abstract

Introduction:

This study investigates the performance of the surface blast load acting on Moment Resistance Frames (MRF)with a novel slip load friction damper. Recently the world is facing terrorist activities that lead to the damage of the structures, including commercial, industrial, and public buildings.

Methods:

These structures should be protected by using control devices. Friction damper is a passive damping device that absorbs maximum energy released during vibrations. Blast loads are calculated based on empirical equations.In this study, single slip and double slip load friction dampers considering the hysteresis loops are used for controlling the response of the MRFs exposed to blast loadings.

Results:

The four storey, eight storey, and twenty storey MRFs with surface blast responses are controlled by using single and double slip load friction dampers. The response includes displacement, accelerations, velocity, storey drift, storey drift ratio, pressure impulse curve, etc. The torsional effect with two dimensions is considered for the high-rise structure as well.

Conclusion:

It was concluded that using friction dampers plays a vital role in controlling the response of MRFsunder blast loadings.

Keywords: Blast load, Pressure impulse curve, MRF, FSDL, FSSL, Storey drift, Storey drift ratio.

1. INTRODUCTION

The performance of the civil structural systems with extreme events such as blast load leads to excessive devastations over the last decade [1]. Extreme terror incidents happened, causing significant devastation to infrastructure system, civil structures, and military camps . The blast resistance design of the structure is needed nowadays because detonations of targeting civil structures and commercial structures occur due to more than 20% of attacks. Hence devastating high-risk structure, military structure, and commercial structure [2].The rapid industrialization's growth leads to both internal and external explosives, hence it is necessary to resist the structure against the blast load [3, 4]. Some of the typical examples of blast load were observed on March 21, 2019, an explosion at a warehouse at Tianjiayi Chemical Co., Ltd., Xiangshui, resulted in 78 died and more than 617 injuries, Tianjin Port of China in August 2015 internal explosives caused a lot of casualties , 5km radius from the center of the explosives structure were all collapsed, on August 4, 2020 at Beirut’s Airport, Lebanon explosive caused to more than 170 casualties [5-9].

The dome structure exposed to blast load is analyzed considering various input parameters of the blast load. The response of the dome structure due to blast load is calculated [10,11]. The numerical simulations and experimental method of the column with FRP retrofitted exposed to blast load were analyzed [12]. The failure mechanism of the beam under blast load is analyzed. The shear demand experienced at the initial stage was calculated [13]. The steel frame building with different configurations are charge weight as an uncertain parameter, detonation location, standoff distance, and column orientation on the fragility of the steel frame buildings under blast load are analyzed [14].The numerical simulations of the perforated steel column with blast load are analyzed by using the FE software of the LS-DYNA [15]. The new numerical method is developed for the analysis the structure exposed to blast wave obtained from the large TNT explosives. The blast wave consists of both air blast load and surface blast load [16]. The response of the RC wall system exposed to both surface and air blast load is analyzed and the construction of the fragility curves are kown to be the failure criteria [17].

The three different floors of RC MRF (Moment Resistance Frame) exposed to blast load are analyzed by using Modal Pushover Analysis (MPA), Non-Linear Response History Analysis (NRHA), and the proposed Multi-mode Adaptative Pushover analysis (MADP) [18]. MRF with steel slit walls exposed to seismic loads is analyzed by using non-linear static analysis [19]. Comparative study of different code provisions is Eurocode, American code is used for the analysis of the seismic response of the MRF [20]. The Linear Time History Analysis (LTHA) by using Eurocode is used for the calculation of the response of the RC MRF with seismic load [21].

The twenty bidirectional ground motion data of the seismic load exposed to thirteen multi-storied RC MRF are analyzed considering the torsional irregularities. The torsional irregularity indices are also calculated by nonlinear analysis. The relations between the torsional irregularity indices and storey drift are derived [22]. Torsional sensitivity effect at different levels due to the seismic force demand and controlling the seismic shear force demand by dual plastic hinge method is carried out [23]. The seismic asymmetrical structure considering the torsional effect is analyzed. The roof displacement response is calculated by construction fragility curves for the known damage levels [24]. Many researchers have calculated the seismic response of the high-rise structure by considering the torsional effects [25-32].

The pressure impulse curve is one of the important input parameters of the blast load. Energy-based is one of the methods used to plot the pressure impulse curve for the structural system exposed to blast load [33]. Elastoplastic beam subjected to pressure impulse loading analyzed. The pressure impulse curve is plotted by considering the negative phase and also contour lines of the structural performance are incorporated [34]. The pressure impulse curve is plotted due to large-scale vented gas explosive occurs in the steel tank [35-38]. The empirical equations are derived for the RC columns exposed to blast load at different damage levels [39].

Friction damper absorbs energy released during the excess of the vibrations [40-43]. The response of structure exposed to seismic load with different intensity is controlled with a double slip load friction damper [44]. Optimum design of friction dampers in steel moment resistance frame with the braced structure is analyzed with seismic load and also cost parameter is also considered [45, 46]. Analysis of the seismic performance of the MRF with rotational friction damper with tendon installed iscarried out [47]. Response of larger span structure exposed to seismic load controlled by using a self-centering steel frame with Intermediate Columns Containing Friction dampers (ICSCF) is studied [48]. Analysis of the seismic performance of the MRF with a Knee Bracing Frame and Friction Damper (KBFD) installed between the column is carried out [49]. Analytical and experimental methods were conducted on the structural frame exposed to different loading rates with friction damper [50,51].

Currently, analyzed, designed, and dynamically tested are more advanced friction devices. Some of them are: (i) Self-Centring Frictional Damper (SCFD) [52], (ii) Self-Centring Rotational frictional damper (SCRF) [53], (iii) Excellent performance for the low-rise structure with seismic load by using Self-centring energy-absorbing rocking core system with friction spring damper (SCENARIO) [54], (iv) novel Passive Variable Friction damper (PVFD) [55], (v) novel deformation-Amplified SMA-Friction Damper (DASMAFD) [56], (vi) Dual Self-Centring Variable Friction Damper (DSC-VFD) [57]. Many researcher’s analysis was carried out on the performance of the MRF with rotational friction damper [58-62].

In the gaps of the literature survey, the objectives for the present study are: (i) Response of the MRF with surface blast load is controlled by using Frame with Single Slip Load (FSSL) & Frame with Double Slip Load (FSDL) is compared, (ii) Torsional effect on high rise structure is considered. Simulations have been carried out using the MATLAB platform and the results indicated the accuracy and efficiency of the proposed novel friction damper with single and double slip load friction damper [63-65].

2. MATERIALS AND METHODS

2.1. Blast Load

Two different stages are involved in the analysis of the structure with blast load. The first stage is the calculations of the peak reflected pressure obtained from the time history values of the blast load and the second stage is the calculations of the blast force at each floor of the joint from converting the blast pressure on the area of the joint and results in the performance analysis of the structure. The following equations are used to calculate the blast pressure acting on the frame [14],

(1) (2)

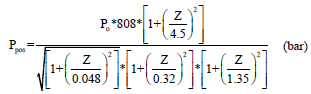
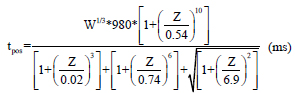
where Ppos - peak incident pressure, tpos- positive phase duration, Po – Peak positive pressure, W - charge weight presented in terms of the mass of the equivalent Trinitrotoluene (TNT) in kilograms, Z - scaled distance expressed as

(3)

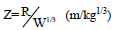
where R= Radial distance in meter, W = Charge weight in terms of the equivalent mass of TNT, pressure wave exerted from the blast load with respect to any time can be expressed as follows

(4)

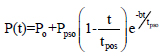
where t = time measured after tA; and b = unitless wave decay parameter

(5)

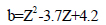
The peak reflected pressure can be computed using the coefficient of reflection (Cr)

(6)

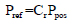
2.2. Torsion

For the high-rise frame structure exposed to wind load, unsymmetrical structure leads to torsional effect. The torsional irregularity indices considering due to eccentricity along X and Y directions expressions are as follows

(7) (8)

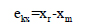
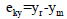
where ekx - eccentricity along the x-direction, eky - eccentricity along the y-direction, (Xm, ym) and (Xr, yr) are the coordinates of the center of mass and center of rigidity respectively.

(9) (10)

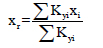
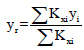
where Kxi and Kyi and are the lateral stiffness of column i along with the global X and Y directions. (Xi, yi) represents the coordinate of column i of the relative reference frame.

Torsional radius along X and Y directions are calculated by using the following equations

(11) (12)

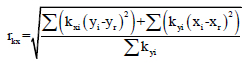
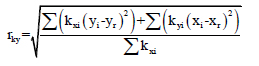
The torsional radius of gyration of a particular floor is given below

(13)

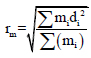
where mi is the lumped mass at a radial distance di from the Center of Mass (CM).

The aspect ratio and stiffness ratio along two-directional are shown below

(14) (15)

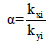
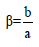
where b and a are the width of the frame along x and y directions respectively. M is the center of mass, mass of the moment of inertial are shown below

(16)

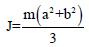
The torsional relative effect index is calculated below ϕ&r are the torsional angle and radius of gyration of the floor, u is the centroid displacement. 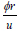is the torsional index which gives the relationship between structural torsion and structural translation

(17)

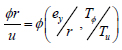
where 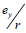represents the eccentricity ratio along the direction Y and 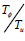is the uncoupled translations torsion period ratio.

2.3. Pressure Impulse Curve

The pressure impulse curve is the important response of the MRF with blast load. Pressure impulse curves are calculated by different energy-based methods, analytical methods, experimental methods. Energy-based method is a simple and accurate method for obtaining the pressure impulse curve. The following equations represent the procedure of plotting the pressure impulse curve [63].

(18) (19)

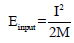
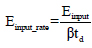
where I – Impulse, β - load pulse shape factor = 0.5 for triangular load, Einput – represents the input energy and Einput_rate - Input energy rate. The dimensionless terms for the two axes are defined as follows

(20) (21)

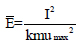
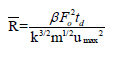
where 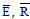represents the pressure and impulse of the curve

2.4. Single Slip Load (SSL) Friction Damper

Fig. (1) represents the hysteretic behaviour of the friction damper of the single slip load. The friction coefficients in their interface and force clamping of moving parts are the parameters depending on single slip load capacity. The slip load can be expressed as

(22)

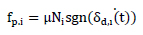
Where fp,I is the passive load, Ni is the constant, preloaded clamping force, µ is the friction coefficient, and sgr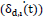 indicates the direction of motion.

(23)

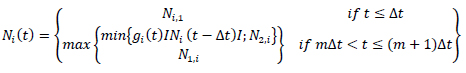
where m=1,2, 3…., n (i.e.∆t is the time at the end of every interval of decision) and Ni (t - ∆t) is the clamping force.

2.5. Double Slip Load (SSL) Friction Damper

Fig. (2) shows the hysteresis behavior of the DSL (double slip load) damper. The axial force of the brace element equals P1, which is known as the first slip load. The maximum amount of first slippage is ∆. The first slippage will be 0.5-time ∆. The axial force of the brace element will be larger when the blast load input reaches the maximum, then the force of the brace element reaches P2 is known as the second slip load.

Fig. (1). Hysteretic behaviour of the friction damper of single slip load.
Fig. (2). Hysteresis loop of the DSL damper.
Fig. (3). Flow chart of the incremental sub-step of the analysis of software in the control force.

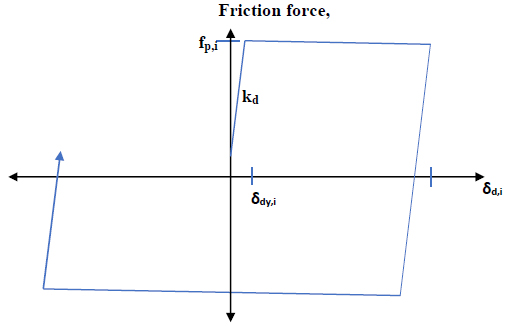
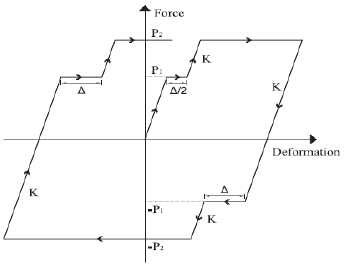
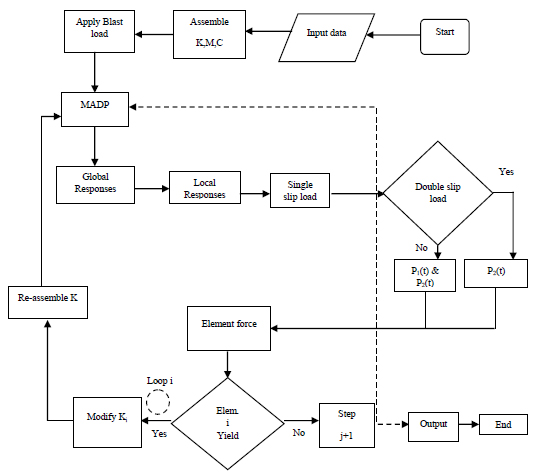
Fig. (3) shows the flow chart of software analysis to obtain the control force in the MRF by single slip load damper and double slip load damper. The assemble of the structural model is created includes stiffness, mass, and stiffness, then apply blast load in terms of the pressure-time curve. The response is calculated by using the Multi adaptative pushover analysis. The responses are local and global responses are calculated. The control force exerted by the single slip load is applied to the frame, if the response from the frame exceeds the limit double slip load damper exerts the force. In the double slip damper, if the force exerted is to control the response of the frame is sufficient then the slip load P2 is sufficient. But, if the double slip damper force is not sufficient then two slip load acts, that is P1 and P2. The force exerted by the damper to the frame is sufficient to control the response otherwise modifies the stiffness. The double slip load damper works on the principle of the hysteresis loop.

2.6. Modelling System with Blast Load

2.6.1. Modelling of the System with Blast Load

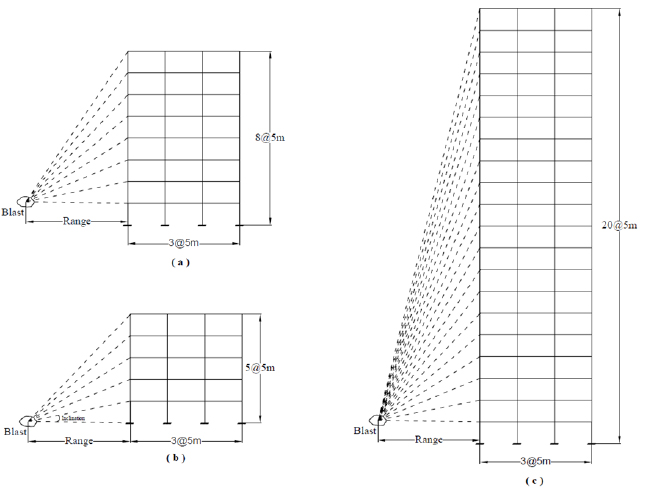
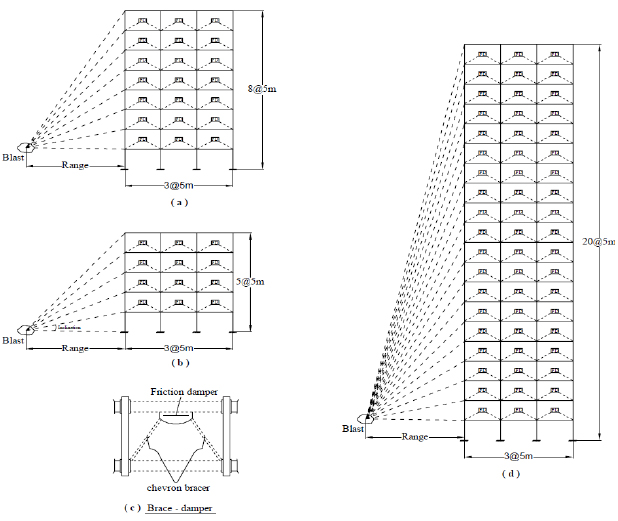
Fig. (4) shows the MRF exposed to blast load. It consists of the three frames that is low rise, mid-rise, and high-rise frames of the 4 storey, 8 storey and 20 storey frames. Each frame has three bays of each bay as 5m, height of each floor is 5m.

The vibration properties, frame properties, and weight in each floor are used in the study as shown in Tables 1, 2 and 3 respectively.

Table 1.
Vibrational properties of the structural frames.
Frame Period (sec) Effective Modal Mass (%)
Mode 1 Mode 2 Mode 3 Mode 4 Mode 1 Mode 2 Mode 3 Mode 4
5 Story 1.09 0.38 0.21 0.13 79.41 12.47 3.96 3.27
8 Story 1.42 0.56 0.23 0.23 73.5 12.65 5.25 2.15
20 Story 1.93 0.72 0.42 0.35 70.69 12.54 4.76 2.92
Table 2.
Frame properties.
MRF Floor Mass
(103 kg) 		Stiffness
(kN/m) 		Damping
(kNs/m)
5-Storey 1 21.213 31860 2100
2 21.213 31860 2100
3 21.213 31860 2100
4 21.213 31860 2100
5 21.213 31860 2100
8-Storey 1 21.213 31860 2100
2 21.213 31860 2100
3 21.213 31860 2100
4 21.213 31860 2100
5 21.213 31860 2100
6 21.213 31860 2100
7 21.213 31860 2100
8 21.213 31860 2100
20-Storey 1 2041 172255 27318
2 2011 156541 24826
3 2011 131956 20927
4 2011 119869 19010
5 2011 111175 17631
6 2011 102413 16241
7 2011 913068 14480
8 2011 818123 12974
9 2011 761873 12082
10 2011 713378 11313
11 2011 668616 10603
12 2011 622953 9879
13 2011 560090 8882
14 2011 512098 8121
15 2011 473719 7513
16 2011 436525 6923
17 2011 398817 6325
18 2011 359101 5695
19 2011 315938 5010
20 2011 271092 4299
Fig. (4). The moment resistance structural frame with blast load (a) 8-Storey (b) 5-Storey (c) 20-Storey.
Table 3.
Weight of the MRF frame.
Sl No Load on the Floor Magnitude
1 Dead load on intermediate floor 600 kg/cm2
2 Live load on intermediate floor 250 kg/cm2
3 Dead load on roof 550 kg/cm2
4 Live load on roof 150 kg/cm2
5 Steel Yield stress 2400 kg/cm2

Table 4.
Bilinear behaviour for steel frame assigned in MATLAB software.
Sl No Parameter Value
1 Yielding stress Fy 235.36 MPa
2 Modulus of Elasticity 205.94 GPa
3 Strain hardening 3%
4 Initial stiffness Plasticity
5 Base condition Fixed

2.6.2. Blast Load Modeling of the System

Surface blast load acting on the frame is analyzed. The pressure is calculated in the above sections. The behaviour of the steel frames and blast load parameters are shown in Tables 4 and 5.

Table 5.
Blast load parameters.
Sl No Parameter Symbol Magnitude
1 Weight W 2000 TNT(Trinitrotoluene)*
2 Range R 10m
3 Scaled Distance Z 0.793 m/kg1/3
4 Peak positive pressure Pso 78.3 kPa
5 Time of arrival tα 81 sec
6 Length of wave Lw 20 m
7 Negative phase durations to 25 sec
8 Positive impulse is 135 kPa -sec
9 Peak reflected pressure Pr 221 kPa
10 Reflected impulse ir 221 kPa sec
* TNT generates blast energy of about 4680 joules per gram (J/g).

2.6.3. Friction Damper with MRF

Friction dampers are installed in each floor as shown in Fig. (5). Table 6 shows the response parameter of the MRF.

Fig. (5). The moment resistance structural frame with friction damper exposed to blast load (a) 8-Storey (b)5-Storey (c) Brace Damper (d) 20- Storey.
Table 6.
Indices J1 to J5 for assessment of control performance.
Sl No Parameter Equation Variables
1 Drift ratio 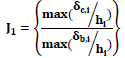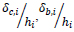= Drift ratio at level i, for controlled
2 Acceleration 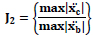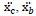= acceleration relative to the ground and control
3 Base shear 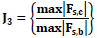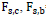= Shear force at the base of the frame
4 Average Drift 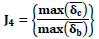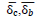= Average of simultaneous drift in the building at time of maximum drift of level i.

The governing equation of motion for n-degrees of freedom-controlled frame subject to blast load can be written as

(24)

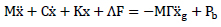
where x is the displacement vector, 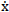and 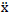represents the first and second time derivatives of x, respectively;F= [fd1,fd2,……..fdn]T and 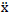g are control force vector and the acceleration due to blast load, respectively; M,C and K are mass, damping, and stiffness matrices respectively; 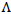is a mass of zeros and ones, where one will indicate the damped force being applied and 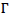is the influence coefficient vector and Pb is the pressure exerted due to blast load.

Equation (xx) can be further transformed to state-space representation as:

(25)

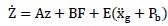
where z is the state vector of structure and contains the relative of ground displacement and velocity of each floor; A denotes the system matrix composed of structure mass, damping, and stiffness matrices; B represents the distributing matrices of control forces; and E represents the distributing matrices for excitation.

(26)

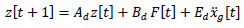
where t denotes the time step; Ad =eAΔt represents the discrete-time system matrix with Δt as the time interval. The constant-coefficient matrices Bd and Ed are discrete-time counterparts of the matrices B and E that may be written as

(27) (28)

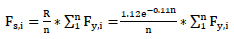
where R is the optimum slip load ratio; n is the number of floor and Fs,i and Fy,i is slip load and shear strength.

The average slip load ratio is obtained from the following equations

(29)

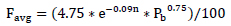
where Favgis the average slip load ratio.

3. RESULTS AND DISCUSSIONS

3.1. Five Storey Frame

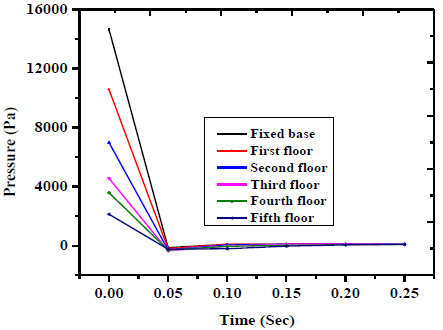
Fig. (6) shows the blast load acting on the five-storey frame. The maximum pressure occurs of 15 kPa at fixed base and the minimum pressure occurs of 2 kPa at the fifth floor.

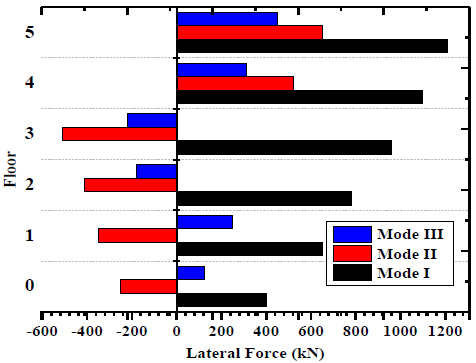
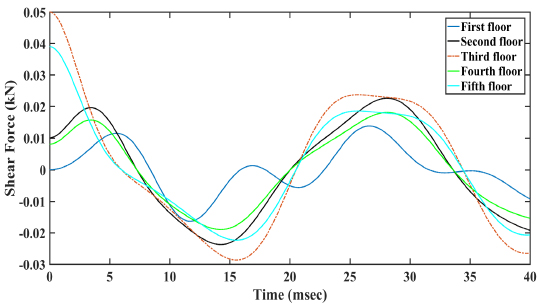
The lateral force occurs at -500 kN to 1200 kN. Fig. (7) shows the shear force acting on the five-storey frame. The maximum shear force occurs of 0.05kN at the third floor and the minimum shear force occurs at 0.01 kN at the first floor.

Fig. (6). Blast load on Five storey frame.
Fig. (7). Lateral Force acting on Five storey frame.
Fig. (8). Shear Force acting on Five storey frame.
Fig. (9). Reduction of response on Five storey frame by using friction damper.
Table 7.
Reductions of the response of the five storey for FSSL and FSDL system.
Sl.No Storey Component Bare FSSL FSDL
1 Fixed Base Accleration (m/sec2) 5.3 4.0 3.9
2 Velocity (m/sec) 4 3.25 2.8
3 Displacement (m) 0.09 0.075 0.05
4 Fifth Floor Accleration (m/sec2) 1 0.8 0.75
5 Velocity (m/sec) 0.5 0.45 0.42
6 Displacement (m) 0.03 0.025 0.022

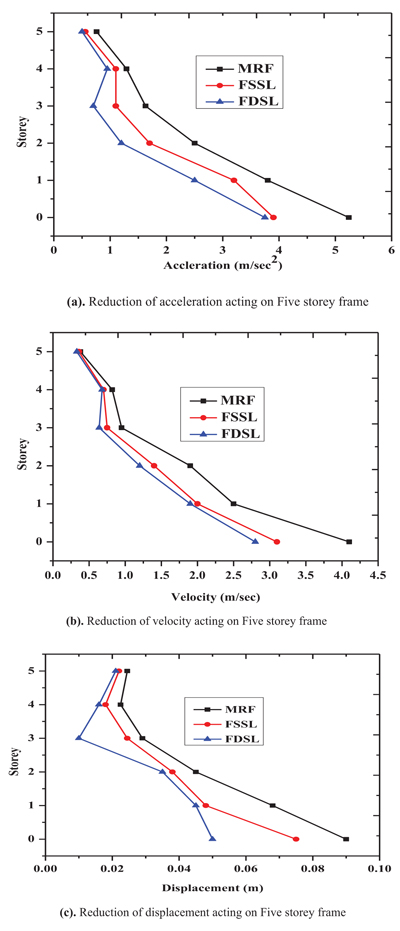
Fig. (9) shows the reduction of the response of five storey structure by using friction dampers.

Figs. (10 and 11) show the increase of the pressure impulse curve in 2D and 3D of five storey frame by using single and double friction damper.

Fig. (10). 2D Increase of pressure impulse on Five storey frame by using friction damper.
Fig. (11). 3D Increase of pressure impulse on Five storey frame by using friction damper.

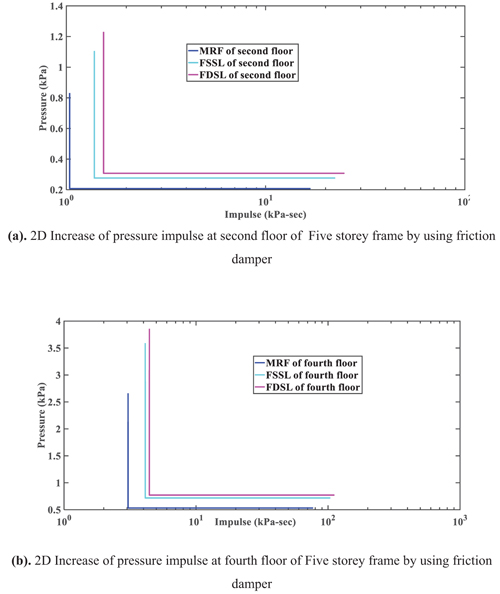
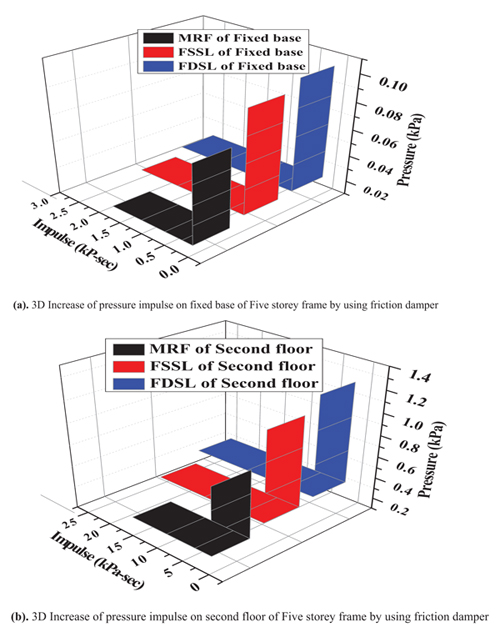
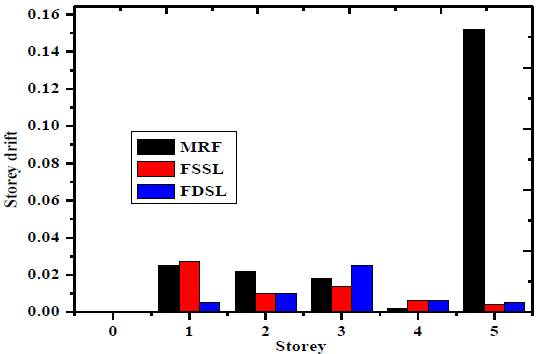
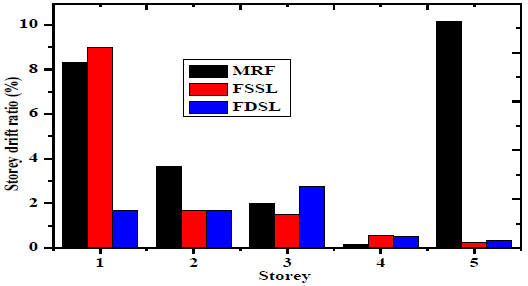
Fig. (12) shows the storey drift of the five-storey frame. The maximum storey drift occurs at fifth floor of 0.15 of MRF, 0.0095 and 0.0099 of FSSL and FDSL. The minimum storey drift occurs at fourth floor of 0.0095 of MRF, 0.0158 and 0.0195 of the FSSL and FDSL. Fig. (13) shows the storey drift ratio of the five-storey frame. The maximum storey drift ratio occurs at first floor of 8% of MRF, 9% of the FSSL and 1.8% of the FDSL. The minimum storey drift ratio occurs at fourth floor of 0.8% of MRF, 0.95% of the FSSL and 1% of the FDSL.

3.2. Eight Storey Frame

Fig. (14) represents three dimensions of the reduction of response of eight storey frame by friction damper. The maximum displacement occurs at fixed base of the MRF is 8m and is reduced to 6m and 5m of the FSSL and FDSL respectively. The maximum velocity occurs at fixed base of the MRF is 0.025m/sec and is reduced to 0.017m/sec and 0.015m/sec of the FSSL and FDSL respectively. The maximum acceleration occurs at fixed base of the MRF is 10m/sec2 and is reduced to 8m/sec2 and 7.5m/sec2 of the FSSL and FDSL respectively.

Fig. (12). Reduction of storey drift of Five storey frame by using friction damper.
Fig. (13). Reduction of storey drift ratio of Five storey frame by using friction damper.
Fig. (14). 3D Reduction of response on eight storey frames.

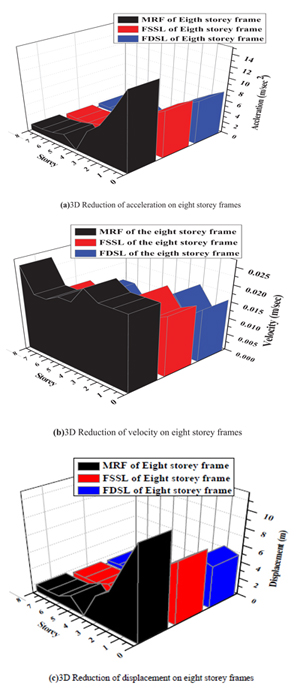
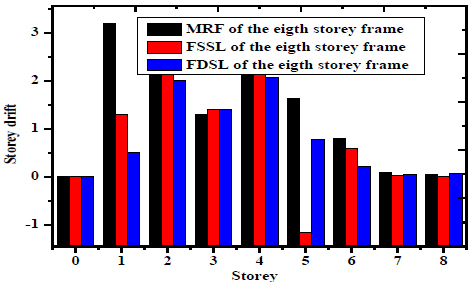
Figs. (15 and 16) shows the two- and three-dimensions reduction of the storey drift of the eight-storey frame. The maximum storey drift occurs at fourth floor of 2.1 of the MRF and is reduced to 2.05 and 2 of the FSSL and FDSL respectively. The minimum storey drift occurs at fixed base of 0.05 of the MRF and is reduced to 0.04 and 0.04 of the FSSL and FDSL respectively.

Fig. (15). 2D of reduction of storey drift of eight storey frame.
Fig. (16). 3D of reduction of storey drift ratio of eight storey frame.

3.3. Twenty Storey Frame

3.3.1. Along x Direction

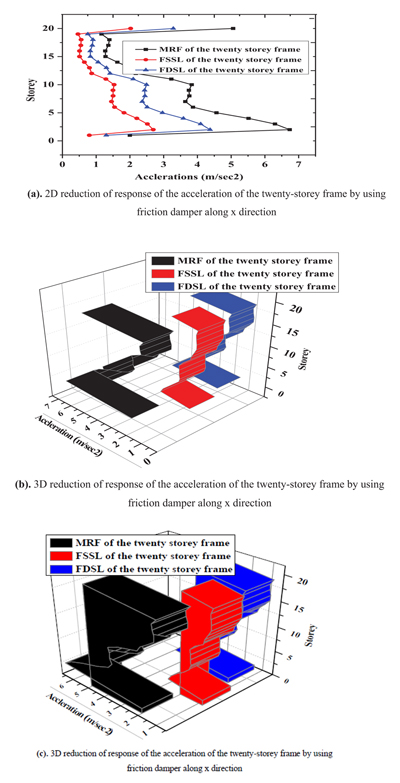
Fig. (17) represents reduction both 2D and 3D of the acceleration of the twenty-storey frame by using friction damper. The maximum acceleration occurs at third floor of 7m/sec2 of the MRF frame and the acceleration is reduced to 4.5m/sec2 and 2.8 m/sec2 of the FSSL and FDSL respectively.

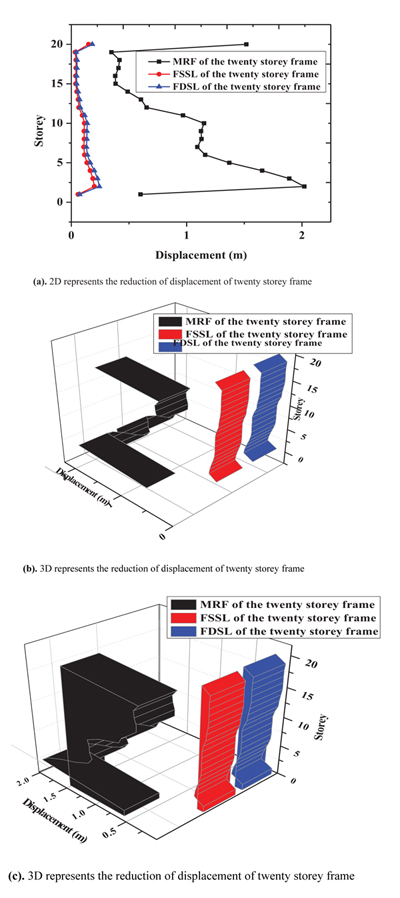
Fig. (18) represents the reductions of the displacement of the twenty-storey frame along x direction in 2D and 3D. The maximum displacement occurs at third floor of 2m of the MRF and is reduced to 0.25m and 0.2m of the FSSL and FSDL respectively.

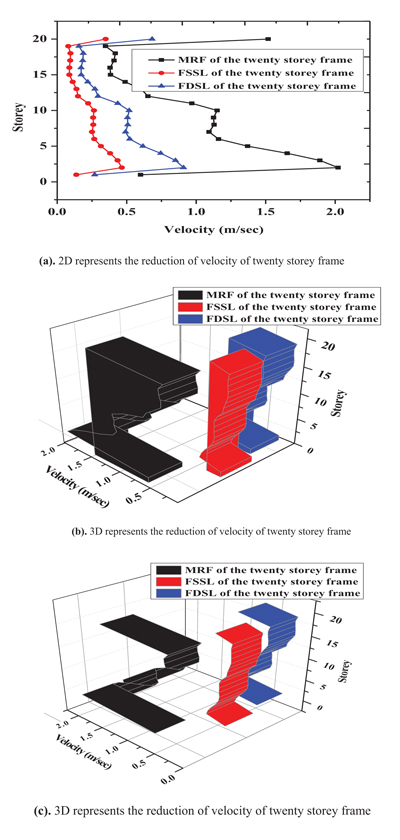
Fig. (19) represents the 2D and 3D of the reduction of the velocity of the twenty-storey frame along x direction by using friction damper. The maximum velocity occurs at third floor of 2m/sec of the MRF and is reduced to 0.8m/sec and 0.5m/sec of the FSSL and FSDL respectively.

Fig. (17). Reduction of the acceleration of the twenty-storey frame along x direction.
Fig. (18). Reduction of displacement of twenty storey frame.
Fig. (19). Reduction of velocity of twenty storey frame.

3.3.2. Along y Direction

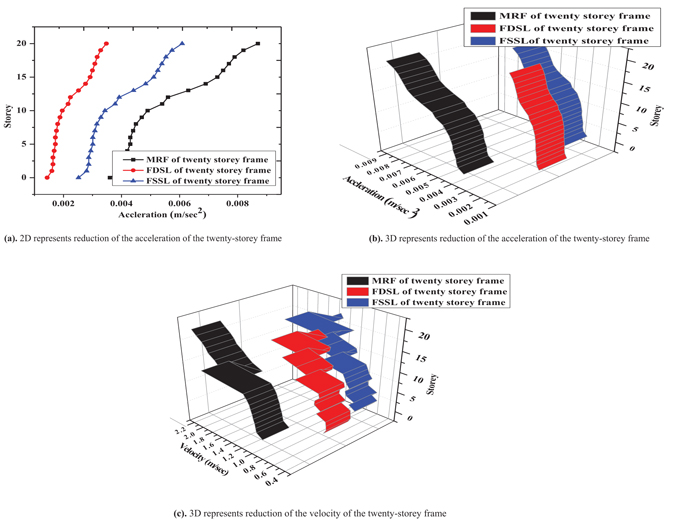
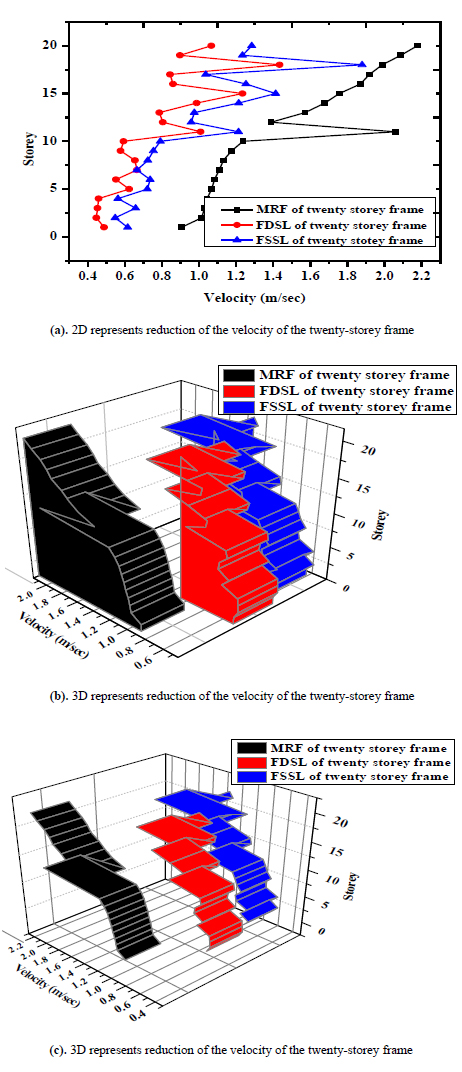
Fig. (20) shows two dimensional and three dimensional representing the reduction of the acceleration of the twenty-storey frame along y direction. The maximum acceleration occurs at twenty storeys of 0.009 m/sec2 of the MRF and is reduced to 0.006 m/sec2 and 0.003 m/sec2 of the FSSL and FSDL respectively. Fig. (21) shows two dimensional and three dimensional representing the reduction of the velocity of the twenty-storey frame along y direction. The maximum velocity occurs at twenty storeys of 2.2 m/sec of the MRF and is reduced to 1.3 m/sec and 1 m/sec of the FSSL and FSDL respectively.

Average performance and torsional moment of twenty storey frame are shown in Tables 8 and 9 respectively.

Fig. (20). Reduction of acceleration of twenty storey by using friction damper of twenty storey frame along y direction.
Fig. (21). Reduction of velocity by using friction damper of twenty storey frame along y direction.
Table 8.
Average performance of the FSSL and FSDL.
Sl No Response Parameter FSSL (Mode) FSDL (Mode)
I II III IV I II III IV
1 Drift ratio 0.8345 0.8210 0.7854 0.6845 0.7582 0.7412 0.7102 0.6845
2 Acceleration 0.642 0.689 0.624 0.598 0.645 0.660 0.610 0.690
3 Base shear 0.5480 0.5210 0.569 0.610 0.564 0.520 0.510 0.505
4 Average Drift 0.678 0.680 0.660 0.610 0.64 0.6215 0.6102 0.604
Table 9.
Torsional moment considered in twenty storey frames.
Sl No Floor Torsional moment along x direction Torsional moment along y direction
1 First 121 85
2 Second 120 88
3 Third 122 90
4 Fourth 121 95
5 Fifth 120 96
6 Sixth 112 98
7 Seventh 118 101
8 Eight 124 110
9 Ninth 126 120
10 Tenth 128 112
11 Eleventh 129 116
12 Twelve 134 112
13 Thirteen 138 114
14 Fourteen 142 116
15 Fifteen 145 124
16 Sixteen 149 108
17 Seventeen 180 104
18 Eighteen 190 105
19 Nineteen 195 109
20 Twenty 195 109

CONCLUSION

The low rise, mid-rise, and high rise MRF with blast load. The response was calculated by using adaptive-based pushover analyses. The three-mode shapes are considered in the analyses of the frame. The different response parameters are displacement, velocity, accelerations, pressure impulse curve, normalized pressure impulse curve, storey drift, storey drift ratio are studied. The response is controlled by using a single slip load friction damper (FSSL) and double friction slip damper (FSDL). The following conclusions are drawn:

(1) The blast load performance of the MRF models was improved significantly under both single slip load damper and double slip load damper.

(2) The 20% and 30% reductions of the accelerations in all the frames by using a single slip load damper and double slip load damper.

(3) The extreme floors reaction of the DSL prepared dampers is disseminated more consistently along the height of the building models.

(4) As per this limited study, the most advisable buildings to be equipped with the proposed DSL damper are the mid-rise building models.

(5) The interstorey driftsare reduced to 30%, 60% by using a single slip load damper and double slip load damper, respectively.

(6) The results of the pressure impulse curve of the MRF, FSSL & FSDL are obtained by energy-based pressure impulse curve method.

(7) Performance of the blast load with highrise structural frame is analyzed by considering the torsional effects and response in two dimensions effects parameter.

(8) The 28% and 35% increase of the pressure and 25% and 30% increase of the impulse will not cause failure to the structural frame by using FSSL and FSDL.

(9) Shear force will be maximum at first floor of the five storey frame exposed to blast load and minimum occurs at fifth floor

(10) The maximum torsional moment occurs at twenty floor of 195 kNm along x directions and minimum occurs at lower storey along y directions of first floor of 85 kN m.

(11) The maximum lateral force occurs at first mode in eight floor and minimum lateral force occurs at first floor in the mode I.

(12) The displacement will be maximum along x directions in the eight-storey frame.

CONSENT FOR PUBLICATION

Not applicable.

AVAILABILITY OF DATA AND MATERIALS

Some or all data, models, or code that support the findings of this study are available from the corresponding author [E.N.F] upon reasonable request.

FUNDING

None.

CONFLICT OF INTEREST

The authors declare no conflict of interest, financial or otherwise.

ACKNOWLEDGEMENTS

None.

REFERENCES

1 Karandeep Singh, and Paolo Gardoni&Flavio Stochino, "Probabilistic models for blast parameters and fragility estimates of steel columns subject to blast loads", Engin. Structures, vol. 222, p. 110944,2020.[CrossRef Link] 2 J-H. Choi, S-J. Choi, J-H.J. Kim, and K-N. Hong, "Evaluation of blast resistance and failure behavior of prestressed concrete under blast loading", Constr. Build. Mater, vol. 178, pp. 550-572.[CrossRef Link] 3 C. Zhang, G. Gholipour, and A.A. Mousavi, "Nonlinear dynamic behaviour of simply-supported RC beams subjected to combined impact-blast loading", Eng. Struc, vol. 181, pp. 124-42.[CrossRef Link] 4 H. Draganić, G. Gazić, and D. Varevac, "Experimental investigation of design and retrofit methods for blast load mitigation: A state-of-the-art review", Eng. Struct., vol. 190, pp. no189-no209.[CrossRef Link] 5 X. Yang, Y. Li, Y. Chen, Y. Li, L. Dai, R. Feng, and Y. Duh, "Case study on the catastrophic explosion of a chemical plant for production of m-phenylenediamine", J. Loss. Prevent. Proc, vol. 67, no. 104232, .[CrossRef Link] 6 Q. Fang, S. Yang, L. Chen, J. Liu, and Y. Zhang, "Analysis on the building damage, personnel casualties and blast energy of the“8-12”explosion in Tianjin port", China Civ. Eng, vol. 50, pp. 12-18. 7 J. Li, and H. Hao, "Numerical study of medium to large scale BLEVE for blast wave prediction", J. Loss. Prevent. Proc., vol. 65, .104107[CrossRef Link] 8 X. Liang, Z. Wang, and R. Wang, "Deformation model and performance optimization research of composite blast resistant wall subjected to blast loading", J. Loss. Prevent. Proc., vol. 49, pp. 326-341.[CrossRef Link] 9 H. Regan, T. Qiblawi, G. Balkiz, B. Wedeman, and L. McGee, Ammonium nitrate stored in a warehouse linked to catastrophic beirut explosion., CNN, . 10 Shao-bo Qi, Guang-yan Huang, Xu-dong Zhi, Feng Fan, and G.J. Richard, "External blast load factors for dome structures based on reliability", Def. Technol, .[CrossRef Link] 11 S. Qi, X. Zhi, F. Fan, and R.G.J. Flay, "Probabilistic blast load model for domes under external surface burst explosions", Struct. Saf., vol. 87, no. 102004, .[CrossRef Link] 12 Z-X. Li, X. Zhang, C. Wu, and J. Li, "Finite element Modeling of FRP retrofitted RC column against blast loading", Compos. Struct., vol. 263, no. 113727, .[CrossRef Link] 13 O.A. Ardila-Giraldo, and S. Pujol, "Initial shear demand in beams and one-way slabs subjected to blast load", Structures, vol. 32, pp. 1679-169.[CrossRef Link] 14 Sameer Khan, Sandip Kumar Saha, Vasant A. Matsagar, and Benno Hoffmeister, "Fragility of steel frame buildings under blast load", J. Perform. Construct. Facilities, p. 04017019.[CrossRef Link] 15 Mahmoud T. Nawar, T. Ibrahim, and Arafa & Osama M Elhosseiny, "Numerical damage evaluation of perforated steel columns subjected to blast loading", Def. Technol, .[CrossRef Link] 16 X. Zhang, Y. Ding, and Y. Shi, "Numerical simulation of far-field blast loads arising from large TNT equivalent explosives", J. Loss Prevent. Proc. Industr, vol. 70, no. 104432, .[CrossRef Link] 17 Tathagata Roy & Vasant Matsagar, "Probabilistic framework for failure investigation of reinforced concrete wall panel under dynamic blast loads", Engin. Fail. Analysis, vol. 125, p. 105368.[CrossRef Link] 18 K.K. Kiran, and E. Noroozinejad Farsangi, "Blast demand estimation of RC-moment-resisting frames using a proposed multi-modal adaptive pushover analysis procedure", Int. J. Engineer,Transact. B: Appl., vol. 34, no. 1, pp. 46-55.[CrossRef Link] 19 K. Ke, F. Wang, and C.H. Michael, "A multi-stage-based nonlinear static procedure for estimating seismic demands of steel MRFs equipped with steel slit walls", Eng. Struc, vol. 183, pp. 1091-1108.[CrossRef Link] 20 F. Gutiérrez-Urzúa, F. Freddi, and L. Di Sarno, "Comparative analysis of code-based approaches for seismic assessment of existing steel moment resisting frames", J. Construct. Steel Res., vol. 181, no. 106589, .[CrossRef Link] 21 L. Lombardi, F. De Luca, and J. Macdonald, "Design of buildings through linear time-history analysisoptimising ground motion selection: A case study for RC-MRFs", Eng. Struc., vol. 192, pp. 279-295.[CrossRef Link] 22 Rohan Bhasker & Arun Menon, "Torsional irregularity indices for the seismic demand assessment of RC moment resisting frame buildings", Structures, vol. 26, pp. 888-900.[CrossRef Link] 23 H. Arabzadeh, and K. Galal, "Seismic-response analysis of RC C-shaped core walls subjected to combined flexure, shear, and torsion", J. Struct. Eng., vol. 144, no. 10, .04018165[CrossRef Link] 24 Mohamed Draidi Bensalah, Mahmoud Bensaibi & Arezou Modaressid, "Uncertainties in seismic response of a torsional irregular structure", Eur. J. Environment. Civ. Engineer, pp. 1-11.[CrossRef Link] 25 C. Caruso, R. Bento, E.M. Marino, and J.M. Castro, "Relevance of torsional effects on the seismic assessment of an old RC frame wall building in Lisbon", J. Build. Eng., vol. 19, pp. 459-471.[CrossRef Link] 26 D. Farahani, F. Behnamfar, H. Sayyadpour, and M. Ghandil, "Seismic impact between adjacent torsionally coupled buildings", Soil. Dyn. Earthquake Eng., vol. 117, pp. 81-85.[CrossRef Link] 27 D. Farahani, F. Behnamfar, and H. Sayyadpour, "Effect of pounding on nonlinear seismic response of torsionally coupled steel structures resting on flexible soil", Eng. Struct., vol. 195, pp. 243-262.[CrossRef Link] 28 E. Abraik, "Numerical study for the impact of torsional amplification on the seismic response of self-centring braces equipped with different shape memory alloy materials", Structure, vol. 32, pp. 505-515.[CrossRef Link] 29 G. Ghayoumian, and A.R. Emami, "A multi-direction pushover procedure for seismic response assessment of low-to-medium-rise modern reinforced concrete buildings with special dual system having torsional irregularity", Structures, vol. 28, pp. 1077-1107.[CrossRef Link] 30 C.H.B.V. Hareen, and S.C. Mohan, "Evaluation of seismic torsional response of ductile RC buildings with soft first story", Structures, vol. 29, pp. 1640-1654.[CrossRef Link] 31 L. Zou, F. Li, J. Song, T. Shi, S. Liang, and O. Mercan, "Investigation of torsional aeroelastic effects on high-rise buildings using forced vibration wind tunnel tests", J. Wind Eng. Ind. Aerodyn., vol. 200, no. 104158, .[CrossRef Link] 32 R. Hoult, "Torsional capacity of reinforced concrete U-shaped walls", Structures, vol. 31, pp. 190-204.[CrossRef Link] 33 Y. Tsai, and T. Krauthammer, "Energy based load impulse diagram", Eng. Struct., vol. 149, pp. 64-77.[CrossRef Link] 34 Y. Yuan, L. Zhu, X. Bai, T.X. Yu, Y. Li, and P.J. Tan, "Pressure - impulse diagrams for elastoplastic beams subjected to pulse-pressure loading", Int. J. Solids Struct., vol. 160, pp. 148-157.[CrossRef Link] 35 J. Li, and H. Hao, "Numerical and analytical prediction of pressure and impulse from vented gas explosion in large cylindrical tanks", Process Saf. Environ. Prot., vol. 127, pp. 226-244.[CrossRef Link] 36 J. Li, F. Hernandez, H. Hao, Q. Fang, H.B. Xiang, Z. Li, X. Zhang, and L. Chen, "Vented methane-air explosion overpressure calculation: A simplified approach based on CFD", Process Saf. Environ. Prot., vol. 109, pp. 489-508.[CrossRef Link] 37 J. Li, H. Hao, Y.C. Shi, Q. Fang, Z. Li, and L. Chen, "Experimental and computational fluid dynamics study of separation gap effect on gas explosion mitigation for methane storage tanks", J. Loss Prev. Process Ind., vol. 55, pp. 359-380.[CrossRef Link] 38 J. Li, and H. Hao, "Far-field pressure prediction of a vented gas explosion from storage tanks by using new CFD simulation guidance", Process Saf. Environ. Prot., vol. 119, pp. 360-378.[CrossRef Link] 39 Chunwei Zhang, M. Abedini, and J Mehrmashhadi, "Development of pressure-impulse models and residual capacity assessment of RC columns using high fidelity arbitrary lagrangian-eulerian simulation", Engin. Structures, vol. 224, p. 111219.[CrossRef Link] 40 D. Zhao, and X. Wang, "New method to evaluate the rate of convergence for two-dimensional system involving friction damper", Structures, vol. 27, pp. 2513-2519.[CrossRef Link] 41 S. Etedali, K. Hasankhoie, and M.R. Sohrabi, "Optimal design of pure-friction isolators with and without restoring device: A multi-objective cuckoo search-based approach for seismic excited structures", Structures, vol. 25, pp. 708-719.[CrossRef Link] 42 H.C. Quintana, and M. Petkovski, "Optimum performance of structural control with friction dampers", Eng. Struct., vol. 172, pp. 154-162.[CrossRef Link] 43 E. Atam, "Friction damper-based passive vibration control assessment for seismically-excited buildings through comparison with active control: A case study", IEEE Access, vol. 7, pp. 4664-4675.[CrossRef Link] 44 Ghorbani, Hamid R.and Rofooei, Fayaz R., "A novel double slip loads friction damper to control the seismic response of structures", Eng. Struct., vol. 225, no. 111273, .[CrossRef Link] 45 F. Taiyaria, F.M. Mazzolanib, and S. Bagheri, "Damage-based optimal design of friction dampers in multistory chevron braced steel frames", Soil Dynam. Earthq. Engineer, vol. 119, pp. 11-20.[CrossRef Link] 46 N. Nabid, I. Hajirasouliha, and M. Petkovski, "Adaptive low computational cost optimisation method for performance based seismic design of friction dampers", Eng. Struct., vol. 198, no. 109549, .[CrossRef Link] 47 A. Naeem, and J. Kim, "Seismic retrofit of 3000 kVA power transformer using friction dampers and prestressed tendons", Structures, vol. 32, pp. 641-650.[CrossRef Link] 48 A. Zhang, Y. Zhang, A. Liu, D. Shao, and Q. Li, "Performance study of self-centering steel frame with intermediate columns containing friction dampers", Eng. Struct., vol. 186, pp. 382-398.[CrossRef Link] 49 A. Ghafouri-Nejad, A.B. Mehdi, S.M. Mirhosseini, and E. Zeighami, "Parametric study on seismic response of the knee braced frame with friction damper", Structures, vol. 32, pp. 2073-2087.[CrossRef Link] 50 A.S. Ana, F. Santos, and G. Rizzano, "Experimental response of friction dampers under different loading rates", Int. J. Impact Eng., vol. 132, no. 103316, . 51 A.F. Santos, A. Santiago, M. Latour, and G. Rizzano, "Analytical assessment of the friction dampers behaviour under different loading rates", J. Construct. Steel Res., vol. 158, pp. 443-459.[CrossRef Link] 52 B. Westenenk, J.J. Edwards, J.C. de la Llera, and R. Jünemann, "Self-Centering Frictional Damper (SCFD)", Eng. Struct., vol. 197, no. 109425, .[CrossRef Link] 53 S. Veismoradi, Seyed Mohamad Mahdi Yousef-beik, Yousef Beik, Pouyan Zarnani, and Pierre Quenneville, "Development and parametric study of a new self-cantering rotational friction damper", Eng. Struct., vol. 235, no. 112097, .[CrossRef Link] 54 S. Hu, W. Wang, B. Qu, and M. Shahria Alam, "Self-cantering energy-absorbing rocking core system with friction spring damper: Experiments, modelling and design", Eng. Struct., vol. 225, .111338[CrossRef Link] 55 V. Barzegar, S. Laflamme, A. Downey, M. Li, and C. Hu, "Numerical evaluation of a novel passive variable friction damper for vibration mitigation", Eng. Struct., vol. 220, .110920[CrossRef Link] 56 Z. Zhang, K. Bi, H. Hao, P. Sheng, L. Feng, and D. Xiao, "Development of a novel deformation-amplified shape memory alloy-friction damper for mitigating seismic responses of RC frame buildings", Eng. Struct., vol. 216, .110715[CrossRef Link] 57 Yongwei Wang, Bin Zeng, Zhen Zhou, and Qin Xie, "Hysteretic and seismic performance of dual self-centering variable friction damper braces", Soil. Dynam. Earthq. Engineer, vol. 147, p. 106774.[CrossRef Link] 58 A. Shirkhani, B.F. Azar, and M.C. Basim, "Seismic loss assessment of steel structures equipped with rotational friction dampers subjected to intensifying dynamic excitations", Eng. Struct., vol. 238, no. 112233, .[CrossRef Link] 59 H. Jarrahi, A. Asadi, M. Khatibinia, S. Etedali, and A. Samadi, "Simultaneous optimization of placement and parameters of rotational friction dampers for seismic-excited steel moment-resisting frames", Soil. Dynam. Earthq. Engineer, vol. 136, p. 106193.[CrossRef Link] 60 H. Jarrahi, A. Asadi, M. Khatibinia, and S. Etedali, "Optimal design of rotational friction dampers for improving seismic performance of inelastic structures", J. Build. Eng., vol. 27, .100960[CrossRef Link] 61 M.M. Javidan, and J. Kim, "Seismic retrofit of soft-first-story structures using rotational friction dampers", J. Struct. Eng., vol. 145, no. 12, .04019162[CrossRef Link] 62 W. Sui, X. Wang, and Z. Wang, "Experimental study on mechanical properties of the steel friction pads used in a rotational friction damper", Structures, vol. 29, pp. 1808-1818.[CrossRef Link] 63 T. Ying-kuan, and T. Krauthammer, "Energy based load-impulse diagrams with multiple failure modes for blast-loaded reinforced concrete structural elements", Eng. Fail. Anal., vol. 104, pp. 830-843.[CrossRef Link] 64 N. Nabid, I. Hajirasouliha, and M. Petkovski, "Simplified method for optimal design of friction damper slip loads by considering near-field and far-field ground motions", J. Earthq. Engineer, pp. 1-26.[CrossRef Link] 65 Georgi Bonchev, Borislav Belev & Imad Mualla, "Linked columns with friction dampers as a technique for seismic retrofit of steel moment resisting frames", ce/Papers, vol. 1, no. 2-3, pp. 3092-3099.[CrossRef Link]