RESEARCH ARTICLE
Assessment of Construction Project Cost Estimating Accuracy in Egypt
Ahmed H. Ibrahim1, Lamiaa M. Elshwadfy2, *
Article Information
Identifiers and Pagination:
Year: 2021Volume: 15
First Page: 290
Last Page: 298
Publisher ID: TOCIEJ-15-290
DOI: 10.2174/1874149502115010290
Article History:
Received Date: 12/2/2021Revision Received Date: 10/5/2021
Acceptance Date: 7/6/2021
Electronic publication date: 04/10/2021
Collection year: 2021
open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: https://creativecommons.org/licenses/by/4.0/legalcode. This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Background:
The accuracy of the cost estimate is a key success factor for any construction project. It is the base for an effective tendering process. It can also be considered as the cornerstone of the cost control process.
Objective:
This paper aims to develop a model that can be used to assess the expected cost estimating accuracy of construction projects. This model is named as Construction Cost Estimate Accuracy Index (CCEAI).
Methods:
A questionnaire survey that contains fifteen factors clustered into four categories was carried out among 90 experts based on the construction cost estimate. Only sixty-six questionnaires were returned. The Analytical Hierarchy Process (AHP) was used to identify the relative weights of the different cost estimates.
Results:
The questionnaire results were analyzed using the AHP technique to calculate the relative weight for each of the input factors and categories. A Construction Cost Estimating Accuracy Assessment model (CCEAI) was developed based on the calculated relative weights. Then, three projects were used as case study applications to check the validity of the proposed model. The results showed that the CCEAI model is greatly reliable in predicting the expected accuracy of the cost estimate.
Conclusion:
The results of this research and the developed model are very important and can be considered as a powerful tool to predict and improve the expected accuracy of any future construction cost estimate.
1. INTRODUCTION
The construction industry contributes significantly to global economic development [1] and the cost estimate is the most vital step involved [1, 2]. Construction cost estimation is the analysis and compilation of many items that contribute to and affect the project cost [2]. The cost estimate plays an important role in decision-making. Improving cost estimate accuracy will facilitate in effective time management and costs in construction projects [3].
Cost estimates are considered significant for economic development, therefore, they should be accurate and competitive [4]. Schottlandar stated that cost estimation could be used as a budgetary control tool [5]. Also, at the same time, it is considered a tool of management when starting any project. Accurate cost estimate generally results in the most economical project cost, while underestimating or overestimating often leads to greater actual expenditures [6].
An accurate construction cost estimate is very important to complete every construction project successfully. Moreover, it can be considered the key factor for the project's success at its early stage [7]. The cost estimate is prepared and used for different purposes, including feasibility studies, tendering phases, and construction phases [6, 8]. Predicting price and construction cost estimates are significant steps for project contractors, estimators, and owners [9]. This paper aims to develop a model to predict the expected accuracy of the construction cost estimate.
2. LITERATURE REVIEW
2.1. Factors Affecting the Accuracy of Construction Cost Estimate
Britto evaluated and ranked 59 factors that affect the cost estimate of road construction in Sri Lanka [10]. A questionnaire survey was used to rank these factors. The results indicated that the accuracy and reliability of cost information, materials’ price/availability/supply/quality/imports, clear and detailed drawings and specifications, and completeness of cost information are the most significant factors. Abdul Rahman et al. identified the main factors that caused cost overrun in Malaysia [11]. From the literature, 35 factors were identified and divided into 7 categories. The findings indicated that fluctuation in materials prices, cash flow and financial difficulties faced by contractors, and poor site management and supervision are the most significant factors.
Iyer and Jha used a questionnaire survey to identify the most important factors affecting cost performance in Indian construction projects [12]. The results revealed that the most important factors are conflict among project participants, ignorance and lack of nonexistence of cooperation, reluctance in a timely decision, and short bid preparation time. Alghonamy showed that five factors cause cost overrun in Saudi Arabia construction projects. These factors are bid awarded for lowest price, frequent changes in design, improve planning, long period between design and implementation, and payments delay [13].
Arif et al. identified those factors affecting the accuracy of the construction cost estimates in Pakistan [14]. From 46 project cost data, 60 factors were identified. These factors are divided into four dimensions. The involvement of the contractor in estimating procedures and labor rates is the most important factor. Shehu et al. studied the cost performance in Malaysian construction projects in terms of private and public sectors [15]. This study depended on the procurement method, tendering method, project size, and nature of projects. The results showed that the public sectors work better than the private sectors. Shabniya studied the factors affecting construction cost estimating accuracy in India [1]. From the available literature, 42 factors were identified. Based on some statistical analysis, these factors were evaluated and ranked. The most important factors were gross floor area, total duration, geographic conditions, changes in materials prices, market conditions, and level of design complexity.
Sayed et al. studied the factors affecting the cost estimate to improve the cost estimation in a construction project [16]. From the literature review, twenty-nine factors were collected and then reduced to nine factors by the Pareto technique. The nine factors were used to develop an arithmetical model. This model was tested by fourteen completed projects. The cost variances calculated by the model were 0.5% and 0.8% for each case. Bakr identified the most significant factors affecting the accuracy of cost estimates at the tendering phase in Jordan [17]. From the literature review, 59 factors were collected. A questionnaire survey was designed and distributed to 450 experts in construction. The RII was used to rank these factors. The results revealed that the level of experience of the estimation team, client's financial capabilities, and the experience of the project team are the most important factors. Akinradewo et al. studied the factors affecting the accuracy of road cost estimates in Ghana [18]. This research showed that improper project planning, insufficient preliminary site investigation, use of shortcuts, use of outdated market prices, and incorrect equipment productivity are the most important factors.
2.2. Cost Modeling
Many researchers have used different techniques to predict the accuracy of the construction cost estimate. Different techniques have been used to improve and predict the cost estimate, including Neural Network (NN) [19], regression analysis [20, 21], Case-Based Reasoning (CBR) [22], and Analytical Hierarchy Process (AHP).
Jumas et al. a Conceptual Cost Estimation (CCE) model was developed to improve the accuracy [23]. Multiple Regression Analysis (MRA) and Adaptive Neuro-Fuzzy Inference System (ANFIS) were used to develop the model. It was found that the developed model improves the Mean Absolute Percent Error (MAPE) by 2.8 percent. An et al. developed an AHP, CBR model to predict the cost of projects [24]. The developed model gave reliable and accurate costs. Norali and Osanloo developed a model for mining project cost estimating using Support Vector Regression (SVR) [25]. Economic and technical data from 52 projects were collected to establish the model. The model gave a reliable result for construction cost estimation. A prediction model has been developed with a MAPE of 1.4% for the unit cost of the highway project in Libya by changing Artificial Neural Networks (ANNS) structure, training functions, and training algorithms until an optimum model was developed [26].
Maruvachery et al. developed a model to predict the cost and time for large-scale underground cavern construction projects [27]. To test the validity of the model, data for one of the completed projects was used. The results revealed that the model provides well-estimated construction cost at a level of confidence of 95%. Then, two projects were used to check the validity of the predicted cost and time. The results showed that the proposed model is an effective tool to estimate construction cost and time.
Khodir and Elghandor examined the role of value management in controlling the cost overrun on residential projects in Egypt [28]. This study was performed by analyzing two cases of studies. A questionnaire survey was then performed to determine the impact of using VM in residential projects in Egypt. The results showed that by using VM methodology, 15-40% of the total cost of residential projects could be saved. El Sawalhi and Shehatto developed a model to predict the early construction cost [29]. The developed model gave more accurate results of about 94%.
Ji et al. developed a model to improve the accuracy of the cost estimate in Korea [30]. The CBR approach and the actual cost estimate for 164 building projects were used to develop the model Twenty projects were used to test the validity of the model. The results showed that the model is an effective tool to improve the accuracy of the project cost estimate. Parakevopoulou and Benardos analyzed and evaluated the tunnel construction costs in Greek [31]. CBR was used to develop a tool that is used as a database for similar projects. Nine tunnels were analyzed to develop the model. The results revealed that the model is effective in a similar approach in tunnel project construction costs.
Ahn et al. developed an accurate model to improve the accuracy of the cost estimate for construction projects [32]. The study used the CBR method to improve the construction cost estimate in the early stage. To evaluate the efficiency of the model, the Mean Absolute Error Rate (MAER), Mean Squared Deviation (MSD), Mean Absolute Deviation (MAD), and Standard Deviation (SD) were used. The results showed that CBR enhances the accuracy of the cost estimating process. Akinradewo et al. stated that to improve the road project's estimate in Ghana, the estimators should give more attention to factors, such as the clear definition of project scope, availability of sufficient design in format, formal feedback between design and estimating teams, and proper design documentation and information management [33]. A prediction model using an Artificial Neural Network (ANN) was developed. The prediction model consists of the most impactful causes of delays and costs overruns during the construction of Palm Oil Refinery projects which were ranked based on importance, severity and frequency. A series of 39 questions were developed from the questionnaire survey causing delays and cost overruns during the construction of palm oil refinery projects. Artificial Bee Colony (ABC) algorithm was used to develop the prediction model for palm oil construction projects [34].
3. THE RESEARCH OBJECTIVES
(1) To identify the most significant factors affecting the accuracy of cost estimates.
(2) To determine the relative weights for each factor by using the AHP (Analytical Hierarchy Process)
(3) Based on the relative weights developing a proposed model to predict the expected cost estimating accuracy (Construction Cost Estimating Accuracy Index (CCEAI)).
(4) To test the validity of the index.
4. RESEARCH METHODOLOGY
This research was performed through a three-stage methodology. Firstly, a questionnaire survey including seventy of the cost estimating accuracy factors was designed and distributed among construction contractors to identify the most important factors that significantly influence the cost estimate accuracy. The results of this step showed that there were only 15 factors that have a significant effect on the cost estimate accuracy. These factors are shown in Table 1. A careful inspection of this table clearly shows that these factors were clustered under four main categories.
Secondly, the Analytic Hierarchy Process (AHP) technique was used to identify the relative weights of the four main categories as well as the different factors within each category. Based on the relative weights, the proposed model was developed. Finally, three completed case study projects were used to test the validity of the proposed model.
4.1. Analytical Hierarchy Process
The Analytical Hierarchy Process (AHP) has been developed by Thomas Saaty [35, 36]. It is a multi-criteria decision-making approach that allows for a relative evaluation and optimization of alternatives. The AHP is focused on the use of pairwise comparisons that also lead to the development of a ratio scale. The AHP uses the process of the decision-making problem as a hierarchy, consisting of an overall objective, a group of alternatives, and a set of criteria linking the alternatives to the objective. The basis of the Analytical Hierarchy Process (AHP) is a group of axioms that carefully describe the scope of the problem area [37]. It is dependent on the well-defined mathematical structure of consistent matrices and their associated right proprietary ability to produce true or approximate weights [36, 38].
| Category | Factors | |
|---|---|---|
| Consultants, design parameters, information | F1 | Clear and detailed drawings, specifications, and project documentation |
| F2 | Experience and skill level of the estimator | |
| F3 | Completeness of cost information, quality, cost data, and details | |
| F4 | Quality of assumptions used in preparing the estimate | |
| Project characteristics | F5 | Accuracy of BOQ |
| F6 | Project complexity of design and construction | |
| F7 | Project duration | |
| F8 | Construction method/techniques/technology | |
| Contractor characteristics | F9 | Experience on similar projects |
| F10 | Management team (suitability, experience, performance) | |
| F11 | Financial capability | |
| F12 | Construction team's ability to control the project | |
| External factors | F13 | Materials (prices, availability, quality, imports) |
| F14 | Percentage of loss in construction materials | |
| F15 | Economic situation | |
Saaty [36], cited in Vaidya and Kumar [39], the Analytical Hierarchy technique is a multi-criteria decision-making tool. This is an important approach for pairwise comparisons. It also offers a technique for the calibration of the numerical scale to calculate both quantitative and qualitative results. The scale ranges from 1/9 (minimum valued than), to 1 (equal), and to 9 (absolutely more significant than), covering the entire spectrum of the comparison, as shown in Table 2. Some main and basic steps involved in this approach are as follows:
(1) Stating the issue.
(2) Extending the goals of the problem or to include all the participants, goals, and outcomes of the problem.
(3) Defining the criteria that affect the behavior of an individual.
(4) Stating the structure of the problem in a hierarchy of varying levels of purpose, criteria, sub-criteria, and alternatives.
(5) Comparing and calibrating each variable in the corresponding level on a numerical scale. This includes n(n-1)/2 comparisons, where n is the number of elements with the considerations that the diagonal elements are equal or (1) and the other elements are simply the reciprocals of the earlier comparisons.
(6) Conducting calculations to find the Highest Eigen Value, Consistency Index CI, Consistency Ratio CR, and Normalized Values for each criterion/alternative according to Eqs. (1 and 2).
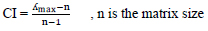
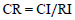
(7) If the maximum own value, CI, and CR are acceptable, then a decision shall be made based on the normalized values; otherwise, the process shall be repeated until those values are within the target range.
AHP questionnaire was designed and then distributed among 90 experts in the construction cost estimating field. Sixty-six questionnaires were returned, representing 73.33%. Table 3 shows the classification of the respondents according to their experience.
5. RESULTS AND DISCUSSION
5.1. AHP Results
A questionnaire was analyzed, and the relative weight for each of the main four categories and the input factors within each category were calculated. A summary of the calculated priorities weights is shown in Table 4.
Table 4 summarizes all priority weights for each category and its sub-elements. The contractor characteristics’ category is the most effective category in Construction Cost Estimate (CCE) with a relative weight of 0.31. In addition, factor economic situation is the most significant factor affecting (CCE) with a relative weight of 0.38.
| Intensity of Importance | Definition | Explanation |
|---|---|---|
| 1 | Equal importance | Two activities contribute equally to the objective. |
| 3 | Moderate importance | Experience and judgment slightly favor one activity over another. |
| 5 | Strong importance | Experience and judgment strongly favor one activity over another. |
| 7 | Very strong or demonstrated importance | An activity is favored very strongly over another; its dominance is demonstrated in practice. |
| 9 | Extreme importance | The evidence favoring one activity over another is of the highest possible order of affirmation. |
| 2, 4, 6, 8 | Intermediate values | When compromise is needed |
| Years of Respondents in Construction Projects | Project Manager | Cost Estimator | Site Engineer | Total |
Percent % |
|---|---|---|---|---|---|
| (Less than 10 years) | - | 6 | 7 | 13 | 19.7% |
| (Greater than or equals to 10 and less than 20) | 4 | 8 | 8 | 20 | 30.3 % |
| (Greater than or equals to 20 years) | 13 | 20 | - | 33 | 50% |
| Total | 17 | 34 | 15 | 66 | 100 |
| Category | Factor Weight | Overall Weight |
|---|---|---|
| C1 (Consultants, design parameters, information) | 0.26 | - |
| C2 (Project characteristics) | 0.22 | - |
| C3 (Contractor characteristics) | 0.31 | - |
| C4 (External factors) | 0.20 | - |
| Consultants, design parameters, information, and estimators | Factor weight | - |
| F1 (Clear and detailed drawings, specifications, and project documentation) | 0.27 | 0.07 |
| F2 (Experience and skill level of the estimator) | 0.26 | 0.07 |
| F3 (Completeness of cost information, quality, cost data, and details) | 0.27 | 0.07 |
| F4 (Quality of assumptions used in preparing the estimate) | 0.21 | 0.055 |
| Project characteristics | Factor weight | - |
| F5 (Accuracy of BOQ) | 0.24 | 0.053 |
| F6 (Project complexity of design and construction) | 0.28 | 0.062 |
| F7 (Project duration) | 0.25 | 0.055 |
| F8 (Construction method/techniques/technology) | 0.23 | 0.051 |
| Contractor characteristics | Factor weight | - |
| F9 (Experience on similar projects) | 0.26 | 0.081 |
| F10 (Management team (suitability, experience, performance)) | 0.24 | 0.074 |
| F11 (Financial capability) | 0.29 | 0.09 |
| F12 (Construction team's ability to control the project) | 0.21 | 0.065 |
| External factors | Factor weight | - |
| F13 (Materials’ prices, availability, quality, imports) | 0.35 | 0.07 |
| F14 (Percentage of loss in construction materials) | 0.27 | 0.054 |
| F15 (Economic situation) | 0.38 | 0.076 |
5.2. Model Development
After the weight of each factor and category was calculated, the construction cost estimate accuracy index (CCEAI) was developed from Eq. (3).
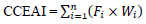
Where:
CCEAI: Construction Cost Estimating Accuracy Index,
F: factor affecting construction cost estimate
W: the weight of construction of the specified cost estimate accuracy factors,
n: number of construction cost estimate factors.
Using factor weights developed from AHP, the Construction Cost Estimating Accuracy Index model is presented below:
CCEAI = 0.27*[(0.26*F1) + (0.26*F2) + (0.27*F3) + (0.21*F4)] + 0.22*[(0.24*F5) + (0.28*F6) + (0.25*F7) + (0.23*F8)] + 0.31*[(0.26*F9) + (0.24*F10) + (0.29*F11) + (0.21* F12)] + 0.2*[0.35*F13) + (0.27*F14) + (0.38*F15)
5.3. Cost Performance Scale
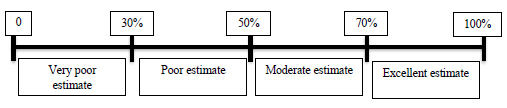
To quantify the calculated cost performance index, a questionnaire survey was designed and sent to a panel consisting of 8 experts (three project managers, three cost estimators, and two site engineers). According to the experts' opinion, a cost-performance scale was developed to interpret the score calculated by the proposed accuracy model. Such scale ranged between 0 and 100. According to the expert's opinions, a score range of 0-30 represents a very poor estimate, (30-50) represents a poor estimate, 50-70 represents a moderately accurate estimate, and 70-100 represents an excellent estimate, as shown in Fig. (1).
 |
Fig. (1). Cost performance scale. |
5.4. The Validity of the Model
5.4.1. Factors Relevant Score
For consistency and easy use of the proposed model, some guidelines on how to assess and quantify the input factors are provided in Table 5.
A careful inspection of Table 5 reveals that all factors will have a score ranging between (0-100). For example, clear and detailed drawings, specifications, and project documentation scores range from 0-100. The user should assign a score of 25 points to each factor in Table 5 and finally aggregate these limitation scores. Another example, the score of “accuracy of BOQ” ranges between 0-100. The user should select the score corresponding to the percentage of variation between BOQ and shop drawing shown in the factor limitation. Let us assume that the variation between BOQ and shop drawings ranges between 60%-80% and the corresponding factor score is 40%.
| Score | Factor Limitation | Measure Unit | Factor | Code | Category | |
|---|---|---|---|---|---|---|
| From 25 | - | Complete drawings and clear specifications | Clear and detailed drawings, specifications, and project documentation | F1 | Consultants, design parameters, information | |
| - | Complete drawings | |||||
| - | Complete specifications | |||||
| - | Clear specifications | |||||
| - | Match the specifications to the drawings | |||||
| - | Total | |||||
| - | Upper limit | Lower limit | Experience years of the estimator | Experience and skill level of the estimator | F2 | |
| ≤20% | ≤2 | 0 | ||||
| 40% | ≤4 | 2 | ||||
| 60% | ≤6 | 4 | ||||
| 80% | ≤8 | 6 | ||||
| 100% | ≥10 | |||||
| Score from 20 | - | Cost data completed, updated, according to similar projects and their sources | Completeness of cost information, quality, and details | F3 | ||
| - | Reliable source | |||||
| - | Updated | |||||
| - | From different projects | |||||
| - | Completed cost information | |||||
| - | according to similar projects | |||||
| - | Total | |||||
| Score | - | Level of details | Quality of assumptions used in preparing the estimate | F4 | ||
| 50% | Work items | |||||
| 75% | Subitems | |||||
| 100% | Cost elements | |||||
| 20% | Variation ≥80% | The variation between quantity surveyor from drawings and BOQ | Accuracy of BOQ | F5 | Project characteristics | |
| 40% | 60%<Variation ≤80% | |||||
| 60% | 40%<Variation ≤60% | |||||
| 80% | 20%<Variation ≤40% | |||||
| 100% | Variation ≤20% | |||||
| 20% | Tunnels undersea and bridges overseas | According to project type | Project complexity of design and construction | F6 | ||
| 40% | Road tunnels and bridges | |||||
| 60% | Mall and huge government buildings | |||||
| 80% | Roads | |||||
| 100% | Residential and administrative buildings | |||||
| 20% | Duration≥5 | - | Project duration | F7 | ||
| 40% | 5years>Duration=4 | |||||
| 60% | 4 years> Duration=3 | |||||
| 80% | 3 years> Duration=2 | |||||
| 100% | 2 years> Duration≥1 | |||||
| 20% | ≤two times | Number of times the construction method used | Construction method/ techniques /technology | F8 | ||
| 40% | 2< no of used ≤3 | |||||
| 60% | 3< no of used ≤4 | |||||
| 80% | 4< no of used =5 | |||||
| 100% | no of used >5 | |||||
| 20 | 1 projects | No of projects | Experience on similar projects | F9 | Contractor characteristics | |
| 40 | 2 projects | |||||
| 60 | 3 projects | |||||
| 80 | 4 projects | |||||
| 100 | ≥5 projects | |||||
| 20% | 0<ex. Year≤1 | According to the management team (cost Control) experience years | Management team(suitability, experience, performance) | F10 | ||
| 40% | 1<ex. Year≤3 | |||||
| 60% | 3<ex. Year≤5 | |||||
| 80% | 5<ex. Year≤7 | |||||
| 100% | Ex. Year≥ 7 | |||||
| 20% | 1≤C.R<1.5 | According to current ratio = ( current assets/short term liabilities) | Financial capability | F11 | ||
| 40% | 1.5≤C.R<2 | |||||
| 60% | 2≤C.R<2.5 | |||||
| 80% | 2.5≤C.R<3 | |||||
| 100% | C.R ≥3 | |||||
| 20% | 0<ex. Year≤1 | Experience years | Construction team's ability to control the project | F12 | ||
| 40% | 1<ex. Year≤3 | |||||
| 60% | 3<ex. Year≤5 | |||||
| 80% | 5<ex. Year≤7 | |||||
| 100% | >7 | |||||
| - | Upper limit | Lower limit | According to rising in prices | Materials (prices, availability, quality, imports) | F13 | External factors |
| 20% | ≤25 | 20˂ | ||||
| 40% | ≤20 | 15˂ | ||||
| 60% | ≤15 | 10˂ | ||||
| 80% | ≤10 | 5˂ | ||||
| 100% | ≤5 | 0˂ | ||||
| - | Upper limit | Lower limit | According to the percentage of loss | Percentage of loss in construction materials | F14 | |
| 20% | ≥5 | |||||
| 40% | 4 | 3 | ||||
| 60% | 3 | 2 | ||||
| 80% | 2 | 1 | ||||
| 100% | ≤1 | |||||
| - | Upper limit | Lower limit | According to the inflation rate | Economic situation | F15 | |
| 20% | ≥25 | 20 | ||||
| 40% | 20 | 15 | ||||
| 60% | 15 | 10 | ||||
| 80% | 10 | 5 | ||||
| 100% | 5 | - | ||||
5.4.2. Case Studies
Three case studies were applied to check the validity of the proposed model. The cost estimating accuracy score was calculated using Eq. (3). The results of those case studies were compared with the actual cost accuracy. The actual cost accuracy was calculated based on the comparison between the actual and estimated cost of those projects, according to Eq. (4).
5.4.2.1. First Case Study
“Beni-Suef power planet 4×1200 MW” is the first case study. The estimated cost for this project was, for example, 176,986,366, and the actual cost was, for example, 196,378,317. Several steps should be followed to complete the evaluation as follows:
(1) Project data to be assessed for each input factor.
(2) Table 5 to be used to obtain the input factor score.
(3) Use Eq. (3) to calculate CCEAI, which resulted in 83.37.
(4) The actual Accuracy to be calculated according to Eq. (4):
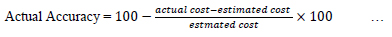
The value indicates the project cost estimate as an excellent estimate. By comparing calculated accuracy (83.37%) with actual accuracy, (89%), it can be indicated that the project is an “excellent estimate”.
5.4.2.2. Second Case Study
“Water treatment plant” is the second case study. The estimated cost for this project was, for example, (168,000,000) and the actual cost was, for example, (188,000,000). Several steps should be followed to complete the evaluation as below:
(1) Project data to be assessed for each input factor.
(2) Table 5 to be used to obtain the input factor score.
(3) Eq. (3) to be used to calculate CCEAI, which resulted in 81.44.
By comparing the calculated accuracy (81.44%) with the actual accuracy (88%) from Eq. (4), it can be indicated that the project is an “excellent estimate”.
5.4.2.3. Third Case Study
“Five residential buildings consisting of a basement floor, ground floor, and two stories” were used as the third case study. The estimated cost for this project was, for example, 31,700,000, and the actual cost was, for example, 50,475,000. Several steps should be followed to complete the evaluation as below:
(1) The project data to be assessed for each input factor.
(2) Table 5 to be used to obtain the input factor score.
(3) Eq. (3) to be used to calculate CCEAI, which resulted in 58%.
The value indicates the project cost estimate as a moderate estimate. By comparing 58% calculated accuracy with 59.23% actual accuracy calculated from Eq. (4), it can be indicated that the project is a “moderate estimate.”
Hint: This paper is extracted from the master thesis conducted by Lamiaa M. Elswadfy .the supervised by Ahmed H. Ibrahim [40].
CONCLUSION
Through this paper, the most significant factors, i.e., 15, affecting the construction cost estimate accuracy were identified.. These factors are clear and detailed drawings, specifications, and project documentation, experience and skill level of the estimator, completeness of cost information, quality, cost data, and other cost-related details, quality of assumptions used in preparing the estimate, accuracy of BOQ, project complexity of design and construction, project duration, construction method/techniques/technology, experience on similar projects, the management team’s suitability, expe- rience, performance, financial capability, construction team's ability to control the project, and materials (prices, availability, quality, imports), percentage of loss in construction materials, and economic situation.
Then the Analytical Hierarchy Process (AHP) was used to develop a model to predict the accuracy of the cost estimate for any construction project. A questionnaire survey was carried out among 90 experts. Sixty-six questionnaires were returned. These questionnaires were analyzed, and the relative weights for the most important cost estimating accuracy factors were identified. The CCEAI model was then developed, as shown below:
CCEAI = 0.27*[(0.26*F1) + (0.26*F2) + (0.27*F3) + (0.21*F4)] + 0.22*[(0.24*F5) + (0.28*F6) + (0.25*F7) + (0.23*F8)] + 0.31*[(0.26*F9) + (0.24*F10) + (0.29*F11) + (0.21* F12)] + 0.2*[0.35*F13) + (0.27*F14) + (0.38*F15)
In addition, the validity of the model was tested by using three case studies applications. The validation process results provided a good indicator regarding the ability to use the proposed model to assess the accuracy of the construction project cost estimate.
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
The data used to support the findings of this study are included in the article.
FUNDING
None.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.
