RESEARCH ARTICLE
Behavior of Fibrous Reinforced Concrete Splices
Mereen H.F. Rasheed1, Ayad Z.S. Agha1, *, Bahman O. Taha1
Article Information
Identifiers and Pagination:
Year: 2021Volume: 15
First Page: 441
Last Page: 462
Publisher ID: TOCIEJ-15-441
DOI: 10.2174/1874149502115010441
Article History:
Received Date: 30/12/2020Revision Received Date: 23/8/2021
Acceptance Date: 7/9/2021
Electronic publication date: 31/12/2021
Collection year: 2021
open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: https://creativecommons.org/licenses/by/4.0/legalcode. This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Background:
The tangent of the relationship between bond stress and displacement (slip) is called the modulus of displacement and gives the basis for the theory. This theory is used to determine the stress distribution along the spliced reinforcement bars.
Objective:
This research presents a modification on the theory of the modulus of displacement to determine the stress distribution along the spliced reinforcement bond for fibrous reinforced concrete.
Methods:
1- General differential equations are derived for concrete stress, stress in reinforcement bars and bond stress between reinforcement bars and surrounding concrete.
2-The general solutions of these D.E. are determined and Excel data sheets are prepared to apply these solutions and determine the concrete, steel and bond stresses.
Results:
Excel data sheets are prepared to determine the concrete, steel and bond stresses. The stresses are determined along the bar splice length considering the effect of steel fiber content.
Conclusion:
The maximum concrete stress is obtained at center x=0 and minimum at
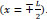. Maximum bond stress obtained at
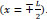and minimum at the center. The maximum steel stress at
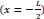and minimum at
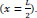. The value of (σcmax) increased linearly with increasing of (ρ). The concrete stress increased nonlinearly with (ρ%) and linearly with ( fy) and (fc’). Also increasing of (k) and bar diameter have small effects. The value of bond stress decreased linearly with (Qf) and (ρ%).
