GEO5 Slope Stability Analysis [27] commercial program based on Mohr-Coulomb soil strength criterion is used to determine the transmission tower slope-pile stability, critical slip surface location and the active and passive forces acting on the stabilizing pile wall. Then these computed active and passive forces and slip surface location are transferred to GEO5 AntiSlide Pile commercial program [28] based on pile foundation on Winkler soil model to compute the distributions of the internal forces, bending moment and displacement of the stabilizing piles.

Moamen [29] employed the similar GEO5 software to investigate the performance of 200 reinforced concrete piles with 0.6 m diameter, 10 m long and 2.4 m spacing used to stabilize an 8-m high railway embankment of Weald Clay at Hildenborough, Kent, UK. The computed results show that using the anti-slide piles is an effective method to increase the factor of safety for the slopes.

The validation of the present method was performed by comparing the results with those obtained from other methods.

Hassiotis et al. [18] and Won et al. [19] carried out numerical analyses to study the effect of stabilizing piles on the stability of an idealized slope by using a pressure-based coupled analysis and Bishop’s simplified analysis, respectively. The idealized homogeneous slope has a height of 13.7m with a slope angle of 30˚, unit weight of 19.63 kN/m³, cohesion of 23.94 kN/m² and friction angle of 10˚. A row of concrete piles with a diameter (d) of 0.62m embedded into a stable layer was used.

Fig. (1) shows that the rate of increase in the safety factor of a slope decreases with increasing the pile spacing (s) computed by the three methods. It also shows that the safety factor computed by present analysis is similar to that by the simplified Bishop analysis (Won et al. [19]) but slightly higher than that by the pressure-based coupled analysis (Hassiotis et al. [18]).

Fig. (1). Effect of pile spacing on factor of safety (Lx/x=0.5).

Fig. (2). Effect of pile location on factor of safety (s/d=2.5).

Fig. (3). Schematic diagram for stability analysis of transmission tower slope reinforced with multi-row piles in layered soil.

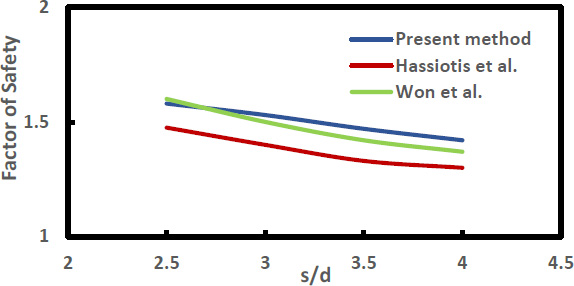
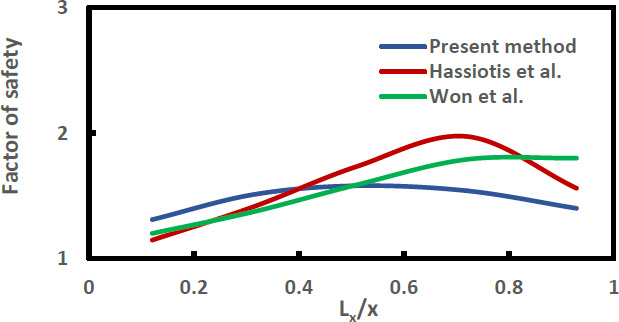
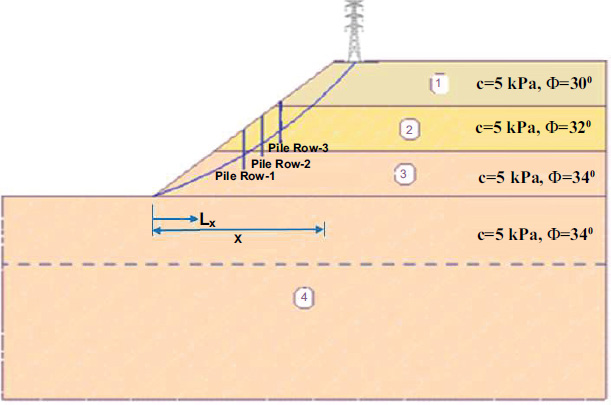
Fig. (2) shows the effect of the pile positions on the safety factor of a slope stabilized with piles (where L_x= pile location from slope toe and x= slope width). The numerical results computed by the present method indicate that the safety factor is largest when the piles are placed near to the middle of the slopes. However, the solutions obtained by using the pressure-based coupled analysis (Hassiotis et al. [18]) and Bishop simplified analysis (Won et al. [19]) indicate that the piles should be placed slightly towards to the crest of the slope for the largest safety factor.

A numerical assessment of the performance of small diameter steel pile as a stabilizing element for transmission tower slope stability was performed using the present uncoupled method. The small diameter steel piles used are steel pipe piles with 90 mm in diameter, 5 mm in thickness, 6 m in length and has a Young’s modulus of 2x10¹¹ kN/m². The properties of the homogeneous weathered residual soil slope are: cohesion (c) = 5 kN/m², friction angle (φ) = 35˚, unit weight= 18 kN/m³, slope height= 20 m and slope inclination (β) = 40°. Fig. (3) shows the soil properties used in layered weathered residual soil slope. The water table was not considered here. A 137kV transmission tower with 996 kN axial load was assumed located on the slope crest. The parametric study carried out was based on these soil and pile properties unless otherwise stated.

To assess the effect of small diameter passive piles on the stability conditions of a transmission tower slope, a conceptual slope profile with multi-row piles in parallel arrangement was used as shown in Fig. (3) (where L_x= pile location from slope toe and x= slope width). To focus on the comparison in terms of pile row effect, normalised pile spacing of s/d=3 (where s= pile spacing and d=pile diameter), normalised pile row spacing of s_r/x=0.1 (where s_r= pile row spacing and x=slope width) for multi-row small diameter steel piles were employed in the parametric study.

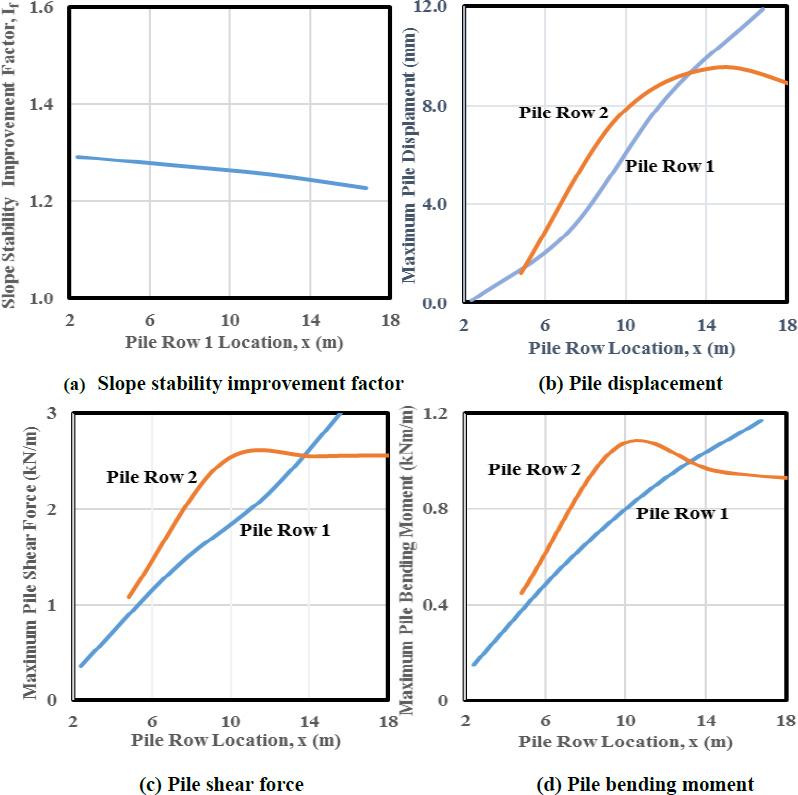
Fig. (4) shows the slope stability improvement factor I_f=F_p/F_s (F_s= factor of safety for unreinforced tower slope and F_p= factor of safety for pile reinforced tower slope) of the transmission tower slope for two-row small diameter steel piles decreases with an increase of pile location (L_x) from the slope toe indicating the piles more effectively reinforce the slope where the stabilizing force can produce maximum stabilzation effect when they are closer to the slope toe. Fig. (4b-4d) show the corresponding maximum pile displacement, shear force and bending moment increase with increasing pile location (L_x). However, for the Pile Row-2, they increase up to the middle of the slope and then decrease thereafter. It is observed that the Pile Row-2 are subjected to more soil pressure resulting higher maximum pile displacement, shear force and bending moment than the Pile Row-1 due to soil arching mechanism.

Fig. (4a-d). Variation of slope stability improvement factor (If), maximum pile diaplacement, shear force and bending moment with pile row location for two-row piles.

Fig. (5a-d). Variation of slope stability improvement factor (If), maximum pile diaplacement, shear force and bending moment with soil cohesion (c) for two-row piles.

Fig. (6a-d). Variation of slope stability improvement factor (If), maximum pile diaplacement, shear force and bending moment with soil friction angle (Ф) for two-row piles.

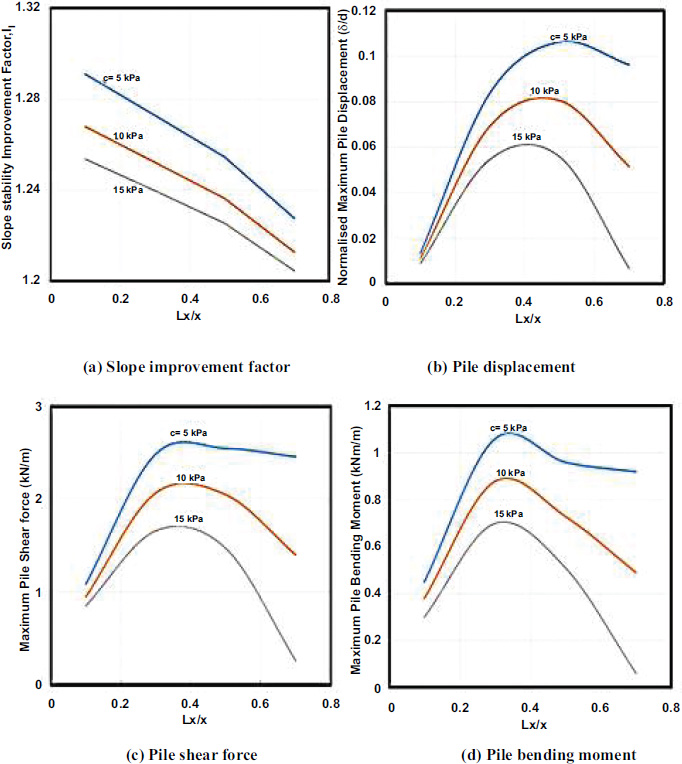
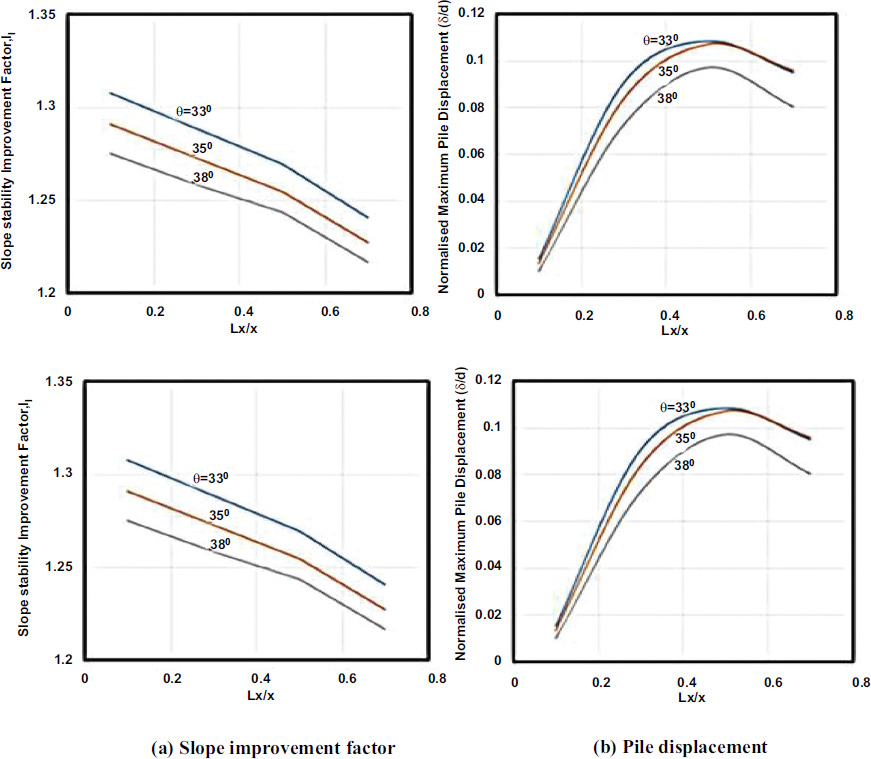
The factor of safey (F_p) for a slope reinforced with two-row small diameter steel piles increases with increasing soil strength parameters (c and ϕ). The rate of increase in F_s appears to be higher than that in F_p resulting smaller slope improvement factor (I_f=F_p/F_s) with increasing soil strengths parameters as shown in Figs. (5 and 6). The maximum pile displacement, shear force and bending moment decrease with increasing soil strength parameters. However, they increase up to the middle of the slope and then decrease thereafter. The increasing soil strength parameters may change the main mode of the pile movement from translation to rotation.

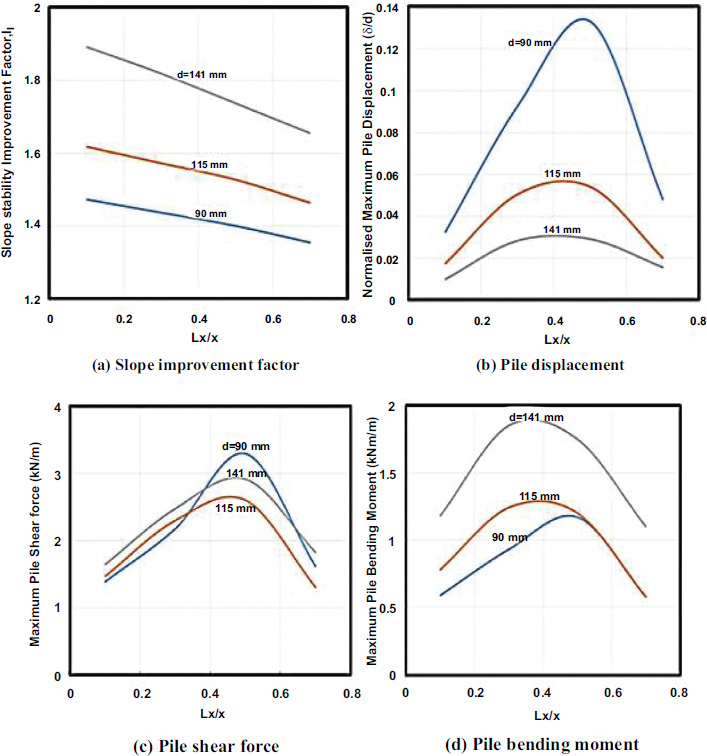
Fig. (7) shows the slope improvement factor (I_f) for three-row piles increases with increasing pile diameter (d) with constant pile length (L). The maximum pile displacement decreases with increasing pile diameter due to increase in structural stiffness. It appears that larger diameter pile develops minimum displacement but greater bending moment value. Whereas smaller diameter pile develops maximum displacement but lower bending moment value. The stiffer piles provide larger resistance to movement, and as a result, are more effective in mitigating a failing slope. However, the larger diameter piles are also heavier, harder to drive and more expensive.

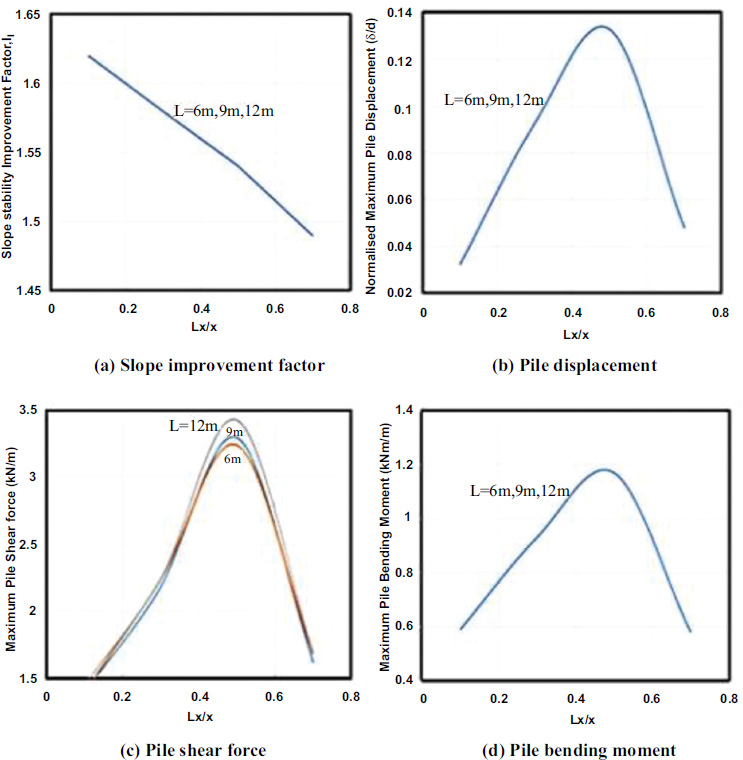
The failure mechanism depends on the embedded pile length within the underlying stable soil layer in the slope. The small diameter steel pile length used in this study which is greater than its critical length has little effect on the slope improvement factor (I_f), maximum pile displacement, shear force and bending moment as shown in Fig. (8). The maximum pile displacement, shear force and bending moment increase with increasing pile location (L_x) from the slope toe. However, they increase up to the middle of the slope and then decrease thereafter.

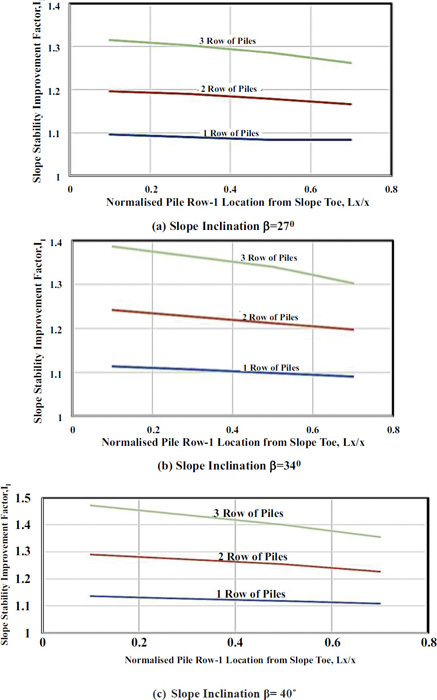
Fig. (9) shows that the slope improvement factor (I_f) increases with increasing number of pile rows for various slope inclinations. The multi-row small diameter steel piles have been found to be more resistance to soil movement due to multiple soil arching effects that can provide greater resisting force resulting higher factor of safety of the transmission tower slope. The multi-row small diameter steel piles may be more effective and economical than the single-row small diameter steel piles under large landslide thrust force.

Fig. (7a-d). Variation of slope stability improvement factor (If), maximum pile diaplacement, shear force and bending moment with pile diameter for three-row piles.

Fig. (8a-d). Variation of slope stability improvement factor (If), maximum pile diaplacement, shear force and bending moment with pile length for three-row piles.

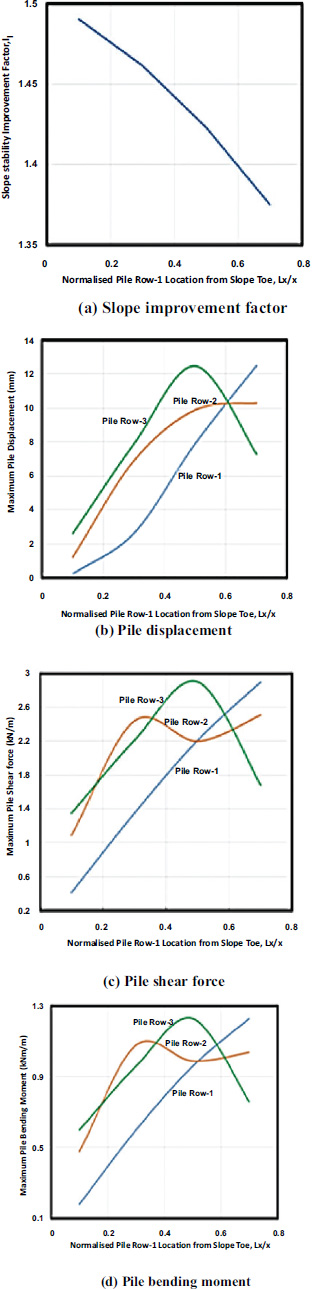
Fig. (10) illustrates the maximum pile displacement, shear force and bending moment increase with increasing pile location (L_x) for three-row small diameter steel piles in layered soil slope as shown in Fig. (1). However, for Pile Row-2 and Row-3, they increase up to the middle of the slope and then decrease thereafter. The depth of the failure surface at the pile location has a considerable effect on the soil-pile interaction and the mode of failure in pile-stabilized slopes. For the row of small diameter steel piles subjected to relatively shallow depths of sliding located close to the slope toe and crest, the dominant mechanism is flow of soil past the piles by rigid-body rotation without substantial flexural distortion and the group effects do not seem to play an important role. However, for the row of small diameter steel piles subjected to larger sliding depths located near the middle of the slope, the resistance developed by pile increases significantly when subjected to large sliding depth increases and the pile behaves as flexible and group effects play an increasingly important role. The Pile Row-2 and Row-3 are subjected to more soil pressure resulting higher maximum pile displacement, shear force and bending moment than the Pile Row-1 due to arching mechanism.

Fig. (9a-c). Variation of slope stability improvement factor (If) with slope inclination

Fig. (10a-d). Variation of slope stability improvement factor (If), maximum pile diaplacement, shear force and bending moment with pile length for three-row piles in layered soil slope