All published articles of this journal are available on ScienceDirect.
Component-level Performance-based Seismic Assessment and Design Approach for Concrete Moment Frames
Abstract
To solve the conservatism of acceptance criteria in ASCE/SEI 41 provisions, a new concept of component performance is put forward and an alternative method based on the statistical distribution of component performance levels to evaluate structural performance level is proposed. Independent component performance levels are redefined in detail and component performance indicator limits are developed, which are different from acceptance criteria for integral target performance level of entire building proposed by ASCE standards. Structural components are classified into critical components and general components. The relationship between structural performance levels and the statistical distribution of component performance levels, including performance levels of critical components, general components and non-structural components, is proposed. A framework for applying this method will be discussed in detailand implemented to a seven-story moment frame. It is concluded that this new evaluation method is simple and meaningful for performance-based seismic assessment and design.
1. Introduction
1.1. Development of Performance-Based Seismic Assessment and Design (PBSAD)
Since the 1990s, performance-based seismic engineering concepts and approaches have been developed by a series of documents including SEAOC version 2000 Report [1], ATC 40 Report [2], FEMA 273 Report [3] and its companion documents the FEMA 274 [4], FEMA 356 Report [5], FEMA 343 Report [6], ASCE/SEI 31-03 standard [7], ASCE/SEI 41-06 standard [8] and its Supplement 1 [9], and the latest Edition of ASCE/SEI 41 [10] published in 2013 and many other important reports. These documents 1) outlined the initial concept of performance levels related to vulnerability and varied levels of seismic hazard; 2) introduced the concept of performance in terms of discretely defined performance levels with names intended to connote the expected level of damage: Collapse, Collapse Prevention, Life Safety, Immediate Occupancy, and Operational Performance, performance objectives were developed by linking one of these performance levels to a specific level of earthquake hazard; and 3) introduced the concept of performance related to damage of both structural and non-structural components. Acceptance criteria of structural performance levels for each type of structural components are basic datas for engineering aplications of these documents. One of most important steps of performance-based assessment procedures of RC buildings relies on comparison of deformations obtained from nonlinear structural analyses (static or dynamic) with deformation performance limits, or acceptance criteria on the other words. These deformation limits significantly affect the assessment result so their accuracy plays a critical role. Performance-based seismic assessment method has been constantly updated, before the next-generation performance-based seismic assessment method is proposed, each development of this method was based on the new engineering practice with the tendency to release the acceptance criteria because the acceptance criteria was considered very conservative in engineering practice.
In 2001, under the ATC-58 Project, ATC began working on the next-generation performance-based seismic design criteria for new and existing buildings. In 2003, Moehle and Deierlein [11] first published paper about the performance-based seismic engineering framework which was developed by the Pacific Earthquake Engineering Research Center (PEER). The PEER framework expresses earthquake performance in terms of the probable values of key performance measures, such as casualties, repair costs, and occupancy loss derived from an application of the total probability theorem. In 2006, T.Y. Yang et al. [12] developed an application of this framework that utilized a modified Monte Carlo approach to implement the integration using inferred statistical distributions of building response obtained from limited suites of analyses. The ATC project team ultimately adopted and expanded this approach into the FEMA P-58 methodology. In the same year, FEMA 445 Report [13] was published and acted as the guidelines for the next-generation procedures. The primary objective of the next-generation procedures focuses on these aspects of 1) how to communicate with stakeholders effectively; 2) procedures for estimating the probable repair costs, casualties, and time of occupancy interruption; 3) assessment of economic loss associated with damaging earthquakes; 4) investigation of the conservatism and reliability of present second-generation acceptance criteria and modification of performance assessment based on global response parameters, so that the response of individual components does not unnecessarily control the prediction of overall structural performance. In 2012, FEMA P-58 [14] was published as the final product of ATC-58 project, which uses a probabilistic approach to characterize performance so that the reliability with which performance may be attained can be fully understood. Rather than using discrete performance states like that used in ASCE/SEI 41 methodology, the FEMA P-58 methodology characterizes performance in the form of loss distributions, from which the probability of incurring earthquake impacts, exceeding various levels can be directly obtained.
1.2. Problems and Criticism
In the development of performance-based seimic engineering, there exists a fundamental problem about the conservatism of the acceptance criteria for each structural performance level (generally known as the deformation limits of deformation-controlled components), which may lead to excessive cost of strengthening and reconstruction, sometimes even incorrect performance evaluation results . G. Siahos and S. Dritsos [15] compared ASCE 41-06 Supplement 1, FEMA 356 and the Eurocode 8 based on Greek Retrofitting Code via pushover analyses for the seismic assessment of RC buildings designed to old codes and results showed all procedures overestimated the experimentally observed limited damage. B. Acun and H. Sucuoglu [16,17] tested 12 full-scale column specimens designed for pure flexure failure and proved that the deformation-based performance limits proposed for substandard columns by ASCE/SEI 41-06 were found very conservative in view of the test results, which may lead to misleading results in the seismic risk assessment of existing substandard concrete structures. P. Ricci [18] also tested older-type reinforced concrete columns with plan bars and observed a significant conservatism in the plastic deformation capacity model of ASCE/SEI 41 provisions and proved that deformation limits could be relaxed while still meeting code safety requirements.
Authors survey this conservatism from another point of view. Considering the basic performance level concept and the application procedures proposed by ASCE/SEI 41, it can be pointed that the target building performance level controls the acceptable structural performance level and further controls acceptance criteria of all structural components, in other words, performance levels of a building and its components are associated with each other, thus not independent from each other. However, it is unreasonable to judge that a building or structure fails to meet the target performance level if only one component fails to meet the acceptance criterion. On the other hand, releasing the acceptance criteria of components could not address the problem effectively and may lead to unsafe assessment results in some cases. J. Moehle and G.G. Deierlein [19] also criticized that it is one of shortcomings that the overall system performance is assumed to be equal to the worst performance calculated for any component in the building. FEMA 445 [13] also realized this problem and stated that one of the main goals of the next-generation performance-based seismic engineering is to investigate the conservatism and reliability of present acceptance criteria, and to modify current structural procedures to assess structural performance based more on global response parameters, so that the response of individual components does not unnecessarily control the prediction of overall structural performance. FEMA P-58 report is just the product of this target. Although FEMA P-58 method has been available for seismic assessment and design, however most designers are far unfamiliar to the concept of PBEE framework and the probability-based assessment method, then it is meaningfull for a simplified performance-based seismic assessment method that can be easily understood and applied, which is the main research object of this paper.
1.3. Framework of this Paper
From authors’ point of view, authors [20-26] have put forward a new concept of component performance levels (hereinafter referred to as CPLs, while CPL refers as its singular form) and redefined them based on the damage degree of component itself and developed basic deformation limits for RC members of moment frames for these CPLs of new concept, which are similar to the acceptance criteria of RC members in ASCE/SEI 41. If component performance was divided into several discrete CPLs and graded according to corresponding strutural performance level in ASCE/SEI 41, acceptance criteria in ASCE/SEI 41 can be considered as deformation limits for CPLs. The major difference between these two limits is whether the component performance level is dependent/independent on the corresponding structural performance level. Obviously, CPL’s defination of author’s research findings is independent, while that of ASCE/SEI 41 is dependent.
To evaluate the seismic performance of structure based on these component performance levels defined and achieved by authors, an alternative method has also been proposed in this paper by establishing a new relationship between one given target structural performance level and the statistical distribution of structural component performance levels. The non-structural component performance level shall also be considered in terms of establishing another relationship between one selected target structural performance level and the statistical distribution of non-structural component performance levels, which can refer to research results by Yang and Ou [27]. Finally, evaluation of one typical concrete moment frame with masonry infills has been illustrated as a case study.
2. Theory
2.1. Structural Performance Levels (Hereinafter Reffered to as SPLs, while SPL Refers as its Singular form) and Ranges in China and Their Limitations
In China, Code for seismic design of buildings (GB50011-2010)[28], and the Technical specification for concrete structures of tall building (JGJ3-2010)[29] and its local Edition of Guangdong province [30] has introduce the performance-based seismic design idea and put forward concept of structural performance levels related to vulnerability and varied levels of seismic hazard, similar to the ASCE standards but with more detailed discrete performance levels, including Integrity Level (S-1) , Minor Damage Level (S-2), Limited Moderate Damage Level (S-3), Moderate Damage Level (S-4), Limited Serious Damage Level (S-5), Serious Damage Level (S-6) and Unacceptable Level (S-7). Compared descriptions of damage for each performance levels defined by Chinese Codes to those by ASCE Standards, S-1 is similar to Operational Performance Level, S-2 similar to Immediate Occupancy Level, S-4 similar to Life Safety Level, S-6 similar to Collapse Prevention Level and S-7 similar to Collapse Level. Although there are still some differences between each pair of similar performance levels, it can help understand definitions of structural performance levels in Chinese Codes for researchers outside Mainland China as well as structural performance levels referred to Chinese codes in context.
Chinese Codes suggest a force-based design method which adopts load combination equation with different combination coefficients to represent the acceptable damage degree of each performance level, and recommends the limited elasto-plastic interstory drift ratio as macro-measurement for additional performance level indicator. From authors’ previous research, the elasto-plastic interstory drift ratio of a structure can reflect whether the deformation capacity is able to meet the functional requirement, but it cannot reflect damage distribution of components. The force-based design method lacks for knowledge about damage levels of components and for information of either displacement ductility or rotation ductility of components. Because the extent of damage is proportional to plastic deformation, it is the deformation demand rather than the force demand of components and/or elements and/or structures that should be taken as the basic indicator to the performance levels. Therefore, although Chinese Codes have adopted concepts of performance-based seismic engineering, they have not adopted an appropriate approach for performance-based seismic assessment.
Based on the analysis above, this paper will take the concepts of structural performance levels and ranges defined by Chinese Codes, and complement new concepts of component performance levels and ranges and their deformation performance limits, then put forward new acceptance criteria for structural perfomance assessment procedures.
2.2. Structural Component Performance Levels (CPLs) and Ranges
All components actions shall be classified as either deformation controlled or force controlled based on their ductility. If the ductility is less than 2, the action shall be classified as a force-controlled action, otherwise it shall be classified as a deformation-controlled action. In general, for common framing systems, shear, axial force and torsion shall be considered as force-controlled actions, while moment may be either deformation-controlled or force-controlled action. Similarly, components shall also be classified as either deformation controlled or force controlled. If the failure of a component is controlled by a force-controlled action, the component shall be classified as a force-controlled component; otherwise if the failure is controlled by a deformation-controlled action, it shall be classified as a deformation-controlled component.
As mentioned above, CPLs of deformation-controlled componets have been divided into a range of seven discrete levels, including Integrity Level (C-1), Minor Damage Level (C-2), Limited Moderate Damage Level (C-3), Moderate Damage Level (C-4), Limited Serious Damage Level (C-5), Serious Damage Level (C-6) and Failure Level (C-7). Their definitions and descriptions are listed in detail as follows, which are modified from previous researches those can be found in references [23-25].
Integrity Level (C-1), is defined as a post-damage state in which no apparent or visible damage occurs. Component remains its pre-damage strength and stiffness. In a broad sense, component is still in elastic state. However, minor cracks on concrete cover may be permitted but tensile longitudinal reinforcement should not yield. The maximum compression strain of concrete could not exceed 0.002, and the maximum tensile strain of steel could not exceed fy/Es, where fy and Es are the yield strength and the Young's modulus of steel respectively. The limited deformation is referred as the yield deformation Δy (in displacement) or θy (in rotation).
Minor Damage Level (C-2), is defined as a post-damage state in which some visible but slight damage occurs, component yields, the stiffness decreases while the strength has not reached the strength capacity. The edge of concrete cover has been crushed but the maximum width of residual cracks is less than 1mm. The maximum compression strain of concrete could not exceed 0.004, and the maximum tensile strain of steel could not exceed 0.015.
Limited Moderate Damage Level (C-3), is defined as a continuous range of post-damage state between the Moderate Damage Level (C-4) and the Minor Damage Level (C-2). The concrete cover has not fallen off, concrete core remains integrity and the maximum width of residual cracks shall be less than 2mm. The maximum compression strain of concrete could not exceed 0.0065, and the maximum tensile strain of steel could not exceed 0.030.
Moderate Damage Level (C-4), is defined as a post-damage state in which the strength has reached its capacity and maybe exhibited less than 5% decrease compared to the peak strength. Buckling or fracture of longitudinal reinforcing bars does not occur, and the concrete does not crush. The maximum compression strain of concrete could not exceed the ultimate compressive strain, marked as εcu in context, and the maximum tensile strain of steel could not exceed 0.050 and 0.6εsu, where εsu is the ultimate tensile strain of steel.
Limited Serious Damage Level (C-5), is also defined as a continuous range of post-damage state between the Moderate Damage Level (C-4) and the Serious Damage Level (C-6). The strength may have less than 10% drop from the peak strength. The maximum tensile strain of steel could not exceed 0.080 and 0.9εsu.
Serious Damage Level (C-6), is defined as a post-damage state in which component is near failure. Buckling or fracture of longitudinal reinforcement may occur and the concrete core may crush with hoops failure. The maximum tensile strain of steel could not exceed 0.100 and εsu. The ultimate deformation (Δuin displacement, or θuin rotation) shall be reached when component has a serious strength 20% drop from the peak strength.
Failure Level (C-7), is defined as a post-damage state that the component has failed. For deformation-controlled components, a residual strength that equals to 20% of the yield strength could be considered for numerical analysis.
For force-controlled components, there are only two component performance ranges:the Integrity Level (C-1) and the Failure Level (C-7). In the Failure Level (C-7) of the force-controlled components, the residual strength should be set as zero for numerical analysis, and the peak strength should be taken as the threshold indicator from the Integrity Level (C-1).
In previous research, the elasto-plastic rotation angle is selected as the deformation indicator. The elasto-plastic rotation angle is the rotation over the plastic hinging region at the end of the member. if member is under inelastic response, the elasto-plastic rotation consists the elastic rotation angle and the plastic rotation angle; if member is not yield, the elastio-plastic rotation angle only consists the part of elastic rotation angle. In any case, the elasto-plastic rotation angle is the total rotation of the end lateral section of the plastic hinging region. Deformation-controlled CPLs those meet latest updated required constructional details of Chinese Codes published from 2010, have been developed and listed in Table 1 for RC columns and Table 2 for RC beams, whose earlier editions could be found in references [23-25]. It shall be noted for values and special symbols appears in these tables that 1) values in each table refer to the elasto-plastic rotation angle; 2) values between those listed in each table should be determined by linear interpolation; 3) nt is the axial compression ratio, which equals to the design axial force P divided by the gross sectional area Ag and concrete compressive strength fc, where fc is in MPa units, nt=P/(Agfc); 4). m is the flexure shear ratio, which equals to the flexure strength of member Mu, caculated based on the actual reinforcement and concrete strength, divided by the shear strength V0 and the nominal shear span ratio λ and the effective height of section h0 , m= Mu/(λh0V0),; 5). v is normal shear stress ratio, which equals to the design shear force V divided by the gross sectional area Ag and the tensile strength of concrete ft , where ft is in MPa units, v= V/( Agft).
Limits for CPLs of RC columns controlled by deformation.
| CPLs | C-1 | C-2 | C-3 | C-4 | C-5 | C-6 | |
|---|---|---|---|---|---|---|---|
| i. Flexure Failure | |||||||
| nt | m | ||||||
| ≤ 0.1 | ≤ 0.4 | 0.004 | 0.015 | 0.025 | 0.035 | 0.045 | 0.050 |
| ≤ 0.1 | ≥ 0.6 | 0.004 | 0.010 | 0.020 | 0.030 | 0.035 | 0.040 |
| ≥ 0.6 | ≤ 0.4 | 0.004 | 0.008 | 0.012 | 0.015 | 0.020 | 0.025 |
| ≥ 0.6 | ≥ 0.6 | 0.004 | 0.006 | 0.010 | 0.012 | 0.015 | 0.020 |
| ii. Flexure-Shear Failure | |||||||
| nt | m | ||||||
| ≤ 0.1 | ≤ 0.4 | 0.003 | 0.013 | 0.018 | 0.028 | 0.038 | 0.043 |
| ≤ 0.1 | ≥ 0.6 | 0.003 | 0.008 | 0.011 | 0.023 | 0.028 | 0.033 |
| ≥ 0.6 | ≤ 0.4 | 0.003 | 0.006 | 0.009 | 0.011 | 0.018 | 0.023 |
| ≥ 0.6 | ≥ 0.6 | 0.003 | 0.005 | 0.008 | 0.010 | 0.013 | 0.018 |
Limits for CPLs of RC beams controlled by deformation.
| CPLs | C-1 | C-2 | C-3 | C-4 | C-5 | C-6 | |
|---|---|---|---|---|---|---|---|
| i. Flexure Failure and Flexure-Shear Failure | |||||||
| m | v | ||||||
| ≤ 0.5 | ≤ 0.35 | 0.003 | 0.013 | 0.018 | 0.023 | 0.028 | 0.053 |
| ≤ 0.5 | ≥ 0.70 | 0.003 | 0.008 | 0.013 | 0.018 | 0.023 | 0.043 |
| ≥ 0.8 | ≤ 0.35 | 0.003 | 0.008 | 0.013 | 0.018 | 0.023 | 0.033 |
| ≥ 0.8 | ≥ 0.70 | 0.003 | 0.006 | 0.008 | 0.013 | 0.018 | 0.023 |
2.3. Structure Seismic Performance Criteria
2.3.1. General
A building performance level (hereinafter referred to as BPL, while BPLs refers as its plural form) is an estimation of comprehensive property, insured loss and the resistance capacity to a given seismic hazard level of certain intensity and certain probability, considering the anticipated structural damage, non-structural damage, equipment damage, occupancy interruption and any other loss of stakeholders. Due to massive types of losses, it is very difficult to proceed a comprehensive assessment of a building by one simple evaluation method. In this paper, the direct loss evaluation is the sole focus for a given structure. In this case, if considering the direct loss only, BPL and the structural performance level (hereinafter referred to as SPL, while SPLs refers as its plural form ) are equivalent. Since CPLs and their criteria are available, the next step is to consider the relationship between SPLs and CPLs. On the other hand, the non-structural components’ loss is also part of the total damage loss of a structure, so acceptance criteria for relationships between SPLs and non-structural components performance levels (hereinafter referred to as NPLs, while NPL refers as its singular form) need to be considered as well. Definitions and indicator limits of non-structural component performance ranges and levels have been achieved by Yang and Ou [27], which will be one basis of this study.
2.3.2. Simplified Acceptance Criteria of SPLs
No.177 Bulletin published by Ministry of Construction of China in 1990, Division standard for earthquake damage levels of building [31] and section 3.10 of the commentary to GB 50011, Code for seismic design of building [28] present a description of relationships between seismic performance levels and components damage as shown in (Table 3).
Acceptance criteria for each SPL has been translated from the corresponding relationship between SPLs and the damage distribution of structural/non-structural members given in Table 3, just as shown in Table 4 and Table 5 for structural components and the non-structural ones respectively.
Description of building performance levels.
| SPLs | Description | Remarks |
|---|---|---|
| Integrity (S-1) | structural members in good condition; individual non-structural members in slight damage. | Individual, means less than 5%; Some, means less than 30%; Most, means more than 50%. |
| Minor damage (S-2) | individual structural members have slight cracks; individual non-Structural members in obvious damage. | |
| Limited Moderate Damage (S-3) | some structural members in slight moderate damage; individual structural member in moderate damage; some non-structural members in obvious damage. | |
| Moderate Damage (S-4) | most structural members have minor cracks; some in obvious damage; individual non-structural members in serious damage. | |
| Limited Serious damage (S-5) | some structural members in not seriously damaged, individual structural member in severely damaged; some non-structural elements in serious damage. |
Acceptance criteria of SPLs with the statistical distribution of CPLs.
| CPLs SPLs |
C-1 | C-2 | C-3 | C-4 | C-5 | C-6 | C-7 |
|---|---|---|---|---|---|---|---|
| S-1 | — | 5% | 0% | 0% | 0% | 0% | 0% |
| S-2 | — | 30% | 5% | 0% | 0% | 0% | 0% |
| S-3 | — | 50% | 30% | 5% | 0% | 0% | 0% |
| S-4 | — | — | 50% | 30% | 5% | 0% | 0% |
| S-5 | — | — | — | 50% | 30% | 5% | 0% |
| S-6 | — | — | — | — | 50% | 30% | 5% |
Each row of Table 4 and Table 5 shows acceptance criteria for a related SPL in the first cell of the row. The value of each cell of a given SPL row means the limited statistical percentage of damaged components that exceed the CPL of the former column of this cell. If the content of a cell is “—”, it means that, to meet the corresponding SPL of the same row, there is no limitation about the statistical percentage of damaged components that exceed the CPL of the former column of this cell. If the statistical distribution of CPLs could not meet any SPL listed in each table, SPL of the structure should be considered as S-7.
Acceptance criteria of SPLs with the statistical distribution of NPLs.
| NPLS SPLs |
N-1 | N-2 | N-3 | N-4 | N-5 | N-6 | N-7 |
|---|---|---|---|---|---|---|---|
| S-1 | — | 30% | 5% | 0% | 0% | 0% | 0% |
| S-2 | — | 50% | 30% | 5% | 0% | 0% | 0% |
| S-3 | — | — | 50% | 30% | 5% | 0% | 0% |
| S-4 | — | — | — | 50% | 30% | 5% | 0% |
| S-5 | — | — | — | — | 50% | 30% | 5% |
| S-6 | — | — | — | — | — | 50% | 30% |
Obviously, if a structure’s performance meets a SPL of a “row”, it also meets the lower one. However, it’s prescribed that if the statistical distribution of CPLs of components in a structure meets all the requirements of a lower “row” but does not meet those of the upper one, SPL referring to the lower “row” should be selected as the structural performance level. For instance, when only considering the structural components, assuming that the structure under a given earthquake hazard level, the proportion of components that exceed C-2 is less than 50%, that exceed C-3 is less than 30%, that exceed C-4 is less than 5%, and no component beyond C-5 state, then the structural performance meets the SPL of S-4. Obviously it also meets the SPL of S-5 in the lower row, but does not meet the SPL of S-3 in the upper row, so only S-4 should be selected as the structural performance level. It is similar to the acceptance criteria for structural performance level with the statistical distribution of NPLs as shown in (Table 5).
In general, it is normal to draw two different SPLs when respectively considering structural members and non-structural members. Engineers are suggested to evaluate SPL by their profession and engineering experience according to specific circumstances and take responsibility for their given result. For example, when critical structural members are seriously damaged, structural component performance controls the SPL of structure. On the contrary, if critical structure components were in good condition or minor damaged but non-structural members are seriously damaged, considering economic losses or occupancy interruption, losses may be extremely high, then non-structural component performance controls the SPL of structure. This emphasizes the importance of the engineer's judgment, however, it’s appropriate in most cases to take the worst assessment result of structural componets and non-structural components as the performance level of structure, which shall be called “General Principle”. Discussions above present an alternative method of acceptance criteria for performance-based seismic assessment procedures. Limited values in Table 4 and Table 5 might be necessary to be modified for each type of structures according to engineering experience, but deformation limits for CPLs or NPLs would not be modified frequently as ASCE/SEI 41 does.
Because non-structural component performance levels could not be achieved directly from simulation analysis at present, the relationship between SPL and the statistic distribution of NPLs shall be only applied in post-damage evaluation procedures of existing buildings. However, in the following examples of performance evaluation of a new building, non-structural components are simulated by the technique of diagonal struts as per ASCE 41 guidelines to consider the contribution of stiffness and strength to structure, thus NPLs could be achieved from the deformation of struts, this relationship will also be taken into account. The drawback of technique of diagonal struts may lead to some confusions in the result, but it could be addressed by an improved method in future.
2.3.3. Modified Acceptance Criteria of SPLs by Distinguishing Components of Different Importance
Because different components contribute differently to structural performance, it is necessary to distinguish critical components and general components, which are similar to the primary components and secondary components defined in ASCE/SEI 41[8-10], however, they are defined and applied differently. ASCE/SEI 41 defines a primary component as a structural component that is required to resist seismic forces and accommodate deformations for the structure to achieve the selected performance level, and defines a secondary component as a structural component that accommodates seismic deformations and is not required to resist seismic forces for the structure to achieve the selected performance level, and it must be emphasized that the latest ASCE/SEI 41[10] applies the concept to distinguish primary and secondary components only in linear assessment procedures, in which primary components get more strict m-factors than secondary ones to achieve much higher reliability, and assumes that all structural components make their contribution to structural performance in the process of nonlinear analysis in nonlinear assessment procedures and reflect their different influence in analysis result.
Different from ASCE/SEI 41, this paper defines that: 1) a structural component that makes significant contribution to the lateral stiffness and the lateral resistance forces (or lateral strength) of the structure shall be classified as critical, i.e., if one component’s yield or failure leads to obvious alteration of distribution of the structural stiffness and resistance force, the component shall be categorized as a critical component, and 2) a structural component that could not be classified as a critical component, shall be categorized as a general one. Failure of general components may obviously affect the local structural performance, not the entire system performance.
Obviously, CPLs of critical components make more important effects on the overall structural performance than those of general ones, thus more strict acceptance criteria shown in Table 6 are applied for critical components. However, acceptance criteria shown in Table 4 shall be applied for general components.
Acceptance criteria of SPLs with the statistical distribution of CPLs for critical components.
| CPLs SPLs |
C-1 | C-2 | C-3 | C-4 | C-5 | C-6 | C-7 |
|---|---|---|---|---|---|---|---|
| S-1 | — | 0% | 0% | 0% | 0% | 0% | 0% |
| S-2 | — | 5% | 0% | 0% | 0% | 0% | 0% |
| S-3 | — | 30% | 5% | 0% | 0% | 0% | 0% |
| S-4 | — | 50% | 30% | 5% | 0% | 0% | 0% |
| S-5 | — | — | 50% | 30% | 5% | 0% | 0% |
| S-6 | — | — | — | 50% | 30% | 5% | 0% |
Observation of Table 6 shows that if a structure achieves one target performance level, any critical components exceeding the corresponding level of component’s performance are unacceptable. For example, if S-3 is selected as the target structural performance level, there shall be none critical components exceed the CPL of C-3, furthermore the proportion of components that exceed C-2 shall be less than 5% and that exceed C-1 shall be less than 30%. However, for general components, these requirements are relatively relaxed but also with many varied detailed requirements about proportions of components exceeding any component performance level. It is different from ASCE/SEI 41 provisions which require all structural components meet the same acceptance criteria for a target structural performance level.
2.4. Component-level Performance-based Seismic Assessment Procedures
There are three key challenges for performance-based seismic assessment procedures:1) reliable elasto-plastic analysis result, 2) appropriate performance indicators, and 3) reasonable acceptance criteria for each SPL. For component-level performance-based seismic assessment procedures, deformation and force are selected as indicators for deformation-controlled components and force-controlled components respectively. Acceptance criteria of SPLs mentioned above are selected. Procedures should be conducted as the follow chart shown in Fig. (1), considering structural components and non-structural components (if modeled) in a reliable elasto-plastic analysis process.
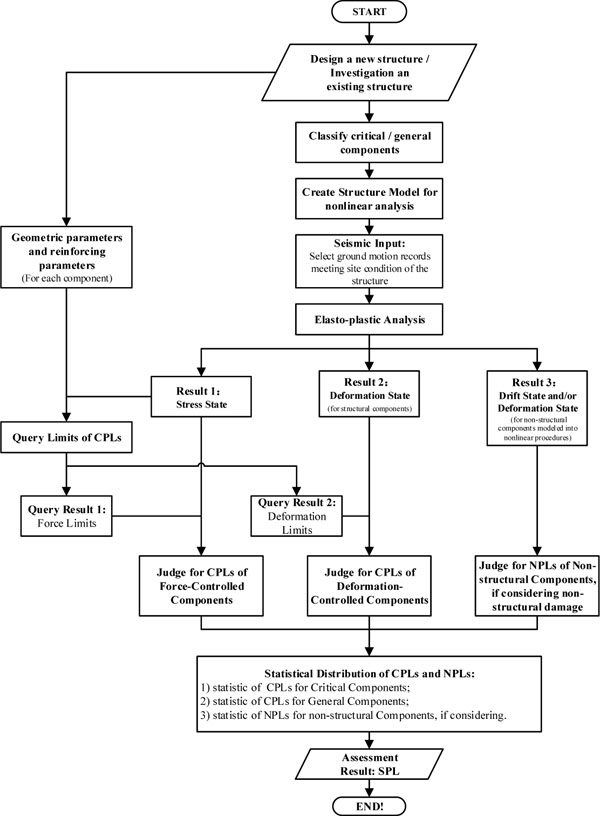
Component-level performance-based seismic assessment procedures.
- For a given structure of a new building or an existing building, the first step is to obtain the structural layout, dimensions and materials. For a new building, there should be design documents; and for an existing building, more as-built information about the structure is necessary and must be investigated in detail, with source design documents as reference. As a result of this step, geometry parameter, cross-section reinforcement and necessary material strength of each member will be determined.
- Classify structural components into critical components and general components. It will mainly depend on the expertise and experience of engineers.
- Build the elasto-plastic analysis model for the structure. For an existing building, analysis should reflect the actual material strength, effective member stiffness, effective vertical/horizontal resistance systems, and accurate joint connections. For a new building, analysis model should reflect design details.
- Select ground motion records those meet the site condition and the seismic hazard level of a given probability. Generally, no less than 3 records are needed for a comprehensive performance-based seismic assessment, performance evaluation should be conducted based on each selected record. Thus each performance assessment result is a certain analysis based on a given ground motion record, which just reflects one probable performance capacity of the structure.
- For one selected ground motion record from step 4), the elasto-plastic dynamic analysis should be conducted to obtain three types of results. Result 1 includes the stress state of all members along elasto-plastic dynamic analysis history, Result 2 includes the deformation state for structural components, and Result 3 includes the drift state of stories at macro scale and/or deformation state of non-structural components if non-structural components are modeled. It’s noted that drift state of stories shall be used to estimate NPLs if non-structural components are not modeled.
- Judge the action type of each member such as moment, shear, axial force, based on the geometry parameter, the cross-section reinforcement and the necessary material strength from step 1) and the stress state from step 5). If the member is deformation-controlled, then query deformation limits for each CPL of the member, whereas the normal strength or force limits shall be calculated or checked for force-controlled members. Performance indicator limits for non-structural components shall also be determined from research results of Yang and Ou [27].
- Based on results of deformation limits, force limits and/or non-structural component performance indicator limits from step 6), and results of deformation state and stress state outputted from step 5), the CPL and/or NPL of component shall be determined.
- Formulate statistic distribution of CPLs and/or NPLs separately, then evaluate performance level of the structure for the given ground motion record by acceptance criteria recommended in Table 4, Table 5 and Table 6.
- For another ground motion records of a seismic hazard level of same or different probability, repeat 2) to 8).
Seismic risk analysis for this method is not adopted in these procedures. It shall be taken account for more detailed evaluation procedures. However, this paper mainly deals with the evaluation method for one given seismic intensity of a certain and asuming equal probability.
3. Examples
One 7-storey moment frame that meets the minimum performance requirements of Chinese design specifications has been selected as an example with conditions of site-class II, degree 8 of seismic intensity (the peak acceleration is 0.2g). The structural layout is shown in Fig. (2), each floor height is 3600 mm, the concrete strength fc,beam=20.1MPa for beams and fc,column=23.4Mpa for columns, section of beams is 200x500 mm2 and that of columns is 400x400 mm2. Seven strong ground motion records are selected for the elasto-plastic analysis, marked as GM1 to GM7, whose response spectra are drawn in Fig. (3) with the design response spectrum, and the peak acceleration of all the records has been set to 0.2g in proportion. It should be noted that five records, GM1 to GM5 listed in Table 7, are real ground motion records at different seismic stations while another two records, GM6 and GM7, are artificial synthetic seismic ground motion records based on site conditions. P. Haldar [32] has modeled unreinforced masonary infills as diagonal struts as per ASCE/SEI 41 guidelines and compared the seismic vulnerability of bare and infilled frames. Simillar to P. Haldar’s work , this paper also modeled the structure into two different nonlinear analysis models on Perform-3D Software by simulating infill masonry walls as dead loads and as diagonal struts, which are marked as MF1 (Moment Frame 1) and MF2 (Moment Frame 2) respectively. In order to simplify this evaluation process, it is assumed that all vertical structural components are classified as critical components, and all horizontal ones classified as general components. In the model of MF2, diagonal struts shall be considered as non-structural components.
Acceptance criteria of SPLs with the statistical distribution of CPLs for critical components.
| ID | Magnitude | Site | Station |
|---|---|---|---|
| GM1 | 6.53 | Imperial Valley-06 | Callipatria Fire station |
| GM2 | 6.53 | Imperial Valley-06 | El Centro Array#8 |
| GM3 | 6.53 | Imperial Valley-06 | Niland Fire Station |
| GM4 | 6.53 | Imperial Valley-06 | Parachute Test Site |
| GM5 | 6.61 | San Fernando | LA-HollywoodStor FF |
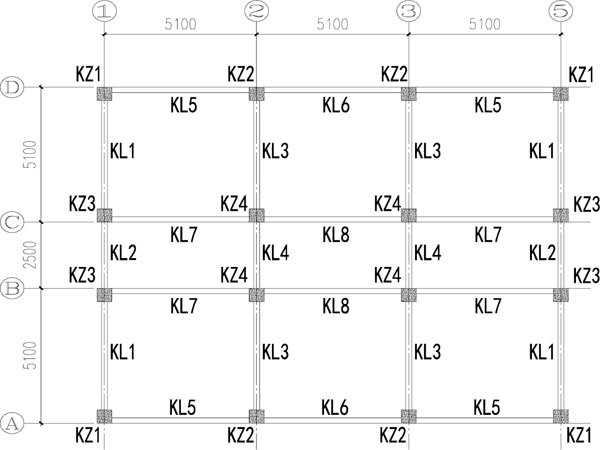
Structural layout.
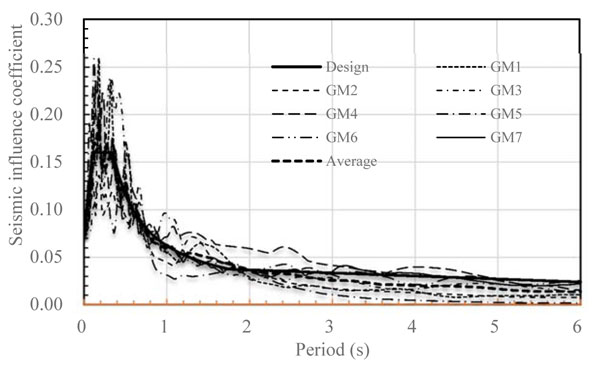
Response spectra of selected ground motions and the design/standard response spectrum.
3.1. Seismic Evaluation of Moment frame with Infill Masonry Walls Modeled as Dead Loads, MF1
The elasto-plastic analysis of MF1 has been conducted and statistic distributions of CPLs of general components and critical components are presented in Table 8 and Table 9 respectively. The last column of each table shows the assessment result for each seismic record just considering the listed statistics. Because infill masonry walls are considered as dead loads in the analysis model, so non-structural components’ influence on the structural performance level will not be considerd. Table 10 shows the comprehensive evaluation of MF1.
Statistic distribution of general components’ CPLs(%).
| General Components | SPL | |||||||
|---|---|---|---|---|---|---|---|---|
| C-1 | C-2 | C-3 | C-4 | C-5 | C-6 | C-7 | ||
| GM1 | -- | 57.1 | 38.1 | 0 | 0 | 0 | 0 | S-4 |
| GM2 | -- | 45.2 | 4.76 | 0 | 0 | 0 | 0 | S-3 |
| GM3 | -- | 57.1 | 11.9 | 0 | 0 | 0 | 0 | S-4 |
| GM4 | -- | 66.7 | 47.6 | 42.8 | 4.76 | 0 | 0 | S-5 |
| GM5 | -- | 57.1 | 26.2 | 0 | 0 | 0 | 0 | S-4 |
| GM6 | -- | 66.7 | 16.7 | 0 | 0 | 0 | 0 | S-4 |
| GM7 | -- | 61.9 | 28.6 | 0 | 0 | 0 | 0 | S-4 |
Statistic distribution of critical components’ CPLs(%).
| Critical Components | SPL | |||||||
|---|---|---|---|---|---|---|---|---|
| C-1 | C-2 | C-3 | C-4 | C-5 | C-6 | C-7 | ||
| GM1 | -- | 14.3 | 0 | 0 | 0 | 0 | 0 | S-3 |
| GM2 | -- | 0 | 0 | 0 | 0 | 0 | 0 | S-1 |
| GM3 | -- | 1.02 | 0 | 0 | 0 | 0 | 0 | S-2 |
| GM4 | -- | 13.3 | 8.16 | 0 | 0 | 0 | 0 | S-4 |
| GM5 | -- | 8.16 | 0 | 0 | 0 | 0 | 0 | S-3 |
| GM6 | -- | 8.93 | 0 | 0 | 0 | 0 | 0 | S-3 |
| GM7 | -- | 14.3 | 0 | 0 | 0 | 0 | 0 | S-3 |
Table 8 shows that, the damage distribution of general components meets SPL of S-4 under five ground motion records, and meets SPL of S-3 and S-5 under the other two ground motion records respectively. Table 9 shows that there are four ground motion records under which the damage distribution of critical components meets SPL of S-3, one ground motion record that meets SPL of S-1 without any critical components damaged, one ground motion record that meets SPL of S-2 with only few critical components damaged, and the last ground motion record that meets much lower SPL of S-4. For entire structure, the lower SPL due to critical and general components should be selected as the structure’s SPL, as listed in the last column of (Table 10). Because most records meet SPL of S-4, and only one meets much more serious damage level S-5, it can be concluded that the structure of MF1 shall achieve a performance level not lower than SPL of S-4 with a probability of no less than 85%. If different damages of beams (referring to general components) and columns (referring to critical components) are both considered, beams seem to be much more seriously damaged than columns, so that the design target of “strong column and week beam” is achieved.
Comprehensive evaluation.
| SPL | SPL of Structure | ||
|---|---|---|---|
| General | Critical | ||
| GM1 | S-4 | S-3 | S-4 |
| GM2 | S-3 | S-1 | S-3 |
| GM3 | S-4 | S-2 | S-4 |
| GM4 | S-5 | S-4 | S-5 |
| GM5 | S-4 | S-3 | S-4 |
| GM6 | S-4 | S-3 | S-4 |
| GM7 | S-4 | S-3 | S-4 |
3.2. Seismic Evaluation of Moment Frame with Infill Masonry Walls Modeled as Diagonal Struts, MF2
The elasto-plastic analysis of MF2 has been conducted and statistic distributions of CPLs of general components and critical components are presented in Table 11 and Table 12 respectively, along with the statistic distribution of NPLs of non-structural components simulated as diagonal struts presented in (Table 13). Because infill masonry walls are considered as diagonal struts modeled, performance levels of non-structural components are assessed by the response of diagonal struts. Table 14 shows the comprehensive evaluation of this structure.
Statistic distribution of general components’ CPLs(%).
| General Components | SPL | |||||||
|---|---|---|---|---|---|---|---|---|
| C-1 | C-2 | C-3 | C-4 | C-5 | C-6 | C-7 | ||
| GM1 | -- | 0 | 0 | 0 | 0 | 0 | 0 | S-1 |
| GM2 | -- | 11.9 | 0 | 0 | 0 | 0 | 0 | S-3 |
| GM3 | -- | 9.5 | 0 | 0 | 0 | 0 | 0 | S-3 |
| GM4 | -- | 0 | 0 | 0 | 0 | 0 | 0 | S-1 |
| GM5 | -- | 0 | 0 | 0 | 0 | 0 | 0 | S-1 |
| GM6 | -- | 0 | 0 | 0 | 0 | 0 | 0 | S-1 |
| GM7 | -- | 28.6 | 0 | 0 | 0 | 0 | 0 | S-3 |
Statistic distribution of critical components’ CPLs(%).
| Critical Components | SPL | |||||||
|---|---|---|---|---|---|---|---|---|
| C-1 | C-2 | C-3 | C-4 | C-5 | C-6 | C-7 | ||
| GM1 | -- | 0 | 0 | 0 | 0 | 0 | 0 | S-1 |
| GM2 | -- | 0 | 0 | 0 | 0 | 0 | 0 | S-1 |
| GM3 | -- | 0 | 0 | 0 | 0 | 0 | 0 | S-1 |
| GM4 | -- | 0 | 0 | 0 | 0 | 0 | 0 | S-1 |
| GM5 | -- | 0 | 0 | 0 | 0 | 0 | 0 | S-1 |
| GM6 | -- | 0 | 0 | 0 | 0 | 0 | 0 | S-1 |
| GM7 | -- | 0 | 0 | 0 | 0 | 0 | 0 | S-1 |
Statistic distribution of NPLs(%).
| Non-structural Components | SPL | |||||||
|---|---|---|---|---|---|---|---|---|
| N-1 | N-2 | N-3 | N-4 | N-5 | N-6 | N-7 | ||
| GM1 | -- | 100 | 85.7 | 66.7 | 38.1 | 14.3 | 4.7 | S-5 |
| GM2 | -- | 100 | 85.7 | 57.1 | 57.1 | 28.6 | 9.5 | S-6 |
| GM3 | -- | 100 | 90.5 | 71.4 | 61.9 | 42.8 | 21.4 | S-6 |
| GM4 | -- | 95.2 | 85.7 | 71.4 | 57.1 | 30.4 | 4.7 | S-5 |
| GM5 | -- | 100 | 85.7 | 71.4 | 42.8 | 28.6 | 4.7 | S-5 |
| GM6 | -- | 100 | 85.7 | 71.4 | 57.1 | 42.8 | 14.3 | S-6 |
| GM7 | -- | 100 | 90.5 | 71.4 | 71.4 | 42.8 | 21.4 | S-6 |
Comprehensive evaluation.
| SPL | SPL of Structure | |||
|---|---|---|---|---|
| General | Critical | Non-structural | ||
| GM1 | S-1 | S-1 | S-5 | S-5 |
| GM2 | S-3 | S-1 | S-6 | S-6 |
| GM3 | S-3 | S-1 | S-6 | S-6 |
| GM4 | S-1 | S-1 | S-5 | S-5 |
| GM5 | S-1 | S-1 | S-5 | S-5 |
| GM6 | S-1 | S-1 | S-6 | S-6 |
| GM7 | S-3 | S-1 | S-6 | S-6 |
Table 11 shows that, there are four ground motion records under which the damage distribution of general components meets SPL of S-2 with no more than 30% of general components slightly damaged, all other records cause no damage to general components. Table 12 shows that, there is no damage to critical components under anyone of these seven ground motion records. On the contrary, Table 13 shows that non-structural components are damaged severely under all selected ground motion records. The damage distribution of non-structural components meets SPL of S-5 under three ground motion records and meets SPL of S-6 under other four records. Table 14 shows the comprehensive evaluation for entire structure, the lowest SPL shall be selected as the structure’s SPL, as listed in the last column of this table. Based on the judgment principle of SPL, S-6 shall be selected as the SPL of MF2 with no more than 15% probability of exceeding. In this case, structural components are damaged very slightly, while non-structural components are damaged seriously, it shall be predicted that this structure may cause a serious economic losses if it is luxuriously decorated.
Compared to the assessment result of MF1, it seems to be concluded that well infilled moment frames may lead to much more serious damage on the infill masonry walls instead of structural members. Although structural components are slightly damaged, economic loss due to the damage of non-structural components may be unacceptable. This is one of the major difference between performance-based seismic assessment procedures and traditional design approaches.
It is noteworthy that in the analysis model of MF2, all punches of doors and windows in the infill masonry walls are not considered, so stiffness and strength contributed by diagonal struts may be over-estimated, and the conservative definition of non-structural component performance levels by Yang and Ou [27] may also affected the outcome.
Conclusion and Future Research
- This paper presents a new method for performance-based seismic assessment based on statistic distribution of component damage. Different from the ASCE method, it gives a new sight that component performance levels are defined based on damage extent of components themselves, rather than defined based on acceptance criteria of target structural performance level. It also provides a possible approach to study the performance of components and structures and their relationship independently, which is meaningful for performance-based seismic research. Examples show that this new method could be easily applied and understood.
- Definition of Components’ performance levels are presented and performance indicator limits for members of moment frames have been achieved, which are mainly based on definitions of material strain limits for each component performance level. A simple relationship between the structural performance level and the statistic distribution of component performance levels has also been achieved, however more detailed work about the “relationship” needs to be conducted, which may include different importance of different members and their different effect on the structural performance level.
- For the lack of the non-structural component performance levels those are accommodative to this method, an in-depth and ongoing study on the non-structural components shall be further conducted.
However, this method may not be a complete seismic performance assessment method but it will give a new perspective for the PBSAD practice and make some meaningful effect.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
This work was financially supported by the National Natural Science Foundation of China (Grant No. 51378221 ) and State Key Laboratory of Subtropical Building Science Foundation (Grant No. 2014ZC16).


